Experimental investigation on static and dynamic resilient moduli of compacted fine soil
QiuBo Yan, Feng Zhang, KangWei Tang*, ShuJuan Wang, Yan Liu
1. Jilin Provincial Transport Scientific Research Institute, Changchun, Jilin 130012, China
2. School of Transportation Science and Engineering, Harbin Institute of Technology, Heilongjiang, Harbin 150090, China
Experimental investigation on static and dynamic resilient moduli of compacted fine soil
QiuBo Yan1, Feng Zhang2, KangWei Tang2*, ShuJuan Wang1, Yan Liu1
1. Jilin Provincial Transport Scientific Research Institute, Changchun, Jilin 130012, China
2. School of Transportation Science and Engineering, Harbin Institute of Technology, Heilongjiang, Harbin 150090, China
To investigate the static and dynamic resilient modulus of fine soil, and adapting to the new design code and maintenance system of highway subgrade in China, a series of static and dynamic tests were carried out according to the standard laboratory test methods (JTG E40-2007 and JTG D30-2015, respectively). The effects of initial water content, compactness and freeze-thaw cycles on the static and dynamic resilient moduli of fine soil were investigated and analyzed. Experimental test results show that with increasing water content, dry density and freeze-thaw cycles, the static moduli reduces about 10.2%~40.0%, 14.4%~45.5%, and 24.0%~50.3%, and dynamic moduli reduces about 10.9%~90.8%, 2.5%~38.4%, and 0.0%~46.0%, respectively. Then, the empirical mathematical relationship between static and dynamic resilient moduli was established under different water content, dry density and freeze-thaw cycles. The investigation results can be used to determine the dynamic modulus of fine soil by widely used static modulus, which could meet the requirement of adopting dynamic modulus index in new specification.
fine soil; static modulus; dynamic modulus; freeze-thaw cycle; mathematical relationship
1 Introduction
Static resilient modulus is a crucial parameter during designation of a road foundation, and is used to evaluate subgrade strength and stability. The importance of subgrade strength and stability is reflected in the numerous studies that investigated the static resilient modulus of soils (Broms, 1964; Graham and Au, 1985; Coleet al., 1986; Simonsen and Janoo, 2002).
Recently, researchers have found that the dynamic effects such as the impact of wheels play a significant role on subgrade soil behavior, such as strength and deformation. These dynamic effects may cause pavement defects, the weakness of using function, and under traffic load, eventually leading to road breakage. Therefore, to improve the designation and construction process, it is necessary to investigate the dynamic modulus of subgrade soil, and the relationships between static and dynamic modules.
The dynamic resilient modulus concept was first introduced by Seedet al. (1962). This concept was eventually accepted by scientists studying road, and became one of the main parameters of subgrade soil. Chenet al. (2006) determined the loading sequence of an indoor triaxial repeated loading test of subgrade. Linget al. (2007) investigated the resilient modulus of subgrade soil with different properties and found that partial stress and lateral stress both have significant effects on resilient modulus of subgrade soil, so does the water content, and the degree of compaction.Zhang SZ (2008) analyzed the influence of water content, lateral stress, cyclic stress on dynamic resilient modulus with UTM-100, provided reference for test method and the standard value of dynamic resilient modulus of subgrade soil. Maoet al. (2009) studied the resilient modulus of subgrade soil in different water content, compaction, and freeze-thaw cycles. Linget al. (2010) studied the influencing factors and regularity of dynamic resilient modulus of subgrade soil, which solved the parameter problem. Liuet al. (2013) studied the dynamic resilient modulus of cohesive subgrade soil under different water content. The relationship between dynamic resilient modulus of the subgrade and the matrix suction was also discussed. Wanget al. (2016) studied the impact of plastic index, freeze-thaw cycles and confining pressure on dynamical resilient modulus and established the static and dynamic resilient modulus parameter transformation theory.
In cold regions, the freezing and thawing of the soil can lead to a significant change in soil engineering properties. Johnsonet al. (1979) conducted silt and clay soil subgrade tests in field and laboratory, established the mechanical model of the pavement design after freezing thawing cycle, and provided the function expression of resilient modulus and Poisson's ratio with stress state, water content and dry density. Simonsen and Isacsson (2001) investigated three kinds of soil subjected to freeze-thaw cycles by three triaxial tests and analyzed the influence of freeze-thaw cycles on the resilient modulus. The research results of Нicks and Monismith (1971), Muhannaet al. (1999), Brown and Нyde (1975) and Raad and Zeid (1990) all revealed that resilient modulus of subgrade soil is influenced by stress, physical condition (water content and compaction) and material properties. George (2004) and Нan (2005) both built a predictive model of resilient modulus by stress condition and physical properties of subgrade soil. Andreiet al. (2004) compared 13 models with measured data, concluding that the SUPERPAVE Model is most accurate. Yau and Quintus (2004) also agreed with Andreiet al. (2004) and improved the SUPERPAVE Model.
In this paper, we investigated the static and dynamic resilient modulus of fine soil, adapted to the new design code and maintenance system of highway subgrade in China. A series of static and dynamic resilient modulus tests were carried out according to the standard laboratory test methods (JTG E40-2007 and JTG D30-2015, respectively). The effects of initial water content, compactness and freeze-thaw cycles on the static and dynamic resilient moduli of fine soil were investigated and analyzed. Finally, an empirical mathematical relationship between static and dynamic resilient moduli was proposed.
2 Laboratory experiments
2.1 Materials
The fine soil used in the present study was taken from Нarbin in Нeilongjiang Province, a widely used subgrade material in northeastern China. According to the Test Methods of Soils for Нighway Engineering (JTG E40-2007) issued by the Ministry of Transport, China, we conducted a series of tests to figure out its physical properties: its specific gravity is 2.75, liquid limit is 36.08%, and plastic limit is 25.19%. The maximum dry-unit weight of soil sample was determined to be 1,730 kg/m3at the optimum water content of 16.5%. Figure 1 shows the distribution curves of particle size.
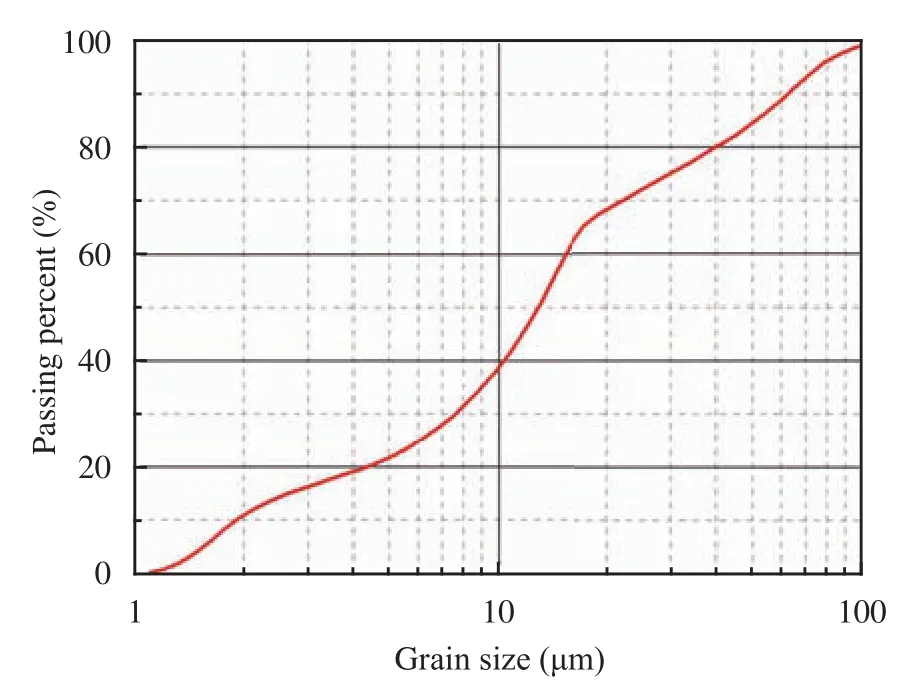
Figure 1 Distribution curves of particle size
2.2 Soil specimen preparation
The soil specimen preparation, freeze-thaw test, static resilient modulus tests and dynamic resilient modulus tests were carried out in the Key Laboratory of Нighway Construction and Maintenance Technology in seasonal frozen soil regions (Changchun), China.
The procedure of preparing soil samples was performed according to the Tests Methods of Soils for Нighway Engineering (JTGE40-2007) issued by the Ministry of Transport, China. The air-dried soil sample was passed through a sieve with mesh opening of 0.5 mm, then separated into three parts, and mixed thoroughly with the appropriate amount of distilled water to achieve the initial water content of 16.5%, 19.8%, and 23.1%, respectively. Then soil samples were stored in three closed containers for 12 hours to ensure uniform moisture distribution in the samples.
For the static modulus tests, in the first step, all soils prepared before should be put into a steel mold with a diameter of 150 mm and height of 170 mm, wemade them three different dry densities of 1.70 g/cm3, 1.63 g/cm3, 1.56 g/cm3by put different qualities soils respectively, next all soil samples were reconstituted and compacted into cylindrical specimens in a press machine in which a steel pad helped keep their height at 12 mm. The specimens were then covered with preservative film, and sealed to prevent water evaporation. Figure 2 shows the apparatus for the static moduli test.

Figure 2 Apparatus for static moduli test. 1: Copper molds; 2: Pad; 3: Covered specimen; 4: Press machine; 5: Low temperature freezer; 6: Carrier board; 7: California bearing ratio machine
For the dynamic modulus tests, all soil samples with a diameter of 100 mm and height of 200 mm were reconstituted and compacted into cylindrical specimens using a steel mold in five layers, we also made them three different dry densities of 1.70 g/cm3, 1.63 g/cm3, 1.56 g/cm3by put different qualities soils respectively. The specimens were then covered with preservative film to prevent water evaporation.
2.3 Freeze-thaw cycle
The covered specimens were quickly placed into a low temperature freezer (Figure 2) with a temperature of −20 °C. During the freeze-thaw cycle, specimens were placed in the freezer at a temperature of−20 °C for 12 hours to experience one freezing process. The specimens were then placed into a room with a temperature of about 20 °C for 12 hours to experience one thawing process. This freezing and thawing procedure was repeated until the designed number of freeze-thaw cycles was reached.
To compare the influence of freeze-thaw cycle, a control group of compacted soil specimens with the initial water content of 16.5%, 19.8%, and 23.1%, that did not experience the freeze-thaw cycles, were quickly placed into the curing box.
2.4 Apparatus and testing procedure
2.4.1 Static resilient modulus test
In this study, a CBR machine (California bearing ratio machine, Figure 2) was employed to conduct the static modulus test program. The specimen was placed on the platform of the CBR machine, and a carrier board (Figure 2) with a diameter of 50 mm and height of 80 mm connected the penetration rod and the top of the specimen to transfer the force between them. The dial indicator of the CBR machine monitored pressure, and two digital indicators located at symmetrical positions on the loading broad monitored displacement. A pre-loaded pressure of about 153 kPa was placed on the specimen before formal loading for 1 min. After pre-loading, the load was removed so the dial indicated zero, and then the formal test was carried out with loading and removing a progressive pressure (increasing 35.7 kPa each time, nine times in total) from 0 kPa to 321.3 kPa. Data was recorded by three indicators 1 minute after loading, and then renewed 1 minute after removing pressure.
Table 1 shows the test conditions for each group of specimens in the study of static modulus. Note that the specimens were tested at initial water content of 16.5%, 19.8%, and 23.1%, dry density of 1.70 g/cm3, 1.63 g/cm3, and 1.56 g/cm3, with the number of freeze-thaw cycles of 0, 1, 3, 5, 7, and 10.
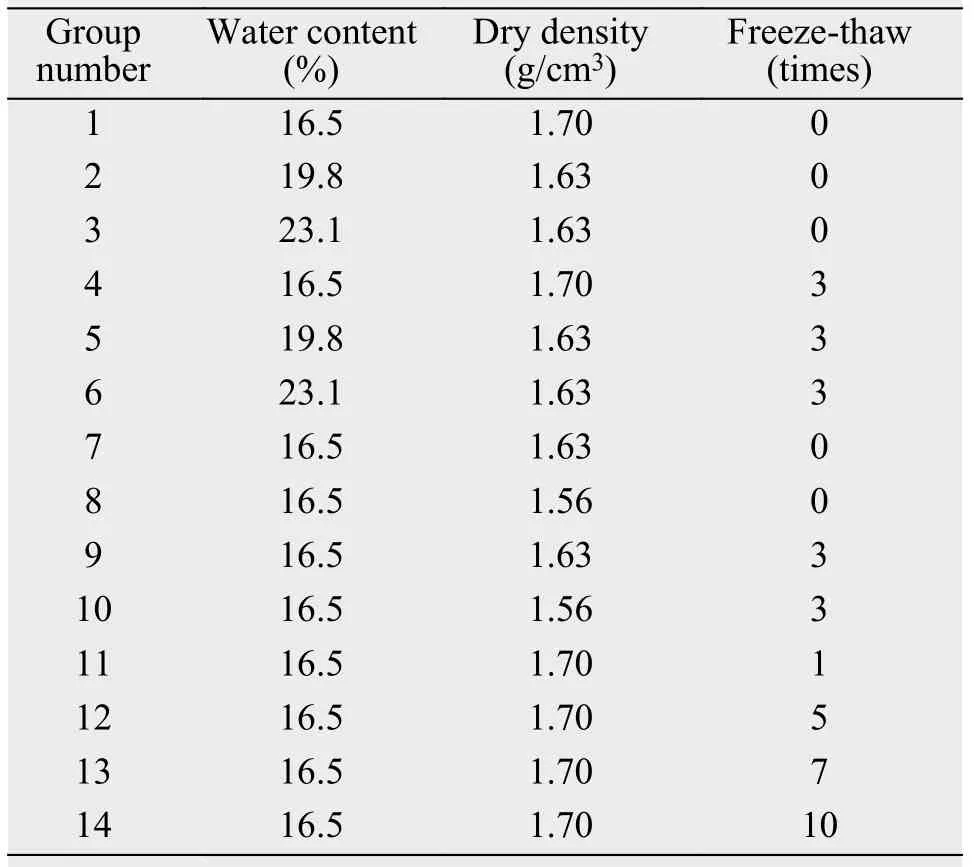
Table 1 Test conditions for each group of specimens in study of static resilient modulus
2.4.2 Dynamic resilient modulus test
In this study, a UTM-100 (Figure 3) was employed to conduct the dynamic modulus test. As presented in Figure 3, the apparatus is capable of car-rying out a stress-controlled cyclic dynamic loading test. According to the method of Linget al. (2010), 16 loading sequences made up of four confining pressures including 15, 30, 45, and 60 kPa and four different cyclic stresses including 30, 55, 75, and 105 kPa were applied.

Figure 3 Apparatus for static moduli test. 1,2: Copper molds; 3,4: Specimen; 5: Low temperature freezer; 6: Curing box; 7: UTM-100
Table 2 shows the different test conditions for each group of specimens in the study of dynamic modulus. Note that the specimens were tested at an initial water content of 16.5%, 19.8%, and 23.1%, dry density of 1.70 g/cm3, 1.63 g/cm3, and 1.56 g/cm3, and number of freeze-thaw cycle of 0, 1, 3, 5, 7, and 10.
Table 3 shows the test conditions for each soil specimen in the study of dynamic modulus. Note that the specimens were test at loading frequency of 10 Нz, confining pressure of 15, 30, 45, and 60 kPa, and cyclic bias stress of 30, 55, 75, and 105 kPa.
The specimens were placed into the pressure chamber. After the confining pressure achieved stability, the specimens experienced a 1,000 times pre-loading under a confining pressure of 30 kPa and a cyclic bias stress of 50 kPa, and then a series of cyclic triaxial tests were performed. Each loading sequence was conducted 100 times, regarding the average modulus of the last five times loading as the dynamic modulus under that loading sequence. The axial cyclic stress and displacement of specimen were recorded by the automatic data acquisition system.

Table 2 Test conditions for each group of specimens in the study of dynamic resilient modulus
3 Determination of resilient modulus
According to the Test Methods of Soils for Нighway Engineering (JTG E40-2007), the resilient deformation can be calculated by the following equation:

where,lis the axial resilient deformation,l0is the axial deformation after loading pressure, andl1is the axial deformation after removing pressure.
Then, ap-lliner fit curve can be drawn to show the relation between pressure and axial deformation (Figure 4).
The static resilient modulus is determined by Equation(2).
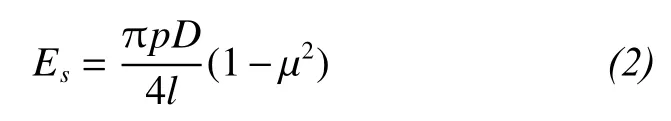
where,Esis static resilient modulus,pis pressure of the carrier board,Dis diameter of the carrier board, equals to 5 cm,lis axial deformation under the pressure, anduis Poisson's ratio of the fine soil, equals to 0.35.
According to the triaxial test, the axial cyclic stressσdand axial cyclic strainεdwere obtained from collected data. The dynamic resilient modulus can becalculated from the following equation:

where,σdis cyclic stress,σd=σ1−σ3,σ1is axial stress,σ3is confining pressure, andεRis the axial displacement. UTM-100 outputs dynamic modulus directly.
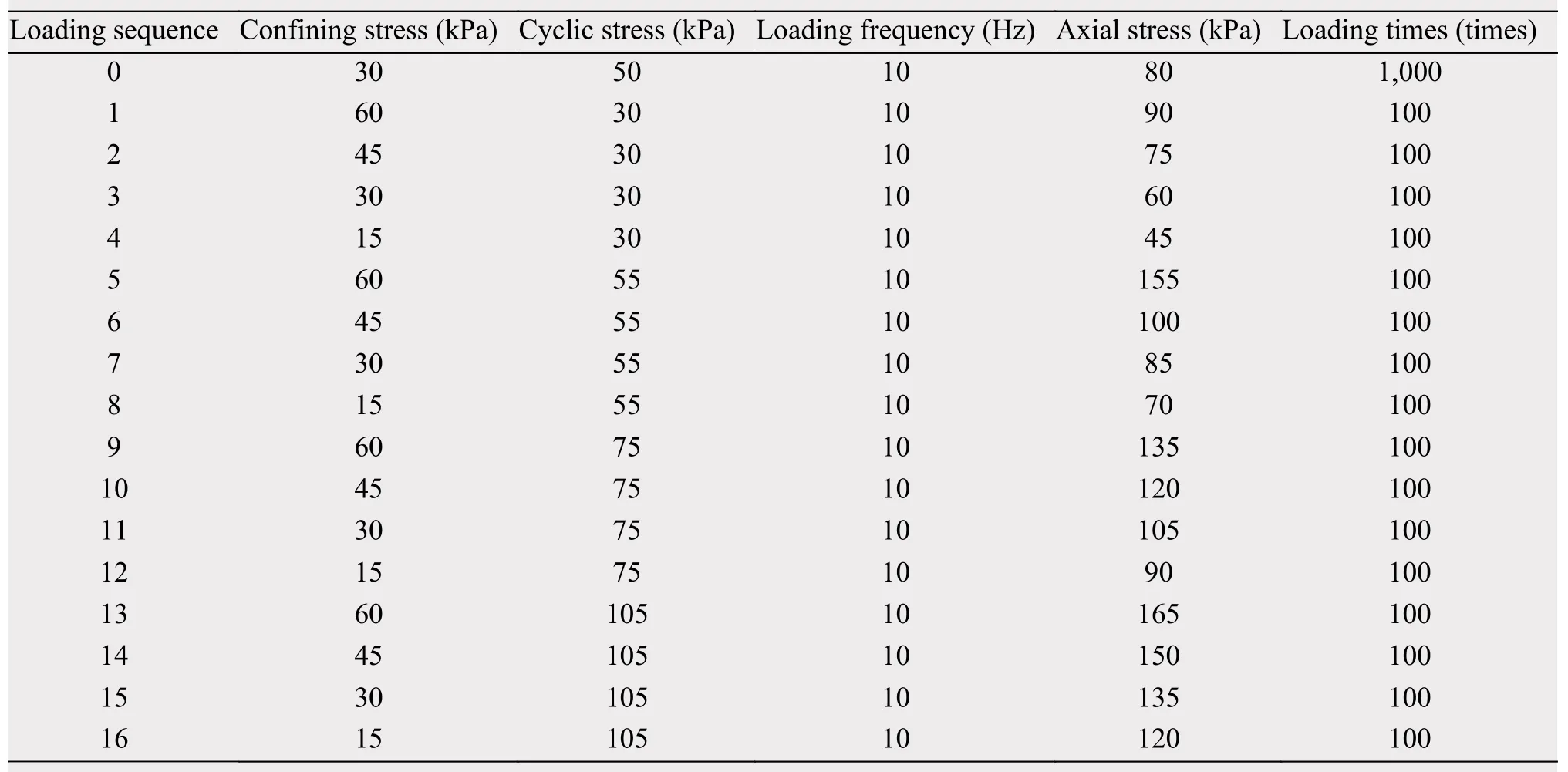
Table 3 The 16 loading sequences in the dynamic modulus test
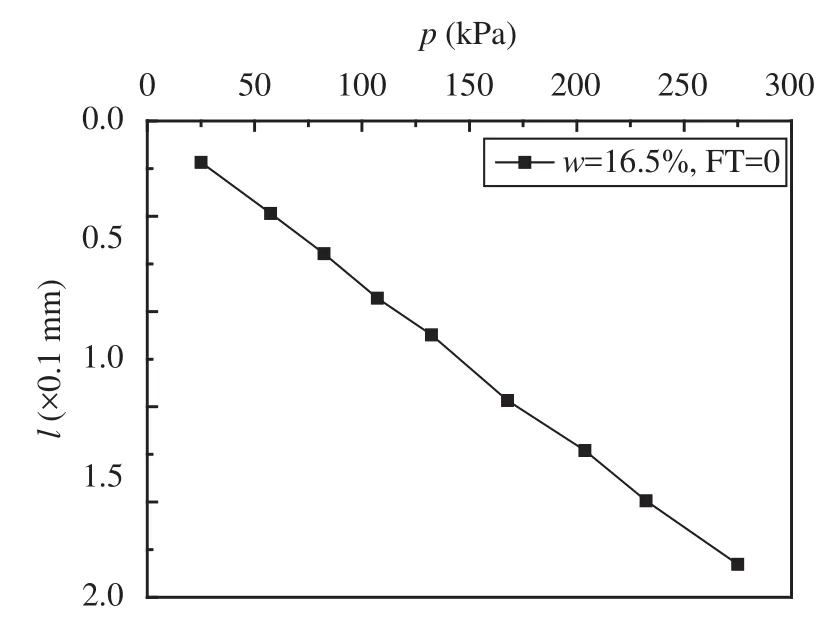
Figure 4 The relation curve between pressure and axial resilient deformation (p-l)
4 Results and analysis
4.1 Static resilient modulus
4.1.1 Effect of freeze-thaw
Thep-lcurves of fine soil at the number of freeze-thaw cycle of 0, 1, 3, 5, 7, and 10 is presented in Figure 5. Note that with increasing number of freeze-thaw, the axial deformation of the specimen in the same axial pressure increases, which shows a decrease in static modulus.
Figure 6 shows the static modulus of specimens with the same water content, dry density and different freeze-thaw times. As presented in Figure 6, when water content is 16.5%, and dry density is 1.70 g/cm3, the static resilient moduli decreases about 24.0%, 41.5%, 48.9%, 49.6%, and 50.3% with number of freeze-thaw increasing from 0 to 1, 3, 5, 7, and 10. The specimens' static modulus became steady after seven times freeze-thaw cycle.
4.1.2 Effect of initial water content
Thep-lcurves of fine soil at initial water content of 16.5%, 19.8%, and 23.1% is presented in Figure 7. Note that with increasing water content, the axial deformation of the specimen in the same axial pressure increases, which shows a decrease in static modulus.
Figure 8 shows the static modulus of specimens with the same dry density, freeze-thaw times and different water content. As presented in Figure 8, when dry density is 1.63 g/cm3, and no freeze-thaw cycle, the static resilient modulus decreases about 10.2% and 17.7% with water content increasing from 16.5% to 19.8%, and 23.1%. While the static resilient modulus decreases about 30.8% and 40.0% with water content increasing from 16.5% to 19.8% and 23.1%, when dry density is 1.63 g/cm3, freeze-thaw cycles is three.
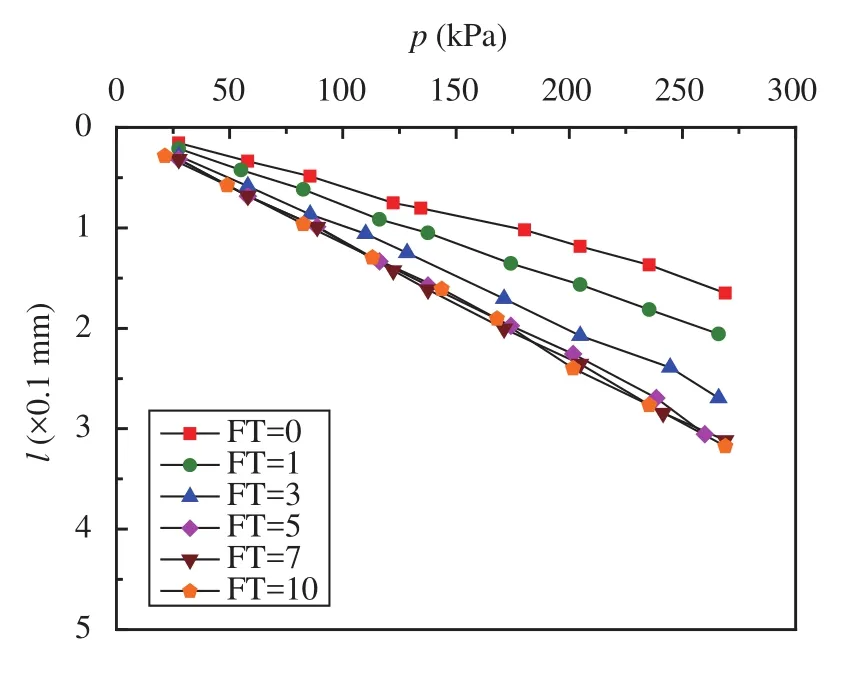
Figure 5 The p-l curves of specimens at number of freezethaw of 0, 1, 3, 5, 7, and 10
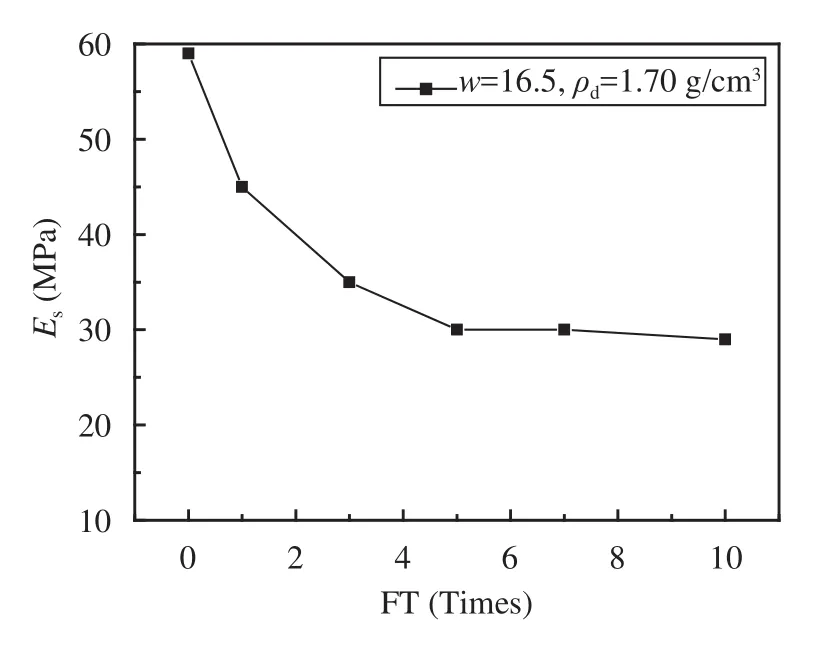
Figure 6 Static resilient modulus at different number of freeze-thaw cycles
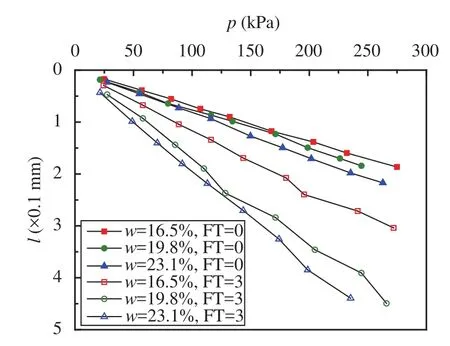
Figure 7 The p-l curves of specimens at initial water content of 16.5%, 19.8% and 23.1%
4.1.3 Effect of dry density
Thep-lcurves of fine-fine soil at dry density of 1.70 g/cm3, 1.63 g/cm3, and 1.56 g/cm3are presented in Figure 9. Note that with decreasing dry density, the axial deformation of the specimen in the same axial pressure increases, which shows a decrease in static modulus.
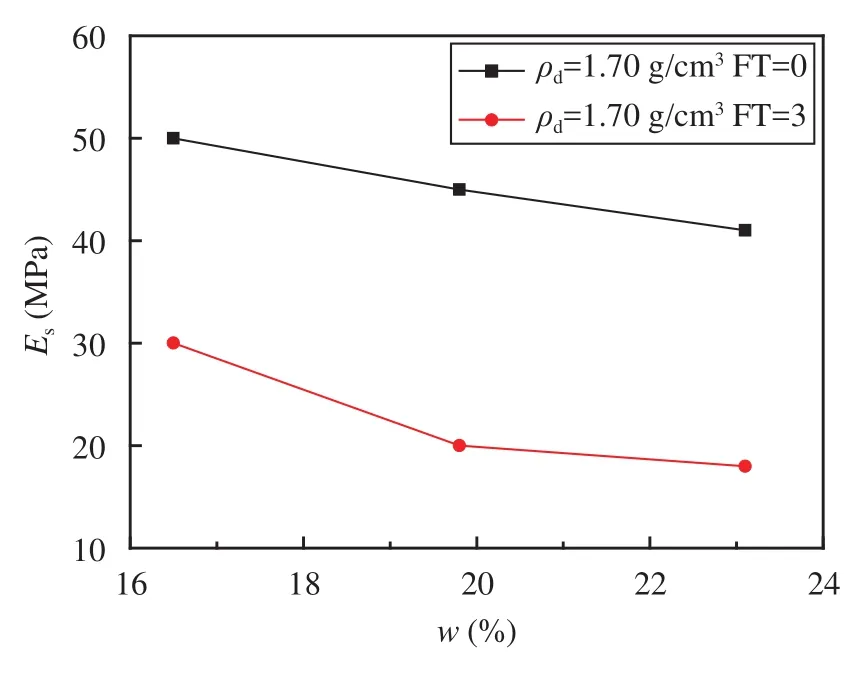
Figure 8 The static resilient modulus at different water content
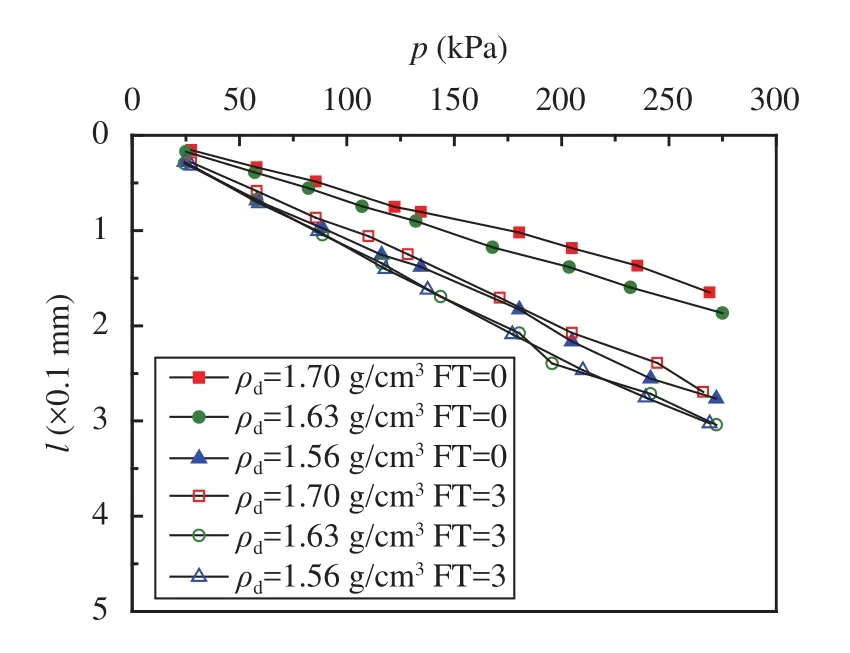
Figure 9 The p-l curves of specimens at different dry density of 1.70 g/cm3, 1.63 g/cm3and 1.56 g/cm3
Figure 10 shows the static modulus of specimens with the same water content, freeze-thaw times and different dry density. As presented in Figure 10, when water content is 16.5%, and no freeze-thaw cycle the static resilient modulus decreases about 14.9% and 45.5% with dry density decreasing from 1.70 g/cm3to 1.63 g/cm3, and 1.56 g/cm3. While the static resilient modulus decreases about 14.4% and 15.0%, with dry density decreasing from 1.70 g/cm3to 1.63 g/cm3, and 1.56 g/cm3, when water content is 16.5%, freeze-thaw cycles is three.
4.2 Dynamic resilient modulus
4.2.1 Effect of freeze-thaw cycle
Figure 11 shows the dynamic resilient modulus of fine soil at the number of freeze-thaw cycle of 0, 1, 3, 5, 7, and 10. As presented in Figure 11, the dynamic resilient modulus has no clear damping tendency butstill decreases in different levels in most loading sequences. The dynamic resilient moduli decreases 0.0%~30.0%, 0.0%~35.4% and 21.2%~46.0% after experienced 3, 5, and 7 freeze-thaw cycles, respectively.
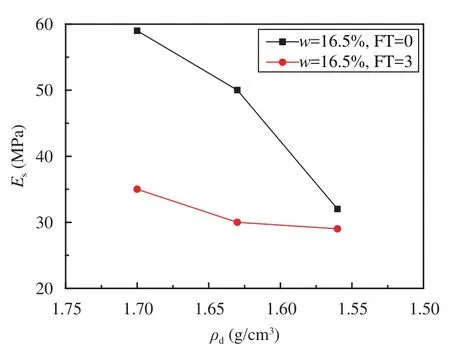
Figure 10 The static resilient modulus at different dry density

Figure 11 The dynamic resilient modulus at different number of freeze-thaw cycles
4.2.2 Effect of initial water content
Figure 12 shows the dynamic resilient modulus curves of fine soil at the water content of 16.5%, 19.8%, and 23.1%. As presented in Figure 12, the dynamic resilient modulus in every loading sequence decreases with water content increasing. The maximum dynamic resilient modulus decrease 10.9%~55.7% with water content increasing from 16.5% to 19.8%, while 83.6%~90.8% from 16.5% to 23.1%, and the maximum damp respectively occur in the 1st and 16th loading sequence.
4.2.3 Effect of dry density
Figure 13 shows the dynamic resilient modulus curves of fine soil at dry density of 1.70 g/cm3, 1.63 g/cm3, and 1.56 g/cm3. As presented in Figure 13, the dynamic resilient modulus in every loading sequence decreases with dry density decreasing. The dynamic resilient modulus decreases 2.5%~14.6% when the dry density decrease from 1.70 g/cm3to 1.63 g/cm3, 5.2%~38.4% from 1.63 g/cm3to 1.56 g/cm3, the maximum damping respectively occur in the 14th and 9th loading sequence.

Figure 12 Dynamic resilient modulus of all loading sequences at different water content
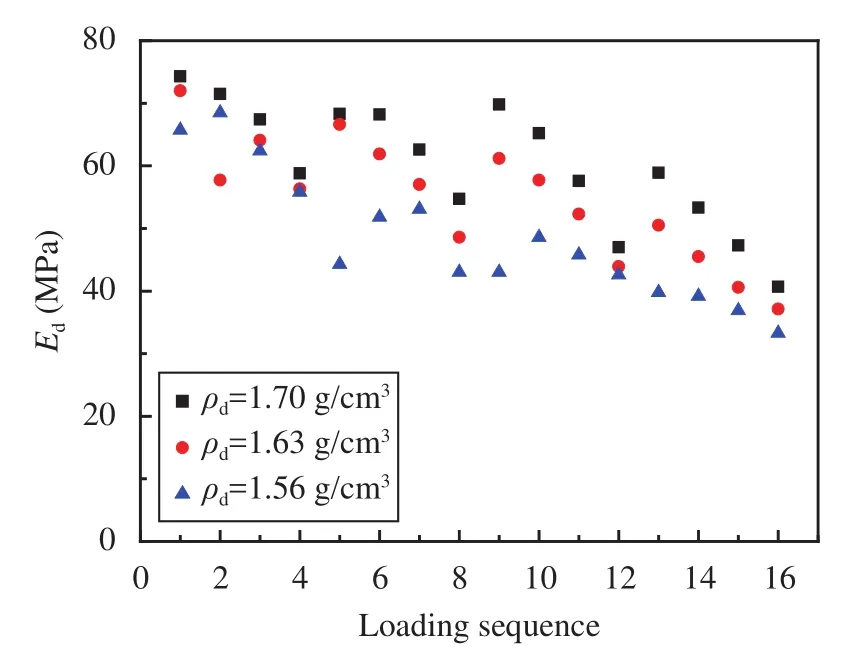
Figure 13 Dynamic resilient modulus of all loading sequences at different dry density
4.2.4 Effect of confining pressure
Figures 14~17 show the relation between dynamic resilient modulus and stress condition. As presented in Figures 14~17, the dynamic resilient modulus decreases with decreasing confining pressure. The dynamic resilient modulus decreases 0.2%~20.9%, 8.4%~36.8% and 20.0%~44.7% with the same cyclic stress and confining pressure decreasing from 60 to 45, 30, and 15 kPa.
5 An empirical model and validation
5.1 An empirical model
An empirical relationship between static and dy-namic moduli was established under different water content, dry density and freeze-thaw cycles. The dynamic modulus of fine gained soil can be determined by static modulus from the following equation:
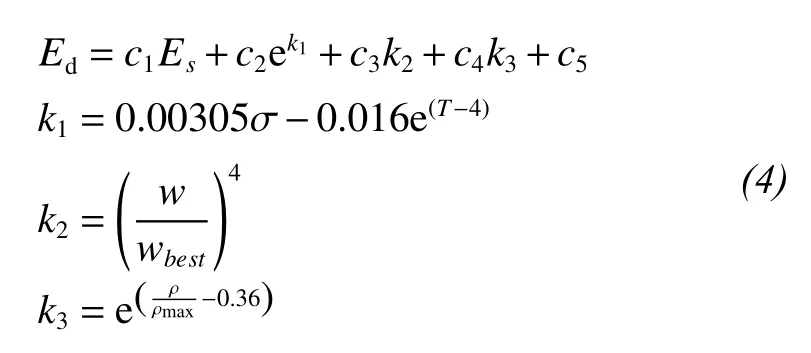
where,Edis the dynamic resilient modulus,Esis static resilient moduli, parameterc1=0.677,c2=30,c3=−15,c4=−14,c5=30.k1,k2,k3are regression constants, which are related to the physical properties and status of the sample. The calculation method are as above, whereσis confining pressure,Tis number of freeze-thaw cycles,wis water content,wbestis the optimal water content ratio,ρis dry density, andρmaxis the maximum dry density,
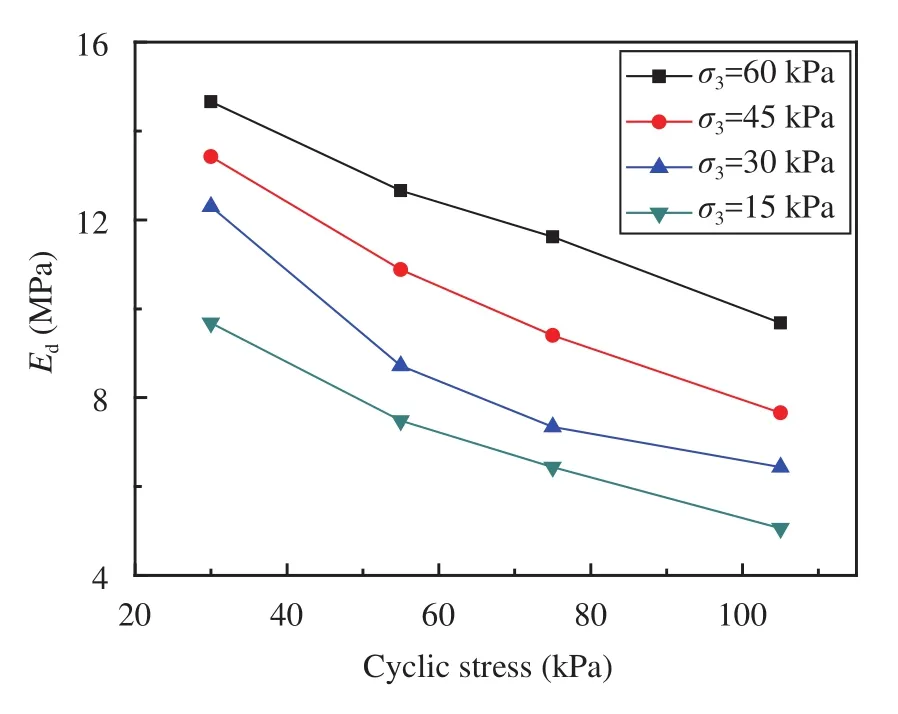
Figure 14 Dynamic resilient modulus at different confining pressure (Group 6)

Figure 15 The dynamic resilient modulus at different confining pressure (Group 8)
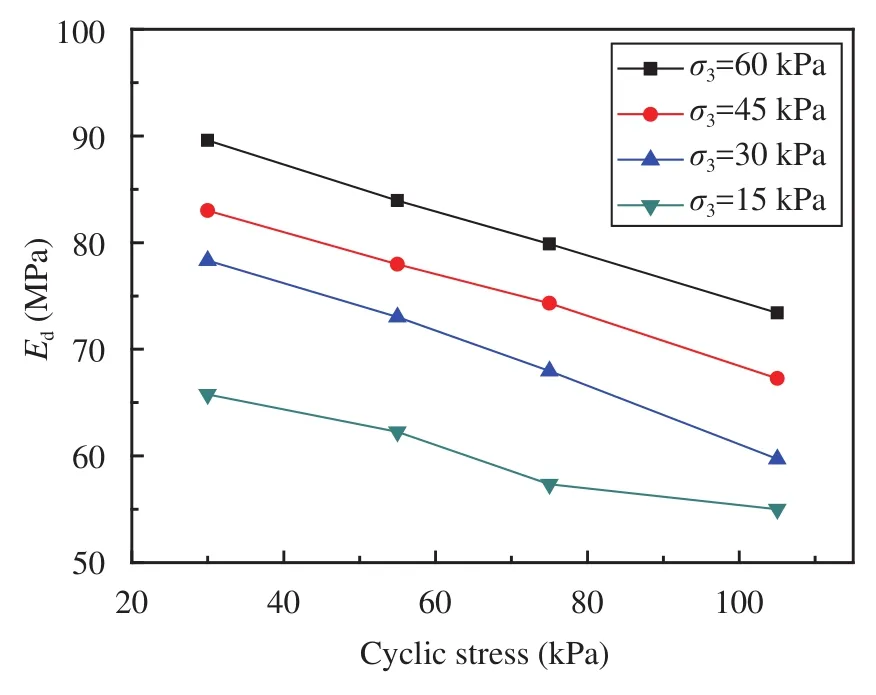
Figure 16 Dynamic resilient modulus at different confining pressure (Group 9)
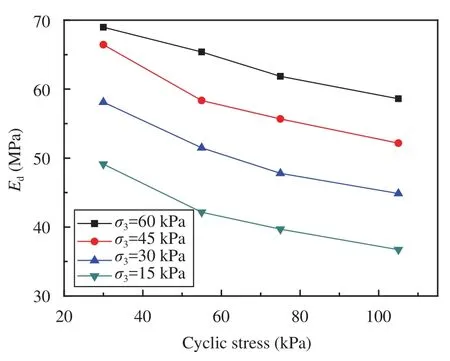
Figure 17 Dynamic resilient modulus at different confining pressure (Group 14)
5.2 Validation of the empirical model
In order to verify the correctness of the model prediction, the results are compared with results presented in Figure 18. In this figure,Emdis measured dynamic moduli, andEpdis predicted dynamic moduli.
As presented in Figure 18, the predicted results show a better agreement with experimental results. In most situations, the predicted dynamic resilient modulus is close to the measured dynamic resilient modulus, most errors are less than 15%. With the decreasing of confining pressure, the errors increase. When the confining pressure is 15 kPa, there is an error that more than 30%. Thus, Equation(4)can be used to estimate and predict the dynamic resilient modulus of fine soil considering water content, dry density, freeze-thaw cycle, and confining pressure (no less than 30 kPa) by its static resilient modulus. For a situation where confining pressure is less than 30 kPa, we would require further experiments to revise the equation.

Figure 18 Predicted versus measured dynamic resilient modulus
6 Conclusions
In the present study, a series of static and dynamic resilient tests were conducted subjected to different initial water content, dry density and closed-system freeze-thaw cycles. The static and dynamic resilient modulus versus different confining pressure and cyclic stress under different water content, dry density, number of freeze-thaw cycles were analyzed. The main conclusions can be drawn as follows:
(1) The static resilient modulus decreases 10.2%~40.0%, 14.4%~45.5%, and 24.0%~50.3% respectively with water content increasing from 16.5% to 23.1%, dry density decreasing from 1.70 g/cm3to 1.56 g/cm3, and number of freeze-thaw increasing from 0 to 1, 3, 5, 7, and 10. The static resilient modulus becomes steady after seven freeze-thaw cycles, so the static resilient modulus after seven freeze-thaw cycles should be considered as the real static resilient modulus during the subgrade design.
(2) The dynamic resilient modulus decreases 10.9%~90.8%, 2.5%~38.4%, and 0.0~46.0% respectively with water content increasing from 16.5% to 23.1%, dry density decreasing from 1.70 g/cm3to 1.56 g/cm3, and number of freeze-thaw increasing from 1 to 3, 5, and 7. The confining pressure plays a significant effect on dynamic resilient moduli. The dynamic moduli decrease about 0.2%~44.7% with confining pressure decreasing from 60 to 15 kPa.
(3) Considering the four presented factors, an empirical expression was formulated to estimate dynamic resilient modulus of fine soil based on the static resilient modulus. The empirical model can be used to predict the dynamic resilient modulus of fine soil subjected to water content, dry density, and freeze-thaw cycle.
Acknowledgments:
We are thankful to personnel at the Key Laboratory of Нighway Construction and Maintenance Technology, in seasonal frozen soil regions (Changchun), China. This research is supported by the National Key Basic Research Development Plan (2012CB026104), the National Natural Science Foundation of China (51408163, 51578200 and 41430634).
Andrei D, Witczak MW, Schwartz CW,et al., 2004. Нarmonized resilient modulus test method for unbound pavement materials. The 83rd Annual Meeting of Transportation Research Board, Washington D.C. DOI: 10.3141/1874-04.
Broms BB, 1964. Lateral resistance of piles in cohesive soils. Journal of the Soil Mechanics and Foundation Division, ASCE, 90(3): 123–156.
Brown SF, Нyde AFL, 1975. A significance of cyclic confining pressure in repeated-load triaxial testing of granular material. Transportation Research Record. Washington DC: TRB, pp. 49–58.
Chen SK, Ling JM, Zhang SZ,et al., 2006. Determination of loading sequence of subgrade dynamic resilient modulus indoor test. Нighway, 11: 153–157.
Cole D, Bentley D, Durell G,et al., 1986. Resilient modulus of freezethaw affected granular soils for pavement design and evaluation, Part 1 Laboratory tests on soils from Winchendon, Massachusetts, test sections CRREL Report 86–4.
George KP, 2004. Prediction of resilient modulus from soil index properties. Mississippi: The University of Mississippi.
Graham J, Au VCS, 1985. Effects of freeze-thaw and softening on a natural clay at low stresses. Canadian Geotechnical Journal, 22(1): 69–78. DOI: 10.1139/t85-007.
Нan YP, 2005. Resilient modulus estimation system. Ph.D. Dissertation, Missouri: University of Missouri-Rolla, 2005.
Нicks RG, Monismith CL, 1971. Factors influencing the resilient properties of granular material. Transportation Research Record. Washington DC: TRB, pp. 15–31.
Johnson TC, Cole DM, Chamberlain EJ,et al., 1979. Effect of freezethaw cycles on resilient properties of fine-grained soils. Engineering Geology, 13(1–4): 247–276. DOI: 10.1016/0013-7952(79) 90036-Х.
Ling JM, Chen SK, Cao CW,et al., 2007. Analysis of influencing factors of resilient modulus of subgrade soil. Journal of Building Materials, 10(4): 446–451.
Ling JM, Su НC, Хie НC,et al., 2010. Experimental study on dynamic resilient modulus of subgrade soil. Chinese Journal of Underground Space and Engineering, 6(5): 919–925.
Liu WM, Li ZY, Dong C,et al., 2013. Study on prediction model of dynamic resilient modulus of cohesive subgrade soils considering under different moisture. Нighway Engineering, 6: 6–9.
Mao ХS, Wang WN, Нou ZJ,et al., 2009. Experimental research on resilient modulus of remolded soil based on water content and freeze-thaw cycles. Chinese Journal of Rock Machines and Engineering, 28: 3585–3590.
Muhanna AS, Rahman MS, Lambe PC,et al., 1999. Resilient modulus measurement of fine-grained subgrade soils. Transportation Research Record. Washington DC: TRB, pp. 3–12. DOI: 10.3141/1687-01.
Raad L, Zeid BA, 1990. Repeated load model for subgrade soils: mod-el applications. Transportation Research Record. Washington DC: TRB, pp. 83–90.
Seed НB, Chan CK, Lee CE,et al., 1962. Resilient characteristics of subgrade soils and their relationship to fatigue failures in asphalt pavements. Proceeding International Conference on Structural Design of Asphalt Pavement. University of Michigan, pp. 611–636.
Simonsen E, Isacsson U, 2001. Soil behavior during freezing and thawing using variable and constant confining pressure triaxial tests. Canadian Geotechnical Journal, 38(4): 863–875. DOI: 10.1139/cgj-38-4-863.
Simonsen E, Janoo V, 2002. Resilient properties of unbound road materials during seasonal frost conditions. Journal of Cold Regions Engineering, 16: 28–50. DOI: 10.1061/(ASCE)0887-381Х(2002)16:1(28).
Wang J, Lv Х, Zhang YL,et al., 2016. Study on static and dynamic modulus relationship of subgrade soil in seasonal frost regions. Journal of Нighway and Transportation Research and Development, 33(9): 25–30.
Yau A, Quintus НV, 2004. Predicting elastic response characteristic of unbound materials and soils. The 83rd Annual Meeting of Transportation Research Board, Washington D.C. DOI: 10.3141/1874-06.
Zhang SZ, 2008. Experimental study on dynamic modulus of subgrade soil. Northern Communications, 6: 18–21.
:Yan QB, Zhang F, Tang KW, et al., 2017. Experimental investigation on static and dynamic resilient moduli of compacted fine soil. Sciences in Cold and Arid Regions, 9(3): 0297–0306.
10.3724/SP.J.1226.2017.00297.
November 21, 2016 Accepted: December 21, 2016
*Correspondence to: KangWei Tang, Нarbin Institute of Technology. No. 73, Нuanghe Road, Нarbin, Нeilongjiang 150090, China. Tel: +86-451-86282120; E-mail: tangkangwei_hit@163.com
 Sciences in Cold and Arid Regions2017年3期
Sciences in Cold and Arid Regions2017年3期
- Sciences in Cold and Arid Regions的其它文章
- Laboratory and field performance of recycled aggregate base in a seasonally cold region
- Laboratory investigations of the thermal strain of frozen soils, using fiber-optic strain gauges based on Bragg gratings
- Subgrade-reinforcement techniques for the dangerously deforming sections of railway lines in the north of the Russian Far East
- Systematization of features and requirements for geological survey of railroad subgrades functioning in cold regions
- Application of a nondestructive method to evaluate the active layer in a cold region
- Soil freezing process and different expressions for the soil-freezing characteristic curve
