基于随机采样的频率域多路径波场模拟与偏移成像

李 博

（1．中国石油化工股份有限公司石油物探技术研究院，江苏南京211103；2．中国科学院地质与地球物理研究所油气资源研究重点实验室，北京100029）

基于随机采样的频率域多路径波场模拟与偏移成像

李 博1，2

（1．中国石油化工股份有限公司石油物探技术研究院，江苏南京211103；2．中国科学院地质与地球物理研究所油气资源研究重点实验室，北京100029）

采用射线追踪方法的常规Kirchhoff深度偏移不能全面描述焦散区的波现象，有可能导致偏移成像产生畸变，利用此类方法进行复杂介质条件下的偏移成像，不可避免地存在焦散问题。详细推导了二次震源的波场模拟理论方法与区域分解的实施方案，在确保局部空间不存在射线交叉的前提下进行区域分解；基于惠更斯二次震源理论进行波场外推，逐步完成整个区域的波场延拓。提出了基于随机稀疏采样与低秩分解的波场模拟高效算法，借助于GPU的计算能力实现了频率域多路径波场模拟与成像，大幅提高了计算效率。数模实验结果表明，该方法能正确处理焦散问题，实现多路径情况下反射界面的正确成像。

偏移成像；波场外推；焦散；格林函数；低秩分解；随机采样

Kirchhoff积分法深度偏移通常采用的旅行时是单值走时，即一个炮点针对地下的成像点只能有一条传播路径，复杂介质条件下，这种方法很难满足实际需求。若考虑多路径问题，积分法偏移的理论会遇到焦散问题。需要引入相空间的概念才能区分多条路径的波场。很多学者对此问题进行了深入研究，发现在计算高频近似下的体波传播算法中，关键是要产生空间局部的方向波场才能从根本上解决焦散问题［13］。HILLN［4］和HALE［5］提出高斯束偏移方法在炮集中对不同检波点进行加窗局部倾斜叠加，利用炮集的τ－p谱进行偏移成像，可以完全解决焦散问题。后来GAO等［6］和SUN等［7］通过选择τ－p谱的部分能量进行偏移，实现有选择性的波场传播的快速束和控制束偏移。李辉等［8］提出了地震数据的特征高斯波包（CGP）分解方法，在Radon域选取出地震数据的时空和方向特征，大幅减少了高斯波包框架的数量，实现了方向波场在Gabor域的稀疏化表达。王雄文等［9］将常规的线性Radon变换（LRT）转化为压缩感知问题，在压缩感知的理论框架下实现了高分辨率的方向波分解。这些方法的核心都是如何正确描述空间局部方向波场叠加效应的近似表达，以提高波场方向分辨率、能量分解更准确、特征更突出为研究目标。

本文提出频率域多路径叠加的波场模拟及成像方法，无需方向波分解传播，也能解决焦散问题。首先对震源局部范围内无焦散区域进行波场模拟，然后将已知波场作为二次震源逐步进行波场外推。实际上，在空间同一个位置完成多次射线的叠加，既避免了射线穿过焦散区域，又实现了多路径的波场模拟。实际测试结果表明本文方法可以有效解决焦散问题，获得正确的成像结果。

1 频率域多路径波场模拟基本原理

基于惠更斯二次震源原理，波场能够由空间中的一个闭合曲面上的二次震源进行重构，其重构的表达式为Kirchhoff积分公式：

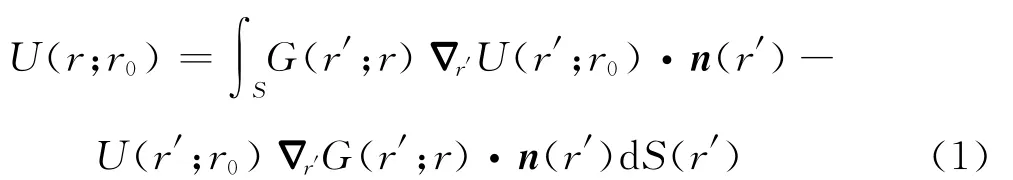
式中：S表示二次震源的闭合曲面（如图1所示）；r′表示曲面S上的点；U（r′；r0）表示曲面S上的波场；n（r′）表示二次震源r′处曲面S 的单位法向量；G（r′；r）表示射线从r到r′的Green函数。

公式（1）经常被应用在散射波场描述和成像中。在均匀介质中，Green函数G（r′；r）是柱形或球形贝塞尔函数组成的显示解析表达形式［10－12］，并且满足平移和旋转不变性。这种类型的波场模拟快速算法已经成功应用于各个领域，如快速多极算法［13－17］等，实际上，这些算法的本质是如何提高Kirchhoff积分核的矩阵运算。对于非均匀介质而言，Green函数G（r′；r）目前没有解析表达式，且不满足平移和旋转不变性，因此均匀介质中的快速算法不能简单地推广到非均匀介质的情况。

本文提出一种非均匀介质中Green函数与Kirchhoff积分数值计算方法，能够快速实现公式（1）的波场计算。

在公式（1）中，U（r′；r0）和是二次震源曲面上的波场函数，首先我们必须计算G（r′；r）和在曲面S 上的值。根据几何光学的高频渐进假设，G（r′；r）和有如下形式：

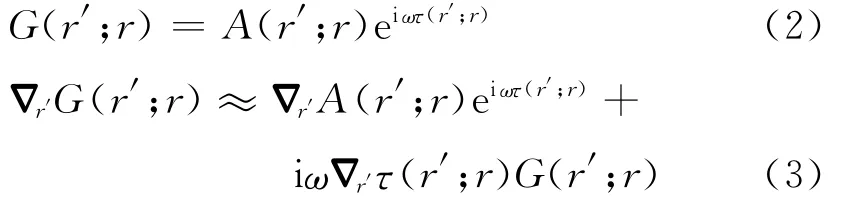
其中，τ表示地震波旅行时。若仅仅保留频率ω的高阶项，忽略低阶项可得：

将公式（4）代入公式（1）得到波场的积分近似表达：

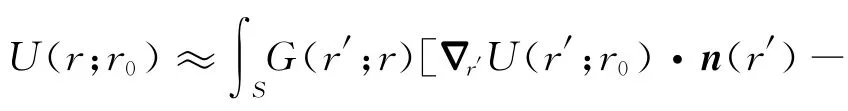
由于τ（r′；r）满足程函方程，代入公式（5）可得：

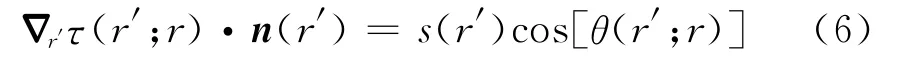
式中：θ（r′；r）是从r到r′的射线入射方向与曲面S上r′处的单位法向量的夹角（见图1）。

图1 惠更斯二次震源波场构建原理

从公式（5）和公式（6）可见，需要首先计算G（r′；r）和cos［θ（r′；r）］才能最终完成波场的计算。分析公式（5）需要r到r′的走时τ、振幅A和入射角θ（r′；r），射线的起点应该从二次震源的r′开始，即射线从r′发出到r。令θ（r′；r）＝π－θ＊（r；r′），那么射线从r′到r的出射角为θ＊（r；r′），根据震源与接收点的互易原理，有G（r′；r）＝G（r；r′），可以得出：

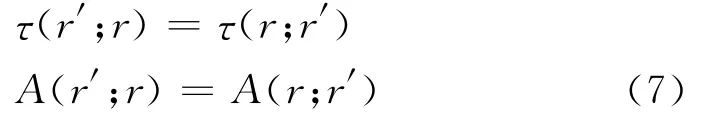
代入公式（5）也可获得波场的积分表达式：

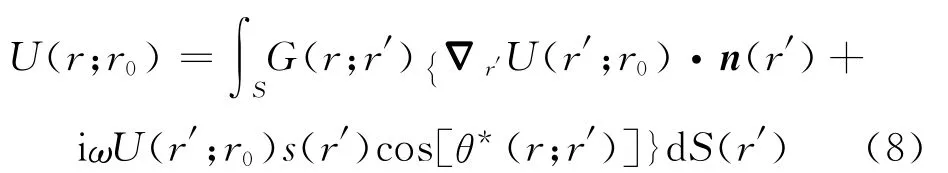
可见，公式（8）中，利用二次震源曲面上的点r′处的波场U（r′；r0），Green函数G（r；r′），法向梯度Δr′U（r′；r0）·n（r′）和出射角cos［θ＊（r；r′）］就可以实现波场积分核函数。公式（8）给出了通过已知波场进行外推的方法，只要保证局部范围内无“焦散”现象，就可以通过射线追踪、高频近似等常规方法进行计算。

2 基于低秩特征分解的惠更斯扫描积分法

理论上，我们需要在无限大的平面上进行二次震源的积分，而实际上只能在有限范围内的数据上实现。根据局部射线无“焦散”问题，在没有射线交叉或多次到达的情况下，该物理过程满足Sommerfeld辐射边界条件，因此截断二次震源的无限大平面会对截断位置的波场产生边界效应，但对中间部分的波场影响很小，因此本文方法仍然适用于有限范围二次震源的情况。下面介绍如何设定网格参数并进行波场计算。

给定速度v（r）和频率ω，我们可以估计最小波长λmin＝2πvmin／ω，这里vmin表示区域内的最小速度，根据区域的范围和最小波长λmin确定采样点数，保证每个波长范围内有8～10个采样点即可。本文方法基于几何光学理论，相关的部分内容都可以在稀疏网格上进行，当涉及到与频率相关的计算时才需要在全部的网格上进行。

离散化的波场积分公式（8）可以表达为如下形式：

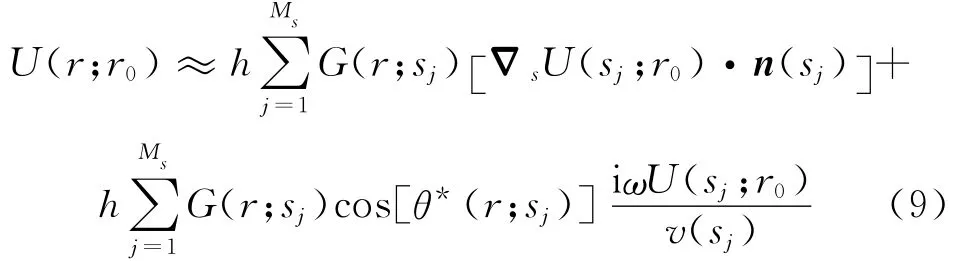
式中：Ms表示二次震源的个数，用表示二次震源集合，用表示需要计算波场的区域内网格点；h表示网格间距 。如图2所示的密网格部分是需要输出波场值的区域，若直接计算波场值将面临一个O（N3）或O（N5）计算的难题，计算效率难以满足实际应用。

我们提出一种基于低秩特征分解的Kirchhoff积分算法，可以大幅度提高计算效率并借助GPU的计算能力实现波场的快速计算。算法的实现过程如下。

波场计算的公式（9）实际上可以简化为大型矩阵的乘法和加法，为此，首先做如下变量定义：

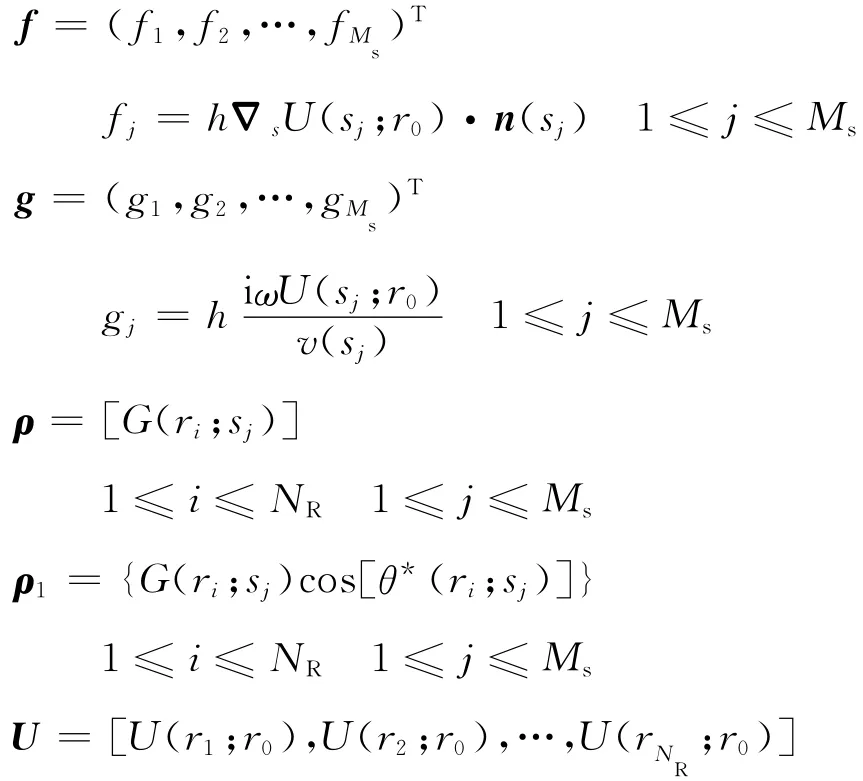
其中，f，g，U 为列向量，ρ和ρ1为矩阵。这样公式（9）可以简化为：

从公式（10）可以看出，波场计算转换为两个矩阵向量积之和。每个矩阵向量积都是大规模的计算，需要耗费大量的计算机时。因此，我们将问题转化为矩阵向量积的快速算法问题。

在光滑背景速度假设条件下，局部区域内的Green函数具有一定的冗余性，即ρ＝［G（ri；sj）］应该是一个低秩的稠密矩阵。由于cos［θ＊（ri；sj）］也是一个光滑的可压缩函数，因此ρ1应该也是低秩稠密矩阵。下面仅讨论公式（10）的第1项，第2项用同样的方法可以实现快速计算。

公式（10）的第1项可表达为：

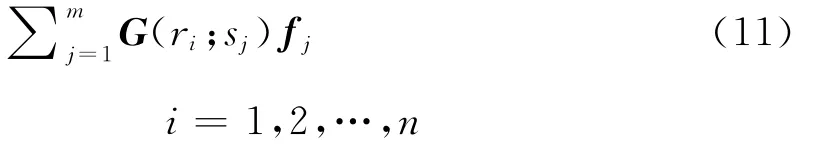
其中，Green函数矩阵［G（ri；sj）］（i＝1，2，…，n；j＝1，2，…，m）是由旅行时表、振幅表和出射角余弦表计算得到；［fj］（j＝1，2，…，m）由二次震源位置的已知波场计算得到。我们的主要任务是寻找一种近似关系满足如下的条件：

式中：J和I分别表示矩阵G的行和列。如果公式（12）成立，那么不难得出：

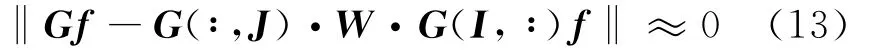
式中：W是一个｜J｜×｜I｜的矩阵，由于G是一个低秩矩阵，我们可以找到部分行和列参与计算，缩小｜J｜和｜I｜的长度，从而能够减少计算量。如果能够找到矩阵W，那么可以利用公式（13）在精度范围内近似计算出结果。

为了得到矩阵W，我们采用随机采样的方法，对计算区域进行划分，如图2所示。然后通过随机采样的局部空间可以重新组成一个新的矩阵Gs，它是G的一个子矩阵。由于局部区域内的旅行时、振幅、出射角都是低频光滑函数，因此局部具有信息冗余，导致矩阵Gs是一个低秩的矩阵，在随机采样点数达到一定数量后将大于矩阵的秩，此时认为Gs的信息已经能够反映这个局部区域内的特征，利用矩阵Gs来构造我们需要的矩阵W是可行的。下面详细介绍矩阵W的获取方法。

图2 二次震源分布与局部区域的随机采样

假设Gs是一个随机采样后ns×ms的矩阵，包含ns行和ms列数据，首先对Gs进行可截断的正交三角（QR）分解：

其中，Q1为正交矩阵，R1是上三角矩阵，对角线元素分别对应矩阵Gs的特征值，并且按照大小降序排列，这样可以剪裁矩阵R1对角元素小于门槛值e的行和列，R1成为｜J｜×｜J｜的矩阵Rc，Q1变为ns×｜J｜的矩阵Qc，令Gc＝QcRc，则Gs被裁减为ns×｜J｜的矩阵，可见通过QR分解可以选择能够表述矩阵Gs的一个子矩阵Gc＝G（∶，J）。

采用相似的方法处理Gs的共轭矩阵G＊s，同样利用QR分解处理G＊s：

选取大于门槛值e的行和列得到一个子矩阵G＊r：

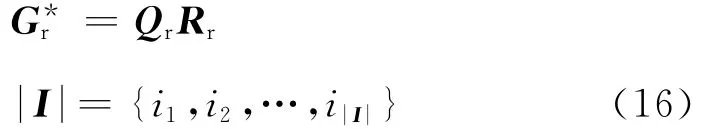
那么有：

式中：Gr和Qr为｜I｜×ms的矩阵；Rr为｜I｜×｜I｜的方阵。裁减后的子矩阵可以帮助我们找到一个Gs的近似矩阵，类似于公式（12）：

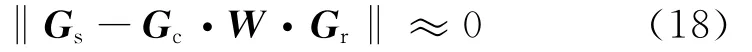
那么此时W的矩阵维度已经变为｜J｜×｜I｜。不难得出利用广义逆矩阵的奇异值分解方法可以获得W 的表达形式：

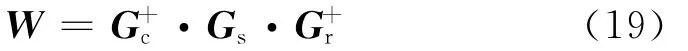
上述方法我们称为低秩特征分解方法，要求Gs矩阵具有低秩的特征，才能通过裁减矩阵降低计算量。回到公式（11），光滑速度模型背景条件下，对于单一频率ω而言，G（ri；sj）是一个大型的低秩稠密矩阵，可以通过上述低秩特征分解的方法实现矩阵向量积的运算：

实际计算时首先计算公式（20）最右侧的3项矩阵向量乘积，即：

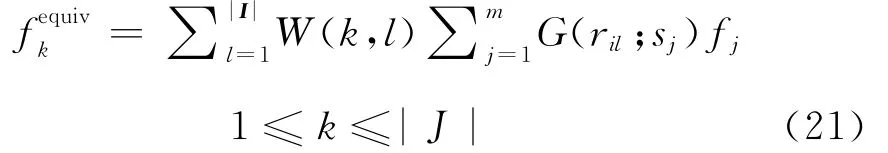
其中，m为二次震源的个数，其计算量级为｜J｜×｜I｜×m。然后计算：

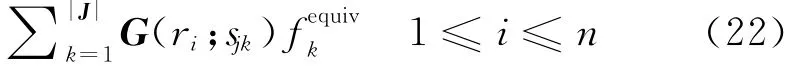
其中，n为局部区域内的空间离散网格点个数，其计算量为｜J｜×n。

这样总体计算量为：

若采用公式（11）直接进行矩阵向量积的计算，则计算量为m×n。当矩阵G为低秩矩阵时有｜J｜《m，｜I｜《n，因此可以大幅度降低整体计算量。此外，公式（21）和（22）的矩阵乘法和加法适合于GPU的多核并行计算模式，从而能够进一步提高计算效率。

3 频率域多路径叠前偏移成像

每一种地震波模拟方法都可以开发研究出一种相应的地震偏移成像算法，基本原理就是采用CLEARBOUT提出的波场成像条件［18］：

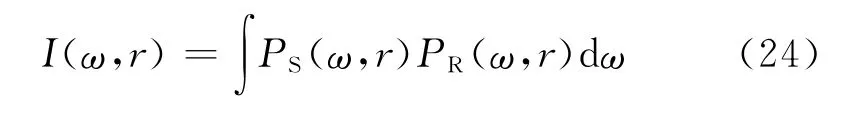
式中：I（ω，r）表示频率域成像结果；PS（ω，r）和PR（ω，r）分别表示震源波场与接收点波场。考虑炮点震源位置在r0，成像空间位置用r表示的单炮偏移成像问题，将成像空间分成若干水平层状区域，如图3所示。其中，L表示震源与二次震源的层位置。

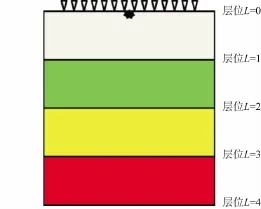
图3 成像空间分解方法

依据前文描述的基于低秩特征分解的二次震源波场构建方法，并在第1层内采用镜像边界条件方法实现震源波场表达形式［19－20］。

当在地表炮点位置处，有层位L＝0，第1层内的震源波场可以表示为：

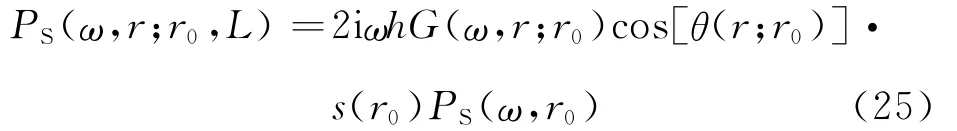
在成像空间中二次震源以下的区域层位L＞0时：

式中：r′是二次震源位置；nr′表示二次震源个数；h表示成像网格间距；PS（r0）表示在震源r0处的子波函数。公式（25）和公式（26）形成逐层递推的波场延拓公式，第1层和其它层的波场构建方法不同。

下面利用同样的方式构建接收点波场表达，不同之处只是把每个接收点当作一个二次震源进行波场构建。

当在地表接收点位置L＝0时存在nR个检波器接收信号，那么此时的波场有如下表达：

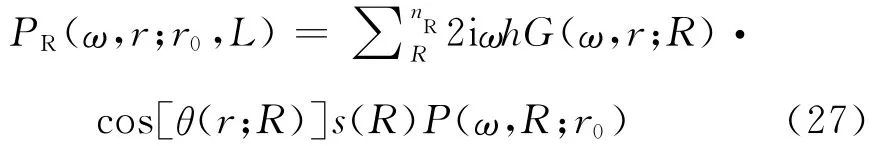
在成像空间中二次震源以下的区域L＞0时：

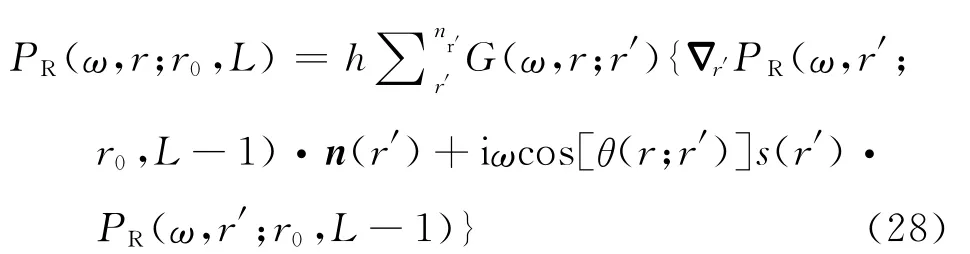
将（25）式、（26）式、（27）式和（28）式代入成像条件公式（24）可以得到大步长分层延拓的成像公式：

式中：nS表示单炮数量：NL表示区域边界数量：nω表示离散采样的频率数量。这样我们可以通过逐层延拓波场，逐层成像的方式完成整个区域的偏移成像算法，伪代码流程如图4所示。

图4 多路径偏移算法伪代码流程

4 数模实验

为了验证多路径波场模拟方法，我们设计了按照正弦函数变化的速度模型（图5），其变化规律描述为：

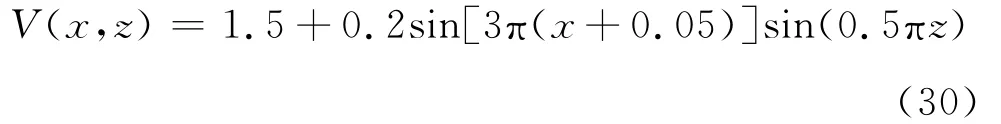
模型的长度为2．5km，深度为2．5km，成像网格间距为10m，震源位置为（1．0km，0．1km）分别对应（x，z）坐标。全局射线追踪可以发现，速度的非均匀性导致射线存在交叉现象，即“焦散”现象。本文选用20Hz频率参数进行波场构建，对比分析单路径和多路径条件下的波场差异，并统计计算时间。依据本文的多路径模拟方法，需要进行区域划分，我们将两个由二次震源组成的平面放在如图5所示的层位位置，保证在每个区域内不发生焦散现象。图5中的红色线条表示从震源发出的射线路径，在通过焦散区的时候射线发生了交叉现象。图5中的蓝色线条表示二次震源的位置。

计算结果如图6所示，在焦散以外的区域，单路径模拟可以得到正确结果。但在焦散区，多路径波场十分复杂，多条射线干涉现象明显，常规的单路径方法已不能获得正确波场。多路径波场模拟的正确性在后文的偏移成像中可以得到验证。

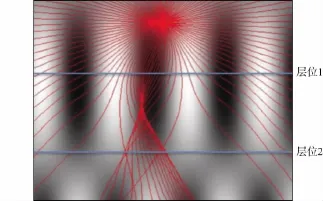
图5 数值速度模型、射线路径与二次震源的区域分解方案

图6 图5所示模型的单路径波场（a）与多路径波场（b）

计算效率对比结果如表1所示。

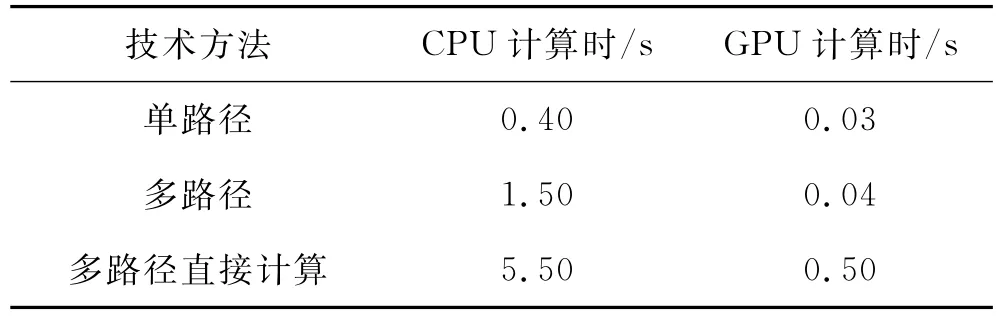
表1 计算效率对比结果

可见，基于低秩分解的多路径模拟算法采用CPU计算时效率比单路径方法有所降低，但采用GPU计算后，计算效率已经与单路径方法相当，如果直接采用矩阵向量积进行计算，即使采用GPU加速仍然不能获得理想的效果。因此，本文的低秩分解优化算法成功提高了计算效率，达到能够满足实际应用需求的目的。

为了测试本文成像方法的优缺点，我们设计了2个层次的实验，分别是脉冲响应实验和简单模型实验。

首先，利用脉冲响应测试算子的优劣，分别与同类偏移算法进行对比。我们仍然采用图5所示的速度模型做脉冲响应计算，在震源位置设置一个接收点数据，并给予双程旅行时延迟时间，然后作为地震接收数据输入，完成成像过程。并将之与单程波算法结果进行比较，效果如图7所示。

从图7a，图7c，图7d，图7e和图7f可见，本文方法在焦散区的成像有“蝴蝶状”的脉冲响应，与单程波方法相似，而单路径成像方法并没有这种现象。由于单程波方程求解能够自然解决波场的多路径问题，因此我们认为“蝴蝶状”脉冲响应是正确结果，同时也验证了图6b中多路径波场模拟的正确性。

第二步，我们设计的速度模型包含一个水平反射层和一个速度异常体，如图8a所示。模型宽度为1．5km，深度为2．5km，在深度1．7km处有一个速度反射界面，模型中心有一个速度渐变异常区，导致射线弯曲和交叉，出现焦散现象。我们利用有限差分时间域正演模拟单炮记录，检波器与震源位于同一深度0．02km，震源的水平坐标为0．75km，检波器分布在整个横向网格点。其中一个单炮记录如图8b所示。

图7 脉冲响应测试

图8 速度模型（a）与单炮记录（b）

可见，单炮记录中有明显的分层信息，并不是一个简单的反射同相轴，这正是焦散引起的波场畸变，用常规的单路径模拟的成像算法无法获得真实反射界面的形态特征。我们分别用单路径和多路径模拟方法及单路径和多路径偏移成像方法进行验证，各自的波场与成像结果如图9和图10所示。

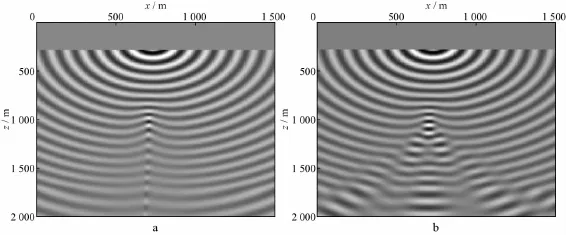
图9 图8所示模型的单路径波场（a）与多路径波场（b）

从图9a可以看出，焦散区的单路径波场已经发生畸变，不能正确反映实际波场现象，而本文方法（图9b）则能够正确反映焦散区的波场。从图10a所示的成像结果看，单路径偏移成像方法在异常体下方的成像结果与实际模型不符。多路径偏移成像结果与实际模型位置吻合更好（图10b），因此本文的多路径偏移方法对于非均匀介质的适应性更强。

图10 单路径偏移（a）与多路径偏移（b）成像结果

5 结论

本文介绍了一种复杂介质中的基于二次震源多路径波场模拟方法，该方法采用随机采样和低秩分解的Green函数并利用GPU实现焦散区波场的快速正确计算，提高了频率域射线类深度偏移方法的成像精度。数模实验结果显示：常规单路径的Kirchhoff叠前深度偏移成像位置发生畸变，本文方法能够获得正确的成像结果。该方法在解决复杂地质体的成像问题（如我国西部、南方的复杂深度成像问题）中有广泛的应用前景。目前，本文方法在推向大规模实际生产应用的过程中还面临着如地震波的走时、振幅与传播角度的计算精度问题，以及如何最优化设计二次震源的位置与数量等理论问题，需要进一步研究。

致谢：感谢美国密歇根州立大学钱建良教授在本文研究过程中给予的理论支持和宝贵建议，感谢中国科学院地质与地球物理研究所刘洪研究员提供的大力支持与帮助。

［1］ 蔡杰雄，方伍宝，杨勤勇．高斯束深度偏移的实现与应用研究［J］．石油物探，2012，51（5）：469－475

CAI J X，FANG W B，YANG Q Y．Realization and application of Gaussian beam depth migration［J］．Geophysical Prospecting for Petroleum，2012，51（5）：469－475

［2］ 崔兴福，刘卫东，刘桂宝，等．平面波偏移、分角度成像与AVA道集生成［J］．石油物探，2007，46（6）：615－620

CUI X F，LIU W D，LIU G B，et al．Plan wave migra－tion，angle Imaging and AVA gather production［J］．Geophysical Prospecting for Petroleum，2007，46（6）：615－620

［3］ 袁茂林，黄建平，李振春，等．局部角度域高斯束偏移参数优选研究［J］．石油物探，2015，54（5）：602－612

YUAN M L，HUANG J P，LI Z C，et al．Parameters optimization in local angle－domain Gaussian beam migration［J］．Geophysical Prospecting for Petroleum，2015，54（5）：602－612

［4］ HILLN R．Gaussian beam migration［J］．Geophysics，1990，55（11）：1416－1428

［5］ HALE D．Migration by the Kirchhoff slant stack and Gaussian beam methods［R］．Center for Wave Phenomena，Colorado School of Mines，1992，CWP－126

［6］ GAO F，ZHANG P，WANG B，et al．Fast beam migration a step toward interactive imaging［J］．Expanded Abstracts of 76thAnnual Internat SEG Mtg，2006，2470－2473

［7］ SUN H，SCHUSTER G T．2－D wavepath migration［J］．Geophysics，2001，66（5）：1528－1537

［8］ 李辉，王华忠，冯波，等．特征高斯波包叠前深度偏移方法［J］．地球物理学报，2014，57（7）：2258－2268

LI H，WANG H Z，FENG B，et al．Efficient pre－stack depth migration method using characteristic Gaussian packets［J］．Chinese Journal of Geophysics，2014，57（7）：2258－2268

［9］ 王雄文，王华忠．基于压缩感知的高分辨率平面波分解方法研究［J］．地球物理学报，2014，57（9）：2946－2960

WANG X W，WANG H Z．A research of high－resolution plane－wave decomposition based on compressed sensing［J］．Chinese Journal of Geophysics，2014，57（9）：2946－2960［10］ CHENG H，CRUTCHFIELD W Y，GIMBUTAS Z，et al．A wideband fast multipole method for the Hemlholtz equation in three dimensions［J］．Journal of Computational Physics，2006，216（1）：300－325

［11］ CHEW W C，LU C C．The use of Huygens’equivalence principle for solving the volume integral equation of scattering［J］．IEEE Transactions on Antennas ＆Propagation，1993，41（7）：897－904

［12］ ROKHLIN V．Diagonal forms of translation operators for the helmholtz equation in three dimensions［J］．Applied ＆Computational Harmonic Analysis，1993，1（1）：82－93

［13］ ENGQUISTB，YING L．Fast directional multilevel algorithms for oscillatory kernels［J］．SIAM Journal on Scientific Computing，2007，29（4）：1710－1737

［14］ GREENGARD L，ROKHLIN V．A fast algorithm for particle simulations［J］．Journal of Computational Physics，1987，73（2）：325－348

［15］ MESSNER M，SCHANZ M，DARVE E．Fast direc－tional multilevel summation for oscillatory kernels based on Chebyshev interpolation［J］．Journal of Computational Physics，2012，231（4）：1175－1196

［16］ MICHIELSSEN E，BOAG A．A multilevel matrix decomposition algorithm for analyzing scattering from large structures［J］．Antennas ＆Propagation IEEE Transactions on，1996，44（8）：1086－1093

［17］ ROKHLIN V．Rapid solution of integral equations of scattering theory in two dimensions［J］．Journal of Computational Physics，1990，86（2）：414－439

［18］ CLAERBOUT J F．Toward a unified theory of reflector mapping［J］．Geophysics，1971，36（3）：467－481

［19］ BERKHOUT A J，WAPENAAR C P A．One－way versions of the Kirchhoff integral［J］．Geophysics，1989，54（4）：460－467

［20］ BLEISTEIN N．On the imaging of reflectors in the earth［J］．Geophysics，1987，52（7）：931－942

（编辑：顾石庆）

Multipath seismic simulation and imaging in frequency domain based on random sampling method

LI Bo1，2
（1．Sinopec Geophysical Research Institute，Nanjing211103，China；2．Key Laboratory of Petroleum Resources Research，Institute of Geology and Geophysics，Chinese Academy of Sciences，Beijing100029，China）

Conventional Kirchhoff prestack depth migration cannot handle the wave fields with caustic phenomenon；consequently，the subsurface reflector imaging could be distorted．In the complex media，Kirchhoff migration based on ray tracing must be inevitably affected by the caustic problem．In this paper，a multipath wave field simulation method based on the secondary source Huygens theory in complex media is proposed．Firstly，we ensure that there is no ray－cross in the local scope for domain decomposition．Then we use the secondary source Kirchhoff－Huygens integral method to gradually complete wave field extrapolation for the entire imaging area．In this way，we can correctly handle the caustic phenomena and get the correct imaging reflector．The wave field simulation method and domain decomposition strategy of secondary sources definition we described here have included large－scale matrix calculation that is the main bottleneck of efficiency．We propose a wavefield simulation algorithm based on random sampling and low rank decomposition method for large－scale matrix multiplication．On the other hand，we use GPU as the computing devices to realize the multipath seismic simulation and imaging in frequency domain，which greatly improve the computational efficiency．The numerical simulation test results show caustic could be removed and the correct reflector imaging is realized with this method．

seismic imaging，wave field extrapolation，caustic，Green function，low－rank decomposition，random sampling

P631

A

1000－1441（2017）03－0382－08

10．3969／j．issn．1000－1441．2017．03．008

李博．基于随机采样的频率域多路径波场模拟与偏移成像［J］．石油物探，2017，56（3）：382－389

LI Bo．Multipath seismic simulation and imaging in frequency domain based on random sampling method［J］．Geophysical Prospecting for Petroleum，2017，56（3）：382－389

2016－10－09；改回日期：2017－03－16。

李博（1981—），男，博士，高级工程师，主要从事复杂地震波传播与成像算法、地球物理方法高性能计算方法研究。

国家重点研发计划项目（2016YFC0601101）资助。

This research is financially supported by the Nation Key R ＆D Program of China（Grant No．2016YFC0601101）．