奇异时滞系统时滞相关稳定性的新判据

王清超，吴保卫，郑宜强

(陕西师范大学 数学与信息科学学院，西安 710119)

【自然科学基础理论研究】

奇异时滞系统时滞相关稳定性的新判据

王清超，吴保卫，郑宜强

(陕西师范大学 数学与信息科学学院，西安 710119)

针对线性奇异时滞系统的时滞相关稳定性问题，提出了一种新的方法来讨论，与之前的方法相比较，这种方法研究出的结果具有较小的保守性。首先将奇异系统转化为带有线性约束的中立系统;其次应用Park’s Inequality方法，结合Lyapunov-Krasovskii泛函处理方法，得到了基于线性矩阵不等式的时滞相关稳定性的新判据;最后，通过实例表明，该方法得到的结论与其他文章相比减少了计算量且结论具有较小的保守性。

中立系统；时滞相关；Park’s Inequality；线性矩阵不等式

奇异系统又被称为描述系统、广义系统等，而奇异时滞系统广泛存在于工程系统中[1]，时滞的出现会对系统的稳定性造成不良影响[2-5]。文献[6-7]介绍了时滞相关稳定性与时滞无关稳定性，本文仅讨论奇异系统时滞相关稳定性，文献[8]讨论了小时滞对奇异系统稳定性的影响，但获得的条件具有较大保守性。文献[9]提出了一种新的方法讨论奇异时滞系统的时滞相关稳定性，得到了新的稳定性判据，但这些条件具有一定的保守性。

基于以上分析，为了减小稳定性判定的保守性，改变系统的稳定性能，本文主要用Park’s Inequality方法来讨论奇异时滞系统的时滞相关稳定性。在文中构建了Lyapunov-Krasovskii泛函并结合Park’s Inequality方法，获得了基于LMI的时滞相关稳定性的新判据。 最后，用实例表明用这一方法得到的结果具有较小的保守性。

1 预备知识

考虑如下奇异时滞系统：

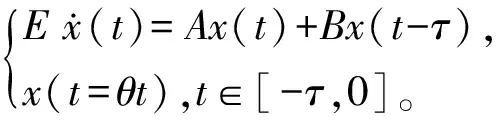
(1)

为了研究系统(1)的稳定性，引入以下定义和引理[1,10]：

定义1 如果det(sE-A)不恒为0，则称(E,A)是正则的。

定义2 如果deg(det(sE-A))=rank(E)，则称(E,A)无脉冲。

引理1 若(E,A)正则、无脉冲，则系统(1)在[0,+)上存在唯一解且无脉冲。

引理2 假设(E,A)正则、无脉冲，则存在可逆矩阵M,N,使得下式成立：

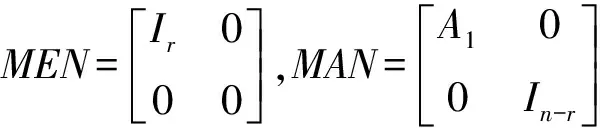
(2)

如果(E,A)是正则、无脉冲的，根据引理2，存在可逆矩阵M,N∈Rn×n，使得

(3)

那么可以将系统(1)转化成中立系统。

令

(4)

系统(1)等价于下边的等式

(5)

对矩阵进行适当分块，等式可以写成以下的式子：

(6)

0=v2(t)+Bs3v1(t-τ)+Bs4v2(t-τ)。

(7)

对(7)式求导得

(8)

联合(7)(8)式得到

(9)

联立(6)式和(9)式推出

(10)

令

(11)

由此可将系统(1)转化为中立系统的形式

(12)

因为x(t)=θ(t)，所以v(t)=N-1x(t)，显然可知，如果中立系统(12)渐进稳定，那么奇异系统(1)也渐进稳定。

2 主要结果

下面主要通过讨论中立系统(12)的稳定性来说明奇异系统(1)的稳定性，为了讨论方便，在给出主要结果之前给定以下假设和引理：

假设1 假设矩阵对(E,A)是正则和无脉冲的。

引理3[11]令a(α)∈Rnx，b(α)∈Rny，α∈Ω，那么对于任意给定的正定矩阵X∈Rnx×nx，任意的矩阵M∈Rnx×ny，都有以下不等式成立：

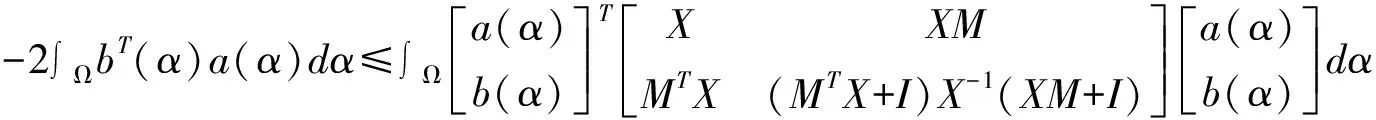
(13)

引理3的内容是证明定理1的主要引理，下面根据Lyapunov-Krasovskii稳定性定理，建立中立系统(12)渐进稳定的充分条件。

(14)

证明 首先构造如下形式的Lyapunov-Krasovskii函数：

V(t)=V1+V2+V3+V4。

其中：

V1=vT(t)Pv(t)，

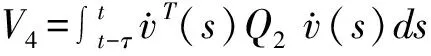
V1对t求导可以得到如下的等式

(15)

分别对V2,V3,V4求导得：

经整理可得

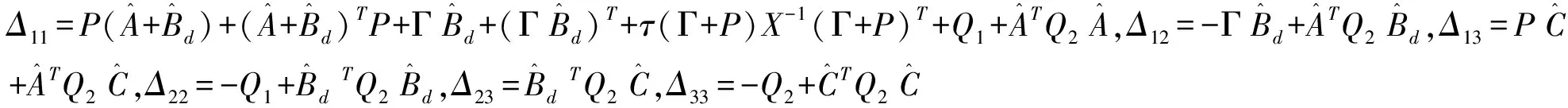
3 数值算例

在这一部分，我们通过算例来验证本文给的稳定性判据具有较小的保守性。

例1 考虑如下的线性中立系统

解析 根据定理1以及利用线性矩阵不等式求解方法，这里的求解程序为：

setlmis([]);P=lmivar(1,[2 1]);Q1=lmivar(1,[2 1]);Q2=lmivar(1,[2 1]);V=lmivar(1,[2 1]);W=lmivar(1,[2 1]);t=lmivar(1,[1 1]);lmiterm([1 1 1 P],1,A+B,′s′);lmiterm([1 1 1 Q1],1,1);lmiterm([1 1 2 P],1,C);lmiterm([1 1 4 Q2],A′,1);lmiterm([1 2 2 Q2],1,1);lmiterm([1 2 4 Q2],C′,1);lmiterm([1 3 3 V],1,1);lmiterm([1 4 4 Q2],1,1);lmiterm([-2 1 1 Q2],1,1);lmiterm([-3 1 1 Q1],1,1);lmiterm([-4 1 1 P],1,1);lmiterm([-5 1 1 V],1,1);G=getlmis;[tmin b]=feasp(G);

利用MATLAB求解，得时滞最大上界为：1.6010。

通过这几篇文章在相同情况下的比较，很明显地能够看出来本文得到的稳定性条件具有较小的保守性。

4 结语

本文通过研究中立系统的稳定性来研究奇异时滞系统的稳定性。文中提出了一种新的方法，用积分不等式法研究奇异时滞系统的时滞相关稳定性。在符合一定条件下将奇异系统转化为带有约束的中立系统，通过合理的不等式放缩方法，并结合Park’s Inequality来研究。与以前同类研究结果相比较，本文没有直接研究奇异时滞系统，而是通过将奇异系统转化为中立系统来研究，结合新的李雅普诺夫泛函的选取给出了基于线性矩阵不等式(LMI)的时滞相关稳定性新判据，用这一方法得到的系统稳定的时滞上界比已有的文献具有较小的保守性，并通过数值算例说明了本文方法的有效性。

[1] Niculescu S I.Delay Effects on Stability:A Robust Control Approach[M].Berlin：Springer,2001.

[2] Li H Y，Jing X J,Karimi H R.Output-feedback-based control for vehicle suspension systems with control delay[J].IEEE Trans.Ind.Electron，2014，61(1)：436-446.

[3] Chen B Y,Zheng W X.Stability analysis of time-delay neural networks subject to stochastic perturbations[J].IEEE Trans.Cybern，2013，43(6)：2122-2134.

[4] Lu J Q，Ho D W C，Cao J D.Synchronization in an array of nonlinearly coupled chaotic neural networks with delay coupling[J].Int.J.Bifurc.Chaos，2008，18(10)：3101-3111.

[5] Lu D R，Li H，Zhu Y.Quantized H-infinity filtering for singular time-varying delay systems with unreliable communication channel[J].Circuits Syst.Signal Process，2012，31(2)：521-538.

[6] Wu Z G，Su H Y，Chu J.Improved results on delay-dependent control for singular time delay systems[J].Acta Autom.Sin，2009，35(8)：1101-1106.

[7] Sun X，Zhang Q L，Yang C Y.An improved approach to delay-dependent robust stabilization for uncertain singular time-delay systems[J].International Journal of Automation and Computing，2010，7(2)：205-212.

[8] Fridman E.Effects of small delays on stability of singularly perturbed systems[J].Automatic，2002，38:897-902.

[9] Fridman E.Stability of linear descriptor systems with delay:a Lyapunov-based approach[J].Math Anal Appl，2002，273:24-44.

[10]XuSY，DoorenPV，StefanR.Robuststabilityandstabilizationforsingularsystemswithstatedelayandparameteruncertainty[J].IEEETrans.Autom.Control，2002，47(7)：1122-1128.

[11]HaleJK，SjoerdM，LunelV.IntroductiontoFunctionalDifferentialEquations[M].NewYork：Springer，1993.

[12]MahmoundMS.Robuststabilityandstabilizationofaclassofuncertainnonlinearsystemswithdelays[J].JournalofMathematicalProblemsinEngineering，1998，(4):165-185.

[13]BoydSL,GhaouiEI，FeronE.Linearmatrixinequalityinsystemsandcontroltheory[M].Philadelphia:SIAM,1994.

[14]FridmanE.NewLyapunov-Krasovskiifunctionsforstabilityoflinearretardedand-neutraltypesystems[J].Syst.ControlLett，2001，43：309-319.

[15]ChenJD，LienCH，FanKK.CriteriaforasymptoticstabilityofaclassofneutralsystemsviaaLMIapproach[J].IEEEProc.ControlTheoryAppl，2001，148：442-447.

[16]LienCH，ChenJD.Discrete-delay-independentanddiscrete-delay-dependentcriteriaforaclassofneutralsystems[J].ASMEJ.Dyn.Syst.Meats.Control,2003,125:33-41.

【责任编辑 牛怀岗】

NewMethodonDelay-dependentStabilityforSingularSystemwithDelay

WANGQing-chao，WUBao-wei，ZHENGYi-qiang

(CollegeofMathematicsandInformationScience，ShaanxiNormalUniversity，Xi’an710119，China)

A new method is proposed to study the delay-dependent stability conditions of the linear singular time-delay system，the result of the new method is less conservativeness than the before.Firstly，by representing the singular system as a neutral system with a linear constraint.Secondly，using the Park’s inequality and combing the lyapunov-krasovskii functional method，we obtain a new delay-dependent stability criterion in terms of a linear matrix inequality.Finally，illustrative examples show the new result reduces the amount of computation and is less conservativeness than before.

neutral system; delay-dependent; Park’s inequality; linear matrix inequality

TP273

A

1009-5128(2017)08-0021-05

2016-11-23

国家自然科学基金项目：具有输入时滞的切换非线性系统的稳定性分析与控制器设计(61403241)

王清超(1989—)，男,河南开封人，陕西师范大学数学与信息科学学院硕士研究生;吴保卫(1963—)，男,陕西西安人，陕西师范大学数学与信息科学学院教授，博士研究生导师，主要从事控制理论研究。