应变能最小的保形有理四次样条插值曲线
张 澜,赵前进
(安徽理工大学 数学与大数据学院,安徽 淮南 232001)
【自然科学基础理论研究】
应变能最小的保形有理四次样条插值曲线
张 澜,赵前进
(安徽理工大学 数学与大数据学院,安徽 淮南 232001)
为构造光顺的保形有理四次样条插值曲线,以形状控制参数和插值函数在节点处的导数为决策变量,以插值曲线应变能最小为目标函数,以插值函数保形以及形状控制参数和节点处的导数大于0作为约束条件,建立优化模型,求解获得应变能最小的保形有理四次样条插值曲线。给出的数值实例表明新方法能获得光顺的插值曲线。
有理四次样条插值;保形;应变能;最优化
利用有理样条进行保形插值是几何造型领域中的研究热点之一[1-8]。文献[4-6]介绍的保形有理四次样条插值函数节点处导数的算法为构造光顺的保形有理四次样条插值曲线,以形状控制参数和节点处的导数为决策变量,以插值曲线应变能最小为目标函数,以插值函数保形以及形状控制参数和节点处的导数大于0作为约束条件,建立优化模型,给出插值算法是求解获得应变能最小的保形有理四次样条插值曲线。
1 插值函数[4]
给定数据{(xi,fi),i=1,2,…,n},其中:fi为被插值函数在节点xi处的函数值,此处令x1 (1) 其中: Pi(t)=αifi(1-t)4+Ui(1-t)3t+Vi(1-t)2t2+Wi(1-t)t3+βifi+1t4, (2) Qi(t)=αi(1-t)+βit, Ui=(3αi+βi)fi+αidihi, Vi=3βifi+1+3βifi。 (3) 插值函数s(x)在节点xi处的一阶导数值为di,αi,βi被称为形状控制参数且αi>0,βi>0 。 由(2)(3)式易知,有理样条插值s(x)满足下列插值性质: s(xi)=fi,i=0,1,…,n。 (4) 如果f(x)在区间[a,b]上有x1 di≥0,i=1,2,…,n。 (5) 在区间[xi,xi+1]上,s(x)单调递增的充要条件为: s′(x)≥0,i=0,1,…,n-1。 (6) 对(1)式中定义的插值函数s(x)求导: (7) 其中: Qi0=αi2di,Qi1=2αi2(3Δi-di),Qi2=3αiβi(4Δi-di-di+1),Qi3=2βi2(3Δi-di+1),Qi4=βi2di+1。 因为(7)式给出的插值函数s(x)的导数s′(x)的分母恒为正,所以只需s′(x)的分子大于0即可。当di≥0时,有Qi1≥0,Qi4≥0 ,因此插值函数s(x)单调的充要条件为:Qij≥0,j=1,2,3。即 Qi1=2αi2(3Δi-di)≥0, Qi2=3αiβi(4Δi-di-di+1)≥0, (8) Qi3=2βi2(3Δi-di+1)>0。 由(8) 式得到函数s(x)单调的充要条件为: di≤3Δi,di+1≤3Δi,di+di+1≤4Δi。 (9) 由文献[8]得出下列结论: 已知单调递增数据f1≤f2≤…≤fn,导数值di≥0,只要di满足(9)式时,就存在含有正参数αi,βi的有理四次样条插值函数s(x)∈C1[a,b],并且是单调递增的。 对(1)式求二阶导数并化简可得: (10) 其中: Bi0=2αi3(3Δi-2di)-2αi2βidi, Bi1=6αi2βi(3Δi-di+1)+2αi3(di-3Δi)-8αi2βidi, Bi2=6αi2βi(di-3Δi)+6αiβi2(3Δi-di+1), (11) Bi3=6αiβi2(di-3Δi)+2βi3(3Δi-di+1)+8αiβi2di+1, Bi4=2βi3(2di+1-3Δi)+2αiβi2di+1。 因此有 (12) (13) 由函数s(x)在xi处二阶连续,可得 (14) 由此得出如下结论: 当插值导数di满足(14)式时,含有形状控制参数αi,βi的有理四次样条插值函数s(x)在区间[a,b]上二阶连续。[9] 插值曲线的研究主要应用在物体外形设计上,因此插值曲线不仅要求过插值节点,还要求曲线能够保光顺性、保凹凸性等。研究曲线光顺性会发现光顺准则是最基本的问题,人们在不同的实际问题中,对曲线光顺的要求不同,使得对曲线光顺的认识也不同。一般认为应变能最小的曲线是光顺的,在曲线光顺的研究中常常以曲线能量较小作为约束条件。[10-12] 插值函数s(x)在[x0,xn]区间上C2-连续曲线的应变能定义如下: (15) 积分化简得 (16) 其中: 为构造光顺的保形有理四次样条插值曲线,以形状控制参数αi,βi和节点处的导数di为决策变量,以插值曲线应变能最小为目标函数,以插值函数保形以及形状控制参数αi,βi和节点处的导数di大于0作为约束条件,建立优化模型 (17) s.t. αi,βi>0,i=0,1,…,n-1, (18) di>0,i=0,1,…,n, (19) di≤3Δi,di+1≤3Δi,di+di+1<4Δi,i=0,1,…,n-1。 (20) 求解此优化模型得最优参数αi,βi和di,进一步得到光顺的保形有理四次样条插值曲线。 表1 形状参数αi,βi和导数di的值 由文献[13-14]知,保形有理四次样条插值函数的误差有以下结论: 定理1 设f(x)∈C2[a,b],s(x)是f(x)如(1)式所定义的有理样条插值函数,对给定的αi,βi,则x∈[xi,xi+1],i=0,1,…,n-1,有 给出一组单调递增的数据x1=0,x2=6,x3=10,x4=29.5,x5=30,f(x1)=0.01,f(x2)=15,f(x3)=15,f(x4)=25,f(x5)=30。 由本文方法建立模型求解最优形状参数αi,βi和插值节点处导数di的值如表1所示。 依表1数据绘制出应变能最小且保形的有理四次样条插值曲线(如图1),并与文献[6]中插值法所绘制的插值曲线(如图2)作对比,验证了新方法的有效性。 图1 由新方法得到的有理样条插值曲线 图2 由文献[6]得到的有理样条插值曲线 [1]DelbourgoR,GregoryJA.Shapepreservingpiecewiserationalinterpolation[J].SiamJournalonScientific&StatisticalComputing,1984,6(4):967-976. [2]MinJ,ChenBK.Akindofrationalquarticinterpolationsplineanditsapproximationproperties[J].NumericalMathematicsAJournalofChineseUniversities,2007,29(1):57-62. [3]HanX.Convexity-PreservingPiecewiseRationalQuarticInterpolation[J].SiamJournalonNumericalAnalysis,2008,46(2):920-929. [4] 王强.有理插值样条方法及其在数字图像处理中的应用研究[D].合肥:合肥工业大学博士学位论文,2007:41-44. [5] 邓四清,蔡时荣,孙宇峰.一种带导数的有理四次插值样条曲线的区域控制[J].韶关学院学报,2012,33(12):5-9. [6]CukupS,BaikL,KuartikI,etal.ImprovedSufficientConditionsforMonotonicPiecewiseRationalQuarticInterpolation[J].SainsMalaysiana,2011,40(10):1173-1178. [7] 邓四清.一类加权有理四次插值样条曲线的形状控制[J].计算机工程与应用,2014,50(2):137-141. [8] 刘琳,唐月红.一类四次有理样条的形状控制及其逼近性质[J].数值计算与计算机应用,2010,31(4):241-252. [9]WangQ,TanJQ.Rationalquartiesplineinvolvingshapeparameters[J].JournalofInfmation&ComputationalScience,2004,(1):127-130. [10] Duan Q,Bao F,Du S,et al.Local control of interpolating rational cubic spline curves[J].Computer-Aided Design,2009,41(11):825-829. [11] Bao F,Sun Q,Pan J,et al.A blending interpolator with value control and minimal strain energy[J].Computers & Graphics,2010,34(2):119-124. [12] Zhang C,Zhang P,Cheng F.Fairing spline curves and surfaces by minimizing energy[J].Computer-Aided Design,2001,33(13):913-923. [13] 闵杰,陈邦考.一种四次有理插值样条及其逼近性质[J].高等学校计算数学学报,2007,29(1):57-62. [14] 段奇,刘爱奎,张玲,等.几种有理插值函数的逼近性质[J].高等学校计算数学学报,2000,22(1):55-62. 【责任编辑 牛怀岗】 ShapePreservingRationalQuarticSplineInterpolationCurveofMinimumStrainEnergy ZHANGLan,ZHAOQian-jin (SchoolofMathematicsandBigData,AnhuiUniversityofScienceandTechnology,Huainan232001,China) In order to obtain the most fairing shape preserving rational quartic spline interpolation curve,an optimization model is established,with the shape control parameters and the derivative of the interpolation function at the nodes being decision variables,the minimum strain energy of the interpolation curve being the objective function,and the interpolation function for monotony as well as the shape control parameters and the derivative of the node greater than zero being the constraint conditions.The shape preserving rational quartic spline interpolation curve with minimum strain energy is obtained based on the optimization model.The numerical examples are given to show that the new method can obtain fairing interpolation curve. rational quartic spline interpolation; shape preserving; strain energy; optimization O241.3 A 1009-5128(2017)08-0016-05 2016-12-30 国家自然科学基金项目:有理插值新方法及其在三维数字模型信息保护中的应用研究(60973050);安徽省教育厅自然科学基金项目:有理插值新方法及其应用研究(KJ2009A50) 张澜(1990—),女,河南南阳人,安徽理工大学数学与大数据学院硕士研究生;赵前进(1967—),男,安徽凤阳人,安徽理工大学数学与大数据学院教授,工学博士,硕士研究生导师,主要从事有理插值与逼近、数字图像处理研究。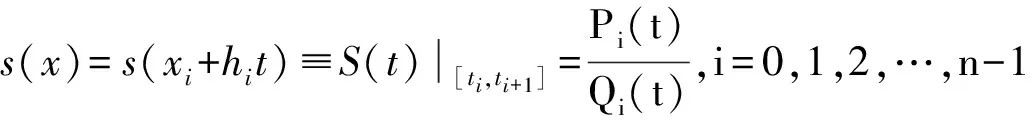
2 保单调性分析[4-8]

3 有理四次样条插值函数二阶连续


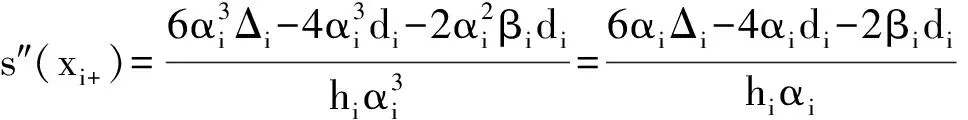
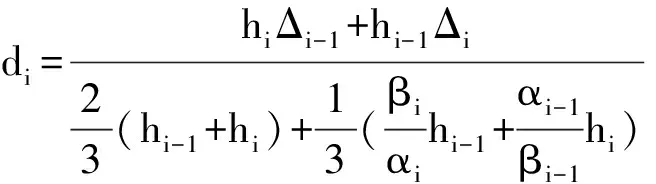
4 插值曲线的应变能


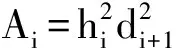


5 应变能最小的保形有理四次样条插值曲线


6 数值例子


