热解用水平管气力输送底层速率的阵列检测研究

吴 煜，司 慧

(北京林业大学工学院，北京 100083)



研究与设计

热解用水平管气力输送底层速率的阵列检测研究

吴 煜，司 慧*

(北京林业大学工学院，北京 100083)

为检测热解用水平管气力输送底层颗粒速率，以落叶松锯末颗粒为物料，基于牛顿第二定律，采用阵列分层检测方法，在自主设计搭建的试验台上考察了电磁阀占空比对底层颗粒进料率、平均速率、质速积等的影响。结果表明：落叶松锯末颗粒之间的空气间隙有益于促进落叶松锯末颗粒的流动；随着占空比的增加，进料率减小，输送质量提高。当管路轴线距参考面高度为0 mm时，底层颗粒平均速率v为0.13～0.16 m/s；在等占空比的情况下，周期越长，总质速积越趋于稳定(±0.2 g·m/s)，底层颗粒质量占总输送质量的比例越小，该比值范围为31%～39%。

热解；气力输送；落叶松锯末；阵列检测；速率

快速热解技术是生物质高值化利用领域的热点技术之一[1]，气力输送是一种比较常用的传统进料方法，但在热解领域中应用它有一定难度，反应器的温度、压力、稳定性等特殊工艺导致气力输送存在反喷、炭化、堵塞等问题[2-5]。

落叶松锯末是一种可高值化利用的热解原料，其在气力输送的进程中固气比例较低，属于稀相输送[6-7]。在热解进料温度条件下，颗粒容易软化、干燥、炭化[8-10]。停机时，热解气易冷凝析出热解液[11]。热解液容易粘附在颗粒上，使管路底层颗粒结块并粘附于管壁，通过增加输送压力或增加气体质量流量可使管路变得通畅[12-13]。气力输送时，管路底层的质量流量和密度通常高于顶层，底层颗粒的运动速率通常低于顶层[14]。相对而言，位于管路内底层的颗粒输送时间最长，加热程度最严重，因此，对底层颗粒进料率、平均速率等参数的监测及其工作机理的研究能够更有效地预测颗粒受热时间(即输送时间)，避免由于颗粒过于干燥导致的炭化或结块。管路颗粒速率检测方法主要分为介入式检测和非介入式检测两种，其中非介入式检测在检测过程中能够避免对进料的干扰，应用比较广泛[15-18]。

为检测水平管底层颗粒的输送速率，本文采用阵列式区域收集统计的方式，根据单颗粒运动满足的牛顿第二定律进行推理[19-20]，在自主设计搭建的气力输送试验台上进行底层颗粒速率检测试验，着重考察了单周期电磁阀占空比对底层颗粒速率的影响。其中“占空比”表示单周期电磁阀打开时间与周期时间的百分比，“质速积”表示多个颗粒质量与速率的乘积之和。

1 试验装置及原料

1.1 试验装置

试验装置主要由料斗、喷嘴、电磁阀、风机、进料管、51单片机、阵列式收集器，以及电源线路等组成，如图1所示。采用ACO-002型风机(35 W、50 Hz、40 L/min，0.02 MPa)压缩空气，压缩空气在电磁阀的控制下通过喷嘴进入水平管(DN 10 mm的304不锈钢管)，同时将从料斗(304不锈钢，75°倾斜角)中下落的物料输送至阵列式收集器(35 mm×35 mm方格构成基元，形成5 mm×10 mm阵列排列，由硬质卡纸搭建的基元构成)，并通过电子天平(JM 1000、1000 kg/0.01 g，余姚市纪铭称重校验设备有限公司生产)分别采集各模块质量参数。电磁阀频率通过90C51单片机(普中科技)和5 V转24 V功率放大电路实现编程调控。出料口至料斗轴线距离为350 mm；喷嘴管口与料斗轴线的距离为30 mm；管道底部至阵列式收集器顶面的高度为65 mm。

图1 试验装置1.电源；2.51单片机；3.风机；4.电磁阀；5.喷嘴；6.料斗；7.水平管；8.电子天平；9.阵列式分布收集器

1.2 试验原料

试验原料为东北小兴安岭林厂提供的落叶松锯末(2014年2月生产)，通过细滤网筛分得到约0.45～0.6 mm粒径的颗粒。锯末颗粒在输送过程中容易与塑料(如PVC管)摩擦产生静电，使颗粒吸附在PVC、橡胶及玻璃等材料上，降低颗粒的流动性。本试验采用了304不锈钢管，以避免产生静电的问题。

1.3 试验方案

搭建进料试验台，对物料的物理特性进行分析，以掌握物料的密度、含水率、颗粒分布等特性。按实验组1～9进行底层颗粒临界速率的检测试验，以确定占空比对颗粒分布、底层颗粒进料率、平均速率、质速比等的影响。实验组的单周期电磁阀开闭时间及占空比见表1。

表1 实验组单周期电磁阀开闭时间及占空比

2 底层颗粒速率检测

2.1 落叶松锯末特性分析

使用自然堆积密度测量仪(SK-1003，Qun Long)测试颗粒的堆积密度、振实密度和休止角，使用含水率测量仪器(顺达科)测量落叶松锯末颗粒的含水率，落叶松锯末特性见表2。该原料振动后密度急剧增加，振实密度和堆积密度为近两倍的关系，这可能是锯末颗粒具有很强的黏结性所致[21]。

表2 落叶松锯末特性

2.2 管路底层颗粒速率分解

单颗粒在管口截面的速度分解模型如图2所示。水平管口截面颗粒的速率分布间接反应了输送的状态。单颗粒速度方向为沿轨迹的切向方向，其沿x、y、z轴分解后可得Vx，Vy和Vz三个方向的分速度。在重力作用下，Vz对平抛运动的影响主要表现为改变颗粒在空气中的运动时间，因此三维速率分布可简化为Vx和Vy组成的二维平面速率分布。预试验发现颗粒离开管口后在平面堆积的效果与截面状态有关，根据牛顿第二定律，单颗粒平抛或斜抛运动水平方向不再受力时将保持匀速运动。气体离开管口后在一定的距离内仍保持原方向运动，对颗粒仍有一定的维持速度的作用。单颗粒运动分区如图3所示。

图2 管口截面单颗粒速度分解模型

图3 单颗粒运动分区

假设颗粒在管口截面仅存在水平方向速率Vx，则颗粒在离开管口截面后的加速效果与离开截面时距离管路底层的高度L(0≤L≤D)紧密相关。管口截面处水平速率为Vx，水平运动距离为s，平抛运动时间为t，重力加速度为g，则颗粒离开截面时距管路底层的高度H与到达阵列式收集器顶面时间t的关系式为：

H=gt2/2

(1)

管口截面处的水平速率为：

Vx=s/t

(2)

考虑到管外持续区的保持速度作用及空气阻力作用，水平输送距离可修正为：

(3)

式中：a为颗粒离开管外持续区后在自由平抛区X(Y)方向的加速度(m/s2)；t1为颗粒在管外持续区的运动时间(s)；根据高度L可得管外区的运动时间为：

(4)

式中：t2为颗粒从管路底部至阵列式收集器顶面的时间(s)，可表示为：

(5)

Vx与气体输送压力和管路输送相态有关[22-23]，实际上颗粒在管口横截面的速度方向是不一致的，在X-Z平面或Y-Z平面上Z方向不同分速度Vz对颗粒的影响都将导致颗粒在空气输送时间和输送距离的变化。在X方向存在输送距离的概率统计离散因子r1，其表示X方向实际输送结果与平均值的偏差。在Y方向输送距离同样存在一个概率统计离散因子r2，其为Y方向实际输送结果与平均值的偏差。因此，距离公式可以调整为：

(6)

(7)

令l=r2，并对r和S微分后可得：

(8)

(9)

颗粒离开管外持续区域后，在自由平抛区域X(Y)方向的加速度a可通过试验测量H=0 mm时的平均速率V间接获得，因此最终可以得到X或Y方向颗粒速率在半径方向的离散分布规律，其可为测量底层颗粒速率提供参考。

3 试验结果与分析

3.1 颗粒分布和分区

阵列式收集器收集的颗粒在X-Y二维平面和三维空间的质量分布如图4所示，二维平面颗粒分区如图5所示。水平管口截面圆心坐标分别是(0，0，70)和(15.75，0，5)。堆积层在X-Y平面投影呈椭圆形，外圈等值线间距均匀但中间越来越密，即堆积角增大；峰值坐标均值分别为(0，15.75)和(15.75，8.75)。将速度相近的颗粒归为一类，在X-Y平面分成5×10类，并假设同类颗粒在圆管截面处于相同位置，且颗粒堆积效果与实际输送状态一致，其分布关系如图5(a)所示。受重力作用，脉冲气力输送底层速率普遍低于均值。

截面不同位置密度和速率不同，颗粒分布大致可以分为顶层(35%～40%)、中间层(25%～30%)和底层(35%～40%)，如图5(b)所示。由于底层速率低，可基本认为X-Y平面底层颗粒即为在管路底层输送的颗粒。考虑到颗粒Z方向存在分速度干扰颗粒飞行时间，故将底层和顶层质量的百分比基本保持一致，使管路底层颗粒跳跃至顶层区域和管路顶层颗粒跳跃至底层区域的概率一致，从而可忽略Z方向速率对分布的干扰。

(a)X-Y二维平面

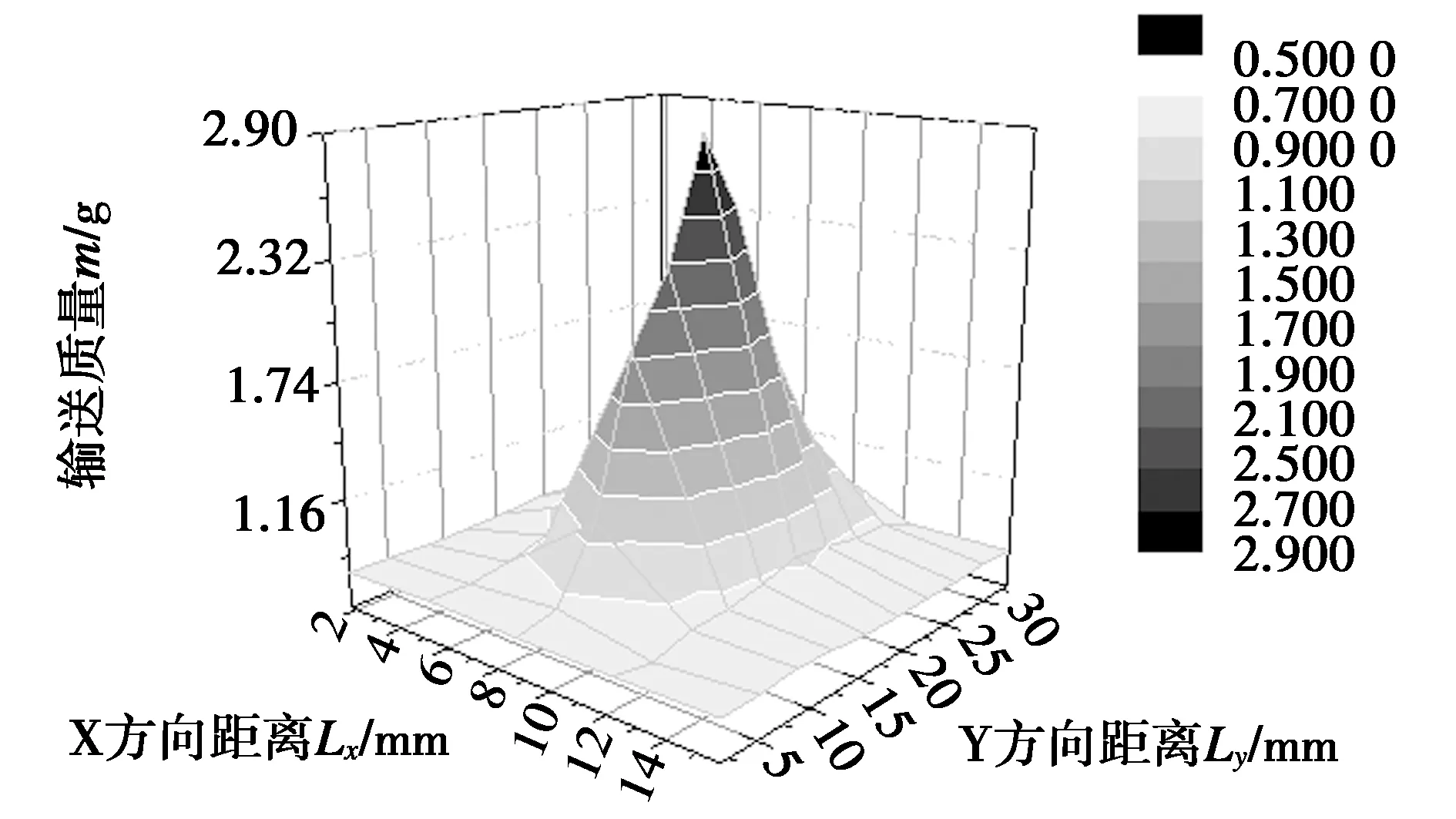
(b)X-Y-Z三维空间(H=65 mm)

(a)圆管截面与阵列式收集器区域微分

(b)圆管截面与堆积颗粒分层

3.2 底层颗粒试验结果分析

试验分别描述了进料率与输送质量、质速积、平均速率、平均加速度等随占空比变化的情况，9个数据点依次对应表1中的实验组序号1～9。其中，实验组1、2、6，3、5、8和4、7、9对应的电磁阀打开时间相等，依次为0.5 s、1 s、1.5 s，且每组的电磁阀关闭时间由1.5 s、1 s、0.5 s依次减小。

3.2.1 进料率与输送质量

进料率f表示单位时间电磁阀打开时的输送质量，其与输送质量m和占空比k有关，计算公式为：

f=m/(60×k)

(10)

进料率与输送质量的关系如图6所示。当阀门打开时间一定时，通过实验组1、2、6，3、5、8和4、7、9的实验情况可知，阀门关闭时间越短进料率越低。在等占空比的情况下，由实验组4、5、6的实验情况可知，阀门开闭周期越长进料率越低，输送质量也越少。当H=65 mm时，进料率与占空比呈负相关，输送质量整体略有增加，与占空比无明显线性关系；当H=0 mm时，进料率整体略有降低，但与占空比无明显线性关系，输送质量与占空比呈正相关。总体而言，随占空比增加，进料率降低，输送质量增加。

3.2.2 输送质量

30 s输送质量与占空比的关系如图7所示。由实验组1、2、6，3、5、8和4、7、9的实验情况可知，当阀门打开时间一定时，阀门关闭时间越短，输送质量越大。底层颗粒质量占总质量的比例与阀门周期无明显线性关系，底层颗粒质量占总质量的比例与占空比也无明显线性关系。该比值范围在31%～39%之间波动，与理论设定范围35%～40% 基本相符。由实验组4、5、6的实验情况可知，在等占空比的情况下，周期越长，该比值越小，同时总输送质量减少，底层颗粒输送质量明显减少。

图7 占空比与输送质量的关系

3.2.3 质速积

质速积表示颗粒的平均动量和。由统计学方法可得到颗粒的总质速积E(或底层颗粒质速积e)的表达式为：

E=∑(区域质量×区域平均速率)

(11)

质速积与占空比的关系如图8所示。由实验组1、2、6，3、5、8和4、7、9的实验情况可知，当阀门打开时间一定时，阀门关闭时间越短，总质速积和底层颗粒质速积越大。当H=65 mm时，随着占空比的增加，质速积趋于基本稳定(±0.1 g·m/s)；当H=0 mm时，随着占空比的增加，颗粒总质速积不断增加而底层质速积浮动较大。由实验组4、5、6的实验情况可知，在等占空比的情况下，阀门周期越长，总质速积越趋于稳定(±0.2 g·m/s)。

图8 质速积与占空比的关系

3.2.4 平均速率

颗粒整体平均速率V(或底层颗粒平均速率v)可由下式得到：

V=E/m

(12)

颗粒速率与占空比的关系如图9所示。由图9及实验组1、2、6，3、5、8和4、7、9的实验情况可知，当阀门打开时间一定时，阀门关闭时间越短，平均速率和底层颗粒速率越趋于保持不变。底层颗粒平均速率低于平均速率，且H越大，底层颗粒平均速率越低。由实验组4、5、6的实验情况可知，在等占空比的情况下，当H=65 mm时，平均速率和底层颗粒平均速率基本稳定(±0.02 m/s)；当H=0 mm时，阀门周期越短，平均速率和底层颗粒平均速率越低，分别为0.27～0.33 m/s和0.13～0.16 m/s。当输送压力和流量一定时，在管路内短距离时底层颗粒可视为匀速，停留时间可由下式估算：

T=L/E

(13)

式中：L为管路长度，L=350 mm。底层颗粒在管内输送时间约为T=(2.19～2.69)s，可据此进一步考察颗粒在该时间内的加热程度，从而避免由于颗粒软化而堵塞管路。

图9 颗粒速率与占空比的关系

3.2.5 加速度

由于空气阻力、颗粒间作用力等因素的影响，落叶松锯末颗粒平抛过程减速明显。在X或Y方向，颗粒平均加速度a(或底层颗粒加速度ad)的表达式为：

α=ΔV/t2

(14)

平抛过程颗粒加速度与占空比的关系如图10所示，颗粒平均加速度为-1.49 m/s2，颗粒底层平均加速度为-0.52 m/s2。颗粒速率越大，加速度绝对值越大，减速越快。

图10 加速率与占空比的关系

4 结论

(1)落叶松锯末颗粒间的空气间隙有益于促进颗粒的流动。

(2)当阀门打开时间一定时，阀门关闭时间越短，输送质量越大，进料率越低，总质速积和底层颗粒质速积越高，平均速率和底层颗粒速率基本保持不变，底层颗粒平均速率低于平均速率。

(3)在等占空比的情况下，周期越长，总输送质量越小，底层颗粒输送质量明显降低，总质速积基本稳定(±0.2 g·m/s)；周期越长，底层颗粒质量占总输送质量的比例越小，该比值范围在31%～39%之间。

(4)随着占空比的增加，进料率降低，输送质量增加，质速积的变化与高度H相关。

(5)底层颗粒平均速率约为0.13～0.16 m/s，可据此进一步考察颗粒在该时间内的加热程度，从而避免由于颗粒软化而堵塞管路。

[1] Berruti F M，Briens C L.Novel intermittent solid slug feeder for fast pyrolysis reactors；Fundamentals and modeling[J].Powder Technology，2013，47(7)：95-105.

[2] 许盼，陈晓平，梁财，等.生物质高压密相输送特性试验研究[J].工程热物理学报，2012，33(5)：801-804.

[3] 王述洋，牛海峰，王九龙.生物质制油粉料气流输送与干燥装置的理论研究[J].安徽农业科学，2014，9(1)：303-305.

[4] 任学勇，王文亮，司慧，等.生物质定向热裂解液化装置的开发Ⅱ：进料特性与流化规律[J].木材加工机械，2012，29(4)：15-18.

[5] 程琦，司慧，王霄.生物质热解用气动进料器的进料特性研究[J].林业机械与木工设备，2016，44(5)：20-24.

[6] 高敬国，徐德龙，赵江平.粉体密相气力输送理论与技术进展[J].中国粉体技术，1999，6(5)：35-37.

[7] Ji D，Gao M，Yu F，et al.Conversion of sawdust to bio-fuels by pyrolysis within molten sodium hydroxide[Z].IEEE，2012：212-216.

[8] 吕薇，孙宏伟，李瑞扬，等.生物质燃料气流干燥的数值模拟与试验研究[J].青岛科技大学学报：自然科学版，2011，32(2)：185-189.

[9] 王霄，司慧，程琦.环形流化床生物质热裂解反应器的传热分析[J].科技导报，2013，31(14)：30-34.

[10] 林肖庆，吕豪豪，刘玉学，等.生物质原料及炭化温度对生物炭产率与性质的影响[J].浙江农业学报，2016，28(7)：1216-1223.

[11] 任学勇，王鹏起，常建民，等.林木剩余物快速热裂解液化技术探析及展望[J].林业机械与木工设备，2008，25(9)：13-16.

[12] Mittal A，Mallick S S，Wypych P W.An investigation into flow mode transition and pressure fluctuations for fluidized dense-phase pneumatic conveying of fine powders[J].Particuology，2014，7(5)：187-195.

[13] Hu S，Zhou F，Geng F，et al.Investigation on blockage boundary condition of dense-phase pneumatic conveying in bending slits[J].Powder Technology，2014，48(6)：96-105.

[14] Chen W，Williams K C，Jabs I，et al.A qualitative study on the pulsatile flow phenomenon in a dense fly ash pneumatic conveyor[J].Particuology，2014，7(17)：81-91.

[15] Middha P，Balakin B V，Leirvaag L，et al.PEPT-A novel tool for investigation of pneumatic conveying[J].Powder Technology，2013，47(7)：87-96.

[16] Lecreps I，Orozovic O，Erden T，et al.Physical mechanisms involved in slug transport and pipe blockage during horizontal pneumatic conveying[J].Powder Technology，2014，48(2)：82-95.

[17] Zhang X，Zhang D，Wang A，et al.Transportation characteristics of gas-solid two-phase flow in a long-distance pipeline[J].Particuology，2015，8(21)：196-202.

[18] Qian X，Yan Y，Wang L，et al.An integrated multi-channel electrostatic sensing and digital imaging system for the on-line measurement of biomass-coal particles in fuel injection pipelines[J].Fuel，2015，45(1)：2-10.

[19] 赵云华，刘文铁，沈志恒，等.LES-DSMC方法研究超细颗粒气固两相流动过程[J].工程热物理学报，2006，27(5)：805-807.

[20] 王伟文，周忠涛，陈光辉，等.流态化过程模拟的研究进展[J].化工进展，2011，30(1)：58-65.

[21] Berruti F M，Ferrante L，Berruti F，et al.Optimization of an Intermittent Slug Injection System for Sawdust Biomass Pyrolysis[J].International Journal of Chemical Reactor Engineering，2009，7(1)：1-25.

[22] Setia G，Mallick S S，Wypych P W.On improving solid friction factor modeling for fluidized dense-phase pneumatic conveying systems[J].Powder Technology，2014，48(7)：88-103.

[23] 张燕，佟达，宋魁彦.生物质能的热化学转化技术[J].森林工程，2012，28(2)：14-17.

(责任编辑 张雅芳)

Study on Array Stratified Testing of Horizontal Tube Bottom ParticleVelocity in Pyrolytic Pneumatic Conveying

WU Yu，SI Hui*

(School of Technology，Beijing Forestry University，Beijing 100083，China)

In order to test the velocity of horizontal tube bottom particles in pyrolytic pneumatic conveying，a test adopting the Larch saw dust as conveying materials and using array stratified collection method based on Newton’s second law is performed.An independently designed test bench is used and the effects of duty cycle of solenoid valves on the feeding rate，average velocity and the product of the quality and velocity of horizontal tube bottom particles are investigated.The results show that the air gap between the particles is conducive to promoting the flow of Larch saw dust.With the increase in duty cycle，the feeding rate decreases and the feeding quality increases.The average velocity of bottom particles is from 0.13 m/s to 0.16 m/s when the height from the pipe axis to the reference plane is 0 mm.When the duty cycle is constant，with the increase of periodic time，the product of the quality and velocity keeps stable(±0.2 g·m/s)and proportion of the quality of particles in the tube bottom in the feeding quality decreases，with the proportion value ranging from 31% to 39%.

pyrolysis；pneumatic convey；Larch saw dust；array stratified testing；velocity

2017-04-10

北京市科技计划课题项目(Z161100001316004)

吴 煜(1990-)，男，硕士研究生，研究方向为生物质热解气力输送进料技术，E-mail：wuyu582932445@sina.com。

*通讯作者：司 慧(1957-)，女，教授，博士生导师，研究方向为生物质热解技术，E-mail：sihui@bjfu.edu.cn。