蔡氏混沌电路综合设计性实验

薛 雪， 刘晓文， 陈桂真， 梁 睿

(1. 中国矿业大学 信息与控制工程学院， 江苏 徐州 221116；2. 中国矿业大学 电气与动力工程学院， 江苏 徐州 221116)

蔡氏混沌电路综合设计性实验

薛 雪1， 刘晓文1， 陈桂真2， 梁 睿2

(1. 中国矿业大学 信息与控制工程学院， 江苏 徐州 221116；2. 中国矿业大学 电气与动力工程学院， 江苏 徐州 221116)

对电路实验课程进行教学改革，设计了综合设计性实验——蔡氏混沌电路。在阐述蔡氏混沌电路原理的基础上，通过PSpice软件进行仿真，观测到了丰富的混沌行为。为了克服实际电感内阻的影响，设计了不含内阻的有源模拟电感，并给出了实验参考电路，分析和讨论了实验结果。实践证明，该实验从理论分析到软件仿真，从基本电路设计到具体实现，培养了学生的工程意识，激发了学生学习兴趣和创新精神。

电路实验； 设计性实验； 蔡氏混沌电路； 有源模拟电感

工程专业认证能够有效对工程教育专业的教学内容、教学目标进行规范和引导，强调对学生的技术创新及工程实践能力的培养[1]。在工程专业认证的背景下，中国矿业大学电路教学课程组一直致力于电路课程的教学改革，在教学实践中始终注重学生工程意识及工程思维的培养。

电路实验课程是电气工程及其自动化专业一门重要的专业基础课，是本科生第一次接触本专业，塑造工程思想、解决实际问题的实验课程。因此，除了要求学生掌握一些基本的实验技能以外，电路实验课程还适当地增加了一些具有综合性和设计性的实验内容，使之具有工程情境下应用特征，既丰富了教学的形式和内容体系，又激发了学生的创新思维。

在此背景下，本文探讨了蔡氏混沌电路综合实验设计方案，该方案与必修实验中的负阻抗变换器、回转器相结合。通过此综合实验，不仅帮助学生理解理论课上非线性电路的基础知识、更加牢固掌握仿真软件PSpice的使用，而且让学生理解混沌现象的应用。从理论分析到软件仿真，从基本电路设计到具体实现，将工程观念渗入到实验的每个环节，培养了学生自主获取知识的能力，激发了学生学习兴趣和创新精神。

1 蔡氏混沌电路的工作原理

1.1 蔡氏混沌电路

如图1所示，蔡氏混沌电路是一个三阶非线性自治电路[2-3]，它由电阻、电感、电容和一个分段线性电阻组成，电阻R、电感L、电容C1与C2组成线性部分，只由一个分段线性电阻RN组成非线性部分，分段线性电阻RN也就是有源非线性负阻元件[4]。其中电感L和电容C2组成振荡回路，其损耗可以忽略；电阻R和电容C1串联，移相输出振荡产生的正弦信号。

图1 蔡氏混沌电路

1.2 有源非线性电阻的实现

有源非线性电阻RN是蔡氏混沌电路中的一个重要元件，由2个负阻并联而成，电路见图2。

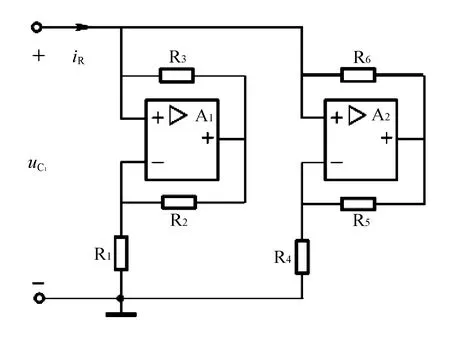
图2 有源非线性电阻电路

如果计及运放工作在饱和区的情况，结合必做实验——负阻抗变换器的理论知识[5]，可以得到其端口的u-i特性曲线有5段曲线，如图3所示[6]。将混沌电路工作在其中的三段负阻折线区，便可实现其分段线性的负电阻RN。其中有：

式中,Ga为内侧斜率，Gb为外侧斜率。

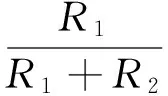
Usat为运放的饱和值。

Ga=Ga1+Ga2，Gb=Gb1+Ga2，Gc=Gb1+Gb2

图3 有源非线性电阻特性曲线

1.3 蔡氏混沌电路的实现

对于图1所示的蔡氏混沌电路，由基尔霍夫定律，可得电路的状态方程为：

(1)

其中，由于RN的非线性负阻特性，因此f(uc1)是一个三段线性的分段函数，其函数形式为

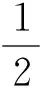
(2)

求解此状态方程，发现其相空间轨迹具有双漩涡结构。改变电路中R的大小，电路会首先工作于周期1、周期2、周期3等各种周期；然后随着R的持续减小，会先出现单涡卷混沌，再出现双涡卷混沌。

2 蔡氏混沌电路的PSpice仿真研究

利用PSpice软件搭建的蔡氏电路[7]见图4。选取参数C1=10 nF，C2=100 nF，L=18.68 mH，R为系统的可调参量。运放为LM324，工作电压为±15 V，R1=2.4 kΩ，R2=R3=220 Ω，R4=3.3 kΩ，R5=R6=39 kΩ。非线性负阻RN的大小由内侧斜率Ga、外侧斜率Gb以及转折点E1和E2这几个参数决定。通过计算可以得出图4中的Ga、Gb以及E1、E2如下：

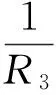
设第一个负阻的转折电压为1V

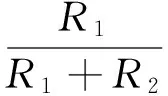
得到Usat≈7.67 V。

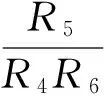
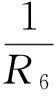
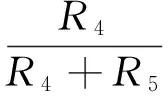
即第二个负阻的转折电压为6.91V。

图4 蔡氏电路的仿真电路

蔡氏二极管的伏安特性仿真结果如图5所示，通过观察R两端电压uC1和输入电流iR之间的关系，可以得到蔡氏二极管伏安关系呈负阻特性，这与理论计算及图3曲线是一致的。

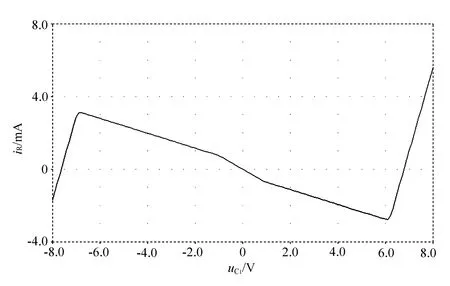
图5 蔡氏二极管的伏安特性曲线

保证电路其他参数不变，只改变R的阻值，观测uc2的时域图与蔡氏电路uc1-uc2相图，如图6所示。发现当R值变化时，电路展示出了丰富的混沌行为。在改变R的过程中，可以观察到蔡氏电路出现分岔。分岔是指在系统中，当某个参数越过临界值时系统长期行为的突然变化，在相空间表现为周期的倍增效应。分岔的最终结果就是形成混沌。当电阻R从2 050 Ω开始减小时，蔡氏电路分别经过稳定的焦点临界、周期1、周期2、单涡卷混沌和双涡卷混沌，呈现了丰富的混沌状态。其中，图6(e)的相图轨线围绕着两个焦点交叉环绕，是一种双涡旋混沌吸引子，电路的动力学行为呈现出混沌。双涡旋混沌吸引子是奇怪吸引子，是混沌研究的焦点之一[8-11]。

3 基于有源模拟电感的蔡氏电路设计与实现

3.1 有源模拟电感的实现

事实上，在实际的蔡氏电路中，电感的参数不仅很难得到准确控制，而且非常容易受到频率、环境等各种因素的影响。一般来说，电感的内阻会对振荡电路造成影响，而且电感的值越大，电感内阻也就越大，同时其对电路的影响也就越大。为了将电感内阻对电路的影响降到最低，可以在实验中将实际的电感用模拟电感代替，该模拟电感可以等效为没有内阻消耗的理想电感[12-13]。为此，结合电路实验中原有的必做实验，采用了回转器电路来实现模拟电感，电路见图7。

根据运算放大器的特性，可以得到该电路 输入阻抗运算形式为

Zin(s)=U(s)/I(s)=Z1Z3Z5/(Z2Z4)

(3)

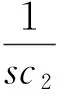
Leq=R1R3R5C2/R4

(4)

图6 蔡氏电路的仿真结果图

图7 回转器实现模拟电感电路

从式(4)中可以看到，改变式中任意一个电容值或者电阻值，模拟电感的数值都会发生改变，从而获得需要的电感值。但是要注意，模拟电感数值仅是非线性电路中的一项指标，为了保证模拟电感在特定电路中的正常工作，还需要设计不同的动态范围，来满足各种非线性电路的要求。

模拟电感的动态范围与非线性电阻元件特性的有效区域的协调问题是电路设计的关键，也就是说模拟电感代替混沌电路里的理想电感工作时，原混沌电路的非线性动态行为并不会受到影响。为了使模拟电感一直工作在线性区域，必须确保模拟电感两端的电压峰值:Ud≤Usat/2 (Usat为运放的饱和电压)。由图5计算得到，Usat≈7.67 V，而模拟电感两端的电压峰值Ud≈1.1 V，满足Ud≤Usat/2，所以可以得出上述模拟电感是工作在线性区域的，因此可以代替理想电感元件。根据上述的分析还可以得出，蔡氏电路中的非线性电阻元件RN工作在图4电路中的3段负阻折线区，因此RN的两端电压必须在转折点-E2和E2之间。E2=6.91 V，而RN两端的电压∣Uc1∣≤6.0 V，所以完全满足要求。

3.2 基于有源模拟电感的蔡氏电路的实现

将蔡氏电路中的理想电感元件用有源模拟电感代替进行仿真，其PSpice电路见图8。各元器件选择如下：R1—R6参数不变，C1=10.25 nF，C2=100 nF，C3=0.233 μF。运算放大器仍选用LM324，以R7作为连续可调电阻。

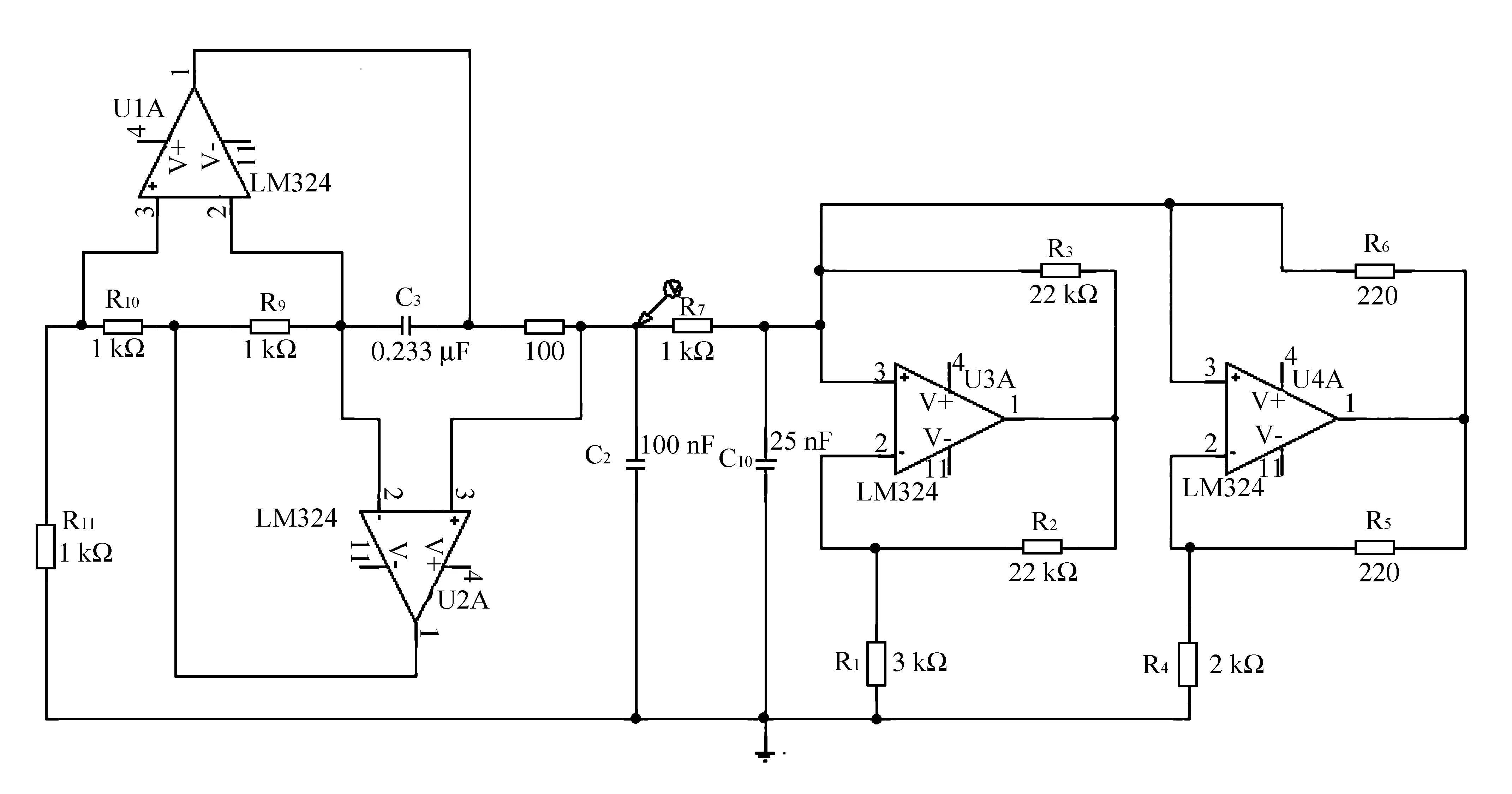
图8 基于模拟电感的蔡氏电路的PSpice电路

图8电路仿真结果如图9所示。当R7从2 057Ω开始逐渐减小时，系统首先经过周期1、周期2、周期3，…，然后逐渐出现其他各种周期。随着R7的持续减小，会先出现单涡卷混沌，然后出现双涡卷混沌。表现出来的非线性现象与图6基本相同，说明模拟电感实现集成化混沌信号发生器的方法是可行的。

根据最后的仿真结果，可以得到基于模拟电感的蔡氏电路比实际电感性能更加优越如下：

(1) 易振荡：将模拟电感用在振荡电路中，电路特别容易振荡，图9中R7=2 057 Ω时，电路就发生了振荡，而图6中R=2 007 Ω时，电路才发生振荡。因为实际电感有内阻，当内阻较大时，振荡电路难以起振，采用模拟电感可以克服实际电感有阻耗的缺陷。

(2) 易调整：要想得到多种多样的混沌现象，可以根据需要保持蔡氏电路中其他参数不变，只要改变模拟电感内部任意R或C的值，而且可调电阻R7的变化范围大(2 057～1 663 Ω)，给实际研究带来方便。

(3) 易集成化：模拟电感通过集成运放来实现，使得整个电路更易于集成化。

4 结语

从2012年电气工程及其自动化专业申请工程认证试点开始，电路实验学时数就改为32学时。其中，设置的最后4学时是实用电路设计，属于综合设计性实验。该实验完全放开限制，从开始时的实验选题到结束时的实验报告全部交给学生独立完成。要求学生2～3人一组，自由组合，自行查阅相关资料，研究实验原理，确定实验方案。本文设计的蔡氏混沌电路只是若干可选题目中的一个，要求学生善于利用各种资源，充分发挥主观能动性。首先查阅资料，学习工作原理，然后设计参数，运用仿真软件设计电路，到最后的总结分析。

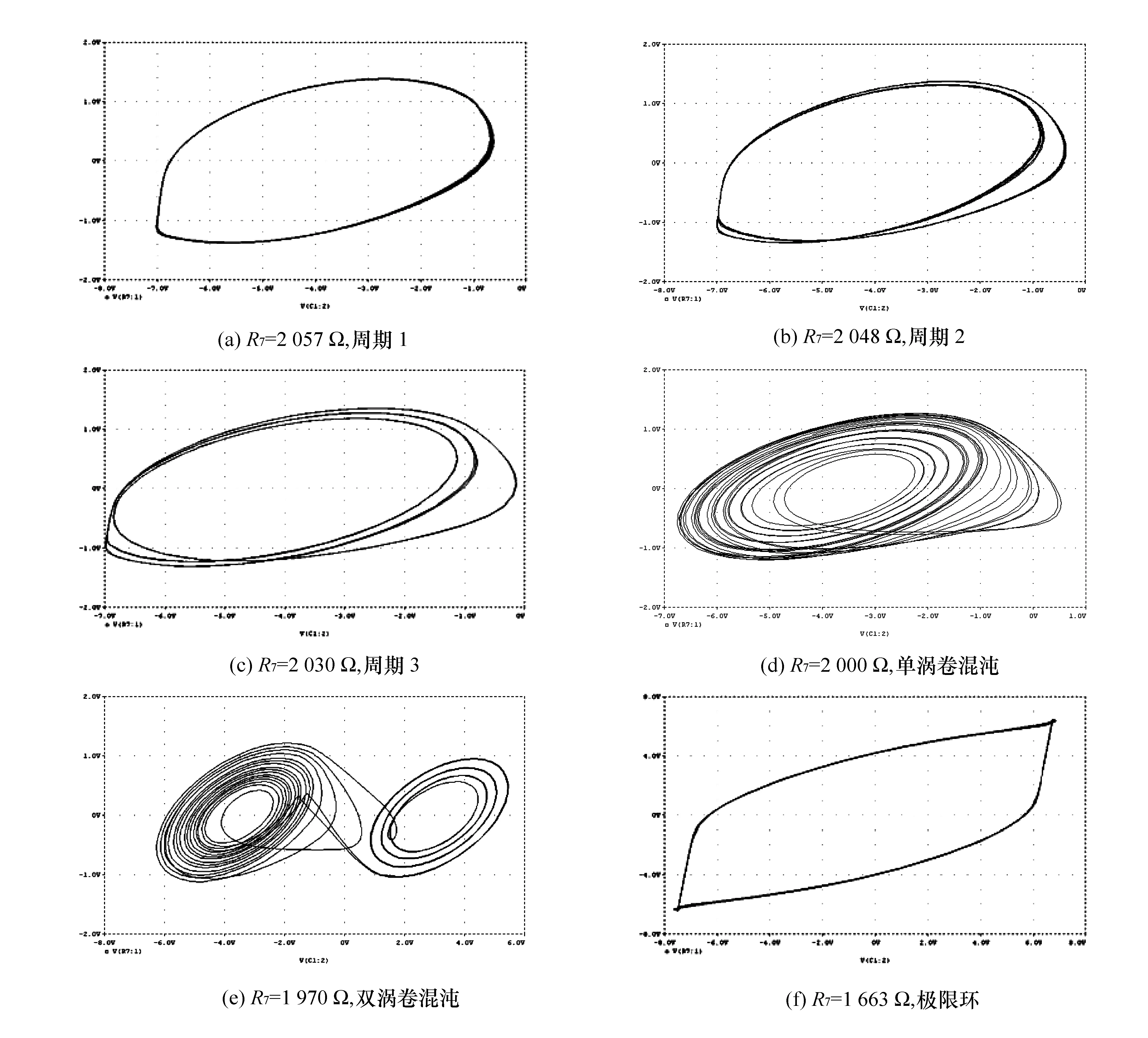
图9 基于模拟电感的蔡氏电路周期与混沌相图

从最近两届学生的实验来看，选做这个实验的学生大概占到10%左右，做过的学生都感触颇深，通过PSpice仿真，可以对简单电路中复杂的非线性运动有一个较为直观的了解。学生在做完蔡氏电路的仿真实验后，可以根据自己的爱好适当的做一些拓展，如超混沌电路、蔡氏电路混沌同步的仿真模拟。超混沌电路不同于蔡氏混沌电路，但同样也可以观察到倍周期分岔和吸引子。混沌同步则是混沌保密通信的基础，混沌电路的一个重要应用就是利用蔡氏电路的混沌同步来实现保密通信。混沌电路仿真实验的目的不单是简单的让学生对混沌电路的基本原理和基础知识有一些初步了解，更重要的是让学生通过实验学习一些混沌电路的应用价值。在进行该综合设计性实验的过程中，不仅学生独立思考、自主学习、亲自动手的科研素质得到了培养，而且学生的创新意识和独立解决工程问题的能力也得到了极大的增强，这为学生后续学习专业课程以及从事工程技术打下了坚实的基础。

References)

[1] 戴益民，李浔，张跃飞，等．专业认证背景下化工原理实验工程素质的培养[J]．化工高等教育，2013(4):39-41.

[2] 刘洪臣，孙立山．混沌电路的创新综合性实验的设计与实现[J]．电气电子教学学报，2011，33(3):70-72.

[3] 赵凡，汤剑锋．非线性电路的MapleSim仿真实验[J]．中国教育技术装备，2014(4):114-116.

[4] 邱关源．电路[M]．北京：高等教育出版社，2006.

[5] 刘晓文，陈桂真，薛雪．电路实验[M]．北京：机械工业出版社，2016.

[6] 王殿学．蔡氏电路中混沌现象与非线性电阻伏安曲线关系的研究[J]．辽东学院学报，2010，17(4):317-320.

[7] 夏江涛，肖韶荣，孙冬娇．PSpice在工科电类专业教学中的应用[J]．实验技术与管理，2010，27(12):121-124.

[8] 黄苏华，肖文波，赖相霖，等．仿真蔡氏电路混沌效应的讨论[J]．实验室研究与探索，2012，31(4):76-78.

[9] 邵书义，闵富红，王恩荣．四阶蔡氏电路的数值仿真分析与电路实现[J]．南京师范大学学报(工程技术版)，2012，12(3):6-9．

[10] 杜军，王婷婷，陈新来，等．基于Mutisim的蔡氏混沌序列仿真研究[J]．通信技术，2010，43(4)：84-86.

[11] 钟双英，刘崧，戚小平，等．蔡氏电路混沌控制与同步实验研究[J]. 实验技术与管理，2012，29(11):32-34.

[12] 吴本科，肖苏，谢莉莎．蔡氏电路中电感阻耗对混沌现象的影响[J]．现代电子技术，2005(10):97-99.

[13] 陈立宏，陈莉，高龙．改进蔡氏混沌电路的实现[J]．物理实验，2009，29(6):35-37.

Comprehensive designing experiment of Chua’s chaotic circuit

Xue Xue1, Liu Xiaowen1, Chen Guizhen2, Liang Rui2

(1. School of Information and Control Engineering, China University of Mining and Technology, Xuzhou 221116, China; 2. School of Electrical and Power Engineering, China University of Mining and Technology, Xuzhou 221116, China)

The reform is carried out for the Circuit Experiment course and the comprehensive experiment of Chua’s chaotic circuit is designed. The rich chaotic behavior is observed through the PSpice software simulation. In order to overcome the influence of actual inductance resistance, the active stimulated inductor without resistance is designed, the experimental reference circuit is presented, and the experimental results are analyzed and discussed. The practice has proved that from the theoretical analysis to the software simulation and from the basic circuit design to the concrete realization, this experiment can help cultivate students’ engineering consciousness and stimulate their learning interest and innovative spirit.

circuit experiment; designing experiment; Chua’s chaotic circuit; active stimulated inductor

10.16791/j.cnki.sjg.2017.06.012

2016-12-08 修改日期：2017-01-12

江苏省高校品牌专业建设工程资助项目(PPZY2015B132)；中国矿业大学教学名师培育工程项目

薛雪(1980—)，女，江苏徐州，博士，副教授，硕士生导师，研究方向为电路与系统

E-mail：cumtxx@126.com

刘晓文(1964—)，女，江苏张家港，博士，教授，博士生导师，研究方向为电路与系统.

E-mail：xwliucumt@126.com

TN710；G642.423

A

1002-4956(2017)06-0044-06