大跨越输电线路β阻尼线空间形态及特性分析
王 宇 汪 峰 刘文军 王 丰
(三峡大学 防灾减灾湖北省重点实验室, 湖北 宜昌 443002)
大跨越输电线路β阻尼线空间形态及特性分析
王 宇 汪 峰 刘文军 王 丰
(三峡大学 防灾减灾湖北省重点实验室, 湖北 宜昌 443002)
β阻尼线是大跨越输电线路重要防振金具,其线形影响微风振动防振效果.利用摄动渐进方法,构建了β阻尼线的空间静态线形模型,推导了β阻尼线微风振动和端部激励下的振动方程.并结合500 kV吉阳大跨越β阻尼线防振方案,运用Matlab软件数值分析了β阻尼线的轴力、花边长度对其振动特性的影响规律.结果表明:β阻尼线的轴力随着花边长度和垂度的增加而逐渐减小;β阻尼线的自振频率受轴力和长度的影响较大;建议β阻尼线的单个花边长度小于5 m,以减小微风振动对β阻尼线振动的影响.
大跨越输电线;β阻尼线; 空间形态; 自振频率
架空大跨越输电线路导线持续受到0.5~10 m/s的风场作用时,输电线背风侧会形成上下交替的卡门涡激,产生微风振动[1].该振动持续时间长、振动频率高,易引发导线的疲劳断股,尤其在大跨越输电线路中,因档距大、悬挂点高和水域开阔,风向风速,温度等微气象条件的影响,微风振动的影响更加突出[2-3].
目前大跨越输电线路采用的防振装置主要有防振锤、阻尼线和阻尼间隔棒.β阻尼线由于频率响应范围宽、线夹出口处动弯应变较小等优点被广泛应用于大跨越输电线路中.但目前国内外的有关β阻尼线的研究以及实测数据都较少,至今尚未有完整准确的设计计算方法,设计多通过定性分析进行布置[4-5].为了评估大跨越输电线路β阻尼线的耗能特性,提出更加经济有效的防振方案,需要对β阻尼线的空间形态和动力特性做进一步的研究.
本文运用摄动法求解β阻尼线的静态线形,分析其阻尼线花边长度、垂度与轴力之间的关系.假定β阻尼线的振动分为阻尼线风致振动和端部激励下的振动,推导其微风振动方程.分析不同长度、垂度情况时阻尼线的共振频率,并根据500 kV吉阳大跨越的β阻尼线布置方案,运用Matlab软件进行因素分析,为大跨越输电线路β阻尼线防振方案提供参考.
1 β阻尼线空间线形
阻尼线的空间静态线形对输电线路的振动与自身消振特性都有较大影响.实际工程中,往往通过轴力、花边长度和垂度来进行控制.β阻尼线多采用与导线尺寸相近且刚度相对较小的导线,根据设计的垂度和花边长度将β阻尼线压弯,并固定于导线上,其线形如图1所示.
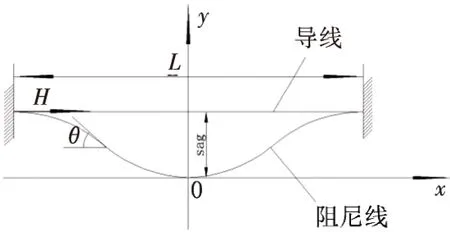
图1 β阻尼线静态线形图
由于β阻尼线档距较短,在计算阻尼线的静态线形时可以忽略其自重的影响,但是必须考虑其两端压力,其变形问题可以近似看作杆的屈曲变形或梁的弯曲问题[3].根据Simpson理论[6],将β阻尼线的线形近似为小刚度梁屈曲问题,屈曲方程为:

(1)
式中,H为β阻尼线的轴向力,EI为阻尼线刚度.
上述方程类似弹性压杆的大变形问题,该方程可以通过椭圆积分求出精确解[7].但椭圆积分使用较为复杂,为了求出显式解,本文采用摄动法渐进求解该方程.由于Y′=tanθ,两端分别对x求导得:
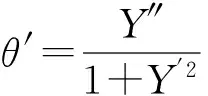
(2)
设Y=Y0ε0+Y1ε1+Y2ε2+Y3ε3+…,H=P0ε0+P1ε1+P2ε2+P3ε3+…,ε=sag/2L,其中L为β阻尼线的档距,sag为β阻尼线的垂度,代入式(2)得:
(3)
对式(3)运用摄动法求解:
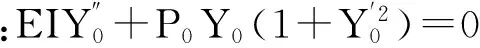
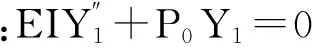
(4)

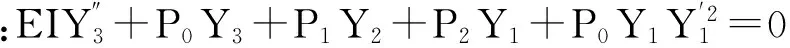
(5)
消去久期项得:
(6)
式(5)变为:
求解得:
(7)
将结果整理后由式(4)、(7)得到β阻尼线的线形:
(8)
由式(4)、(6)得:
(9)
2 阻尼线的振动方程
在稳定的微风激励作用下,阻尼线处于振动状态,导线也时刻将振动传递至阻尼线.为了分析方便,忽略阻尼线的轴向振动,以及轴力在不同位置的变化.假定导线的两端运动状态视作相对运动状态和相对静止的绝对运动状态的叠加.这里绝对运动的状态下阻尼线的振动主要由风激励和一定相对运动产生,本文定义为风致振动;相对运动主要由单个端部激励产生,本文定义为端部激励下的振动.因此,假定β阻尼线的振动分为风致振动和端部激励振动.
2.1β阻尼线的自由振动
β阻尼线的风致振动主要指假设阻尼线两端为固定端部,在风激励作用下阻尼线的振动,如图2所示,β阻尼线的风致振动主要和阻尼线的自振频率有关.

图2 β阻尼线的风致振动形态
β阻尼线自由振动状态可以近似于分布参数体系中梁的弯曲问题[8].其无阻尼自由振动方程为:
(10)
式中,y为阻尼线的空间形态,如式(8)所示;H为阻尼线轴向力;mc为阻尼线单位长度质量.
运用分离变量法求解方程(10).设y=Y(t)·Z(x),代入式(10)并除以Y(t)Z(x),可以得到:
(11)
由式(11)可得:
(12)
(13)

解该常微分方程可得:
(14)
式中,
该方程可以通过边界条件来求解,在边界处β阻尼线的斜率为0,则有:
(15)
(16)
(17)
(18)

(19)
由式(16)(18)可得:d1=-d3,δd2=-εd4,将其代入式(17)、(19)得:
(20)
(21)
设
为使d2,d4不全为0,则其系数矩阵的行列式值应为0,则有Det(A)=0.
化简后得:
(22)
2.2 端部激励引起的振动
β阻尼线在导线振动作用下,可以将边界简化成一端固定,一端有周期性相对位移和转角的模型,如图3所示.

图3 β阻尼线的端部激励
这里将端部的相对位移和转角产生的激励力设为p(x,t),则振动方程化为:
(23)
式中,C为为阻尼系数.
y可以分离变量表示为如下形式:
则端部激励力可化为:
(24)
本文给出端部激励力以及振动方程的表达式,由于该方程在轴力作用下解析涉及到较多复杂问题,本文仅作定性分析.
3 β阻尼线特性分析
为了分析β阻尼线的振动特性及其影响因素,本文以500 kV吉阳大跨越为工程实例.该大跨越档距为1 605 m,采用β阻尼线加防振锤的组合防振体系.输电线路导线采用KTACSR/EST-630/360型号绞线,β阻尼线采用刚度略小的ACSR-720/50导线.该大跨越导线每端的β阻尼线共设14跨花边,花边长度由导线端部向档中依次递减.其中阻尼线的最大花边长度为3.8 m,最小长度为0.9 m.结合公式(8)、(9)和(22),运用Matlab编制计算公式,数值分析β阻尼线的空间线形和振动特性.
3.1β阻尼线静态特性
为了研究β阻尼线的静态特性的影响因素,根据式(8),(9)分别画出β阻尼线不同垂度和花边长度下的空间线形.图4和图5分别为花边长度3.8 m、垂度0.3 m的阻尼线和长度0.9 m、垂度0.1 m的阻尼线.
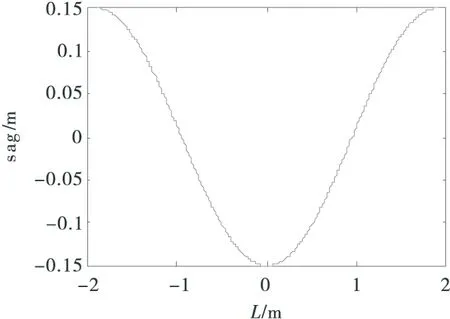
图4 花边长度为3.8 m的β阻尼线线形
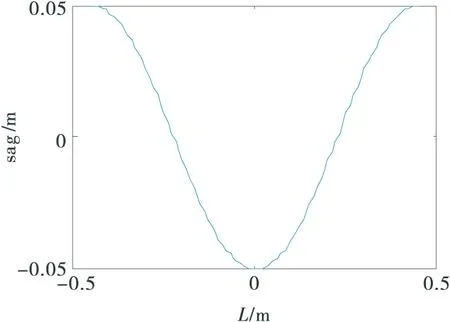
图5 花边长度为0.9 m的β阻尼线线形
由图4和图5可知,β阻尼线每个花边的形状类似,其静态线形类似三角函数和悬链线,该结论可与Clough[8]的静态屈曲线形相印证.阻尼线垂度和花边长度对张力的影响,如图6所示.由图6可知,在一定范围内,β阻尼线的轴力随着花边长度的增加逐渐减少,但当长度较小的情况下,轴力随着档距增加而增加;由500 kV吉阳大跨越可知,0.3 m的垂度对应β阻尼线花边长度为3.8 m,而图6中单调增加段小于1.5 m,远小于实际工况,因此可以认为β阻尼线的轴力随花边长度增加减小.在档距相同的情况下,垂度越大,轴力越小;值得注意的是,这里对比的是长度相同的情况,当β阻尼线长度相同时,该结论应当相反.
图6 花边长度、垂度与阻尼线轴力的关系图
3.2 阻尼线振动影响因素分析
为了分析轴力和花边长度对阻尼线的振动影响,选择了花边长度为3 m,垂度为0.25 m的β阻尼线.由式(22)可以得到阻尼线的轴力与自振频率之间的关系,计算结果如图7所示.

图7 β阻尼线轴力与频率关系图
由图7可知,当β阻尼线的轴力增加时,β阻尼线的各阶频率都呈上升趋势,且轴力越大,频率增加速度越快.
将式(9)代入式(22)中可得到β阻尼线的花边长度与自振频率的关系,如图8所示.
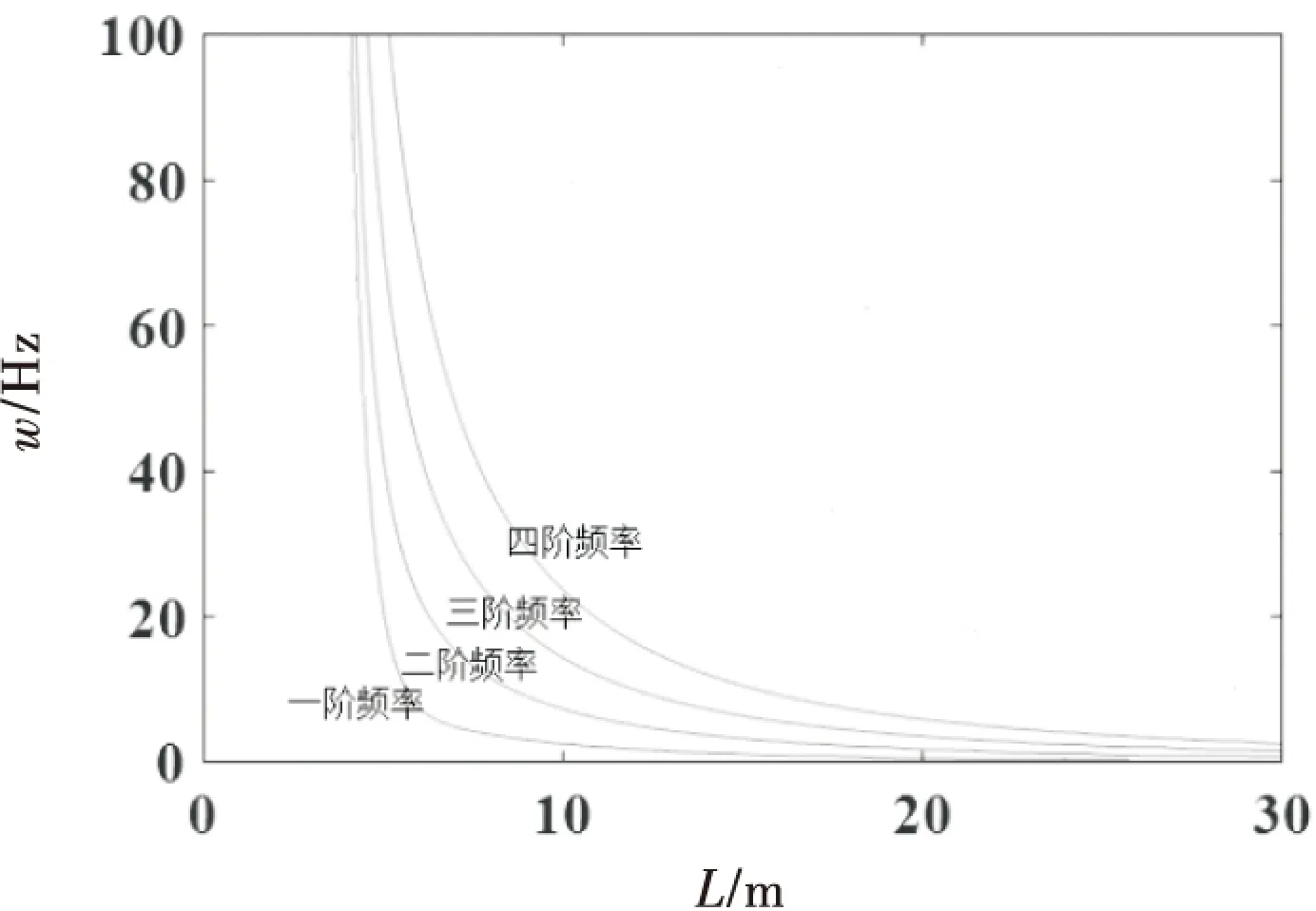
图8 β阻尼线档距与频率关系图
由图8可知,β阻尼线的各阶频率随着每跨花边长度增加而减小,且减少速度较快;当单个花边长度处于1~5 m的范围时,自振频率远超过100 Hz.由风速的近似计算公式:
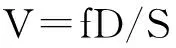
(25)
式中,V为风速;f为频率;D为导线直径;S为斯托克斯常数,取0.2.
通过计算得阻尼线的共振风速已经超过10 m/s,超出了微风振动的范围,所以β阻尼线在1~5 m范围内β阻尼线在相对运动作用下不会产生微风共振,这也是安装β阻尼线后导线的幅频曲线相对安装防振锤较为平滑的原因.
由于β阻尼线在风激励作用下产生的共振会影响导线的防振效果,甚至产生反作用.所以β阻尼线的线长应控制在5 m的范围内,这点也和500 kV吉阳大跨越β阻尼线布置方案相印证.由此可得,β阻尼线防振主要是通过β阻尼线的端部激励产生的振动来消耗能量,起到防振作用.
4 结 论
1)β阻尼线的轴力随着花边长度和垂度的增加而逐渐减小.β阻尼线的自振频率受轴向压力和花边长度的影响较大,轴向压力越大,自振频率越大.
2)在轴力一定的情况下,β阻尼线长度在5 m以内的自振频率都超过了微风振动的激振频率.在实际设计中,β阻尼线应避免发生共振,应当保证阻尼线具有一定的垂度,并保证β阻尼线每个花边长度不超过5 m,以减少风激励对β阻尼线的影响.
3)β阻尼线在端部激励下的振动对抑制导线的微风振动起主要作用,端部激励不仅应包括竖向位移,也应当包括转角作用.
[1] 黄新波,赵 隆,舒 佳,等.输电线路导线微风振动在线监测技术[J].高电压技术,2012,38(8):1863-1870.
[2] 桑 雷.长江镇江段大跨越输电线路微风振动在线监测系统研究[D].北京:华北电力大学,2012.
[3] 李 黎,叶志雄,江宜城,等.β阻尼线的耗能计算及其在输电线防振中的应用[J].振动与冲击,2009,28(8):16-19,196.
[4] 孔德怡,王 鹏,周长征.安装防振锤输电线微风振动试验研究[J].水电能源科学,2011,29(1):151-154.
[5] 邵天晓.架空送电线路的电线力学计算[M].北京:中国电力出版社,2003.
[6] Simpson A,Sembi P S. On the Use of Exact Modal Analysis Techniques in the Design of β Damping Devices for Multi-conductor OverHead Power Lines, Part I: The Control of Aeolian Vibration[J]. Journal of Sound and Vibration,1984,97(3):357-385.
[7] 李银山,刘 波,潘文波,等.弹性压杆的大变形分析[J].河北工业大学学报,2011,40(5):31-35.
[8] Ray Clough, Joseph Penzien. Dynamic of Structures[M]. Computer and Structures,2003.
[责任编辑 张 莉]
Analysis of Spatial Form and Dynamic Characteristic ofβ-Damping Line on Large Span Transmission Line
Wang Yu Wang Feng Liu Wenjun Wang Feng
(Hubei Key Laboratory of Disaster Prevention & Reduction, China Three Gorges Univ., Yichang 443002, China)
It is an important problem to analyze spatial form and vibration characteristics of damping line for large span transmission line. A model of spatial static form of theβ-damping line is constructed by using the asymptotic method. The vibration of theβ-damped line is divided into wind-induced vibration and pedestal-excited vibration by the superposition method. The natural vibration equation of theβ-damping line is solved by using the separation variable method. The influences of axial force and span on the vibration characteristics ofβ- damping line is analyzed by Matlab software. The results show that the axial force ofβ-damping line decreases with the increase of span and sag; the natural vibration frequency ofβ-damping line is greatly affected by axial force and span. The damping line span less than 5 m is suggested to reduce the impact of wind on the vibration ofβ-damping line.
large span transmission line;β-damping line; spatial form; natural frequency
2016-10-20
中国电力工程顾问集团有限公司科研基金项目(DG1-D05-2015)
汪 峰(1979-),男,副教授,博士,主要从事大跨度复杂工程结构非线性计算分析.E-mail:wanggoody@126.com
10.13393/j.cnki.issn.1672-948X.2017.03.016
TM726.3
A
1672-948X(2017)03-0070-05
——垂度法

