谷间软弱土路基稳定性计算方法研究
周 颖 洪宝宁 刘 鑫 甘亮琴 濮仕坤,3
(1. 河海大学 岩土力学与堤坝工程教育部重点实验室, 南京 210098; 2. 河海大学 岩土工程科学研究所, 南京 210098; 3. 解放军理工大学, 南京 210007)
谷间软弱土路基稳定性计算方法研究
周 颖1,2洪宝宁1,2刘 鑫1,2甘亮琴1,2濮仕坤1,2,3
(1. 河海大学 岩土力学与堤坝工程教育部重点实验室, 南京 210098; 2. 河海大学 岩土工程科学研究所, 南京 210098; 3. 解放军理工大学, 南京 210007)
山区谷间路基的稳定性计算,目前仍沿用传统极限平衡的方法,未考虑山谷对路基的约束及谷间软弱土对路基稳定性的影响.依据谷间锅底状软弱土层存在形式,以及邻近山体等对路基稳定性约束的影响,确定了谷间软弱土路基稳定性的特征性描述参数以及修正系数计算方案,并得到了在山体与坡脚的距离和不同软弱土形式下的路基稳定性修正系数计算公式.通过工况对比,发现计算结果与采用本文中提出的稳定性修正系数计算出的安全系数两者相近,论证了本文提出的稳定性修正系数计算公式的可行性.
软弱土; 稳定性; 特征性描述参数; 有限元; 修正系数
随着高速公路建设的迅猛发展,建设区域已逐步从沿海和沿江的经济较发达地区推向山地丘陵较多的经济欠发达地区.考虑到工程造价、施工工期等方面因素,这些高速公路不可避免会有大量穿越山丘地区的软弱土层路段.它们处治形式的选择与处理的效果,将直接影响到整条高速公路的建设造价和工程质量.而仅采用经过平原地区总结出来的设计、施工等理念,山丘地区谷间软弱土路基施工具体应用时会受到严重的挑战.
事实上,工程领域关于高速公路路基土体稳定性方面的研究已经非常广泛和深入,如刘雪岭等[1]、郭进梅等[2]将山区软土路基的破坏形式划分了类型;刘望坤[3]通过鸡爪沟地形路基病害成因分析,对鸡爪沟地形路基的不均匀沉降进行数值计算;王瑞甫等[4]分析了贵州山区斜坡软土的形成条件及形成机制,并计算出了典型滑动面的安全系数;杨兵等[5]认为可以采用塑料排水板加竹排加筋的处理方式处理山区软弱地基;马俊[6]根据山间软土的实践经验,对CFG桩与砂桩的作用机理进行了分析;冯永财[7]利用碎石桩、排水板碎石桩与塑料排水板加固山区软弱路基;崔溦[8]依托赣定高速公路的现场试验,重点研究三种技术处理山区沟谷软基的效果.
可以看出目前针对山丘地区高速公路路基稳定性的研究基本上是围绕集中在山区软土的勘察、病害、处治等方面的研究,而对于其稳定性的分析,较少的针对山丘地区软弱土的工程特性(不同的工程特性指标,将影响稳定安全系数)开展,也未根据山丘地区软弱土的分布形式(条状、锅底状等)建立,导致计算结果往往有较大的偏差.因此,若根据山丘地区软弱土的诸多特点,建立山体稳定性计算的新方法,弥补现有方法的不足,将使计算结果更为准确,并具有更好的可靠性.本文依据软弱土层存在形式(谷间锅底状软弱土层),以及邻近山体等对路基稳定性约束的影响,利用特征性描述参数,通过对比有限元数值模拟计算结果,给出谷间软弱土路基稳定性计算方法.
1 稳定性修正系数确定
1.1 特征性描述参数
由于传统的条分法没有考虑邻近山体与坡脚的距离和软弱土存在形式这两个地形的影响,而这两个参数是山区谷间软弱土路基的两个最为主要的地形特征,由于缺少对它们的考虑,往往使得工程设计人员计算出的路基安全系数与实际情况相差甚远.故将山体与坡脚的距离和软弱土存在形式作为稳定性计算方法的特征性描述参数.
为便于数值模拟计算,进行如下的简化处理:由于大多数的软弱土层呈锅底状,因此可以近似呈椭圆形,其中椭圆圆心为O,长半轴为a,短半轴为b.通过改变椭圆圆心(保持在路基与路基的接触面上)以及长短轴的大小,这样不仅可以模拟不同的锅底状软弱土位置,还可以模拟出软弱土的厚度.例如:将圆心固定在路基中心线,当长半轴a大于路基底部宽度时,可以模拟路基整体位于软弱土层上的情况;当长半轴a小于路基底部宽度时,可以模拟路基整体覆盖软弱土层的情况;改变椭圆圆心的位置,随着圆心往一侧移动,就可以模拟路基局部位于软弱土层上的情况.

图1 软弱土层存在形式的简化
1.2 计算模型
1.2.1 传统Janbu法计算模型及计算结果
由于传统的条分法在计算这种山区谷间软弱土路基的稳定性时,容易忽视地形因素的影响,因此假定当软弱土层厚度为5 m和10 m且为均匀层状分布,不考虑山体的侧向约束作用,分别利用Janbu法和有限元计算稳定性安全系数.为了减小边界条件对于稳定性安全系数的影响,将持力层厚度取为30 m,左侧边界距离坡脚距离为50 m.土层参数见表1,通过计算得到稳定性安全系数见表2:

表1 土层主要物理力学参数表
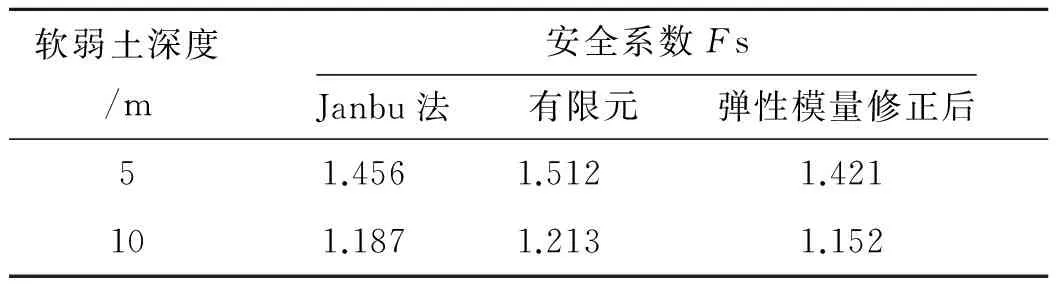
表2 安全系数计算结果
通过试算可以发现,直接采用地勘资料中给出的物理力学指标,有限元计算出的结果比Janbu法计算值偏大.为了保证下文研究的方便以及一致性,而且由于压缩模量在条分法中并没有考虑,因此考虑通过对土层压缩系数的同步折减,使得该工况下的有限元数值模拟结果与Janbu法计算结果保持相同.通过试算发现:当折减系数取0.9时,计算出的结果基本相同.因此本文中方案的计算工况均按修正后的压缩模量取值,见表3.

表3 修正后的压缩模量取值
1.2.2 考虑山体约束的计算模型
选取如图2所示的计算模型,由于整体具有对称性,因此取一半进行分析,路基宽度10 m,高度10 m,路基边坡坡比为1∶1.路基坡脚距离山体距离为S,路基下卧软弱土层,为了简便处理将软土层以外取为均质持力层,持力层左侧为山体,利用有限元软件PLAXIS建模,模型如图3所示.

图2 计算模型图 图3 模型网格划分图
1.3 考虑山体约束的计算方案
下文将通过因素分析法研究两个特征性描述参数:山体距离路基坡脚的距离S和软弱土存在形式对于路基稳定性的影响.
根据前述关于锅底状软弱土路基稳定性的定性分析,以及大量广东省山区的实际工程经验可知:当软弱土层厚度超过6 m,且形式为路基整体位于软弱土层上时,路基的稳定性较差.因此基于危险性考虑,取软弱土层厚度为10 m,形式为路基整体位于软弱土层之上且与路基和山体的交点A重合作为分析形式之一.另外,基于一般情况考虑,取软弱土层厚度为5 m,路基整体位于软弱土层之上或者路基整体覆盖软弱土层上作为另一种重点研究形式.
山体与坡脚距离S的影响分析计算方案见表4.
注:a为长半轴,b为短半轴,L为长半轴的位置,S为山体距离路基坡脚的距离,具体见图2.
2 有限元模拟结果
2.1 山体与坡脚距离S的影响分析
针对方案1、2、3中软弱土层存在形式,对S=0、2、4、6、8、10、15、20、30、40 m的10种工况进行数值模拟,将得到的安全系数值与常规Janbu法计算软弱土层厚度分别为10 m和5 m情况时的结果,即前文计算出的安全系数1.187和1.456的比值进行分析,可以得到安全系数比值曲线如图4所示.

图4 安全系数比值变化拟合曲线图
通过安全系数比值变化曲线可以看出:
1)尽管方案不同,模拟的软弱土深度不同,但是随着山体与坡脚的距离S的增加,安全系数比值总体上呈先增加后减小最后趋于平稳的特点,其中安全系数比值最大点出现在2~4 m处左右.说明并不是侧向约束越大越有利于路基稳定性,通过有限元分析可以发现,当侧向约束很大时,此时的路基失稳一般发生在路基本身,并不穿过软弱土层.
2)由安全系数比值曲线形式可以看出:当山体与坡脚的距离S在4~20 m之间,曲线线性呈抛物线形式.通过线性拟合可以得到相应的二次函数形式,函数表达式见表5.

表5 拟合的安全系数曲线
2.2 修正系数
通过前面的分析可知,传统的Janbu法在计算边坡稳定系数时,不考虑山谷对路基的约束及谷间软弱土对稳定性的影响,即便当有限元计算时对土体参数进行折减,仍然会使得Janbu法的结果偏于保守,因此,有必要对Janbu法谷间软弱土路基稳定性计算进行修正.因此依据山区谷间软弱土两个特征性描述参量,即山体与坡脚的距离S和软弱土层存在形式,基于线性拟合的安全系数比值函数关系,提出山区谷间软弱土修正系数ψFs.
针对方案中软弱土层不同厚度,且椭圆形软土层的长轴与路基和山体的不同交点,给出修正系数公式,见表6.

表6 安全修正系数
由于软弱土存在形式和软土的种类过于繁多,计算时不可能一一罗列.本文主要考虑的是路基坡脚到山谷坡脚之间的距离、理想椭圆形软弱土层长短轴长度这三个参数对路基稳定性的影响.在计算其他工况下的稳定性修正系数时,可考虑使改变土体参数、利用相近地形替代本文山体模型等方法进行处理.
3 计算方法可行性论证
由于前文中给出的稳定性修正系数计算公式是依据特定工况下安全系数值给出,为了论证修正系数计算公式是否可行,进行了如下工况的数值模拟.
3.1 计算工况
以下计算工况采用表1、表2中的物理力学参数以及图2中的计算模型.
工况1:当软弱土层厚度为10 m,且椭圆形软土层的长轴与路基和山体的交点A重合时,模拟当山体与坡脚之间的距离S=5 m时的稳定性安全系数.
工况2:当山体与坡脚之间的距离S=7 m,软弱土层为5 m,模拟当软弱土层的长轴为22 m时的稳定性安全系数.
3.2 计算结果分析
3.2.1 有限元模拟结果
通过有限元软件PLAXIS,采用表1和表3中的物理力学参数,分别对工况1和工况2进行数值模拟,得到相应工况的稳定性安全系数见表7.

表7 安全系数计算结果
3.2.2 修正系数计算
利用上一节中关于相应工况下的稳定性安全系数的计算公式,分别计算工况1和工况2的修正系数,见表8.

表8 安全系数修正
3.3 结果对比
根据表7中的安全系数计算结果可以发现:在不考虑地形因素的影响下,5 m的软弱土路基和10 m的软弱土路基稳定性安全系数相差很多,但是有限元模拟出的结果却相差不大.
将Janbu法的计算结果分别乘以计算得到的修正系数,得到相应工况的修正安全系数值,见表9.

表9 修正后的安全系数
计算结果与数值模拟结果相近,说明本文提出的修正系数计算公式具有一定的可行性.
4 结 论
1)山谷间软弱土路基稳定性,不仅与经典的边坡参数,还和路基坡脚到山谷坡脚之间的距离S,软弱土层长短轴长度a、b等特征性参数有关.
2)传统的Janbu法在计算谷间软弱土路基边坡稳定性系数时不考虑山体对其影响,需要进行修正.
3)通过有限元极限平衡法计算可知,随着山体与坡脚的距离S的增加,谷间软弱土路基边坡安全系数总体上先增加后减小,最后趋于平稳.
4)拟合有限元极限平衡法的结果,得到Janbu法计算谷间软弱土稳定性系数的修正曲线.试算结果说明该修正考虑了山体与软弱下卧层的影响,具有一定的合理性.
[1] 刘雪岭,苏生瑞,周新民.山区公路软基病害研究[J].地球科学与环境学报,2005,27(1):65-69.
[2] 郭进梅,赵世科.浅谈山区公路软基病害[J].中国水运月刊,2008,8(7):179-180.
[3] 刘望坤.山区高速公路软土路基变形特性研究[D].重庆:重庆交通大学,2013.
[4] 王瑞甫,王佳权,刘宏力,等.斜坡软土路基稳定性分析及治理方法研究[C].全国工程地质学术年会.2011.
[5] 杨 兵,陈谦应.塑料排水板在山区软基处治中的应用[J].西南公路,1991(4):22-27.
[6] 马 俊.CFG桩和砂桩处理山区高速公路软基[J].公路与汽运,2005(3):144-145.
[7] 冯永财.碎石桩与塑料排水板加固山区软弱路基比较研究[D].成都:成都理工大学,2013.
[8] 崔 溦.山区高速公路沟谷软基处理技术研究[D].天津:天津大学,2005.
[责任编辑 周文凯]
Study of Calculation Method of Subgrade Stability in Valley Soft Soil
Zhou Ying1,2Hong Baoning1,2Liu Xin1,2Gan Liangqin1,2Pu shikun1,2,3
(1. Key Laboratory of Ministry of Education for Geomechanics & Embankment Engineering, Hohai Univ., Nanjing 210098, China;2. Geotechnical Research Institute, Hohai Univ., Nanjing 210098, China; 3. PLA University of Science and Technology, Nanjing 210007, China)
The calculation of the stability of valley subgrade in mountain area is still using the method of traditional limit flatness without considering the effect of valleys on subgrade and the stability of valley soft soil. Based on the existence of the soft soil layer between the bottom of the pot and the effect of the adjacent mountain on the stability of the subgrade, the characterization parameters of the stability of the soft soil subgrade in the valley and the calculation formula of the correction coefficient are determined. The calculation formula of the correction coefficient of subgrade stability under different soft soils is obtained. By comparison of the working conditions, it is found that the calculated results are close to those calculated by using the stability correction coefficient proposed in this paper, so as to verify the feasibility of the stability correction coefficient calculation formula.
soft soil; stability characterization parameter; finite element; modification coefficient
2016-12-05
广东省交通运输厅科技项目《基于稳定性控制的山丘地区软弱路基优化处理方法研究》(科技-2015-02-015);国家自然科学基金青年基金(51609071);江苏省自然科学基金青年基金(BK20140848)
洪宝宁(1960-),男,教授,主要从岩土体基本特性研究.E-mail:hongbaoning24@sohu.com
10.13393/j.cnki.issn.1672-948X.2017.03.013
TU470+.3
A
1672-948X(2017)03-0058-04

