简谐激励作用下强非线性吸振器的能量转移效能
陈建恩,刘 军,葛为民,孙 敏
(1.天津理工大学 天津市先进机电系统设计与智能控制重点实验室,天津 300384;2.天津城建大学 理学院,天津 300384)
简谐激励作用下强非线性吸振器的能量转移效能
陈建恩1,刘 军1,葛为民1,孙 敏2
(1.天津理工大学 天津市先进机电系统设计与智能控制重点实验室,天津 300384;2.天津城建大学 理学院,天津 300384)
以单自由度主结构承受简谐激励作用时强非线性吸振器的减振能力作为研究对象,运用复变量平均法获得系统的慢变方程,并进一步得到描述稳态响应的非线性方程组。通过对比复变量平均法和龙格库塔获得的解,验证推导过程的正确性。利用复变量平均法分析吸振器的能量转移效能及其恒定性。研究结果显示,不同激励幅值下系统的频率响应存在较大差异。当激励幅值相对较小时,吸振器的减振效果明显。随着简谐激励幅值的增加,吸振器的能量转移效能无法保持恒定,系统在一定频带内出现高低两个稳定响应分支,并且两个响应分支会随着激励幅值的进一步增加而合并。
振动与波;强非线性吸振器;复变量平均法;能量转移;恒定性
靶向能量转移,或称为定向能量传递,是一种从主结构将能量单向不可逆地传递至非线性振子的能量转移方式,由此而衍生出的强非线性吸振器具有纯非线性刚度(弹簧回复力不具有线性部分)以保证能量传递的实现[1–2]。传统的调谐质量阻尼器除利用阻尼耗散振动能量外,还需依靠自身惯性力抵消主结构的振动,因此需要具有较大的质量。另外,调谐质量阻尼器需要与主结构的某一阶模态发生共振以对该模态实现减振,因此,其减振频带较窄。强非线性吸振器是通过非线性弹簧完成能量转移并利用阻尼对能量加以消耗,它具有两大显著优点,一是其质量可以远小于主结构,二是可以在宽频带内实现减振。一些学者对调谐质量阻尼器和强非线性吸振器的性能进行了对比[3–4],研究表明,除上述两个优点之外,在合理优化吸振器参数的前提下,强非线性吸振器具有较强的减振能力。
过去十余年时间内,对于强非线性吸振器的研究主要集中在两个方面,一方面是将吸振器应用于承受不同形式激励的各种结构或装置,另一方面是优化强非线性吸振器的结构以提高其能量转移效能(吸能百分比)。Kerschen等研究了强非线性吸振器对两自由度主结构的减振能力,研究表明吸振器可同时从主结构的两个自由度吸收能量[5]。Georgiades和Vakais将强非线性吸振器应用于简支梁和悬臂板并对吸振器参数进行了优化[6–7]。Ahmadabadi和Khadem研究了接地与不接地强非线性吸振器对于冲击载荷作用下的悬臂梁的减振效能[8]。Tumkur等利用强非线性吸振器抑制圆柱体的涡激振动[9]。Luo等研究了强非线性吸振器对六层建筑模型的减振效能[10]。Guo等将强非线性吸振器用于抑制转子在临界速度时的回转振动[11]。Izzi等利用强非线性吸振器抑制斜拉索的振动[12]。Lee等利用强非线性吸振器抑制两自由度机翼模型的气动失稳[13]。陈勇利用强非线性吸振器对高耸结构进行了振动抑制[14]。Zhang等研究了风载作用下轴向运动弦线在强非线性吸振器作用下的动态特性[15]。
Zhang等利用具有并联双振子的强非线性吸振器对轴向运动梁进行了振动抑制[16]。Tsakirtzis等研究了具有多自由度振子的强非线性吸振器的能量转移效能[17]。Lamarque等研究了具有非光滑部件的强非线性吸振器在冲击载荷和简谐载荷下的减振能力[18]。Gendelman和Starosvetsk等研究了简谐激励作用下含强非线性吸振器的系统的响应,并利用分段二次阻尼消除特定情况下的高响应分支[19–20]。Manevitch等研究了具有双稳态部件的强非线性吸振器的能量转移[21]。Shudeifat等研究了具有负刚度线性弹簧和非线性弹簧的吸振器的性能[22]。Benarous等分析了具有内嵌转子的强非线性吸振器的性能[23]。张也弛等分别研究了单、双自由度强非线性吸振器的减振性能[24–25]。Mattei等利用双稳态强非线性吸振器抑制双梁系统的振动[26]。熊怀等通过研究非保守系统和对应保守系统的能量耗散关系,提出了一种刚度设计方法[27]。
目前,对于冲击载荷作用下强非线性吸振器效能的研究较多,而对于其他形式激励作用下吸振器性能的研究偏少,并且,对于较大载荷作用下吸振器性能的研究更加缺乏。本文主要研究单自由度主结构承受简谐激励作用时强非线性吸振器的能量转移效能以及较大简谐载荷作用下能量转移效能的恒定性,总结了系统响应随着激励幅值增加而呈现出的演化规律。
1 动力学系统
单自由度主结构和单自由度强非线性吸振器所构成的系统如图1所示,其动力学方程可表述如下
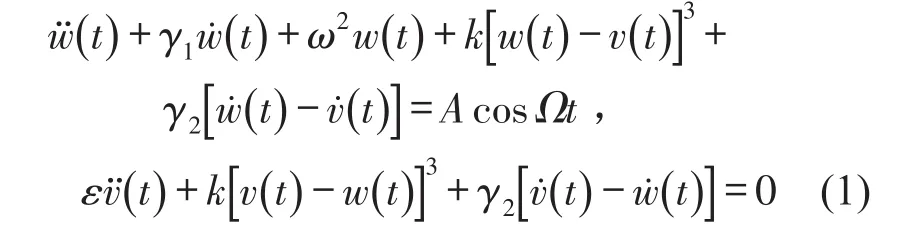
其中w和v分别表示主结构和非线性振子的位移,ω为主结构固有频率,ε为吸振器与主结构质量比,并满足0<ε<<1,A表示激励幅值,Ω表示激励频率,强非线性吸振器具有立方非线性刚度。方便起见,令Μ=1。

图1 连接强非线性吸振器的单自由度线性主结构
运用复变量平均法获得系统的慢变方程,首先引入如下变换

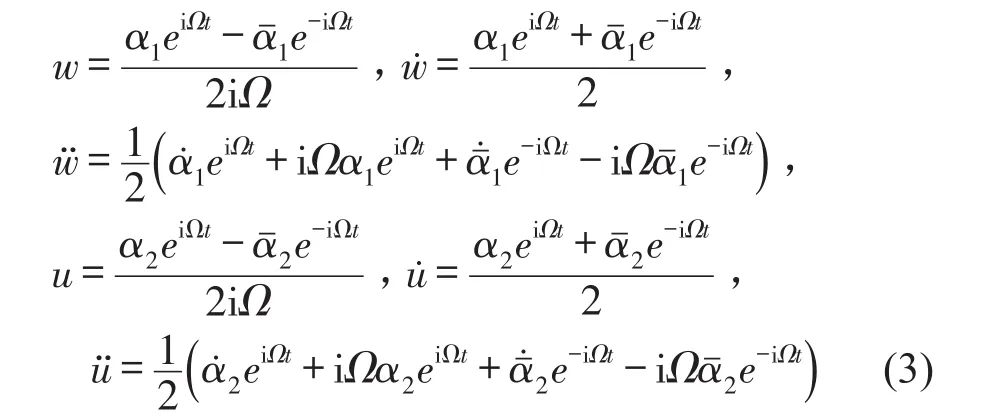
将式(3)代入方程(1),并保留慢变部分,可得

其中a1、b1、a2、b2均为t的函数。将上式代入方程(4),分离实部和虚部,可得



求解非线性代数方程组式(6),可以获得主结构的振幅以及主结构与非线性振子之间的相对运动幅值,其表达式分别为

为了判断系统稳态响应的稳定性,令

其中a10、b10、a20、b20是方程(5)的稳态解,δn(n=1、2、3、4)表示稳态解的小扰动,将式(8)代入方程组(5)并且仅保留关于扰动的线性部分,可得

方程(9)的系数矩阵如下,可运用其特征根判断稳态解的稳定性,当稳态解的所有特征根均具有负实部时,该解为稳定解。

2 数值验证
为了验证推导过程的正确性,将复变量平均法和龙格库塔获得的结果进行对比,如图2、图3所示。为了获得具有普适性的结果,仿真中的所有参数均采用无量纲量。通过调节主结构系数,可使ω=15。图2为激励幅值A=1时主结构与非线性振子间的相对运动,通常用该相对运动描述两振子间的能量转移效能[1],其中,图2(a)为相对运动的频率响应。通过系数矩阵(10)的特征值可以判断,Ω=15时系统运动是稳定的,而Ω=15.3时系统运动是不稳定的。图2(b)和图2(c)分别为Ω=15和Ω=15.3时的波形图,两图由龙格库塔法获得,波形图显示的结果与复变量平均法判断的结果相符,Ω=15.3时的波形图呈现出强调制响应。仿真过程中,系统的参数选取如下:γ1=0.1、ε=0.1、γ2=0.2、k=500。
图3给出了主结构的频率响应以及在两个不同激励频率下的波形图,同样,复变量平均法和龙格库塔获得的结果吻合较好。
图4为未连接和已连接强非线性吸振器的主结构的振动情况对比,结果显示,强非线性吸振器在该激励幅值下可以大量耗散主结构的振动能量,取得良好的减振效果。
3 能量转移效能及其恒定性
本节主要分析不同激励幅值下主结构与非线性振子间的能量转移效能以及转移效能的恒定性。图5为A=0.5时的系统响应,在整个响应频带内,稳态解都是稳定的,从图5(b)可以看出,强非线性吸振器对主结构产生良好的减振效果。

图2 A=1时主结构与非线性振子间的相对运动

图3 A=1时主结构的振动

图4 A=1时连接与不连接强非线性吸振器的主结构振动

图5 A=0.5时系统的响应
图6为A=2时的系统响应,当激励频带处于12.6~14范围内时,系统在每个激励频率下均存在三个解,其中包括两个稳定解,即系统存在高、低两个响应分支。当激励频带处于14.6~15.8范围内时,系统仅存在一个不稳定解,系统呈现出强调制响应。当激励频带处于15.9~16.4范围内时,系统存在三个解,其中仅有一个稳定解,主结构将始终处于较低的幅值。
图7为A=5时的系统响应,当激励频带处于8.3~12.9范围内时,系统存在两个稳定解,两个解对应的两个振子间相对运动相差较大,而对应的主结构的两个不同振动幅值在这一频带内相差较小。当激励频带处于15.2~16.7范围内时,系统仅存在一个不稳定解。在图中的其余频带内,系统仅存在一个稳定解,部分频带内有两个不稳定解与稳定解共存。
如图7(a)所示,高低两个响应分支发生了合并,可参照图6(a)观察,然而这种合并并未使减振效果有所改善。当激励频带处于12.9~14.2范围内时,主结构的振幅较大,强非线性吸振器的减振效果并不明显,吸振器主要使主结构的共振频率发生了变化,如图7(b)所示。
图8为A=8时的系统响应,当激励频带处于5.9~10.8范围内时,系统存在两个稳定解,然而这一频带并不在共振频带内,主结构的振幅一直较低。在图中的其余频带内,系统仅存在一个稳定解。在该激励幅值下,主结构的共振幅值较大,强非线性吸振器基本未显示减振效果。
通过上述分析可知,强非线性吸振器与主结构间的能量转移随着激励幅值的增加发生较大变化。激励幅值相对较小时,吸振器减振效果明显,随着激励的增大,在共振带内出现不稳定的强调制响应,强调制响应有利于能量的转移[1,2],即有利于减振,但是该响应的发生也标志着主结构的高响应分支即将出现。继续加大激励,高响应分支出现,其对应的频带内,强非线性吸振器减振效果明显降低。进一步加大激励,高响应分支将会与低响应分支在局部合并,高响应分支对应的频带变宽。继续增加激励幅值,高低两个响应分支几乎完全合并。

图6 A=2时系统的响应

图7 A=5时系统的响应

图8 A=8时系统的响应
通常以线性与非线性振子之间的相对运动衡量稳态能量转移效能[1],本文以整个频带内两振子之间的最大相对运动衡量强非线性吸振器的最大吸能能力。当激励幅值增大到一定值后,强非线性吸振器对主结构的减振效果明显降低乃至于失效。图9 (a)为最大相对运动随激励幅值的变化情况。当激励幅值从0.1增加至0.7的过程中,系统在整个激励频带内均仅存在一个稳定解,其频率响应与图5相似。两个振子的相对运动随激励幅值的增加而增加,然而,相对运动的增幅逐渐减小。激励幅值从0.8增加至1.2的过程中,系统出现不稳定解,其频率响应与图2相似。并且,随着激励幅值的增加,不稳定解所对应的频带逐渐变宽。激励幅值从1.3增加至4的过程中,系统在一定频带内存在两个稳定解,其频率响应与图6相似,在图9中,由高响应分支的最大相对运动反映吸振器的最大吸能能力,低响应分支的信息未在图中给出。随着激励幅值的继续增加,系统的频率响应分别与图7和图8类似。

图9 能量转移效能随激励幅值的变化情况
在激励幅值由1.3增加至8过程中,线性和非线性振子间的相对运动逐渐增加,然而,相对运动的增幅明显减小。结合图7(b)与图8(b)可知,随着输入能量的增加,吸振器无法始终以相同比例消耗能量,导致减振能力逐渐减弱。图9(b)为图9(a)的局部放大图。
本文仅给出了强非线性吸振器在一组参数下的仿真数据,任意改变吸振器参数,利用方程(6)和矩阵(10)即可获得相应结果,结果均与本文结果在定性上保持一致,鉴于篇幅限制,在此不再一一给出。
4 结语
利用复变量平均法研究了单自由度主结构承受不同幅值简谐激励作用时强非线性吸振器的能量转移效能。给出了能量转移方式和主结构响应随着激励幅值的增加而呈现出的演化规律。当激励幅值较小时,吸振器的吸振效果明显。然而,随着输入能量的增加,吸振器无法始终以相同比例消耗能量,导致减振能力逐渐减弱。其中,系统高响应分支的出现及其与低响应分支的合并是强非线性吸振器失效的主要原因。
本文研究了结构最为简单的强非线性吸振器,其缺点在大幅激励作用下较为明显,已有文献中未见有关于这一方面的系统性研究。可以从两个方面对这一缺点进行弥补,一是使用多个吸振器对主结构进行减振,在吸振器安装位置合理的前提下,这一方法可以成倍增强对主结构的吸振能力,然而在实际工程中,这种设置需要更多的安装空间并在一定程度上增加额外质量。二是改进强非线性吸振器结构,如引言所述,一些学者对强非线性吸振器结构进行了改进,然而,目前的改进主要关注吸振器在特定激励下的能量转移效能,关于消除高响应分支的方法非常缺乏。当主结构处于大幅不确定载荷作用下时,提高能量转移效能固然重要,加强能量转移效能的恒定性亦不可忽视。利用非线性控制理论探索消除高响应分支的方法,尤其是探索响应分支发生合并后,提高强非线性吸振器效能的方法,是应当进一步研究的重点。
[1]VAKAKIS A F,GENDELMAN O V,BERGMAN L A,et. Nonlinear targeted energy transfer in mechanical and structural systems[M].Berlin:Springer,2009.
[2]GENDELMAN V.Targeted energy transfer in systems with external and self-excitation[J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,2011,225(C9): 2007-2043.
[3]SAMANI F S,PELLICANO F.Vibration reduction on beamssubjected to moving loadsusing linearand nonlinear dynamic absorbers[J].Journal of Sound and Vibration,2009,325:742-754.
[4]PARSEH M,DARDEL M,GHASEMI M H,et al.Steady state dynamics of a non-linear beam coupled to a nonlinear energy sink[J].International Journal of Non-Linear Mechanics,2016,79:48-65.
[5]KERSCHEN G,KOWTKO J J,MCFARLAND D M,et al.Theoretical and experimental study of multimodal targeted energy transfer in a system of coupled oscillators [J].Nonlinear Dynamics,2007,47:285-309.
[6]GEORGIADES F,VAKAIS A F.Dynamics of a linear beam with an attached local nonlinear energy sink[J].Communications in Nonlinear Science and Numerical Simulation,2007,12:643-651.
[7]GEORGIADES F,VAKAKIS A F.Passive targeted energy transfers and strong modal interactions in the dynamics of a thin plate with strongly nonlinearattachments[J].International Journal of Solids and Structures,2009, 46:2330-2353.
[8]AHMADABADI Z N,KHADEM S E.Nonlinear vibration control of a cantilever beam by a nonlinear energy sink [J].Mechanism and Machine Theory,2012,50:134-149.
[9]TUMKUR R K R,DOMANY E,GENDELMAN O V,et al.Reduced-order model for laminar vortex-induced vibration of a rigid circular cylinder with an internal nonlinear absorber[J].Communications in Nonlinear Science and Numerical Simulation,2013,18:1916-1930.
[10]LUO J,WIERSCHEM N E,FAHNESTOCK L A,et al. Realization of a strongly nonlinear vibration-mitigation device using elastomeric bumpers[J].Journalof Engineering Mechanics,2014,140(5):04014009.
[11]GUO C Z,AL-SHUDEIFAT M A,VAKAKIS A F,et al. Vibration reduction in unbalanced hollow rotor systems with nonlinear energy sinks[J].Nonlinear Dynamics,2015,79:527-538.
[12]IZZI M,CARACOGLIA L,NOÈ S.Investigating the use of Targeted-Energy-Transfer devices for stay-cable vibration mitigation[J].Structural Control and Health Monitoring,2016,23:315-332.
[13]LEE Y S,VAKAKIS A F,BERGMAN L A,et al. Suppression of aeroelastic instability using broadband passive targeted energy transfers,part 1:theory[J].AIAA Journal,2007,45(3):693-711.
[14]陈勇,徐羿.基于非线性能量吸振器的高耸结构减振分析[J].振动与冲击,2014,33(9):27-32.
[15]ZHANG Y W,ZANG J,YANG T Z,et al.Vibration suppression of an axially moving string with transverse windloadingsbyanonlinearenergysink[J].Mathematical Problems in Engineering.2013,348042.
[16]ZHANG Y W,ZHANG Z,CHEN L Q,et al.Impulseinduced vibration suppression of an axially moving beam with parallelnonlinearenergy sinks[J].Nonlinear Dynamics,2015,82:61-71.
[17]TSAKIRTZIS S,PANAGOPOULOS P N,KERSCHEN G,et al.Complex dynamics and targeted energy transfer in linear oscillators coupled to multi-degree-of-freedom essentiallynonlinearattachments[J].NonlinearDynamics,2007,48:285-318.
[18]LAMARQUE C H,GENDELMAN O V,SAVADKOOHI A T,et al.Targeted energy transfer in mechanical systems by means of non-smooth nonlinear energy sink[J].Acta Mechanica,2011,221:175-200.
[19]GENDELMAN O V,STAROSVETSKY Y,FELDMAN M.Attractors of harmonically forced linear oscillator with attached nonlinear energy sink I:Description of response regimes[J].Nonlinear Dynamics,2008,51(1-2):31-46.
[20]STAROSVETSKY Y,GENDELMAN O V.Vibration absorption in systems with an onlinear energy sink: Nonlinear damping[J].Journal of Sound and Vibration,2009,324,916-939.
[21]MANEVITCH L I,SIGALOV G,ROMEO F,et al. Dynamics of a linear oscillator coupled to a bistable light attachment:Analytical Study[J].Journal of Applied Mechanics,2014,81(4):041011.
[22]AL-SHUDEIFAT M A.Highly efficient nonlinear energy sink[J].Nonlinear Dynamics.2014,76:1905-1920.
[23]BENAROUS N,GENDELMAN O V.Nonlinear energy sink with combined nonlinearities:Enhanced mitigation of vibrations and amplitude locking phenomenon[J].Journal of Mechanical Engineering Science,2016,230 (1):21-33.
[24]张也弛,孔宪仁,杨正贤,等.非线性吸振器的靶能量传递及参数设计[J].振动工程学报,2012,24(2):111-117.
[25]张也弛.基于非线性能量阱的双共振峰振动抑制的力学特性研究[J].航天器环境工程,2015,32(5):477-483.
[26]MATTEI P O,PONCOT R,PACHEBAT M,et al. Nonlineartargeted energy transferoftwo coupled cantilever beams coupled to a bistable light attachment [J].Journal of Sound and Vibration,2016,373:29-51.
[27]熊怀,孔宪仁,刘源.一类立方非线性吸振器的能量传递和耗散研究及参数设计[J].振动工程学报,2015,28(5):785-792.
Energy Transfer Efficiency of Nonlinear VibrationAbsorbers under Harmonic Excitations
CHEN Jian-en1,LIU Jun1,GE Wei-min1,SUN Min2
(1.Tianjin Key Laboratory of the Design and Intelligent Control of theAdvanced Mechatronical System, Tianjin University of Technology,Tianjin 300384,China; 2.School of Science,Tianjin Chengjian University,Tianjin 300384,China)
The efficiency of energy transfer from a single DOF primary structure subjected to harmonic excitation to a nonlinear vibration absorber is investigated.The slow flow equations of the system are derived by using complexificationaveraging method,and the nonlinear equations which describe the steady-state response are obtained.The resulting equations are verified by comparing the results which respectively obatined from complexification-averaging method and Runge-Kutta method.The energy transfer efficiency and constancy of the absorber are analyzed by using complexificationaveraging method.The results indicate that the frequency responses of the system are quite different under the excitation with different amplitudes.The vibration suppression effect of the absorber is excellent when the excitation amplitude is relatively small.With the increasing of the excitation amplitude,the energy transfer efficiency of the absorber cannot remain constant.The system will yield a lower stable branch and a higher stable branch,and the two branches will get closer and finally merge with the further increase of the excitation amplitude.
vibration and wave;strongly nonlinear vibration absorber;complexification-averaging method;energy transfer;constancy
O322;O328
:A
:10.3969/j.issn.1006-1355.2017.03.005
1006-1355(2017)03-0024-07
2016-12-19
国家自然科学基金资助项目(11402170,11402165)
陈建恩(1984-),男,山东省菏泽市人,讲师,主要研究方向为非线性动力学。Email:vchenje@163.com

