基于旋转变换的灰值形态算子

段 汕，樊金东

(1中南民族大学 数学与统计学学院，武汉 430074；2上海酷屏信息技术有限公司，上海200080)

基于旋转变换的灰值形态算子

段 汕1，樊金东2

(1中南民族大学 数学与统计学学院，武汉 430074；2上海酷屏信息技术有限公司，上海200080)

在二值旋转形态算子研究的基础上，研究了基于旋转变换的灰值形态算子的相关理论及方法，通过引入本影集合上的点积运算和灰值旋转变换等方法，将本影变换与表面算子应用于构建灰值旋转形态算子，提出并建立了基于空间旋转变换的灰值腐蚀、膨胀及开、闭算子，论证了一系列重要的性质，这些结论充实了基于旋转变换的形态学理论．

灰值旋转形态算子；本影变换；表面算子; 二值旋转形态算子

Serra的形态学理论[1]建立在空间平移变换的基础之上，平移形态算子通过平移变换实现对目标对象几何结构的探测过程．另一种常用的空间移动方式是旋转变换，在文献[2]中Heijmans提出了以旋转变换替代平移变换建立二值腐蚀、膨胀的思想．文献[3]对此进行了详细的研究，建立了二值旋转形态算子的相关理论．所有推证结果表明，在除去原点的空间中，二值旋转形态算子与二值平移形态算子具有相似的性质．本文在文献[3]的基础上，进一步研究了基于旋转变换的灰值形态算子的相关理论及方法，通过引入本影集合上的点积运算和灰值形态旋转变换等方法，将本影变换与表面算子应用于构建灰值旋转形态算子，提出并建立了基于空间旋转变换的灰值腐蚀、膨胀及开、闭算子，论证了一系列重要的性质，充实了基于旋转变换的形态学理论．研究结果表明：旋转形态算子与平移形态算子具有诸多类似的结构和性质[4-8]，这一结果与Heijmans的T不变算子理论是一致的．

1 预备知识

设En=Rn{0}表示连续n维欧式空间剔除原点的集合．灰值图像y=f(x)，x∈En其像素点x用极坐标(r,θ)描述，f定义域D[f]⊂En，(x,f)∈En+1，灰值图像f的全体构成的集合记为F．灰值图像集合F中的序关系可按以下方式给出[2]：如果g和f的定义域满足条件D[g]⊆D[f]，且对于任意的∀x∈D[g]有g(x)≤f(x)(默认超出定义域范围的值为负无穷)，则称g位于f的下方，或称g小于f，记为g≪f，由此可建立灰值图像的偏序集合(F,≪)．

在偏序集合(F,≪)中，可定义其上的极大和极小运算[2]：

(f∧g)(x)=min{f(x),g(x)},

x∈D[f]∩D[g],

(f∨g)(x)=max{f(x),g(x)},

x∈D[f]∪D[g],

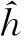
2 旋转变换下阴影集和表面函数的性质

灰值图像函数f的本影U[f]={(x,y):x∈D[f],y≤f(x)}[2,9],若D[f]⊂En，则U[f]⊆En+1．集合A的表面S[A]={(x,y)∈A：y≥z,∀(x,z)∈A}[2]，其表面函数具有形式S[A](x)=max{y|(x,y)∈A}．显然，对于任意的灰值图像函数f，其本影变换及表面函数具有如下关系[3]：

S(U[f])(x)=f(x).

(1)

且容易证明下面的结论成立：

(1)给定两个集合A和B，若A⊂B，则S[A](x)≤S[B](x)；

(2)对任意g和f，g≪f的充要条件是U[g]⊂U[f]．

对于∀(x,y),(h,k)∈U[f]，将向量的点运算 “·” 及逆元[3]概念扩展到U[f]中：

(x,y)·(h,k)=(x·h,y+k),

(2)

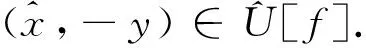
同时，引入灰值图像函数f的旋转变换fh,k：

(3)

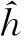
性质1 (1)U[fh,k]=(U[f])·(h,k)；

(2)Sh,k(U[f])(x)=fh,k(x).

证明 (1)

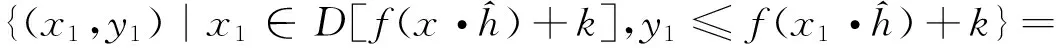
{(x·h,y+k)|x∈D[f],y≤f(x)}=

{(x,y)·(h,k)|(x,y)∈U[f]}=(U[f])·(h,k).

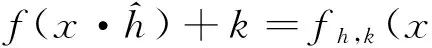
利用二值旋转形态算子的性质[3]，可建立本影变换、表面算子与极大极小运算及集合的交并运算之间的关系．

性质2 (1)U[f∧g]=U[f]∩U[g] ；

(2)S(U[f]∩U[g])=f∧g；

(3)U[f∨g]=U[f]∪U[g] ；

(4)S(U[f]∪U[g])=f∨g.

证明 (1)U[f∧g]={(x,y)|x∈D[f∧g],y≤(f∧g)(x)}={(x,y)|x∈D[f]∩D[g],y≤min{f(x),g(x)}}=

{(x,y)|x∈D[f],y≤f(x);x∈D[g],y≤g(x)}=

U[f]∩U[g] ;

(2)S(U[f]∩U[g])=S(U[f∧g])=f∧g;

(3)U[f∨g]={(x,y)|x∈D[f]orx∈D[g],y≤max{f(x),g(x)}}=

{(x,y)|x∈D[f],y≤f(x) orx∈D[g],y≤g(x)}=U[f]∪U[g] ;

(4)S[U[f]∪U[g]]=S[U[f∨g]]=f∨g.

3 灰值旋转形态算子的结构性质

利用本影变换和表面算子，在二值旋转形态算子[3]的基础上引入结构元素g对于目标图像f的灰值旋转形态腐蚀、膨胀及开、闭算子：

(4)

(5)

这里Θr,⊕r,∘r,·r表示二值及灰值旋转形态算子，以区别于平移形态算子．利用性质1和性质2，可以推出灰值旋转形态算子与灰值平移形态算子类似的表示及性质．下面首先研究灰值旋转形态算子的结构特征，以下性质给出了灰值旋转算子的数学表达式．

性质3 (1) (fΘrg)(x)=min{f(z·x)-g(z)|

z∈D[g],z·x∈D[f]};

证明 利用二值旋转形态腐蚀和膨胀的表达式[3]，有：

(1) (fΘrg)(x)=S[U[f]ΘrU[g]](x)=

max{y|(x,y)∈U[f]ΘrU[g]}=

max{y|U[g]·(x,y)⊆U[f]}=

max{y|(z,w)·(x,y)∈U[f],∀z∈D[g],w≤g(z)}=

max{y|(z·x,w+y)∈U[f],z∈D[g],w≤g(z)}=max{y|w+y≤f(z·x),z∈D[g],w≤g(z),z·x∈D[f]}=

max{y|y≤f(z·x)-g(z),z∈D[g],z·x∈D[f]}=

min{f(z·x)-g(z)|z∈D[g],z·x∈D[f]};

(2) (f⊕rg)(x)=S[U[f]⊕rU[g]](x)=

max{y|(x,y)∈U[f]⊕rU[g]}=

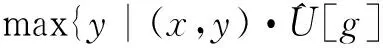
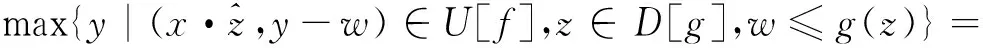
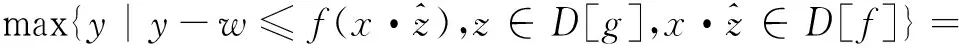
(3) (f∘rg)(x)=((fΘrg)⊕rg)(x)=

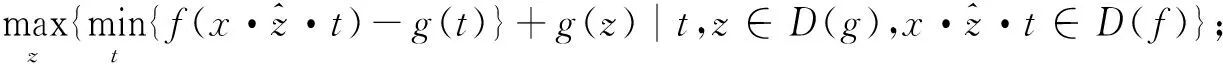
(4) (f·rg)(x)=((f⊕rg)Θrg)(x)=

性质4 (1)U[fΘrg]=U[f]ΘrU[g];

(2)U[f⊕rg]=U[f]⊕rU[g].

证明 利用二值旋转形态腐蚀和膨胀的表示式[3]和性质3，有：

(1)U[fΘrg]={(x,y)|x∈D[fΘrg],y≤(fΘrg)(x)}=

{(x,y)|x∈D[f]∩D[g],y≤f(z·x)-g(z),∀z∈D[g],z·x∈D[f]}=

{(x,y)|x∈D[f]∩D[g],y+g(z)≤f(z·x),z∈D[g],z·x∈D[f]}=

{(x,y)|y+w≤f(z·x),z·x∈D[f],w≤g(z),z∈D[g]}=

{(x,y)|(z·x,y+w)∈U[f],(z,w)∈U[g]}=

{(x,y)|(x,y)·(z,w)∈U[f],(z,w)∈U[g]}=

U[f]ΘrU[g];

(2)U[f]⊕rU[g]={(x,y)·(z,w)|(x,y)∈U[f],(z,w)∈U[g]}=

{(x·z,y+w)|x∈D[f],y≤f(x);z∈D[g],w≤g(z)}=

{(t,s)|t=x·z∈D[f]⊕rD[g],s=y+w≤f(x)+g(z)}=

{(t,s)|t∈D[f⊕rg],s≤(f⊕rg)(t)}=U[f⊕rg].

性质5 (1)f∘rg=(fΘrg)⊕rg；

(2)f·rg=(f⊕rg)Θrg.

证明 (1)由二值旋转开运算的性质[3]及(5)式，有：

f∘rg=S(U[f]∘rU[g])=

S((U[f]ΘrU[g])⊕rU[g])=

S(U[fΘrg]⊕rU[g])=

S(U[fΘrg⊕rg])=fΘrg⊕rg,

同理可证(2)．

该性质表明，灰值旋转形态开、闭算子是灰值旋转形态腐蚀和膨胀算子的复合形式．

性质6

(1)U[f∘rg]=U[f]∘rU[g];

(2)U[f·rg]=U[f]·rU[g].

证明 利用性质4和性质5，得：

U[f∘rg]=U[(fΘrg)⊕rg]=U[fΘrg]⊕rU[g]=

(U[f]ΘrU[g])⊕rU[g]=U[f]∘rU[g],

同理可证(2)．

下面的性质表明灰值旋转形态腐蚀、膨胀、开、闭算子满足对偶性．

性质7

证明 (1) (fΘrg)(x)=

min{f(z·x)-g(z)|z∈D[g],z·x∈D[f]}=

-max{-f(z·x)+g(z)|∀z∈D[g],z·x∈D[f]}=

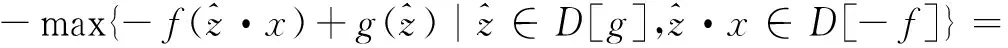
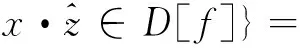
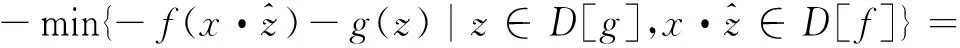
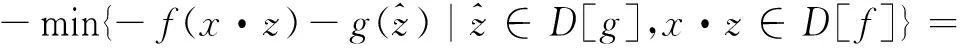
(3)f∘rg=(fΘrg)⊕rg=

(4)f·rg=(f⊕rg)Θrg=

性质8

(1)f⊕rg=g⊕rf；

(2)f⊕r(g⊕rh)=(f⊕rg)⊕rh；

(3)fΘr(g⊕rh)=(fΘrg)Θrh.

4 灰值旋转形态算子的代数性质

在研究了结构特征之后，进一步研究灰值旋转形态算子与其它相关运算之间的代数关系，首先，可以证明灰值旋转形态算子与极大、极小运算满足可交换性．

性质9

(1) (f∧g)Θrh=(fΘrh)∧(gΘrh)；

(2)fΘr(g∨h)=(fΘrg)∧(fΘrh)；

(3)f⊕r(g∨h)=(f⊕rg)∨(f⊕rh).

同时，灰值旋转形态算子对于目标对象满足旋转不变性，即灰值旋转形态算子具有旋转不变性，是一类旋转不变算子．

性质10

(1)fh,kΘrg=(fΘrg)h,k;

(2)fh,k⊕rg=(f⊕rg)h,k;

(3)fh,k∘rg=(f∘rg)h,k;

(4)fh,k·rg=(f·rg)h,k.

证明

(1)fh,kΘrg=S[U[fh,k]ΘrU[g]]=

S[((U[f])·(h,k))ΘrU[g]]=

S[(U[f]ΘrU[g])·(h,k)]=

S[(U[fΘrg])·(h,k)]=(fΘrg)h,k；

(2)fh,k⊕rg=S[U[fh,k]⊕rU[g]]=

S[((U[f])·(h,k))⊕rU[g]]=

S[(U[f]⊕rU[g])·(h,k)]=

S[(U[f⊕rg])·(h,k)]=(f⊕rg)h,k;

(3)fh,k∘rg=(fh,kΘrg)⊕rg=

(fΘrg)h,k⊕rg=((fΘrg)⊕rg)h,k=

(f∘rg)h,k;

(4)fh,k·rg=(fh,k⊕rg)Θrg=(f⊕rg)h,kΘrg=

((f⊕rg)Θrg)h,k=(f·rg)h,k.

灰值旋转形态膨胀对于结构元素同样满足旋转不变性.结构元素的位置对灰值旋转形态腐蚀和膨胀的结果有影响，但不会对灰值旋转形态开、闭运算的结果产生影响．

性质11

(2)f⊕rgh,k=(f⊕rg)h,k;

(3)f∘rgh,k=f∘rg;

(4)f·rgh,k=f·rg.

证明 (1)fΘrgh,k=S[U[f]ΘrU[gh,k]]=

S[U[f]Θr(U[g]·(h,k))]=

(2)f⊕rgh,k=S[U[f]⊕rU[gh,k]]=

S[U[f]⊕r(U[g]·(h,k))]=

S[(U[f]⊕rU[g])·(h,k)]=

S[(U[f⊕rg])·(h,k)]=(f⊕rg)h,k;

(3)f∘rgh,k=(fΘrgh,k)⊕rgh,k=

((fΘrgh,k)⊕rg)h,k=

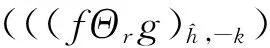
(4)f·rgh,k=(f⊕rgh,k)Θrgh,k=

灰值旋转形态算子还具有相关的保序性：

性质12 如果f≪g,则有：

(1)fΘrh≪gΘrh;

(2)f⊕rh≪g⊕rh;

(3)f∘rh≪g∘rh;

(4)f·rh≪g·rh.

证明 由f≪g⟺U[f]⊂U[g]，及二值旋转形态腐蚀、膨胀的递增性，得：

U[f]ΘrU[h]⊂U[g]ΘrU[h],

U[f]⊕rU[h]⊂U[g]⊕rU[h],即

U[fΘrh]⊂U[gΘrh],

U[f⊕rh]⊂U[g⊕rh],故

fΘrh≪gΘrh,f⊕rh≪g⊕rh;

进而有(fΘrh)⊕rh≪(gΘrh)⊕rh，(f⊕rh)Θrh≪(g⊕rh)Θrh，即：

f∘rh≪g∘rh，f·rh≪g·rh.

性质13 如果g≪h,则有fΘrh≪fΘrg,f⊕rg≪f⊕rh.

证明 由g≪h⟺U[g]⊂U[h]，利用二值旋转形态腐蚀、膨胀的相关性质得：

U[f]ΘrU[h]⊂U[f]ΘrU[g],

U[f]⊕rU[g]⊂U[f]⊕rU[h],

即U[fΘrh]⊂U[fΘrg]，U[f⊕rg]⊂U[f⊕rh]，

故有：

fΘrh≪fΘrg,f⊕rg≪f⊕rh.

性质14 如果U[g]包含单位原点，则fΘrg≪f≪f⊕rg.

证明 当(1,0)∈U[g]时，由二值旋转形态膨胀的扩展性和腐蚀的非扩展性及性质4知：

U[f]⊂U[f]⊕rU[g]=U[f⊕rg],

U[fΘrg]=U[f]ΘrU[g]⊂U[f],

故有f≪f⊕rg;fΘrg≪f.

由二值旋转形态开、闭运算的非扩展性、扩展性和幂等性，可证明灰值旋转形态开、闭运算具有类似的性质：

性质15f∘rg≪f≪f·rg.

性质16 (f∘rg)∘rg=f∘rg,(f·rg)·rg=f·rg.

5 结语

本文在文献[3]的基础上，通过将点积运算扩展到本影集合，提出了本影集合中的点积和逆元方法，以此将平面旋转变换引入到函数中，建立了灰值图像函数的旋转变换，为利用本影变换和表面算子构造旋转形态算子提供了必备条件．函数的旋转变换与本影和表面算子之间关系的建立为研究旋转形态算子提供了基础．

本文研究了灰值旋转形态腐蚀、膨胀、开、闭算子结构的建立及相关性质、方法，得出了有关算子表示、结构特征、代数性质等一系列重要结论，使得基于旋转变换的旋转形态学的理论和方法更加完善．

[1] Serra J. Image analysis and mathematical morphology[M].New York: Academic Press,1982：217-296.

[2] Heijmans H. Morphological image operator[M]. Boston: Academic Press,1994：17-96.

[3] 段 汕，樊金东，赖国琴，等. 基于旋转变换的二值形态算子的研究[J]. 中南民族大学学报(自然科学版)，2015,34(2):122-126.

[4] Stemberg S R. Gray-scale morphology[J]. Computer Vision, Graphics and Image Processing, 1986(2):333-355.

[5] Ronse C .Why mathematical morphology needs complete lattices[J]. Signal Processing, 1990,21(2): 129-154.

[6] Maragos P, Ziff R.Threshold superposition in morphological image analysis systems[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990,12(5): 498-504.

[7] Heijmans H, Ronse C. The algebraic basis of mathematical morphology: dilations and erosions[J]. Computer Vision, Graphics and Image Proccssing: Image Understanding, 1990,50(6): 245-295.

[8] Heijmans H. Theoretical aspects of gray-level morphology[J]. IEEE Transactions on Patten Analysis and Machine Intelligence, 1991,13(6): 568-582.

[9] Heijmans H. A note on the umbra transform in gray-scale morphology[J].Pattern Recognition Letters, 1993,14(11): 811-877.

Gray-Value Morphological Operators Based on Rotation Transform

DuanShan1,FanJindong2

(1 College of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074, China;2 Shanghai Kuping Information Technology Systems Co., Ltd, Shanghai 200080,China )

Based on the binary rotation morphological operators, the research on related theory and method of the gray-value morphological operator with rotation transform was proposed. By introducing the dot product operation of the umbra set and gray-value rotation transform for gray-value images, umbra transform and surface operator were applied to build gray-value rotation morphological transform, including erosion, dilation, opening and closing operator. The main structures and properties were considered, and the methods for solving them within the framework of rotation morphological operator were described,some important properties were obtained and they enriched the rotation morphology.

gray-value rotation morphological transform; umbra transform; surface operator; binary rotation morphological transform

2017-02-22

段 汕(1962-)，女，教授，博士，研究方向：数学应用方法与图像处理，E-mail:duanshan@mail.scuec.edu.cn

国家自然科学基金资助项目(61374085)

TP391.41

A

1672-4321(2017)02-0138-05