基于BKW状态方程的爆轰产物及参数的改进算法
何伟平,黄 菊,陈厚和,刘晓静,王德堂,4
(1.徐州工业职业技术学院化学工程学院,江苏 徐州 221140; 2.徐州工程学院化学化工学院,江苏 徐州 221111; 3.南京理工大学化工学院,江苏 南京 210094; 4.徐州工业职业技术学院江苏省化工新材料工程技术研发开发中心,江苏 徐州 221140)
基于BKW状态方程的爆轰产物及参数的改进算法
何伟平1,黄 菊2,陈厚和3,刘晓静1,王德堂1,4
(1.徐州工业职业技术学院化学工程学院,江苏 徐州 221140; 2.徐州工程学院化学化工学院,江苏 徐州 221111; 3.南京理工大学化工学院,江苏 南京 210094; 4.徐州工业职业技术学院江苏省化工新材料工程技术研发开发中心,江苏 徐州 221140)
为了降低爆轰产物及爆轰参数的求解难度,通过对质量守恒方程的基本可行解进行线性组合,得到了爆轰产物的平衡组成,并在此基础上进一步获得了爆轰参数。其主要实现方法为:由最小自由能原理对基本可行解进行筛选,然后根据最大放热原则确定初始解,并在最小自由能原则的引导下,由初始解和基本可行解的线性组合获得爆轰产物的平衡组成,以上操作步骤均由自编程序完成。应用支持向量机(SVM)线性模型对BKW状态方程参数进行了调整,并详细介绍了其主要步骤。使用此方法预测了PETN、CL-20和含铝炸药的爆轰产物及爆轰参数,经参数调整后,发现预测结果与实验值吻合良好;通过与单质炸药爆轰实验数据对比,发现调整BKW状态方程参数时,应当尽可能使用爆轰产物中气体含量相近的含能材料对SVM模型进行训练;若预测含铝炸药,应当使用铝氧比接近待测炸药的样品来训练SVM模型。
爆炸力学;BKW状态方程;基本可行解;支持向量机;SVM;吉布斯自由能
引 言
含能材料爆轰参数及产物的计算离不开爆轰产物的状态方程[1]。从20世纪40年代起,各国研究者对爆轰产物状态方程作了大量研究,提出了各种数学物理模型,如美国的BKW、JCZ、JWL等[2-4],日本的KHT[5],前苏联的BKWRR,以及我国的VLW等[6-8],并根据状态方程发展了各种计算程序[3,9-11]。其中,BKW状态方程作为典型的爆轰产物状态方程,在国际上取得了广泛的应用和发展[12-14]。
由于BKW状态方程对维里方程取一级近似,对工业炸药和高能炸药往往不能准确预测[1,15],研究者通常采取调整系数的方法来进行改进[16-18],但关于系数的调整方法却鲜见报道。另一方面,通常采用最小自由能法来求解爆轰产物及参数问题,并引入拉格朗日因子将条件极值转化为非条件极值,通过反复迭代进行计算,过程复杂而且会带来误差[13,18],甚至会因为收敛困难而导致求解失败。由于传统的求解方式借助牛顿迭代法完成,其收敛速度与目标函数的偏导函数有关,故具有一定的不确定性,并且涉及到偏导函数的计算,其过程十分复杂。本文在前期研究[19]的基础上,利用爆轰产物的基本可行解,通过简单的线性组合来获取爆轰产物的平衡组分,该计算方法原理可靠、过程简洁,得到的爆轰产物组成严格遵守质量守恒原则;在此基础上计算爆轰参数,可降低计算的复杂程度和避免迭代带来的误差;此外,采用支持向量机理论(SVM)[20],结合自编程序调整了BKW状态方程参数。
1 爆轰产物和参数的计算方法
1.1 问题描述
采用最小自由能法求解爆轰产物,其数学模型可简述如下:
(1)
式中:下标g、s分别表示气态产物和凝聚态产物;G为吉布斯自由能;x为产物的物质的量;μ为化学势;aik、ajk分别为每摩尔第i、j种产物中含有第k种原子的物质的量;bk为体系第k种原子的总物质的量;E为爆轰产物比内能;E0为炸药比内能;P、ν分别为爆轰状态的压强、产物比体积;P0、ν0分别为初始的压强、炸药比体积。其中,μgi、μsj、E均为关于温度(T)、压强(P)、产物组成(xg1,…,xgm,xs1,…,xgn)的函数,其具体表达形式见文献[16]。
1.2 基本可行解的处理
计算爆轰参数的关键是确定爆轰产物的平衡组成。在以往研究中,通常采用拉格朗日乘数法将式(1)的质量守恒方程与吉布斯自由能组合为新的目标函数,通过牛顿迭代法,将Hugniot关系作为终止判据进行求解,但其计算过程极为繁琐[18]。本研究直接求解质量守恒方程,利用线性组合搜索最优解,降低了计算的复杂程度;并通过优化搜索方法,保证了计算效率和精度。
该算法的基本原理为:爆轰产物的任意一种可能组成Xi=(xgli,…,xgmi,xsli,…,xgni),均可视为式(1)中质量守恒方程的(m+n-l+1)个基本可行解{X1,X2,…,Xm+n-l+1}的线性组合。本研究基本可行解是指:从(m+n)种产物中选取l种,代入求解质量守恒方程,若解存在,则该解称为基本可行解。
通常在假定温度和压强下求解平衡组分,此时吉布斯自由能为X=(xg1,…,xgm,xsl,…,xgn)的连续函数;另一方面,爆轰产物的平衡组分(Xopt)处于吉布斯自由能的最低点,故在其他条件未知的情况下,选取吉布斯自由能最小的(m+n-l+1)个基本可行解进行线性组合较为合理。
1.3 组分迭代
初始解(X0)的选取也很重要,若将X0设定在Xopt附近,则有利于求解。同时考虑程序编写的简便性,本研究采用“最大放热原则”确定X0,计算结果表明可以很好地收敛到Xopt。
将筛选出的(m+n-l+1)个基本可行解按其吉布斯自由能升序排列,依次与X0线性组合:Xt1=(1-r)X0+rXi(0 若一轮比较结束后,X0仍未发生变化,则令r′=0.5r(r初始值设为0.1),将r′作为新的r,进入下一轮比较和替换,直至r达到设定的精度则停止搜索,即认为得到该温度和压强下的最优解Xopt=X0。 1.4 温度和压强迭代 获得某温度和压强下的最优解Xopt后,计算f(P,T)=(E-E0)-0.5(P+P0)(ν0-ν)。若f(P,T)>0,则降低温度;若f(P,T)<0,则升高温度。重新进行平衡组分的计算,直至f(P,T)达到预定的精度,该操作可采用二分法完成。 爆轰产物的比体积(ν)可以由BKW状态方程和凝聚态产物的状态方程(如Cowan方程)计算得到。爆轰产物平衡组分、爆轰温度分别由前述方式确定的条件下,改变P,即可得到相应的ν。由于Hugoniot曲线上C-J点的爆速最小,利用最小抛物线法反复迭代,即可确定爆轰C-J点[18]。 2.1 获取训练数据 根据平衡组分的搜索方法,利用Visual Basic 6.0编制爆轰参数计算代码,涉及产物的热力学数据来自美国国家标准与技术局(NIST)数据库。保持α=0.5,选取β=0.140~0.180,θ=300~500,κ=10~12,根据{β,θ,κ}的不同组合,计算若干个炸药的爆压(P)和爆速(D)并与实验值比较,将结果记为“偏低”和“偏高”两类。 2.2 构造SVM模型 支持向量机(SVM)线性规划模型[21]可表示为式(2),其对应最优超平面为A(ω+-ω-)-γ=0。 (2) (3) 构造向量C、W(待求向量)、b、LB及系数矩阵A(上标M、H表示所属分类): (4) (5) 2.3 训练结果 根据构造的SVM模型,利用Matlab求解并绘制最佳分割平面,其结果如图1所示。 由图1(a)~(f)可见,利用SVM线性模型可以完整地划分两类结果(“偏低”、“偏高”),故其最佳分割平面即为BKW状态方程参数的合理取值范围。由图1(g)~(h)可知,各最佳分割平面沿β、κ方 向升降较为明显,而沿θ方向较为平坦;故在调整参数时,θ的调整幅度不宜过小。另外,对比图1(g)~(h)可见各最佳分割平面的相互关系并无一致规律,其具体参数见表1。 表1 最佳分割平面的相关参数Table 1 Relevant parameters of the optimal classifying planes 2.4 数据处理 为了使调整后的参数{β,θ,κ}尽可能满足同类含能材料爆轰参数的计算,选取点(β,θ,κ)使其与表1中6个最佳分割平面的距离di总和为最小,即: (6) 保持α不变,可得β=0.184,θ=1080,κ=10.76,以此作为BKW状态方程参数进行爆轰产物及参数的计算。 3.1 PETN和CL-20炸药爆轰参数的验证及优化 为了验证本算法的准确性,采用标准生成焓为-502.8kJ/mol、密度为1.77g/cm3的PETN[22],以及标准生成焓为460.0kJ/mol、密度为2.04g/cm3的CL-20[22-24]进行验证,计算得到爆轰参数见表2。 由表2可见,PETN的预测爆压准确性虽高于BKW方法,但低于文献方法;预测爆速的准确性虽高于文献方法,但低于BKW方法。分析其原因,可能是BKW状态方程本身存在缺陷[1],使得调整的参数不具备普适性。故需要根据类似炸药或自身实验进一步调整BKW状态方程参数。 表2 PETN和CL-20炸药爆轰CJ点的爆轰参数Table 2 Detonation parameters of PETN and CL-20 at C-J point 参照爆轰产物中气体所占的质量分数以选取BKW参数的方法,单位质量PETN、RDX、HMX、CL-20、TATB生成的气体产物质量分别为1.206、1.172、1.172、1.077、0.971。CL-20的产气质量位于RDX、HMX与TATB之间,故BKW参数不再进行调整,CL-20的预测值与文献数据相比,爆压、爆速的误差分别为4.65%、1.14%;但PETN与TATB差异较大,与RDX、HMX则较为接近,故选取点(β,θ,κ)使其与RDX、HMX涉及的4个最佳分割平面的距离总和最短,可得β=0.176、θ=540、κ=10.81。重新计算PETN爆轰参数得P=34.0GPa,D=8388m/s,T=2963K,PETN爆轰产物物质的量见表3。经过参数调整后,本方法计算爆压、爆速的误差分别为1.49%、1.06%,可见与实验值吻合良好。 表3 1 摩尔 PETN炸药C-J点的爆轰产物物质的量Table 3 The amount of detonation product for 1 mol PETN at C-J point 实际上,若利用PETN的实验值对不同BKW状态方程参数组合下的爆压、爆速和爆温进行检验,可得SVM最佳分割平面如图2所示,BKW状态方程参数的较好取值为(β,θ,κ)=(0.149,1425,12.26)。经自编程序验证,在该BKW状态方程参数取值下,PETN的爆压、爆速和爆温预测值分别为P=34.0GPa、D=8326m/s、T=3432K,误差分别为1.49%、0.31%、0.94%。 利用CL-20的文献数据对不同BKW状态方程参数组合下的爆压和爆速进行检验,可得SVM最佳分割平面如图3所示,BKW状态方程参数的较 好取值为(β,θ,κ)=(0.148,15,10.76)。在该BKW状态方程参数取值下,CL-20的爆压、爆速预测值分别为P=44.0GPa、D=9600m/s,误差分别为2.3%、0。 3.2 含铝炸药爆轰参数的验证 与前述理想炸药不同,由于含铝炸药中的铝颗粒在爆轰过程中的化学反应滞后于C-J爆轰反应,因此一般认为铝粉在爆轰过程中是惰性的,故求解过程中铝粉按惰性物质处理。为了方便与实验数据对比,选取文献[25]编号为2~6的RDX基含铝炸药为研究对象,其配方及爆轰参数测定结果[25]如表4所示。 表4 RDX基含铝炸药配方及爆轰参数测定结果Table 4 The formulation and the testing results of detonation parameters of RDX-based aluminized explosives 保持α=0.5,β=0.160,选取θ=2500~3500,κ=10.00~12.00,根据{θ,κ}的不同组合,计算4号含铝炸药的爆压和爆速,并与实验值进行对比分类,结果见图4。 在观测范围内,(θ,κ) 的一个较好取值为(3100, 10.75)。以此作为BKW状态方程参数,计算得到2~6号含铝炸药的爆轰参数见表5。 表5 RDX基含铝炸药爆轰参数的计算结果Table 5 The calculation results of detonation parameters for RDX-based aluminized explosive 计算结果表明,当铝氧比接近4号含铝炸药时,爆压的预测值与实测值较为接近,反之预测值误差较大;因此,使用调整BKW参数的方法预测含铝炸药的爆压时,应当在待测炸药的铝氧比接近训练样本的情况下使用。爆速的预测值则较为准确,最大误差为5.90%,而且预测值与实测值变化趋势基本一致。 (1)介绍了利用SVM模型优化BKW状态方程参数的方法。直接求解质量守恒方程,利用其基本可行解进行线性组合,并充分结合最小自由能原理,可以方便地求解爆轰产物的平衡组分。 (2)根据自编程序验证,使用SVM线性模型可以有效地获得BKW状态方程参数的合理取值。 (3)通过对比发现,利用BKW状态方程预测含能材料的爆轰参数时,应当使用爆轰产物中气体所占质量分数相近的含能材料的爆轰参数训练SVM模型(若预测含铝炸药,则应当使用铝氧比接近待测炸药的样品训练SVM模型),获取的优化参数才具有适用性。 [1] 吴雄,龙新平,何碧,等.VLW状态方程的回顾与展望[J].高压物理学报,1999,13(1):55-58. WU Xiong, LONG Xin-ping, HE Bi, et al.Preview and look forward to the progress of VLW equation of state[J]. Chinese Journal of High Pressure Physics, 1999, 13(1): 55-58. [2] Mader C L.Recent advances in numerical modeling of detonations[J].Propellants, Explosives, Pyrotechnics, 1986, 11(6): 163-166. [3] Mader C L.Numerical modeling of explosives and propellants[M].3rd Edition.Boca Raton:CRC Press Inc, 2008: 31-63. [4] 宋浦, 杨凯, 梁安定,等. 国内外TNT炸药的JWL状态方程及其能量释放差异分析[J]. 火炸药学报, 2013, 36(2):42-45. SONG Pu, YANG Kai, LIANG An-ding, et al.Difference analysis on JWL-EOS and energy release of different TNT charge [J].Chinese Journal of Explosives & Propellants(Huozhayao Xuebao), 2013, 36(2):42-45. [5] Katsum, Tanaka.Detonation properties of high explosives calculated by revised Kihara-Hikita equation of state[C]∥The Eighth Symposium(International) on Detonation. Annapolis:Naval Surface Weapons Center,1985: 548-557. [6] 高大元, 吕春绪, 董海山,等. 工业炸药的爆轰性能研究[J]. 火炸药学报, 2003, 26(1):26-29. GAO Da-yuan, Lü Chun-xu, DONG Hai-shan, et al.Study on detonation performance of industrial explosives [J].Chinese Journal of Explosives & Propellants(Huozhayao Xuebao),2003, 26(1):26-29. [7] 龙新平,何碧,蒋小华,等.论VLW状态方程[J].高压物理学报,2003,17(4):247-254. LONG Xin-ping, HE Bi, JIANG Xiao-hua, et al.Discussions on the VLW equation of state[J].Chinese Journal of High Pressure Physics, 2003, 17(4): 247-254. [8] Wu Xiong, Long Xin-Ping, He Bi, et al.VLW equation of state of detonation products[J].Science in China Series B:Chemistry, 2009, 52(5): 605-608. [9] Howard W M, Fried L E, Souers P K.Kinetic modeling of non-ideal explosives with CHEETAH, DE200114716[R]. Livemore:LLNL,2001. [10] 魏贤凤, 龙新平, 韩勇. VLWR程序计算CHNO炸药爆轰性能碳相态的选择[J]. 含能材料, 2013, 21(5):604-608. WEI Xian-feng, LONG Xin-ping, HAN Yong. Selection of carbon phase in calculation of detonation performance by VLWR program for CHNO explosives[J]. Chinese Journal of Energetic Materials, 2013, 21(5):604-608. [11] 张为鹏, 毕福强, 王永顺,等. 1,1′-二羟基-5,5′-联四唑二羟胺盐理论爆速的计算[J]. 火炸药学报, 2015, 38(6):67-71. ZHANG Wei-peng, BI Fu-qiang, WANG Yong-shun, et al. Calculation of theory detonation velocity of dihydroxylammonium 5,5′-bistetrazole-1,1′-diolate [J]. Chinese Journal of Explosives & Propellants(Huozhayao Xuebao), 2015, 38(6):67-71. [12] 韦秉旭,陈寿如.用BKW规则和BKW程序计算乳化炸药爆轰产物的比较[J].湘潭师范学院学报(自然科学版),2003,25(4):50-54. WEI Bing-xu, CHEN Shou-ru.Comparison of detonation products of emulsion explosives computed with B-W regulation and BKW program[J].Journal of Xiangtan Normal University(Natural Science Edition), 2003, 25(4): 50-54. [13] 李德华.炸药爆轰参数、生成热及爆热的理论研究[D].成都:四川大学,2005. [14] Muhamed Suceska, How-Ghee Ang, Hay Yee Serene Chan.Study of the effect of covolumes in BKW equation of state on detonation properties of CHNO explosives[J].Propellants, Explosives,Pyrotechnics, 2013, 38: 103-112. [15] 韩早,王伯良.混合炸药爆速预报的新方法[J].爆炸与冲击,2014,34(4):421-426. HAN Zao, WANG Bo-liang.A new method for predicting detonation velocity of composite explosive[J].Explosion and Shock Waves, 2014, 34(4): 421-426. [16] 王小红,李晓杰,李瑞勇,等.特殊炸药的爆轰参数计算[J].高压物理学报,2013,27(1):119-124. WANG Xiao-hong, LI Xiao-jie, LI Rui-yong, et al.Calculation of detonation parameters of special explosives[J].Chinese Journal of High Pressure Physics, 2013, 27(1): 119-124. [17] 韦秉旭,吴雄,唐健军.用BKW状态方程计算乳化炸药爆轰参数的研究[J].爆破器材,2001,30(6):1-4. WEI Bing-xu, WU Xiong, TANG Jian-jun, et al.The calculation research of emulsion explosive detonation parameters with BKW equation[J].Explosive Materials, 2001, 30(6): 1-4. [18] 杜明燃,汪旭光,郭子如,等.爆轰产物组成和爆轰参数计算方法的理论研究[J].爆炸与冲击,2015,35(4):449-453. DU MING-ran, WANG Xu-guang, GUO Zi-ru, et al.Theoretical studies for calculating the detonation products and properties of explosives[J].Explosion and Shock Waves, 2015, 35(4): 449-453. [19] 何伟平, 黄菊, 刘晓静, 等. 基于多维空间的燃烧平衡产物组成的计算方法[J]. 火炸药学报, 2016, 39(4):46-50. HE Wei-ping, HUANG Ju, LIU Xiao-jing, et al. Calculation method of combustion equilibrium product compositions based on multidimensional space [J]. Chinese Journal of Explosives & Propellants(Huozhayao Xuebao),2016, 39(4):46-50. [20] Narwaria, Manish, Lin Wei-si.Objective image quality assessment based on support vector regression[J].Neurai Networks, 2012, 21(3): 515-519. [21] Bosch R, Smith J A.Separating hyperplanes and the authorship of the disputed federalist papers[J].American Mathematical Monthly, 1998, 105(7): 601-608. [22] 欧育湘, 王艳飞, 刘进全, 等. 近20年问世的5个新高能量密度化合物[J]. 化学通报, 2006, 69:1-7. OU Yu-xiang, WANG Yan-fei, LIU Jin-quan, et al. Five novel high energy density compounds synthesized in the latest 20 years[J]. Chemistry Bulletin, 2006, 69:1-7. [23] 欧育湘, 孟征, 刘进全. 高能量密度化合物CL-20应用研究进展[J]. 化工进展, 2007, 26(12):1690-1694. OU Yu-xiang, MENG Zheng, LIU Jin-quan. Review of the development of application technologies of CL-20[J]. Chemical Industry and Engineering Progress, 2007, 26(12):1690-1694. [24] 陈鲁英, 杨培进, 张林军, 等. CL-20炸药性能研究[J]. 火炸药学报, 2003, 26(3):65-67. CHEN Lu-ying, YANG Pei-jin, ZHANG Lin-jun, et al. Study of the performance of explosive CL-20[J]. Chinese Journal of Explosives & Propellants(Huozhayao Xuebao),2003, 26(3):65-67. [25] 项大林, 荣吉利, 李健, 等. 黑索今基含铝炸药的铝氧比对爆轰性能及其水下爆炸性能的影响[J]. 兵工学报, 2013, 34(1): 45-50. XIANG Da-lin, RONG Ji-li, LI Jian, et al. Effect of Al/O ratio on detonation performance and underwater explosion of RDX-based alumiized explosive[J]. Acta Armamentarii, 2013, 34(1): 45-50. Improved Algorithm of Detonation Products and Parameters Based on the BKW Equation of State HE Wei-ping1, HUANG Ju2, CHEN Hou-he3, LIU Xiao-jing1, WANG De-tang1,4 (1. School of Chemical Engineering,Xuzhou College of Industrial Technology,Xuzhou Jiangsu 221140, China;2. School of Chemistry & Chemical Engineering, Xuzhou Institute of Technology, Xuzhou Jiangsu 221111,China; 3. School of Chemical Engineering, Nanjing University of Science & Technology, Nanjng 210094,China; 4.Jiangsu Province Engineering Technology Research and Development Center of New Chemical Materials, Xuzhou College of Industrial Technology, Xuzhou Jiangsu 221140, China) To reduce the difficulty of predicting the detonation products and solving detonation parameters, the equilibrium compositions of detonation products were achieved by linear combination of the basic feasible solutions, which were obtained from the mass conservation equations; and the detonation parameters were further obtained based on equilibrium compositions. The major process was executed as follows: the basic feasible solutions were selected out by the principle of minimum free energy, and the initial solution was given by the principle of largest heat release. The equilibrium compositions of detonation products were linearly searched by uniting the initial solution with the basic feasible solutions, and the above-mentioned operation steps were completed by using self-made program. The parameters of the BKW equation of state were adjusted applying the linear support vector machine (SVM), and its main steps were introduced in detail. The detonation products and parameters of PETN, CL-20 and aluminized explosives were predicted with this method, and after parameter adjustment, it is found that the predicted results and the experimental ones are in better agreement. In comparison with the detonation experiment data of single compound, it is found out that when the BKW equation parameters are adjusted, the energetic materials with more similar percentage of gas fraction in detonation mass to the explosives predicted should be used as the training set of the LS-SVM model. If the detonation parameters of aluminized explosives are predicted, it should use the Al/O ratio close to measured explosive to train the SVM model. explosion mechanics; BKW equation of state; basic feasible solution; support vector machine;SVM; Gibbs free energy 10.14077/j.issn.1007-7812.2017.03.009 2016-09-01; 2017-01-04 徐州市科技计划社会发展项目(KC15SH064);徐州工业职业技术学院科技基金资助项目(XGY201607) 何伟平(1983-),男,硕士,讲师,从事含能材料理论计算研究。E-mail: 252927740@qq.com TJ55;O381 A 1007-7812(2017)03-0053-072 BKW状态方程的参数调整


3 算法验证及优化
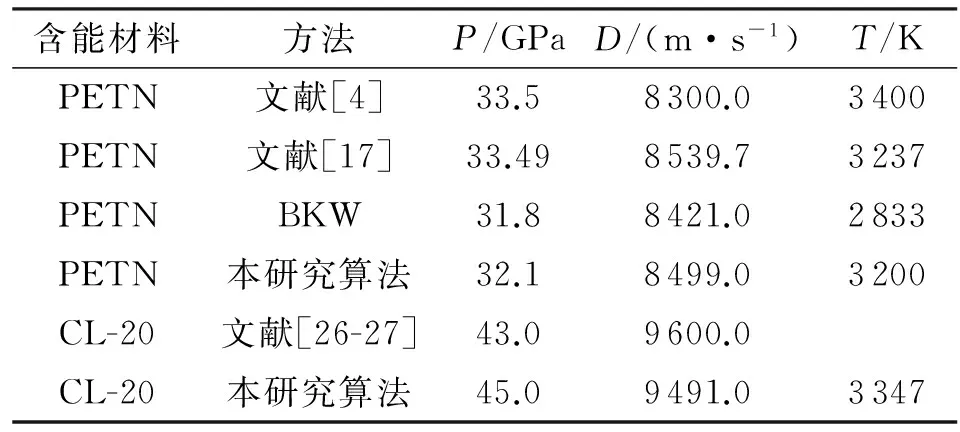

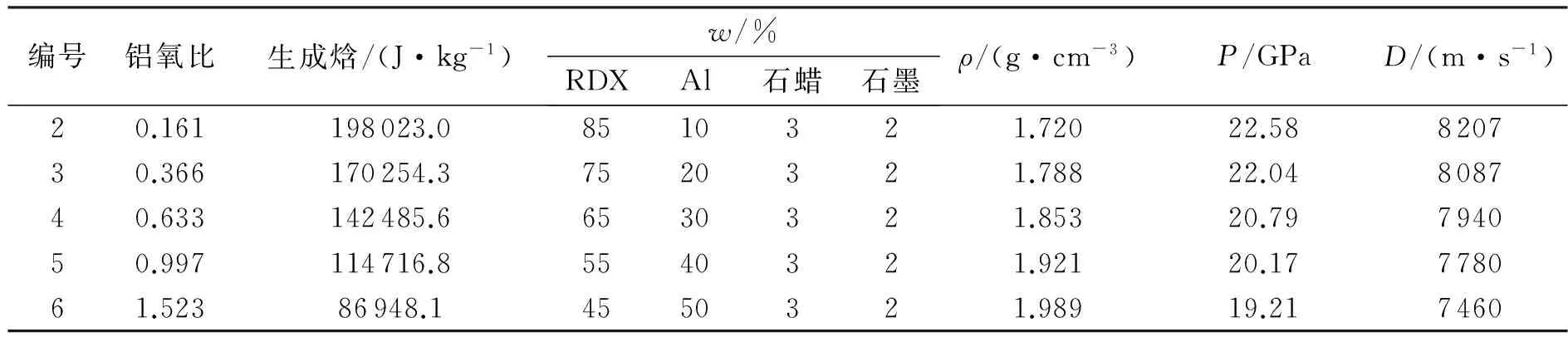

4 结 论

