双锥面熔体微分静电纺中电场分布的有限元分析

张艳萍， 张莉彦， 陈宏波， 杨卫民， 谭 晶， 李好义

(北京化工大学 机电工程学院, 北京 100029)

双锥面熔体微分静电纺中电场分布的有限元分析

张艳萍， 张莉彦， 陈宏波， 杨卫民， 谭 晶， 李好义

(北京化工大学 机电工程学院, 北京 100029)

为获得最佳的熔体微分静电纺丝结构参数，采用有限元分析软件ANSYS对多层锥面无针熔体微分静电纺丝中的电场分布进行模拟，分析了双锥面特征设计参数对纺丝尖端场强的影响，分别讨论了内圈直径和内圈伸出距离对内外圈纺丝尖端及纺丝路径场强分布的影响。ANSYS数值模拟结果表明：增加锥面层数会减弱最外圈纺丝尖端的电场强度；对于双锥面熔体纺丝装置，内锥面直径大小对纺丝尖端场强分布的影响不明显；当内锥面伸出距离增大时，内外圈纺丝尖端场强的差值先减小再增大；当内锥面直径为26 mm，内圈伸出距离为6 mm时，内外圈纺丝尖端电场强度分布最相似，能够保证内外锥面制备的纤维射流间距相同，实验结果和模拟结果一致。

熔体微分静电纺丝； 电场模拟； 双锥面； 纺丝尖端场强

静电纺丝技术是通过使带有电荷的高分子熔体或溶液在高压静电场中喷射、拉伸、劈裂、固化或者溶剂挥发，最终形成纤维状物质的过程，是一种有效制备连续纳米纤维的技术[1]。静电纺丝可以分为溶液静电纺丝和熔体静电纺丝。由于熔体静电纺丝不使用溶剂，是一种绿色制造技术，而且不存在溶剂挥发，生产效率高，因而是目前静电纺丝研究重点之一。传统的单针喷头静电纺丝设备的生产效率极低，限制了静电纺丝纳米纤维产业化应用，所以研究改进无针多射流电纺技术是提高纤维生产效率的重要途径[2]。肖桂花等[3]综述了流体微分静电纺丝喷头设计的基本原理和研究进展；Komarek 等[4]提出了一种狭缝式熔体无针静电纺丝装置，可以避免针头堵塞，提高纺丝效率，但要满足微流量均匀分布，流道设计比较复杂；Fang 等[5]将盘式溶液无针静电纺丝技术应用到熔体静电纺丝装置上，制备出最细的一组样品为(400±290)nm，但由于该装置对熔体黏度要求十分苛刻，限制了其批量化稳定可控生产；杨卫民等[6]基于高分子先进制造微积分思想，提出熔体微分静电纺丝技术，并搭建了无针熔体静电纺丝产业化线。

在无针静电纺丝过程中，作用于各射流的电场力是主要驱动力，工作电场的强度大小及方向直接影响着泰勒锥及射流的分布及变形强度，并间接决定纤维的直径分布，因此通过电场模拟分析工作电场来优化无针电纺装置可以有效获得最佳纺丝装置的设计参数。现已发表的文献[7-8]主要是对单针溶液电纺进行电场模拟分析，通过改变输入电压、喷丝管直径和长度以及喷丝管与接收板的距离等设计参数和工艺参数来获得目标纤维特征参数；文献[9-10]主要研究了多射流静电纺丝装置电场分布的影响因素；也有一些学者对射流纺丝过程进行了模拟分析，贾琳[11]应用POLYFLOW软件模拟了在不同拉伸力条件下，电纺稳定段射流的拉伸形态。

综上所述，本文提出双锥面无针熔体微分静电纺丝装置，增加锥面层数一方面可以有效提高纺丝效率，另一方面相比多喷头装置结构更加紧凑，有利于扩大规模生产。通过模拟分析内圈直径和内圈伸出距离对内外圈纺丝尖端及纺丝路径电场强度分布情况的影响，得到最优工作电场分布形态，为进行双锥面熔体静电纺丝装置的总体结构优化设计提供理论参考，并且通过实验考察纺丝效果。

1 双锥面熔体微分静电纺丝装置

熔体微分静电纺丝的原理是微流量熔体高温熔融后在微分喷头表面展薄形成周向分布的瀑布流，在高压静电场的电场力作用下，克服其自身以及自身和喷头介质之间的表面张力，自组织形成多个均布的泰勒锥。随着电压的增大，进而形成多股带电喷射流，熔体射流在喷射过程中由于热量散失而固化，最终到达接收装置形成超细纤维，直径一般在数十纳米到微米之间[12-13]。区别于传统熔体静电纺丝喷头，本装置采用双锥面结构，如图1所示，内外圈纺丝尖端在高压静电作用下同时形成多股喷射流，有效提高了纺丝效率。本文主要通过改变内圈直径和内圈伸出距离来模拟分析模型的工作电场，以获得最佳结构参数。

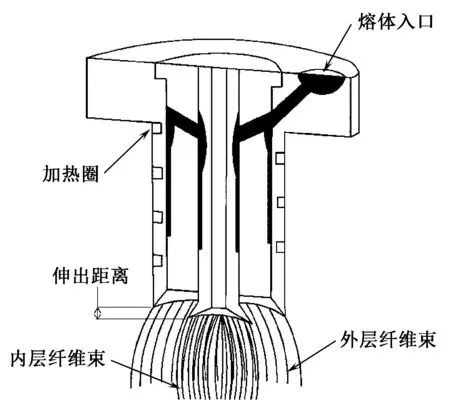
图1 双锥面熔体微分静电纺丝装置结构图Fig.1 Schematic of double cone needleless melt differential electrospinning device

2 工作电场模拟

2.1 模型求解参数

本文采用ANSYS有限元分析软件来进行模拟仿真，首先建立双锥面喷头的三维模型，用空气包覆模型与喷头模型进行布尔减法运算，得到求解模型，然后对模型定义材料、网格划分及施加边界条件后进行求解运算。图2示出双锥面熔体微分静电纺丝装置的几何模型图，具体结构参数为：外圈锥面喷头直径52 mm，内圈锥面喷头直径26～34 mm，内圈伸出距离0～10 mm，喷头长度100 mm，接收板尺寸220 mm，接收板距喷头锥面距离150 mm，模拟纺丝电压50 kV。在熔体静电纺丝中，为避免加热电控系统和高压静电之间的干扰，一般采用喷头电极接地，接收板电极接高压正极的反纺接电方式。正纺与反纺的模拟结果相同，只是电场强度方向相反，本文采用了反纺接电方式。

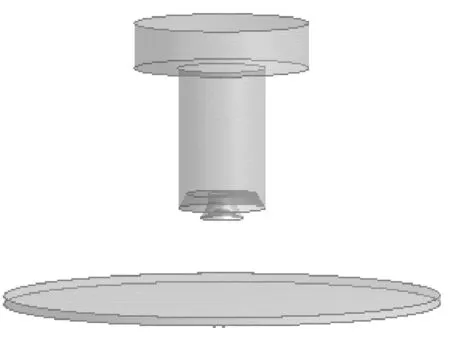
图2 双锥面熔体微分静电纺丝装置的几何模型图Fig.2 Simulation modeling of double cone needleless melt differential electrospinning device

2.2 模拟方法

双锥面熔体静电纺丝的过程中，周向均匀分布在纺丝尖端的泰勒锥在电场力作用下形成多股喷射流，经过拉伸细化、冷却固化最终落到接收板形成纤维。因此，为保证内外圈纤维直径分布均匀，其关键是要实现内外圈纺丝尖端电场强度分布相似。图3示出模拟过程中提取的计算路径图，其中路径1和路径2分别为外圈与内圈纺丝尖端“edge”路径，分别研究了内圈锥面直径与内圈伸出距离的改变对选取路径的场强分布的影响。对于熔体静电纺丝，纤维细化只能靠静电牵伸作用，分析纤维路径上的电场强度分布规律对实验过程参数控制具有指导意义。因此提取了图3中外圈纤维路径3，参考实际纺丝效果，纤维落点选择为到接收板时向外偏离1.5 cm。

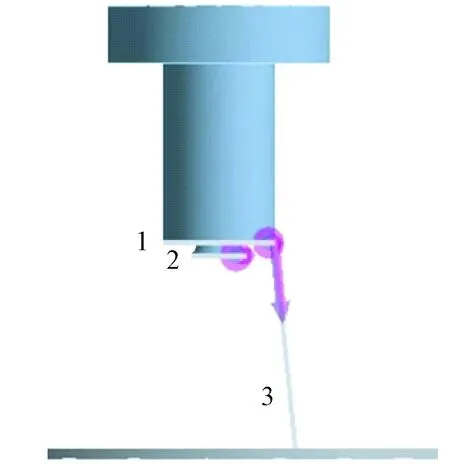
图3 模型路径图Fig.3 Images of selected path

3 结果分析与讨论

3.1 锥面层数的影响

大多熔体纺丝喷头为单层，纺丝效率较低，为提高纤维产量，一般采用增加喷头数量的方法，但会使得装置结构复杂，增加能耗和设备占地面积；为了提高单位纺丝模块的纺丝效率，本装置中则通过增加内锥面层数来增加纤维产量，但要选取合理的结构参数使得每层锥面纺丝尖端的电场强度分布均匀。通过模拟对比单层、双层和3层锥面熔体纺丝模型，发现增加锥面层数会减弱最外圈纺丝尖端的电场强度，而且内外层锥面纺丝尖端的场强分布不均匀，模拟数值结果如图4所示。对于3层锥面无针熔体微分静电纺丝装置，其内外圈纺丝尖端的电场强度分布与双锥面装置相似，继续增加锥面层数对纺丝尖端场强分布影响不明显，因此采用双锥面无针熔体微分静电纺丝装置建立有限元模型，来模拟装置设计参数对内外圈纺丝尖端及多射流路径上场强分布的影响。

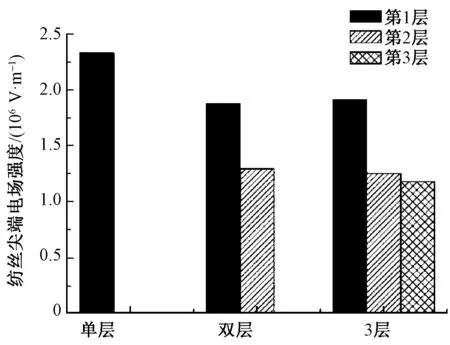
图4 多层锥面纺丝尖端场强分布Fig.4 Electric field intensity distribution of multilayer cone spinning edge

3.2 内圈直径对纺丝尖端场强的影响

双锥面无针熔体微分静电纺丝装置由于其内外圈纺丝尖端可以同时形成喷射流，纺丝效率成倍增加，但内锥面尺寸会影响内外圈纺丝尖端场强分布，如图4所示，内圈纺丝尖端周向场强小于外圈。为使得最终纤维直径和形貌均匀，内外圈纺丝尖端电场强度分布要尽可能相似。考虑到喷头加工的可行性和纺丝工艺过程，考察了双锥面无针熔体微分静电纺丝装置，外圈直径固定为52 mm，内圈直径分别为26、28、30、32、34 mm时，内外圈纺丝尖端场强分布情况。采用ANSYS电场模拟里面的“edge”方法提取出了内外圈纺丝尖端，如图3中的路径1和路径2，在上述5种内圈直径下的场强模拟数值，由于网格划分误差，纺丝尖端周向场强分布在一定范围内波动，因此分别取内外圈提取路径上的场强平均值，外圈和内圈纺丝尖端场强的平均值以及内外圈场强的差值都基本不变，说明内圈直径大小对纺丝尖端场强分布影响不明显，如图5所示。

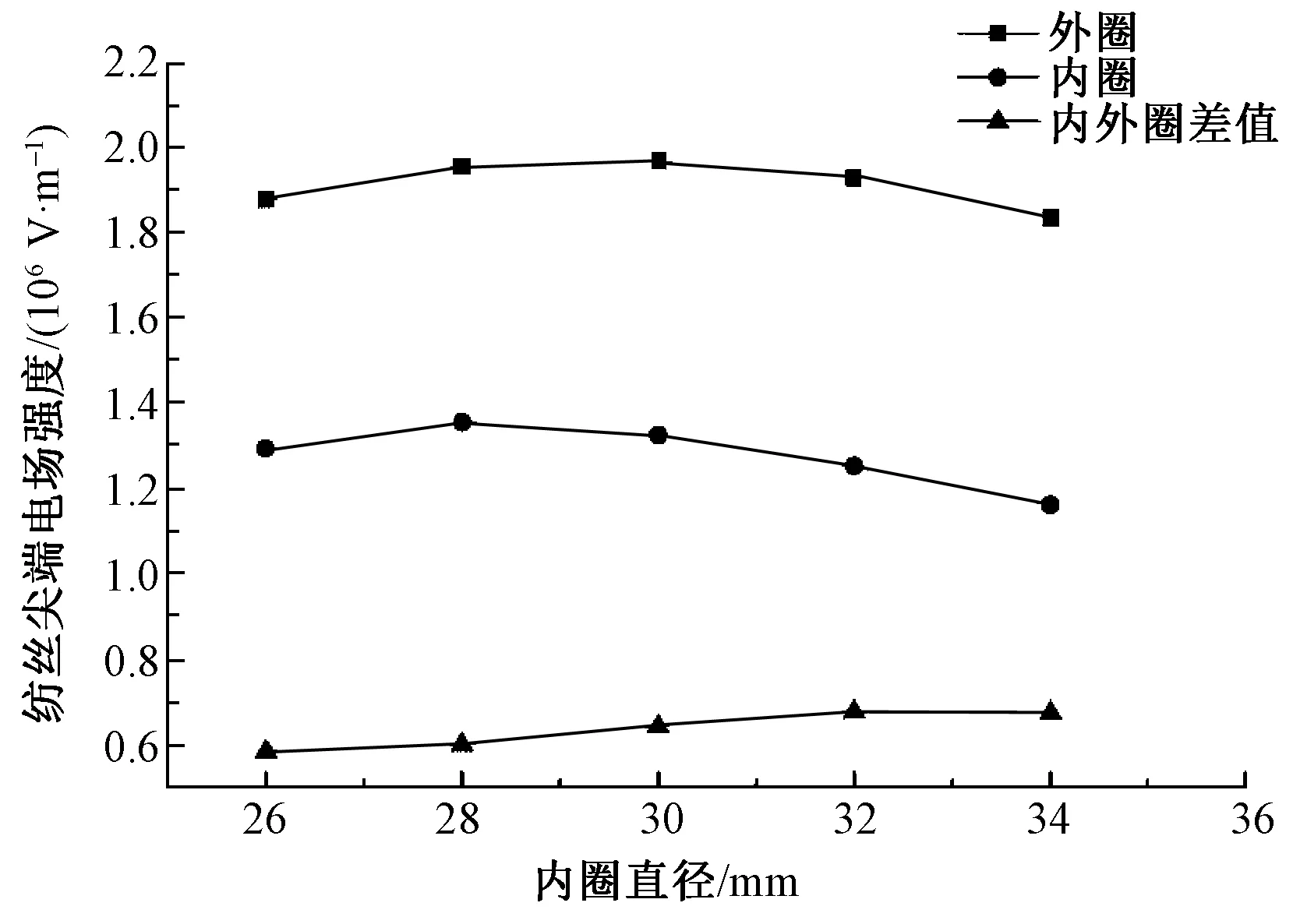
图5 内外圈纺丝尖端场强大小变化趋势图Fig.5 Electric field changes of inner and outer cone spinning edge

3.3 内圈伸出距离对纺丝尖端场强的影响

电场强度的大小随喷头与接收板间距离的减小而增大，为使内外圈纺丝尖端电场强度分布相似，可以将内圈伸出适当的距离。分别模拟了内圈直径为26 mm，内圈伸出距离为0、2、4、6、8、10 mm时的纺丝尖端场强分布情况，其周向平均值变化趋势如图6所示。从图中可看出，随着内圈伸出距离的增大，内外圈纺丝尖端场强平均值差值越来越小，当内圈伸出距离为6 mm时，内外圈纺丝尖端周向场强平均值基本相同。当内圈伸出距离继续增大时，内圈纺丝尖端周向场强平均值大于外圈，且内外圈场强差值随伸出距离的增加而增大。图7为内圈伸出距离6 mm时的电场强度分布云图，可看出电场强度最大值出现在喷头尖端附近，而且内外圈尖端场强分布相似。

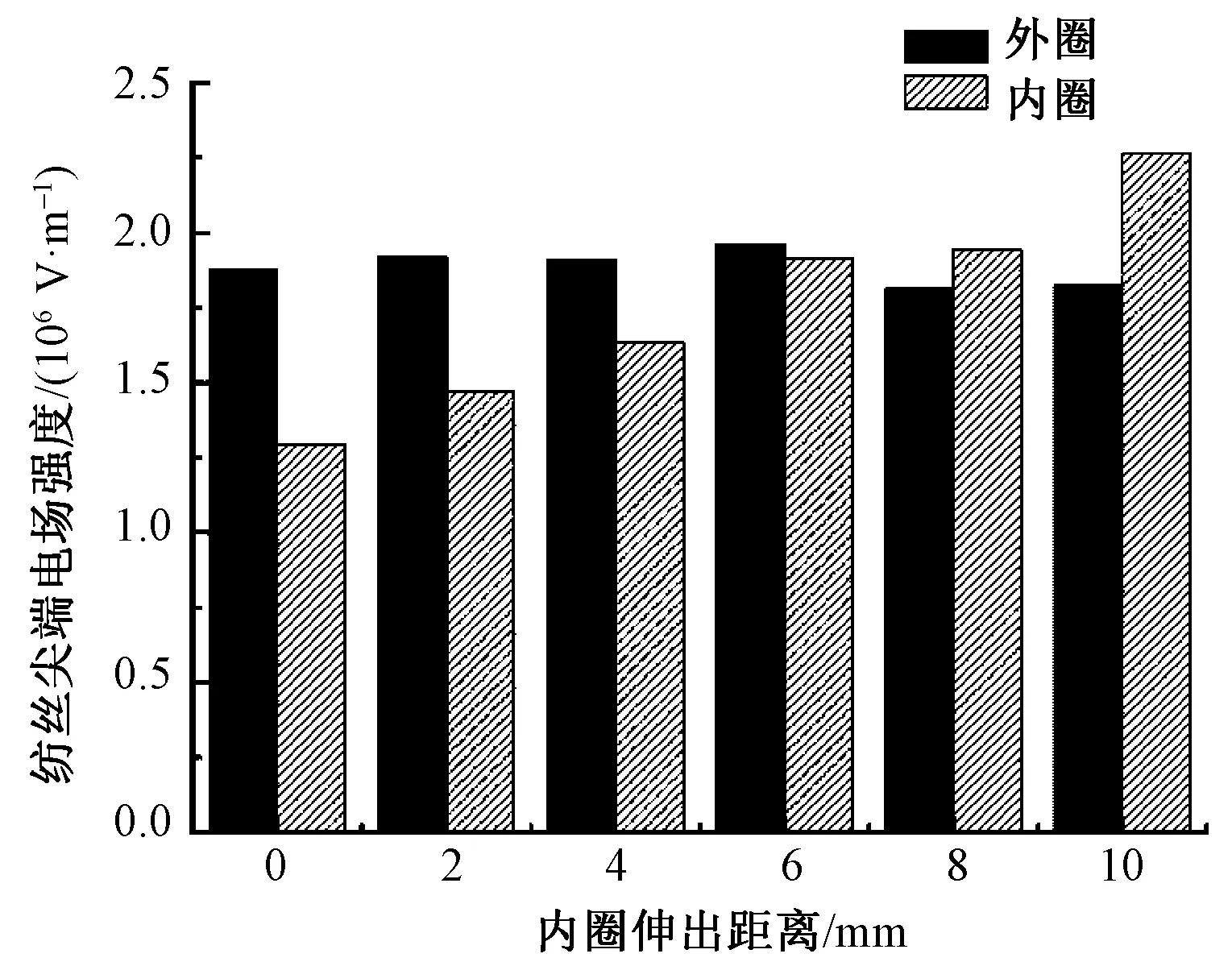
图6 内外圈纺丝尖端场强变化趋势图Fig.6 Electric field changes of inner and outer cone spinning edge

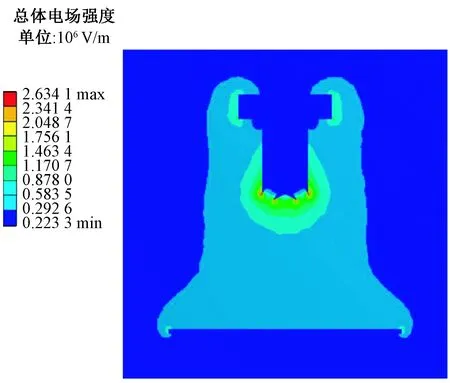
图7 电场强度分布云图Fig.7 Contour graph of electric field intensity distribution

3.4 多射流路径上场强分布

取图3中的外圈类纤维路径3计算电场强度，模拟结果如图8所示。由图可见射流路径上的最大场强出现在纺丝尖端，而且在距离尖端的一小段距离内，场强值急剧下降后趋于平缓，从图7的电场强度分布云图的颜色变化也可以看出电场强度的变化趋势。该结果与段宏伟[14]等模拟单针溶液静电纺丝装置的结果一致。

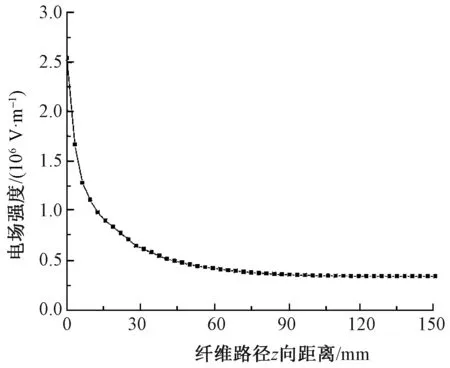
图8 纤维路径的场强分布Fig.8 Electric field intensity distribution of path edge

3.5 双锥面熔体微分静电纺丝实验

在无针静电纺丝过程中，射流间距是指两相邻泰勒锥尖端之间的距离，其大小直接影响单位纺丝模块的纤维产量。Lukas等[15]通过理论分析给出了溶液无针静电纺丝中射流间距的计算公式：

式中：λ为平均射流间距，mm；γ为溶液的表面张力，N/m；ε为空气介电常数，F/m；E0为电场强度大小，V/m；ρ为溶液密度，kg/m3；g为重力加速度，m/s2。根据公式可知，平均射流间距λ随着电场强度E0的增大而减小。李好义等[16]通过模拟和实验证明该射流间距计算公式也同样适用于无针熔体微分静电纺丝，因此，通过测定纺丝实验中射流间距的大小可验证电场模拟结果。

根据模拟得出的最佳参数，设计了内圈直径为26mm的双锥面无针熔体微分纺丝装置，内圈伸出距离可调。实验参数选择为：纺丝距离150mm，电压50kV，喷头温度240 ℃。实验原材料：上海伊士通新材料有限公司的聚丙烯(PP6520)粒料，熔体流动指数(MFI)为2 000g/10min，相对分子质量为50 000，密度为0.91g/cm3。

图9示出内圈伸出距离为6mm时的纺丝实验照片图，使用相机(Cannon600D)在6倍焦距条件下拍摄，然后将获得的照片进行射流根数的平均计算获取射流间距，射流间距的计算公式为λ=πD/n，其中D为微分喷头的尖端直径，n为通过计数拍得相片上的多射流根数获得[15]。

图9 纺丝实验照片图Fig.9 Photos of melt differential electrospinning

经测定，外圈纤维射流间距为2.63 mm，内圈纤维射流间距为2.72 mm。内外圈射流在纺丝尖端周向分布基本一致，表明内外圈尖端电场分布均匀，与图7的电场模拟结果一致。

4 结 论

1)对于多层锥面无针熔体微分电纺装置，增加锥面层数会减弱最外圈纺丝尖端的电场强度，而且内外层锥面纺丝尖端的场强分布不均匀。

2)双锥面无针熔体微分静电纺装置中，内圈直径大小对纺丝尖端场强分布的影响不明显。

3)内锥面直径为26 mm的双锥面无针熔体微分静电纺装置中，随着内圈伸出距离的增大，内外圈纺丝尖端场强平均值的差值先减小后增大，当内圈伸出距离6 mm时，内外圈纺丝尖端纤维射流间距相同，表明内外圈纺丝尖端电场强度分布最相似。

FZXB

[ 1] 王策, 卢晓峰. 有机纳米功能材料:高压静电纺丝技术与纳米纤维[M]. 北京:科学出版社, 2011:4-28. WANG Ce, LU Xiaofeng. Organic Nano-Scale Functional Materials : High Voltage Electrospinning Technology and Nano Fiber [M]. Beijing: Science Press, 2011:4-28.

[ 2] 田龙, 李杰, 潘志娟. 多射流静电纺丝技术的研究现状[J]. 纺织学报, 2013, 34(9): 150-155. TIAN Long, LI Jie, PAN Zhijuan, et al. Research status of multi-jet electrospinning technology[J]. Journal of Textile Research, 2013, 34(9): 150-155.

[ 3] 肖桂花, 李好义, 李小虎，等. 流体微分静电纺丝喷头设计的研究进展[J]. 纺织学报, 2014, 35(12): 153-158. XIAO Guihua, LI Haoyi, LI Xiaohu, et al. Research process of fluid differential electrostatic spinning nozzle design[J]. Journal of Textile Research, 2014, 35(12): 153-158.

[ 4] KOMAREK M, MARTINOVA L. Design and evaluation of melt-electrospinning eletrodes [C]//Proceeding of the Conference NaNOCON 2010. Olomouc: [s.n],2010: 12-14.

[ 5] FANG J, ZHANG L, SUTTON D, et al. Needleless melt-electrospinning of polypropylene nanofibres[J]. Journal of Nanomaterials, DOI:10.1155/2013/382639.

[ 6] 杨卫民, 钟祥烽, 李好义， 等. 一种熔体微分静电纺丝喷头:中国, 201310159570.0[P]. 2013-07-31. YANG Weimin, ZHANG Xiangfeng, LI Haoyi, et al. A melt differential electrospinning nozzle: China, 201310159570.0[P]. 2013-07-31.

[ 7] 王文, 顾平道, 张蒙, 等. 单针头静电纺丝电场强度影响因素有限元分析[J]. 合成纤维, 2015 (9): 35-39. WANG Wen, GU Pingdao, ZHANG Meng, et al. Finite elment analysis of factors affecting electric field intensity on single needle electrospinning[J]. Synthetic Fiber in China, 2015 (9): 35-39.

[ 8] 庄昌明, 曾泳春. 电场均匀性对单孔静电纺丝的影响[J]. 纺织器材, 2014, 41(2): 67-73. ZHUANG Changming, ZENG Yongchun. The uniformity of electric field on the single holed static spinning[J]. Textile Accessories, 2014, 41(2):67-73.

[ 9] 陈威亚, 刘延波, 王洋知， 等. 多针头静电纺丝过程中电场强度与分布的有限元分析[J]. 纺织学报, 2014, 35(6): 1-6. CHEN Weiya, LIU Yanbo, WANG Yangzhi, et al. Finite element analysis on electric field intensity and distribution during multi-needle electrospinning process[J]. Journal of Textile Research, 2014, 35(6): 1-6.

[10] 陈威亚, 刘延波, 张泽茹， 等. 多针头静电纺场强改善的有限元分析[J]. 纺织学报, 2014, 35(4): 21-31. CHEN Weiya, LIU Yanbo, ZHANG Zeru, et al. Finite element analysis of improvement of field intensity in multi-needle electrospinning[J]. Journal of Textile Research, 2014, 35(4): 21-31.

[11] 贾琳. 静电纺 PVA 纳米纤维射流的拉伸研究与模拟初探[D]. 上海: 东华大学, 2009: 69-82. JIA Lin. Study on the jet stretching of electrospinning polyvingylalcohol(PVA) nanofibers and numerical simulation[D]. Shanghai: Donghua University, 2009: 69-82.

[12] 杨卫民, 李好义, 吴卫逢，等. 熔体静电纺丝技术研究进展[J]. 北京化工大学学报, 2014, 41(4): 1-13. YANG Weimin, LI Haoyi, WU Weifeng, et al. Research advances in melt electrospinning[J]. Journal of Beijing University of Chemical Technology, 2014, 41(4):1-13.

[13] 钟祥烽, 李好义, 陈宏波，等. 内锥面喷头熔体静电纺丝工艺参数对纤维直径的影响[J]. 塑料, 2014, 43(3): 89-93. ZHONG Xiangfeng, LI Haoyi, Chen Hongbo, et al. Influence of process parameers on fiber diameter in melt electrospinning with inner cone nozzle[J]. Plastics, 2014, 43(3): 89-93.

[14] 段宏伟, 毕淑娟, 王延福, 等. 高压静电纺丝机工作电场 FEM 分析[J]. 哈尔滨商业大学学报(自然科学版), 2009 (4): 461-463. DUAN Hongwei, BI Shujuan, WANG Yanfu, et al. FEM analysis on working electrostatic field of high voltage electrospinning machine[J]. Journal of Harbin University of Commerce (Natural Science Edition), 2009, 25(4):461-463.

[15] LUKAS D, SARKAR A, POKORNY P. Self-organization of jets in electrospinning from free liquid surface: a generalized approach[J]. Journal of Applied Physics, DOI:10.1063/1.2907967.

[16] 李好义. 熔体微分静电纺丝原理、方法与设备[D]. 北京: 北京化工大学, 2014: 43-50. LI Haoyi. Principle, method, and equipment of melt differential electrospinning[D]. Beijing: Beijing University of Chemical Technology, 2014: 40-60.

Finite element analysis on electric field distribution in double cone melt differential electrospinning

ZHANG Yanping, ZHANG Liyan, CHEN Hongbo, YANG Weimin, TAN Jing, LI Haoyi

(CollegeofMechanicalandElectricalEngineering,BeijingUniversityofChemicalTechnology,Beijing100029,China)

In order to obtain optimized structural parameters of melt differential electrospining, finite element analysis software (ANSYS) was employed to simulate and analyze the distribution of the electric field intensity in multiple cone needleless melt differential electrospinning. The influence of design parameters on the electric field intensity was analyzed. The effect of inner diameter and extend distance on the electric field intensity distribution of spinning edge and spinning path was discussed respectively. The results indicate that the electric field intensity of the spinning edge was weakened with the increasing cone number, and for double cone needle-free melt differential electrospinning, the influence of inner diameter size on electric field intensity distribution of spinning edge is not obvious. While the extend distance of inner cone increase gradually, the difference value of electric filed intensity between inner and outer cone is found to decrease firstly and then increase. In particular, the electric filed intensity distribution of inner and outer cone is the most similar and the jet spacing of inner and outer cone is almost identical when the inner cone diameter is 26 mm, and inner extend distance is 6 mm. The experimental results are consistent with the simulation results.

melt differential electrospinning; electric field simulation; double cone; electric field intensity of spinning edge

10.13475/j.fzxb.20160503306

2016-05-16

2017-03-13

国家自然科学基金项目(51603009)；国家重点研发计划项目(2016YFB0302002)

张艳萍(1992—)，女，硕士生。主要研究方向为溶液熔体静电纺丝工艺。李好义，通信作者，E-mail：15001276730@163.com。

TQ 340.14

A