无尾鸭式布局无人机稳定特性研究

张喆　尤俊彬　华艺欣

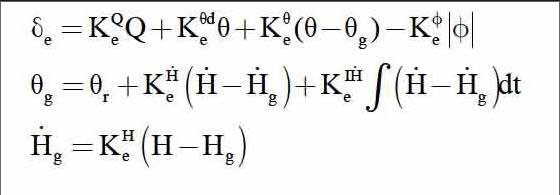
摘 要：针对一种新的飞翼式气动布局无人机，设计了一种常规构型的飞行控制律。在飞行试验中，发现飞机横向稳定特性较差，为了弄清这一问题出现的原因，并改进控制律，充分分析仿真计算与真实飞行一些细微差别的基础上，设计了一种基于线性调频Z变换的数据处理方法，该方法可在飞行试验中对各轴的稳定特性进行有效的评估。通过大量试验数据的分析处理，得出了横向稳定性差是由于横向回路增益参数设计不合理引起的结论，在该结论指导下对控制律进行调参，在后续试飞中取得良好的效果。

关键词：飞翼；稳定性；研究

1 概述

随着近年来我国航空技术的发展，小型飞翼式布局无人机得到了越来越广泛的应用。该布局的主要优点是：

低Radar-Cross Section（雷达散射截面积，简称RCS）特性，可在试飞工作中作为低隐身特性飞机作为目标机，开展雷达系统试验；良好的升阻特性，在结构设计方面可减轻全机重量，提升任务载荷重量。

无尾鸭式布局是一种改良飞翼气动布局形式，配有鸭翼以进一步提高飞机升阻特性。由于取消了平尾，而翼尖垂尾距重心的力臂较短，故纵向与航向的本体稳定特性低于常规布局飞机，这给飞控系统的设计工作带来挑战。

由于该气动布局飞机的本体稳定性较差，需要利用自动飞控系统进行增稳控制。才能使飞机在空中正常的飞行。因此，在飞行试验中，对设计的飞控系统进行稳定性分析，对于控制律的改进和飞控系统评定具有重要意义。这种试验最早是在NASA的开展的，并在多种验证机的试飞工作中得到应用。包括：X-36验证机[1]、X-38验证机[2]、X45、X48等飞翼式布局无人验证机等[3][4]。

在国内，北京航空航天大学王立新、李林、马超、李淼[5]-[10]等人对飞翼布局飞机的稳定特性、飞行品质、控制器设计方法等进行了广泛深入的研究，给出了飞翼布局飞机增稳控制的理论方法。本文在这些研究成果的基础上，设计了一种计算机仿真计算方法，这种方法可对飞翼布局飞机在飞行试验中的稳定性进行评估，给出定量的结果。达到了国外航空强国的同等技术水平。

2 研究对象

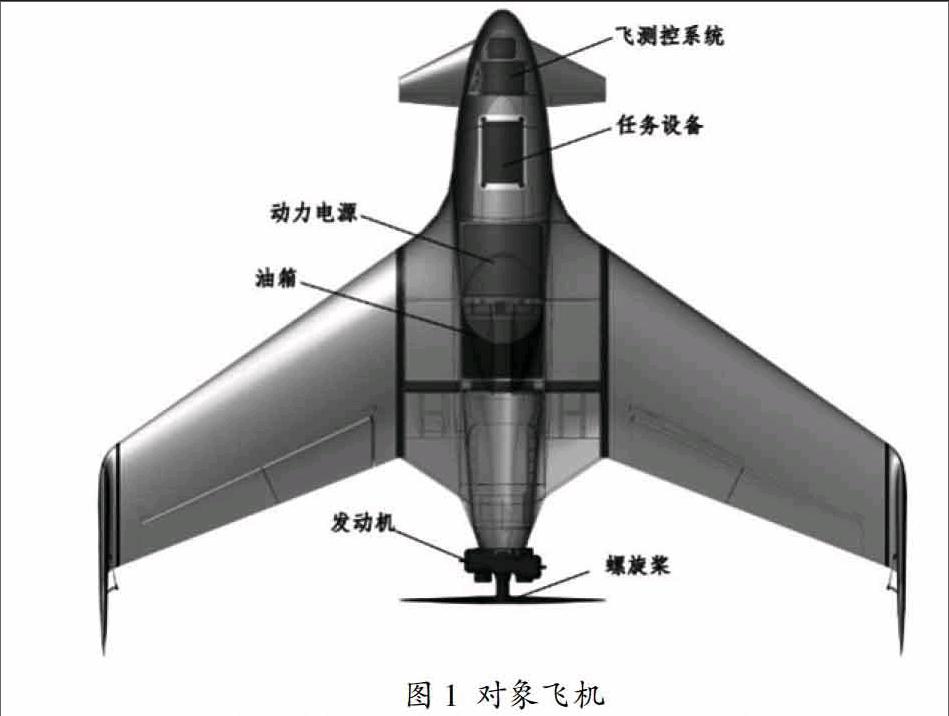
对象飞机如图1所示。为一种典型的无尾鸭式布局无人机，采用中等展弦比的飞翼式布局，机身前方配有小型鸭翼。发动机安装在机身尾部，采用后推式动力。

该机有2组飞行控制面，包括升降副翼、方向舵。其中，当升降副翼同向偏转时，可进行俯仰方向控制飞机本体，当差动时，可进行滚转方向控制。针对该构型本体动力学特点，结合实际飞行中的任务要求，设计了一种基于经典控制理论的飞行控制律。

在控制律调参时，参照有人驾驶飞机飞行品质规范MIL-STD-1797A的要求，为该机设计了期望的品质参数以供控制律调参使用。如表1和表2所示。表1给出了巡航状态（空速Va=27m/s，高度2000m）的纵向回路设计结果，表2给出了横航向回路设计结果。

仿真研究发现，前述控制律的稳定性、快速响应特性均有良好的效果，可以快速消除扰动，且超调量较小。

飞行试验验证在一个空域较为有限的小型机场进行。该机场为山区机场，跑道两侧均为狭长山脉，常年气流扰动情况复杂。在试飞当天，有较强的大气紊流活动，最大风速大于9m/s。该无人机在飞行试验时的航迹如图2所示。飞机进行顺时针飞行。由于大气扰动的影响，在盘旋飞行时，每圈的飞行航迹没有完全重合。

图3为稳定平飞时的纵向响应曲线，由该图可以看出，纵向稳定性较好，在较强的气流扰动作用下（迎角变化剧烈），俯仰角变化范围为0.7°至3.3°。

图4为横向响应，从曲线可以看出，横向稳定性较差，滚转角持续性振荡，振荡幅值为+5°至-7°，需要改进控制律解决该问题。

3 问题分析及改进方法

3.1 问题分析

对该无人机的飞控系统稳定进行分析。如图5所示。

其中作动器模型为如图6。

图7、图8为滚转轴、俯仰轴的频响特性。

在从数据处理结果可以看出，滚转轴、俯仰轴的稳定裕度均满足幅值裕度6dB、相位裕度45°的要求。

进一步分析，仿真时作动器、传感器模型是基于线性模型的。认为滚转轴在仿真时稳定性满足要求，在实际飞行中稳定性不足的原因是：传感器、作动器等飞控系统设备的动态响应模型与真实情况中差异性很大，造成仿真分析的结果可信性不足。

3.2 解決问题的方法

为解决无人机在实际飞行中滚转轴稳定性不足，在强气流扰动下振荡幅值较大的问题，应在飞行中对该无人机的闭环系统稳定性进行试验，为控制律调参提供依据。

为得到各轴准确的频响特性细心，应进行频域辨识。完整的频域辨识流程如图9所示。试验数据经过多变量谱分析和规整后得到频率响应矩阵，由该矩阵即可对选定的输入/输出对辨识其传递函数模型。

本文主要采用线性调频Z变换技术（简称CZT变换）将时间历程数据转换成频率响应序列，当输入、输出的频率响应确定后，进一步得到系统的伯德图。

CZT能在单位圆弧上以很高的精度确定频率响应，具有高度的灵活性，尤其适合于从飞行试验数据中辨识频率响应。CZT具有以下特点：（1）CZT中，频率点的数量N可以独立于时间历程数据点数L而单独选取，仅需满足条件N？燮L且N+L是2的整数幂次方。CZT相对于FFT需要的条件宽松得多，一般程序中（包括MATLAB），FFT要求N=L，并且N和L都是2的整数幂次方。（2）CZT的N个频率点可以分布在单位圆的任意弧段上（这就是说，可以仅分布在感兴趣的频段），而不是像FFT一样分布在整个单位圆频率范围。以50赫兹采样率采集的20.48秒时间历程数据为例，窗口宽为L=1024（Twin=20.48s）。FFT得到的频率响应为均匀频率分辨率△f=1/20.48=0.0488Hz。频率响应包含N/2=1024/2=512个频率点，从fmin=1/20.48=0.0488Hz到fmax=fs/2=50/2=25Hz均匀分布。然而，典型情况下操纵品质分析应用中感兴趣的频率范围（以及合适激励信号的频率范围）是0.3-12rad/s（即0.0478-1.910Hz），这个范围仅仅包含了39个频率点，因此整个1024个频点中大部分浪费了。对CZT，计算结果能产生相同数量的频率点（1024个），但这些频率点可以只分布在0.3-12rad/s的范围，这等于将频率分辨率提高到了原来27倍，达到△f=（13-0.3）/（2π·1024）=0.00182Hz。（3）CZT有助于减小旁瓣泄漏或者数值污染造成的影响，和FFT相比具有更高的精度。

CZT的这三个重要特性为选取采样频率、窗口宽度、频率分辨率提供了更大的灵活性，提高了飞行试验数据分析中频率响应的精度。

3.3 扫频激励试验

本文稳定性边界测量所使用的输入和输出信号在图10中给出了说明。对于每一个轴，选择相应的输入/输出信号，频率响应特性就可以代表开环系统的传递函数。当扫频输入被加入到每一个轴上时，误差信号就产生了。输出信号的频率响应到误差信号就代表了给定轴的开环传递函数。

周期性的扫频输入一般会持续30秒，覆盖1.0到60弧度每秒的频率范围。所有的输入都是计算机生成的。设计的输入信号是用来激励一个刚性飞机动态特性的，激励时飞机保持在配平状态。为了获得合理的低频响应，而不偏离配平状态，就需要非常小的低频输入。

图11为滚转轴扫频试验时的响应曲线，其中黑色线是总误差信号，红色曲线是总反馈信号。

4 飞行试验结果及分析

4.1 数据处理结果

利用线性调频Z变换，得到的滚转轴、俯仰轴频率响应特性如图12、13所示。

从试验结果分析，滚转轴的幅值裕度为8.7dB，相位裕度为11.5°，远低于仿真计算时的系统稳定裕度，这就不难解释在飞行试验中为何滚转轴稳定性不足，在强风扰条件下振荡幅值较大的现象。

而俯仰轴的试验数据结果表明，该回路闭环系统稳定性仍满足6dB，45°的稳定裕度要求，实际飞行中该回路也具有良好的稳定性，振荡幅值较小。

4.2 控制律参数改进及试验验证

将滚转轴主回路的增益进行调整，满足闭环系统稳定裕度的要求。滚转轴的频响特性如图14所示。

图15是改进增益后的横向响应时间历程曲线，结果表明，滚转角振荡幅值为-2°～-9°，优于改进前的稳定性。同时，控制精度满足飞行任务的要求。

5 結束语

本文通过频域辨识方法，改进了小型低RCS无人机的控制器性能，其中重点研究了以下问题：（1）中等展弦比飞翼布局无人机的控制器设计及飞行试验验证。（2）根据飞行试验数据，分析滚转轴稳定性差、振荡幅值大产生的原因。在飞行试验中利用扫频激励分析闭环系统稳定性，开发一种基于线性调频Z变换方法的数据处理技术得到各轴的频响特性。（3）对滚转轴的控制增益进行改进，使得系统既满足稳定性要求，同时有良好的控制精度。

参考文献

[1]Dwight L， Balough. Determination of X-36 stability margins using real-time frequency response techniques， AIAA-98-4154[R]. Reston：AIAA，1998

[2]John T.Bosworth and Susan J.Stachowiak. Real-Time stability margin measurements for X-38 robustness analysis， NASA/TP-2005-212856[R].NASA Dryden flight research center， Edwards， California，2005.

[3]Kevin A.Wise. X-45 Program overview and flight test status， AIAA-2003-6645[R].Reston：AIAA，2005.

[4]Chirstopher D.Regan. In-Flight stability anslysis of the X-48B aircraft， AIAA-2008-6571[R]. Reston：AIAA，2008.

[5]李林，马超，王立新.小展弦比飞翼布局飞机稳定性分析[J].航空学报，2007，28（6）：1312-1317.

[6]李淼，王立新，黄成涛.舵面特性对飞翼构型作战飞机短周期品质的影响[J].航空学报，2009，30（11）：2059-2065.

[7]李林，王立新.小展弦比飞翼布局作战飞机偏航轴飞行品质评定[J].航空学报，2009，30（6）：972-978

[8]李林，马超，王立新.大展弦比飞翼构型的横航向操纵特性[J].北京航空航天大学学报，2007，33（10）：1186-1190.

[9]马超，王立新.飞翼布局作战飞机起降特性分析[J].北京航空航天大学学报，2009，35（4）：429-433.

[10]王立新，李林.小展弦比飞翼战机滚转轴操纵效能需求特性[J].北京航空航天大学学报，2009，35（8）：909-912.

作者简介：尤俊彬（1990-），男，汉族，山西祁县人，硕士，助理工程师，主要研究领域为飞行仿真与飞行控制。

华艺欣（1990-），男，汉族，陕西宝鸡人，硕士，工程师，主要研究领域为飞行力学与飞行控制。

*通讯作者：张 （1986-），男，汉族，陕西西安人，硕士，工程师，主要研究领域为飞行力学与飞行控制，飞行仿真。