非局域引力模型的能量条件及其限制
吴亚波, 张 雪, 赵月月, 陈博海, 张 楠, 柴云天
(1.辽宁师范大学 物理与电子技术学院, 辽宁 大连 116029;2.海军大连舰艇学院 基础部, 辽宁 大连 116018)
非局域引力模型的能量条件及其限制
吴亚波1, 张 雪1, 赵月月2, 陈博海1, 张 楠1, 柴云天1
(1.辽宁师范大学 物理与电子技术学院, 辽宁 大连 116029;2.海军大连舰艇学院 基础部, 辽宁 大连 116018)
深入探讨一种修正引力理论,即由马焦雷(M. Maggiore)和曼卡拉(M. Mancarella)提出的非局域引力模型,该理论模型是在爱因斯坦-希尔伯特作用量中加入了非局域修正项m2R□-2R.笔者详细研究并导出了该非局域引力理论满足的4种能量条件,即强能量条件,零能量条件,主能量条件和弱能量条件.为了揭示这些能量条件的物理意义,分别绘出了4种能量条件随引力模型参数α和宇宙红移z的演化图像.进一步,利用能量条件对模型参数α加以限制,给出了模型参数的取值范围.
爱因斯坦-希尔伯特作用量;非局域引力;能量条件
天文观测数据[1-3]表明宇宙目前正处在一个加速膨胀阶段,解释这个现象是现代宇宙学的一大难题.爱因斯坦场方程描述了时空几何与物质分布的内在关系.解释加速膨胀现象的理论方法一般分为修改爱因斯坦场方程的几何部分或物质部分.一方面,有理由相信驱动宇宙的加速膨胀可能是暗能量,它是一种具有负压强的额外组分且是当前宇宙总能量的主要成分.虽然多年来各国学者从理论上提出了众多暗能量模型,并对其进行了广泛研究[4-6].遗憾的是,暗能量的本质属性及其源问题始终困惑着人们,至今人们找不到任何已知粒子能够满足暗能量的性质.目前被广泛接受的暗能量模型是宇宙学常数Λ[7],即Λ冷暗物质(ΛCDM)模型.另一方面,修正引力理论作为暗能量的替代者也极具吸引力[8-10].在众多修正引力理论中,迪塞尔(S. Deser)和伍达德(R. P. Woodard)提出的非局域引力模型[11]是有竞争力的候选者之一,该模型的构建是在爱因斯坦-希尔伯特作用量中加入了非局域修正项f(□-1R).算符□-1是达朗贝尔算符□的逆,可以表示为延迟格林函数的卷积[12-13].这类模型最大的特点就是在辐射主导时期里奇标量R为零,直到物质主导时期后□-1R才开始以对数形式增长[14-15].该理论不需要引入暗能量就能再现目前宇宙的加速膨胀,既能避免精调问题和鬼极问题,又能实现宇宙从辐射主导到物质主导转换的延迟效应.同时,在低能极限下又能退化为爱因斯坦引力.然而该模型的不足之处是与大尺度结构观测数据不符.最近,马焦雷(M. Maggiore)和曼卡拉(M. Mancarella)提出一个新的非局域引力模型[16](下文简称为M-M非局域引力模型),该理论模型是在拉氏量中加入修正项m2□-2R,引入质量标度m,它的量纲为哈勃参数的今天值H0.非局域项是由单参数m控制,替代了ΛCDM宇宙模型中参数Λ,可以直接由观测检测,这个模型目前受到更多的关注[17-19].
能量条件[20]目前已广泛应用于各种修正引力理论,研究其对引力模型参数的限制[21-30].于是自然产生这样的问题:(1)在非局域引力框架下,能否导出M-M模型的4种能量条件:强能量条件(SEC),零能量条件(NEC),主能量条件 (DEC)和弱能量条件(WEC).(2)利用这些能量条件能否给出对M-M非局域引力模型的限制条件,即能否给出模型参数的取值范围.研究结果表明,不仅能导出该非局域引力模型的能量条件,而且利用SEC和NEC还能给出模型参数的限制范围.文中计算采用的度规号差为+2,并令光速c=1.
1 M-M非局域引力模型的场方程
考虑M-M非局域引力模型的作用量[16]
(1)
式中,质量标度m的量纲为哈勃参数的今天值H0,这里取m=αH0,α是常数,称它为模型参数.协变标量达朗贝尔算符定义为
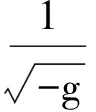
(2)
通常由延迟格林函数可求解出非局域项□-1R,它们具有关系式[13,17]:

(3)
这里,G(x,x′) 是算符□-1作用在标量上的格林函数.将作用量(1)对度规gμ ν作变分,得到非局域引力场方程

(4)
其中,
Kμ ν=2(Gμ ν-2μν)(□-2R)+2gμ ν(□-1R)-gμ ν(□-1R)2+
μ(□-2R)ν(□-1R)+ν(□-2R)μ(□-1R)-gμ νρ(□-2R)ρ(□-1R),
(5)
这里□=gμ νμν,物质的能量-动量张量Tμ ν为
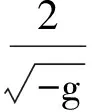
(6)
根据文献[16]的局域化处理方法,定义如下辅助标量场
U≡-□-1R,
(7)
S≡-□-1U=□-2R,
(8)
注意其初始条件都为0,于是修改的爱因斯坦场方程中的非局域项就改写为局域形式
Kμ ν=2(Gμ ν-μν)S-2gμ νU-gμ νU2-(μSνU+νSμU) -gμ νρSρU.
(9)
实际上,在对式(7)和式(8)进行数值积分的过程中,引入无量纲变量V=H0S和无量纲的哈勃参数h=H(t)/H0更为方便.于是,辅助标量场的运动方程可以表示为
U″+(3+ζ)U′=6(2+ζ),
(10)
V″+(3+ζ)V′=h-2U,
(11)
其中,ζ=h′/h,撇表示对时间坐标x=lna求导.根据方程(9),其时间分量为
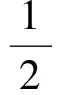
,
(12)
由此可得
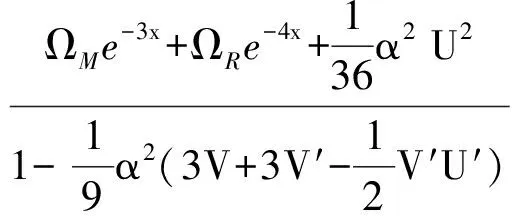
,
(13)
和

(14)
其中,ΩM和ΩR分别是物质和辐射的能量密度参数.方程(10)和方程(11)提供了一组关于标量场U和V的微分方程组,利用h2和ζ的表达式,方程组的解可以直接通过数值积分得到.
2 能量条件及其限制条件
考虑空间平坦的弗里德曼-罗伯森-沃克(FRW)宇宙背景,其时空度规为
ds2=-dt2+a2(t)dx2.
(15)
为讨论方便,将非局域引力场方程(4)改写为如下的有效引力场方程
(16)
其中,有效的能量-动量张量为

(17)
进一步,它的时间和空间分量分别对应有效能量密度和有效压强
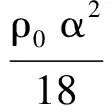
(18)
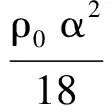
(19)
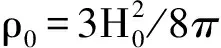
SEC:ρeff+3peff≥0⟹

(20)
NEC:ρeff+peff≥0⟹

(21)
DEC:ρeff-peff≥0⟹

(22)
WEC:ρeff≥0⟹

(23)
进一步,为了深入剖析能量条件的4个不等式,在图1和图2中笔者绘出了4个能量条件(即方程(20)~方程(23))随模型参数α和红移z的演化图像.取ΩM=0.308,ΩR=0.001和wR=1/3[3].从图1容易看出为了满足强能量条件(SEC)和零能量条件(NEC),模型参数的取值范围受到限制,分别为|α|≤0.26和|α|≤0.53.然而,从图2容易看出,无论模型参数α取何值,主能量条件(DEC)和弱能量条件(WEC)总被满足,由此说明它们对模型参数α的取值没有任何限制.

图1 左图:SEC (ρeff+3peff≥0)随模型参数α和红移z的演化;右图:NEC(ρeff+peff≥0)随模型参数α和红移z的演化Fig.1 Left panel:the evolution of SEC (ρeff+3peff≥0) with model parameter α and redshift z;Right panel:the evolution of NEC (ρeff+peff≥0) with model parameter α and redshift z
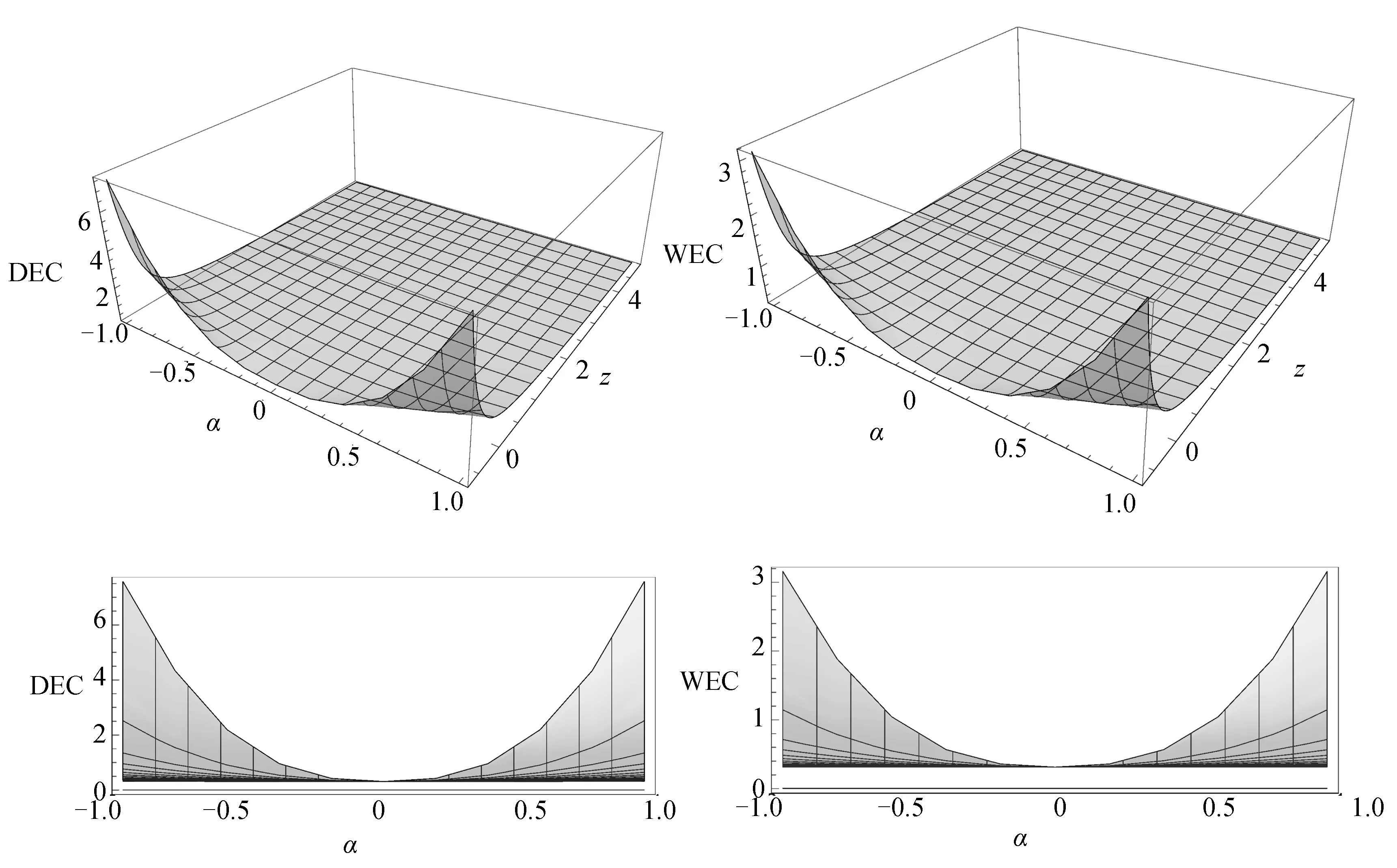
图2 左图:DEC(ρeff-peff≥0)随模型参数α和红移z的演化;右图:WEC(ρeff≥0)随模型参数α和红移z的演化Fig.2 Left panel:the evolution of DEC (ρeff-peff≥0) with model parameter α and redshift z;Right panel:the evolution of WEC (ρeff≥0) with model parameter α and redshift z
3 结 论
综上所述,笔者不仅导出了M-M非局域引力模型的4种能量条件(强能量条件,零能量条件,主能量条件和弱能量条件),而且通过作图分析了4种能量条件随模型参数α和红移z的演化规律以及对模型参数α的限制条件.研究结果表明,虽然主能量条件和弱能量条件对M-M非局域引力模型没有限制,即模型参数α可以任意取值,但强能量条件和零能量条件限制模型参数α的取值范围为|α|≤0.26.
[1] PERLMUTTER S,ALDERING G,GOLDHABER G,et al.Measurements ofΩandΛfrom 42 high redshift supernovae[J].The Astrophysical Journal,1999,517(2):565-586.
[2] RIESS A G,FILIPPENKO A V,CHALLIS P,et al.Observational evidence from supernovae for an accelerating universe and a cosmological constant[J].The Astrophysical Journal,1998,116(3):1009-1038.
[3] ADE P A R,AGHANIM N,ARNAUD M,et al.Planck 2015 results.Cosmological parameters[J].Astronomy and Astrophysics,2016,594(10):A13.
[4] COPELAND E J,SAMI M,TSUJIKAWA S.Dynamics of dark energy[J].International Journal of Modern Physics D,2006,15(11):1753-1936.
[5] LI M,LI X D,WANG S,et al.Dark Energy[J].Communications in Theoretical Physics,2011,56(3):525-604.
[6] CAI R G,GONG Y,WANG B.Some studies on dark energies[J].The Universe,2014,2(3):21-64.
[7] PEEBLES P J E,RATRA B.The cosmological constant and dark energy[J].Reviews of Modern Physics,2003,75(2):559-606.
[8] NOJIRI S,OGINTSOV S D.Unified cosmic history in modified gravity:fromF(R) theory to Lorentz non-invariant models[J].Physics Reports,2011,505(2/3/4):59-144.
[9] CLIFTON T,FERREIRA P G,PADILLA A,et al.Modified Gravity and Cosmology[J].Physics Reports,2012,513 (1/2/3):1-189.
[10] CAPOZZIELLO S,LAURENTIS M D.Extended theories of gravity[J].Physics Reports,2011,509(4/5):167-321.
[11] DESER S,WOODARD R P.Nonlocal cosmology[J].Physical Review Letters,2007,99(11):111301.
[12] KOSHELEV N A.Comments on scalar-tensor representation of nonlocally corrected gravity[J].Gravitation and Cosmology,2009,15(3):220-223.
[13] MAGGIORE M.Phantom dark energy from nonlocal infrared modifications of general relativity[J].Physical Review D,2014,89(4):043008.
[14] KOIVISTO T.Dynamics of nonlocal cosmology[J].Physical Review D,2008,77(12):123513.
[15] DEFFAYET C,WOODARD R P.Reconstructing the distortion function for nonlocal cosmology[J].Journal of Cosmology and Astroparticle Physics,2009(8):023.
[16] MAGGIORE M,MANCARELLA M.Nonlocal gravity and dark energy[J].Physical Review D,2014,90(2):023005.
[17] DIRIAN Y,MITSOU E.Stability analysis and future singularity of them2□-2Rmodel of non-local gravity[J].Journal of Cosmology and Astroparticle Physics,2014(10):065.
[18] DIRIAN Y,FOFFA S,KHOSRAVI N,et al.Cosmological perturbations and structure formation in nonlocal infrared modifications of general relativity[J].Journal of Cosmology and Astroparticle Physics,2014(6):033.
[19] BARREIRA A,LI B J,HELLWING W A,et al.Nonlinear structure formation in Nonlocal gravity[J].Journal of Cosmology and Astroparticle Physics,2014(9):031.
[20] HAWKING S W,ELLIS G F R.The Large scale structure of space-time[M].Cambridge:Cambridge University Press,1973:88-96.
[21] SANTOS J,ALCANIZ J S,REBOUCAS M J,et al.Energy conditions inf(R)-gravity[J].Physical Review D,2007,76(8):083513.
[22] BERTOLAMI O,SEQUEIRA M C.Energy conditions and stability inf(R) theories of gravity with non-minimal coupling to matter[J].Physical Review D,2009,79(10):104010.
[23] WANG J,WU Y B,GUO Y X,et al.Conditions and instability inf(R) gravity with non-minimal coupling between matter and geometry[J].The European Physical Journal C,2010,69(3):541-546.
[24] GARCIA N M,HARKO T,LOBO F S N,et al.Energy conditions in modified Gauss-Bonnet gravity[J].Physical Review D,2011,83(10):104032.
[25] LIU D,REBOUCAS M J.Energy conditions bounds onf(T) gravity[J].Physical Review D,2012,86(8):083515.
[26] ZHAO Y Y,WU Y B,LU J B,et al.Modifiedf(G) gravity models with curvature-matter coupling[J].The European Physical Journal C,2012,72(3):1924.
[27] SHARIF M,ZUBAIR M.Energy conditions inf(R,T,Rμ νTμ ν) gravity[J].Journal of High Energy Physics,2013(12):79.
[28] ATAZADEH K,DARABI F.Energy conditions inf(R,G) gravity[J].General Relativity and Gravitation,2014,46(1):1664.
[29] JAWAD A,RANI S.Non-minimal coupling of torsion-matter satisfying null energy condition for wormhole solutions[J].The European Physical Journal C,2016,76(12):704.
[30] SHARIF M,IKRAM A.Energy conditions inf(G,T) gravity[J].The European Physical Journal C,2016,76(11):640.
Energy conditions and constraints on the non-local gravity model
WUYabo1,ZHANGXue1,ZHAOYueyue2,CHENBohai1,ZHANGNan1,CHAIYuntian1
(1.School of Physics and Electronic Technology, Liaoning Normal University, Dalian 116029, China; 2.Department of Basic, Dalian Naval Academy, Dalian 116018, China)
In this paper,the authors explored a class of modified gravity model,namely,the so-called non-local gravity model proposed by M.Maggiore and M.Mancarella,which is obtained by adding a termm2R□-2Rto the Einstein-Hilbert action.The four energy conditions of the non-local gravity model,i.e.,the strong energy condition,the null energy condition,the dominant energy condition and the weak energy condition are studied and derived in detail.In order to get some insights on the meaning of the energy conditions,the evolutions of four energy conditions with the model parameterαand redshiftzare illustrated,and the constraints on the model parameterαare given by using these energy conditions.
Einstein-Hilbert action;non-local gravity;energy conditions
2017-03-17
国家自然科学基金资助项目(11175077;11575075;11547156);辽宁省自然科学基金资助项目(L20168366)
吴亚波(1961-),女,辽宁辽阳人,辽宁师范大学教授,博士,博士生导师.E-mail:ybwu61@163.com
1000-1735(2017)02-0167-06
10.11679/lsxblk2017020167
O411
A

