基于压缩感知中矩阵分解的观测矩阵改进

兰明然，王友国

(南京邮电大学 理学院，江苏 南京 210046)

基于压缩感知中矩阵分解的观测矩阵改进

兰明然，王友国

(南京邮电大学 理学院，江苏 南京 210046)

观测矩阵构造是压缩感知(CS)理论中的重点。在构造观测矩阵中，应尽可能地降低观测矩阵与稀疏变换基之间的相关性，同时增大观测矩阵列的独立性。为此，提出了一种新的改进方法。该方法采用梯度下降法处理Gram矩阵以降低其非对角线元素，在对所得到的观测矩阵进行QR分解的基础上，再对QR分解后的矩阵进行奇异值(SVD)分解，以进一步增大观测矩阵的列独立性。为了验证所提出算法的有效性，将所得观测矩阵分别与未优化的高斯矩阵、经SVD分解优化的高斯矩阵和梯度下降法优化的高斯矩阵在同等压缩比下进行了对比仿真实验。对比仿真实验结果表明，应用所提出算法而得到的矩阵具有较好的重构性能，特别当压缩比小于0.3时，对应于未经优化的观测矩阵，峰值信噪比提高约2至3倍。

压缩感知；观测矩阵；QR分解；SVD分解

0 引 言

传统的奈奎斯特采样定理要求信号采样频率不低于信号带宽的两倍，这样才可不失真地实现重构。近年来，Donoho等在信号分解以及逼近理论的基础上，提出一种全新的信号采样理论—压缩感知(Compressive Sensing,CS)[1-2]。该理论指出：利用信号的稀疏性(或可压缩性)先验条件，通过一定的线性或非线性的解码模型可以以高概率恢复原始信号[3]。其中测量矩阵的研究对信号重构精度有直接影响，其性能越好，信号恢复越好。因此，测量矩阵的构造至关重要。

CS理论研究表明，信号的精确重构要求观测矩阵满足RIP[4-5]，该性质同观测矩阵与稀疏基不相关[6]等价。文献[7]引用相关系数概念，其指观测矩阵与稀疏矩阵之间列向量内积的最大值。由已有的理论可知，若观测矩阵与稀疏矩阵的相关性特别小，测量值的数量就能逼近理论值，且能重构出信号的稀疏范围是比较大的[8]。目前，关于降低两者互相关性的研究有：赵瑞珍等[9]采用特征值分解法来减小相关系数，并研究了基于Gram矩阵的整体互相关系数的方法；Nhat V D M等提出一种有效投影法[10]，该方法提取稀疏变换基中奇异值向量的部分列向量，并用这些列向量组成观测矩阵，进而使得提取出的矩阵与稀疏矩阵间的非相关性增大；Elad等[11]为了减小非对角线上的元素，在阈值上进行一些处理，并提出以Gram阵为基础的t平均互相关的性质； Abolghasemin等[12]研究了梯度下降法在Gram矩阵中的影响与作用，并与特殊矩阵进行比较。

为此，将梯度下降法和矩阵分解相结合，对压缩感知矩阵进行优化，以降低观测矩阵与稀疏矩阵间的互相关性并增大观测矩阵列独立性，进一步优化后得到一个新矩阵，并将提出方法与未优化的高斯矩阵、SVD分解优化的高斯矩阵和梯度下降法优化的高斯矩阵在同等压缩比下的性能进行了对比分析。仿真结果表明，应用提出方法所获得的矩阵有较好的重构性能，特别是在压缩比较小时的优势更加明显。

1 压缩感知理论简介

压缩感知，是给定一个可稀疏或压缩的原始信号，通过某个特定的矩阵将其投影到一个低维空间，再利用一定的重构算法重构出原始信号[1]。具体如下：

(1)设x是一维离散信号，长度为N，可表示为x(n),n=1,2,…,N。根据信号稀疏分解理论，N维离散信号x=(x1,x2,…,xN)T可表示一组标准正交基的线性组合。

(1)

常见的稀疏基有DCT基、小波基及傅里叶基等等，文中采用小波基。

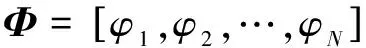
y=Φx

(2)

结合式(1)与式(2)得：

y=Φx=ΦΨs=Θs

(3)

其中，Φ和Θ=ΦΨ均是M×N矩阵，分别称为测量矩阵和感知矩阵。

2 观测矩阵优化构造

常用的测量矩阵包括：高斯随机测量矩阵、贝努利随机测量矩阵、部分正交测量矩阵、循环测量矩阵、托普利兹测量矩阵、稀疏随机测量矩阵。现有的这些测量矩阵对信号的重构精度都很高，但也有其自身固有的不足，如随机测量矩阵元素的不确定性及硬件难以实现性；确定性矩阵虽然稳定性较好，但测量数上却差强人意。针对这些缺点，提出了一种基于梯度下降法与矩阵分解结合的改进方法，进而得到性能优越的观测矩阵。

2.1 基于梯度下降法增大非相干性方法

(4)

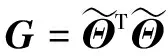
针对Gram矩阵的所有非对角线元素，利用梯度下降法让Gram矩阵逐渐逼近单位矩阵，以减小Gram矩阵非对角线元素。因单位矩阵中非对角线元素都为0，则相干系数为0，这是一种理想情况。可以优化Gram矩阵，使得它与单位矩阵很接近，即求解以下优化模型：

(5)

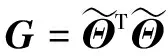
(6)

由上述分析可知，满足式(6)时测量矩阵与稀疏基间互相干系数最小。

定义误差函数：

(7)

根据文献[14]：

(8)

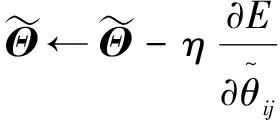
(9)

2.2 矩阵分解增大列独立性

由Donoho给出的测量矩阵特性[1]和矩阵分解理论可知，测量矩阵Φ的最小奇异值必须大于某一个非负常数η1。矩阵的最小奇异值与矩阵线性相关性具有紧密联系[15]，矩阵最小奇异值越大，其列相关性越弱，独立性越强。因此测量矩阵的最小奇异值对重构图像质量起着致关重要的作用。

2.2.1 矩阵QR分解

2.2.2 矩阵奇异值分解

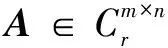
(10)

其中，Σ=diag(δ1,δ2,…,δr)，且δ1≥δ2≥…≥δr>0，δi(i=1,2,…,r)是A的正奇异值。式(10)称为矩阵A的奇异值分解。

定义2：任意复矩阵A∈Cm×n，若存在G∈Cn×m，满足四个Penrose方程(AGA=A；GAG=G；(AG)H=AG；(GA)H=GA)中的某几个或全部，则称G为A的一个广义逆矩阵。若满足全部四个方程的广义逆矩阵称为A的Moore-Penrose逆，记为A+。

引理1：若向量x1，x2分别满足Ax1=y1，Ax2=y2，令d1=‖x1-x2‖p/‖x1‖p，d2=‖y1-y2‖p/ ‖y1‖p，则有d1≤k(A)d2，其中k(A)=‖A‖p*‖A+‖p。

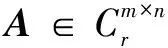
2.3 矩阵优化

根据以上分析，该优化方法思路是以高斯矩阵为初始观测矩阵，通过它构造Gram矩阵，利用梯度下降法对Gram矩阵逐步逼近于单位矩阵，通过迭代优化后的矩阵反向求出观测矩阵，且对得到的矩阵进行QR分解优化，并对分解后矩阵再进行SVD分解；继续用优化后的观测矩阵求解Gram矩阵，在不断进行Gram矩阵和观测矩阵反复作用的过程中，当迭代次数达到一定值时，输出此时的观测矩阵。通过上述优化后，观测矩阵不但与稀疏基间的互相关性减小，而且其列独立性得到增强。另外，由于每次迭代中QR分解优化时R只保存主对角线元素，观测矩阵保留着重要信息，同时通过均值算法修改奇异值得到的观测矩阵具有更好性能。新矩阵优化如下：

输入：稀疏矩阵Ψ，迭代步长η，最大迭代次数K。

初始化：Φ为一个任意的随机矩阵，Θ=ΦΨ。

循环：k=1:K。

对Θ做列单位化，Θ←Θ-ηΘ(ΘTΘ-I)，得到：Φ1←ΘΨ-1。

对Φ1进行近似QR分解优化：即先对Φ1进行QR分解，得到Φ1=QR，其中Q为正交阵，R为上三角矩阵；然后将R中的非对角线元素设置为零，得到R1；最后根据Φ2=QR1求得进一步更新的矩阵Φ2。

再根据Θ=Φ3Ψ，依次循环。

3 仿真结果与分析

为证实新矩阵优化算法相关理论的优越性，采用Matlab标准图像库中256*256的Lena图像进行仿真实验。对比算法的观测矩阵分别是初始高斯矩阵、经SVD分解优化的高斯矩阵[15]、梯度下降法优化的高斯矩阵[13]。在整个压缩感知过程中，原始矩阵采用高斯矩阵，稀疏基选取小波基，以OMP(正交匹配追踪)算法作为重构算法。在M/N<0.5时，新矩阵方法采用50次平均统计的结果为最后结果。4种观测矩阵在不同压缩比时的峰值信噪比见表1。

表1 不同压缩比下的PSNR

压缩比未优化/dB梯度下降法优化/dBSVD优化/dB所提优化/dB0．103．765．023．749．170．204．955．155．3214．900．3012．8318．9418．5827．120．4023．5425．6325．5929．300．5026．8228．2727．2831．51

由表1可知，梯度下降优化和SVD优化方法的峰值信噪比相差不大，而新矩阵优化方法相比其两种矩阵优化的峰值信噪比有显著提升，当压缩比为0.10、0.20、0.30、0.40、0.50时，Lena的PSNR比未优化方法的PSNR分别提高5.41 dB、9.95 dB、14.29 dB、5.76 dB和4.69 dB。通过比较可知，峰值信噪比的提高验证了新矩阵改进方法的可行性；而且当压缩比趋于0.30时，新矩阵优化的峰值信噪比提升最佳。图1为4种观测矩阵的峰值信噪比随压缩比变化趋势图。

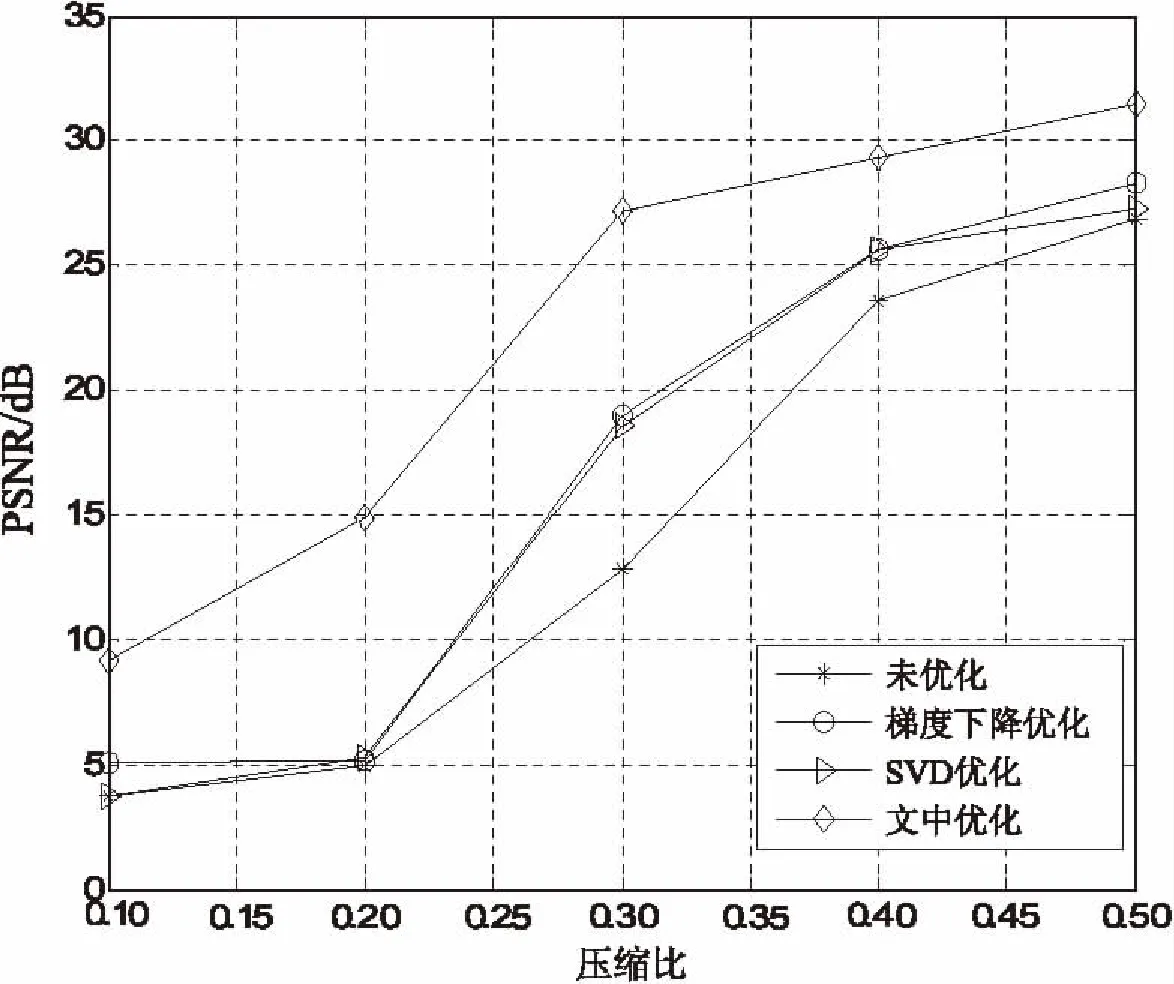
图1 观测矩阵的峰值信噪比随压缩比变化趋势图

从图1可看出，SVD优化和梯度下降优化效果很相近，其PSNR值比未优化的信噪比稍微增大；而新矩阵优化后的测量矩阵用于图像重构，所得PSNR值比SVD优化和梯度下降优化得到的PSNR值有显著提高，更优于未经优化的测量矩阵图像重构的效果。PSNR值的提高表明，新矩阵优化方法可提高重构精度，改善重构质量。图2给出了Lena和部分Lena在压缩比为0.5时4种算法的重构效果。

其中，图2(a)是未优化恢复的图像；图2(b)是梯度下降法优化恢复的图像；图2(c)是SVD优化恢复的图像；图2(d)是新矩阵优化恢复的图像。由对比可知，新矩阵优化方法重构图像质量优于SVD优化和梯度下降优化方法重建图像的质量；再则，图(a)和图(b)比较模糊，图(d)相对图(c)在下巴和嘴巴这些细节上重构效果更好，图(d)清晰度更接近原始图像。综上，提出算法在相同的压缩比下重构性能更高。

4 结束语

针对观测矩阵与稀疏变换基之间的相关性以及观测矩阵列的独立性,提出了一种基于梯度下降法的矩阵分解优化方法，得到了较优的观测矩阵。由仿真结果分析可知，提出的优化方法用于图像重构，在压缩比0.5时，重构图像的PSNR值比SVD优化和梯度下降优化的PSNR值提高约3.2 dB,优于未优化的PSNR值，尤其在压缩较少时，优势更明显。可见，提出的方法具有较好的适用性和较为显著的优越性能。

[1] Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[2] Candes E.Compressive sampling[C]//Proceeding of the international congress of mathematicians.[s.l.]:[s.n.],2006:1433-1452.

[3] 方 红,章权兵,韦 穗.基于非常稀疏随机投影的图像重建方法[J].计算机工程与应用,2007,43(22):25-27.

[4] Candes E, Tao T.Near optimal signal recovery form random projections:universal encoding strategies?[J].IEEE Transactions on Information Theory,2007,52(12):5406-5425.

[5] 马庆涛,唐加山.基于压缩感知的测量矩阵研究[J].微型机与应用,2013,32(8):64-67.

[6] Baraniuk R.A lecture on compressive sensing[J].IEEE Signal Processing Magazine,2007,24(4):118-121.

[7] Donoho D L,Stark P B.Uncertainty principles and signal recovery[J].SIAM Journal on Applied Mathematics,1989,49(3):906-931.

[8] 徐 静,王彩云.压缩感知测量矩阵优化混合方法[J].深圳大学学报:理工版,2014,31(1):58-62.

[9] Zhao Ruizhen,Qin Zhou,Hu Shaohai,et al.An optimization method for measurement matrix based on eigenvalue decomposition[J].Signal Processing,2012,28(5):654-656.

[10] Nhat V D M,Vo D,Halla S,et al.Efficient projection for compressed sensing[C]//Proceedings of the computer and information science.[s.l.]:[s.n.],2008:322-327.

[11] Elad M. Optimized projections for compressed sensing[J].IEEE Transactions on Signal Processing,2007,55(12):5695-5702.

[12] Abolghasemin V,Ferdowsi S,Makkiabadi B,et al.A robust approach for optimization of the measurement matrix in compressed sensing[C]//International workshop on cognitive information processing.Elba Island:IEEE Press,2010:388-392.

[13] Abolghasemin V,Ferdowsi S,Sanei S.A gradient-based alternating minimization approach for optimization of the measurement matrix in compressed sensing[J].Signal Processing,2012,92(3):999-1009.

[14] Abolghasemi V,Ferdowsi S,Makkiabadi B,et al.On optimization of the measurement matrix for compressive sensing[C]//18th European signal processing conference.[s.l.]:IEEE,2010:427-431.

[15] 彭玉楼,何怡刚,林 斌.基于奇异值分解的压缩感知噪声信号重构算法[J].仪器仪表学报,2012,33(12):2655-2660.

[16] 傅迎华.可压缩传感重构算法与近似QR分解[J].计算机应用,2008,28(9):2300-2302.

Improvement of Measurement Matrix with Matrix Decomposition in Compressive Sensing

LAN Ming-ran,WANG You-guo

(College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210046,China)

The structure of measurement matrix is the key point in the theory of Compressive Sensing (CS).In the measurement matrix constructing,it is possible to reduce the correlation between the measurement matrix and the sparse transformation matrix,and to increase the independence of the measurement matrix.A new improved method has been proposed for this purpose,which uses gradient Gram matrix to reduce its non-diagonal elements with descent method of measurement matrix obtained by QR decomposition.After decomposition of the QR matrix,Singular Value Decomposition (SVD) has been implemented to further increase the independence among the measurement matrix.In order to verify the effectiveness of the proposed algorithm,contrast experiments of matrix acquired by the proposed method with three types of Gauss matrices,such as these without optimization,optimized by SVD decomposition and optimized by gradient descent method,have been carried out at the same compression.The experimental simulation results show that the proposed algorithm and thus the reconstruction matrix have displayed better performance,especially when the compression ratio is less than 0.3,the peak signal-to-noise ratio has increased about 2 to 3 times comparing with the measurement matrix without optimization.

compressive sensing;measurement matrix;QR decomposition;singular value decomposition

2016-07-05

2016-11-04 网络出版时间：2017-04-28

国家自然科学基金资助项目(61179027)

兰明然(1992-)，女，硕士研究生，研究方向为信号处理理论与应用；王友国，教授，博士生导师，研究方向为信息理论及应用、编码理论及应用、随机共振理论与研究。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170428.1703.048.html

TP31

A

1673-629X(2017)06-0056-04

10.3969/j.issn.1673-629X.2017.06.012