基于随机场的岩石边坡三维稳定性分析

牛燚炜+周小平+钱七虎

摘要：基于随机场理论，考虑了岩石材料属性的空间变异性对岩石边坡稳定性的影响，将边坡主滑面上的摩擦系数和粘聚力视为高斯随机变量，确定了主滑面上的摩擦系数和粘聚力的均值、方差和协方差，获得了两个随机量之间的相关系数和互相关长度。在此基础上，对岩石边坡进行了三维稳定性分析，确定了岩石边坡的稳定系数和失效概率。数值计算结果表明，摩擦系数和粘聚力的空间变异性对边坡稳定性有重要影响。

关键词：岩石边坡；稳定系数；失效概率；随机场

中图分类号：TU475文献标志码：A文章编号：16744764（2017）03012909

Abstract：The stability of rock slopes is analyzed by considering the spatial variability of the rock materials based on theory of random fields. Both the cohesion and frictional coef cient along the main sliding surface are treated as Gaussian random elds， and the mean value， variance， covariance of the cohesion and frictional coef cient are determined. Spatial correlation lengths and the crosscorrelation between cohesion and coef cient are obtained. Threedimensional stability assessment of rock slopes is analyzed to obtain the factor of safety and probability of failure of rock slope. The numerical results show that the spatial variability of cohesion and coef cient of friction significantly affect the safety of rock slopes.

Keywords：rock slopes； factor of safety； probability of failure； random fields

边坡失稳已与地震、火山爆发并列成为世界三大地质灾害（或地质灾害源）[1]。当边坡岩体内发育有层间软弱夹层或较大的断层、节理和裂隙时，则容易发生滑动破坏。在边坡稳定性分析过程中，需要考虑岩土工程是土木工程中最受不确定性主导的分支学科，因为它通常与高度变化的天然材料密切相关。岩性参数误差有3个主要来源，即材料固有变异性、统计误差、系统误差[2]。固有变异性是指即使在各向同性岩石介质中，岩石性质表现出变异性。由于现场采样和实验室数据的有限性，岩石属性的统计数据（例如均值和标准差）受（统计的）不确定性的影响，但是这类不确定性会随样品数量的增加而减少。系统不确定性是由于实验室和原位条件存在不同因素，如实验规模、各向异性和水饱和度等[3]。笔者重点研究材料的固有变异性（其在均质材料中也会比较大）及其对失效概率的影响。

传统边坡稳定性的评价方法主要有刚体极限平衡法、赤平投影法、有限元法以及模拟试验等。为了避免材料的不确定性所造成的影响，这些方法对于设计参数、稳定系数等一般都采用偏保守的值进行设计。为了考虑参数的变异性和不确定性，在传统方法基础上引入随机场理论十分必要。一般情况下，得出随机变量的分布函数可以说是一个相当复杂的问题，并且找到精确解也有相当困难。祁小辉等[4]采用谱表现法建立了表征土体空间变异性的随机场模型，提出了考虑土体空间变异性的边坡最危险滑动面随机分析方法。蒋水华等[5]提出了基于多重响应面与子集模拟的边坡可靠度分析方法。舒苏荀等[6]提出一种能合理考虑土性参数空间变异性的边坡模糊随机可靠度分析方法。Einstein等[7]在岩石边坡中采用了蒙特卡罗方法计算。唐小松等[8]研究了表征抗剪强度参数间相关性的Copula函数对边坡可靠度的影响，提出了无限边坡失效概率计算的直接积分方法。Pantelidis等[9]和Griffiths等[10]等分別用一维跟二维随机变量考虑岩石空间变异性对边坡稳定性的影响。Gravanis等[11]研究了岩石材料属性的空间变异性对岩石边坡失效概率的影响。然而，Gravanis仅仅研究了重力作用下岩石边坡的二维稳定性问题。但是实际边坡或滑坡体是三维问题，将三维问题简化为二维问题，会带来计算结果的较大误差。为了合理地评价岩石边坡的稳定性，笔者将Gravanis的二维随机场方法延伸为三维随机场方法，并把底面摩擦系数和粘聚力视为高斯随机变量，分析岩石边坡的三维稳定性问题。

1基于随机场理论的岩石边坡三维稳

定性分析1.1高斯随机场的几个假定

为简化计算模型，做如下假设：

1）高斯过程：联合概率分布函数为多元正态随机分布过程，其巨大的优势是只需均值向量和协方差矩阵就可以确定其完整分布函数。

2）平稳性或统计均匀性：联合概率分布函数的空间非独立性，即它依赖于点的相对位置关系。这个假设意味着均值、协方差和高阶矩是常量，且联合概率分布函数也是恒定的，不随时间和空间变化。

3）各向同性：在二维或更高维度的随机场中，各向同性是指旋转不变形。在各向同性中，两个点的相关性仅跟两点之间距离有关，而与方向角度无关。

在上述假设下，只需知道3个数值即可求解：随机场的均值μ、随机场的方差σ2、随机场的空间变异程度。其中，随机场的空间变异程度由随机场的联合分布二阶矩表征，可以从协方差函数中获得[12]。

1.2边坡稳定极限平衡分析方法

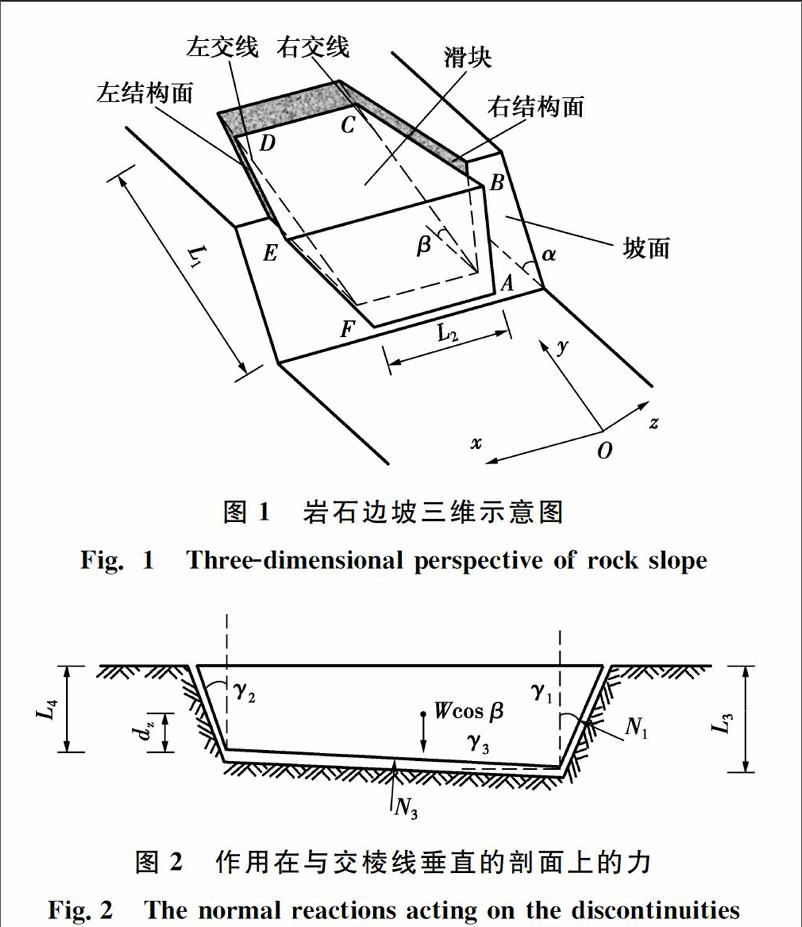
假定岩石边坡的可能滑动面如图1所示。为了简化计算，忽略孔隙水压力和基础荷载的作用，将上部岩体视为整体。边坡三维示意图如图1所示，作用在与交棱线垂直的剖面图如图2。

2应用实例

2.1当边坡体沿三面滑动时（γ3=0°），摩擦系数对边坡稳定性的影响

随机场变量为tan φ（x，y），其均值和方差分别为μ和σ。此时，粘聚力为常量。如图4和图5所示，z轴坐标为pf，x和y轴坐标分别为L1/θ1和L2/θ2。計算参数为：β=30°、γ1=0°、γ2=0°、γ3=0°、c3=40kPa、c1=40 kPa、c2=40 kPa、L1=10 m、L2=20 m、L3=1.5 m、ex=0.5 m、ey=1 m、W=1.8×105 kN。

如图4和图5所示，当tan φ（x，y）的相关长度θ1和θ2分别远远大于滑面的长L1和宽L2时，即（L1/θ1，L2/θ2）的值趋于0。如式（16）所示，方差s2tanφ的值趋于σ2tanφ。失效概率对于不同的摩擦系数均值趋于相应的定值。当相关长度θ1和θ2变小时，失效概率在稳定系数大于1时趋于0，在稳定系数小于1时趋于1。从图4和图5右半部分可知：当方差越大时，失效概率的值偏差越大；从图3和图4左半部分可知：当方差越大时，失效概率的值越向0.5靠近。图4和图5与Griffths等[15]的计算结果吻合。

2.2当边坡体沿三面滑动时（γ3=0°），摩擦系数和粘聚力对边坡稳定性的影响

如式（39）、（19）、（40）和（41）所示，失效概率pf与6个未知数（L1/θ1，L2/θ2）、（L1/θ1c，L2/θ2c）、（L1/θ1，c-tanφ，L2/θ2，c-tanφ）相关。在一张三维立体图中表示失效概率与6个未知量的关系比较困难。假设：（L1/θ1=L2/θ2）、（L1/θ1c=L2/θ2c），并取L1/θ1，L2/θ2c作为2个变量，此时θ1，c-tanφ和θ2，c-tanφ取极大值，γ1（L1/θ1，c-tanφ，L2/θ2，c-tanφ）取极值为1。其他计算参数为：μtanφ=tan26.25°和μtanφ=tan30.75°、σtanφ=tan5°、μc=40 kPa、σc=20 kPa、ρc-tanφ=0.2。

如图6所示，当摩擦系数和粘聚力的相关长度远小于滑面的长L1和宽L2时，则L1/θ1和L2/θ2c的值相应很大。从图6右半部分可知：失效概率pf的值在稳定系数F大于1时趋于0，在稳定系数F小于1时趋于1；当摩擦系数和粘聚力的相关长度远大于滑面的长L1和宽L2时，则L1/θ1和L2/θ2c的值相应很小。从图6左半部分可知：失效概率的值趋于定值。

2.3给定失效概率下的边坡稳定系数

对于给定的失效概率，稳定系数的值与相关长度有关。当σtanφ=tan5°时，pfmax分别取10%、1%、0.1%，稳定系数与相关长度（L1/θ1，L2/θ2）的关系如图7所示。当（L1/θ1，L2/θ2）较小时，对不同失效概率，稳定系数对应于相应的定值，且该值随失效概率的减小而增加；当（L1/θ1，L2/θ2）较大时，对不同失效概率，稳定系数趋于1。

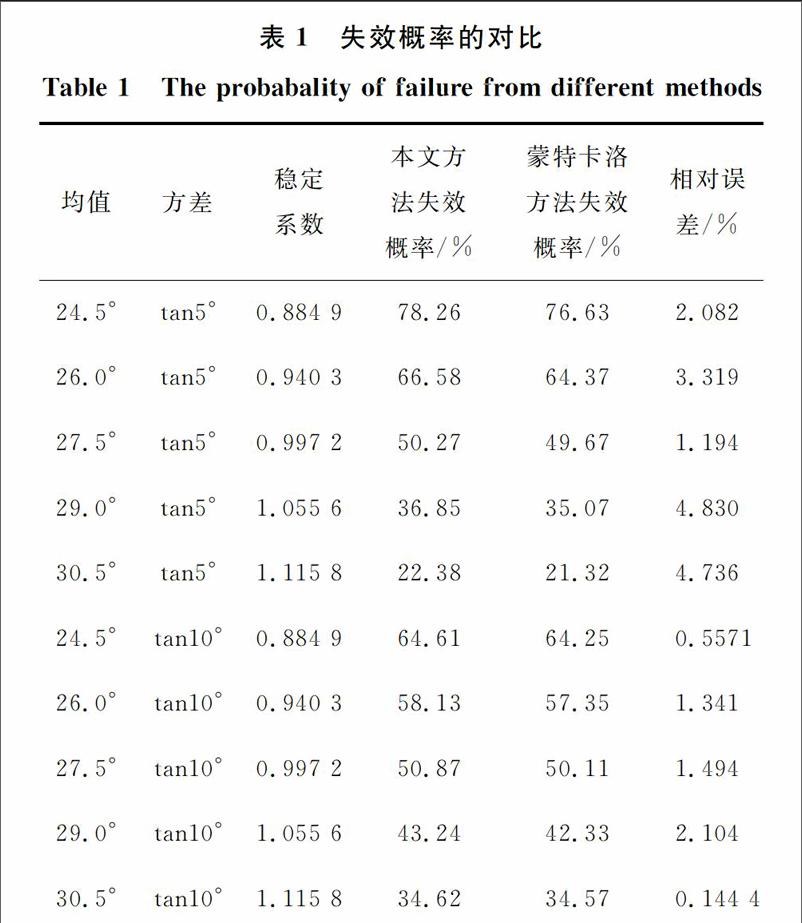
2.4不同方法下边坡失效概率对比

表1中列出了采用蒙特卡洛方法[16]计算的失效概率。表1中均值为滑动面摩擦角的平均值。从表1可知，该方法的计算结果与蒙特卡洛方法的计算结果吻合，最大误差为4.83%，证明了该方法的有效性。需要指出的是：本文的计算条件为相关长度（L1/θ1，L2/θ2）趋近于（0，0），由式可知s2tanφ等于σ2tanφ。

3结论

在岩质或土质边坡中，滑面材料的空间变异性对边坡的稳定具有重要的影响。采用随机场理论对岩质边坡进行了三维稳定性分析，建立了边坡失效概率与相关长度之间的关系。算例表明，相关长度对边坡失效概率具有重要的影响，不同的相关长度，导致不同的失效概率。同时，该方法可以退化为二维问题，其结果和Gravanis的方法一致。随机场理论的结果，与蒙特卡洛方法计算的结果吻合，验证了方法的有效性。

参考文献：

[1] 张永兴.边坡工程学[M]. 北京：中国建筑工业出版社，2008.

ZHANG Y X. Slope engineering [M]. Beijing： China Architecture & Building Press， 2008. （in Chinese）

[2] GRAVANIS E， PANTELIDIS L， GRIFFITHS D V. An analytical solution in probabilistic rock slope stability assessment based on random fields [J]. International Journal of Rock Mechanics & Mining Sciences， 2014， 71： 1924.

[3] DUZGUN H S B， YUCEMEN M S， KARPUZ C. A probabilistic model for the assessment of uncertainties in the shear strength of rock discontinuities [J]. International Journal of Rock Mechanics & Mining Sciences， 2002， 39（6）： 74354.

[4] 祁小辉， 李典庆， 周创兵，等. 考虑土体空间变异性的边坡最危险滑动面随机分析方法[J]. 岩土工程学报， 2013， 44（4）：745753.

QI X H， LI D Q， ZHOU C B， et al. Stochastic analysis method of critical slip surfaces in soil slopes considering spatial variability [J]. Chinese Journal of Geotechnical Engineering， 2013， 44（4）： 745753. （in Chinese）

[5] 蒋水华， 魏博文， 姚池，等. 考虑概率分布影响的低概率水平边坡可靠度分析[J]. 岩土工程学报， 2016， 38（6）：10711080.

JIANG S H， WEI B W， YAO C， et al. Reliability analysis of soil slopes at lowprobability levels considering effect of probability distributions [J]. Chinese Journal of Geotechnical Engineering， 2016， 38（6）： 10711080. （in Chinese）

[6] 舒苏荀， 龚文惠， 王佳，等. 各向异性随机场下的边坡模糊随机可靠度分析[J]. 岩土工程学报， 2015， 37（7）：12041210.

SHU S X， GONG W H， WANG J， et al. Fuzzyrandom reliability analysis of slope stability in anisotropic random fields [J]. Chinese Journal of Geotechnical Engineering， 2015， 37（7）： 12041210. （in Chinese）

[7] EINSTEIN H H， VENEZIANO D， BAECHER G B， et al. The effect of discontinuity persistence on rock slope stability [J]. International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts， 1983， 20（5）： 227236.

[8] 唐小松，李典庆，周创兵，等.基于Copula函数的抗剪强度参数间相关性模拟及边坡可靠度分析[J].岩土工程学报， 2012， 34（12）： 22842291.

TANG X S， LI D Q， ZHOU C B， et al. Modeling dependence between shear strength parameters using Copulas and its effect on slope reliability [J]. Chinese Journal of Geotechnical Engineering， 2012， 34（12）： 22842291. （in Chinese）

[9] PANTELIDIS L， GRAVANIS E， GRIFFITHS D V. Influence of spatial variability on rock slope reliability using 1D random fields [M]// Engineering Geology for Society and Territory Volume 2. Springer International Publishing， 2015： 12351238.

[10] GRIFFITHS D V， HUANG J S， FENTON G A. Influence of spatial variability on slope reliability using 2D random fields [J]. Journal of Geotechnical & Geoenvironmental Engineering， 2009， 135（10）： 13671378.

[11] GRAVANIS E， PANTELIDIS L， GRIFFITHS D V. An analytical solution in probabilistic rock slope stability assessment based on random fields [J]. International Journal of Rock Mechanics & Mining Sciences， 2014， 71： 1924.

[12] FENTON G A， GRIFFITHS D V. Risk assessment in geotechnical engineering [M]. Hoboken， NJ： Wiley， 2008.

[13] FENTON G A， VANMARCKE E H. Simulation of random fields via local average subdivision [J]. Journal of Engineering Mechanics， 1990， 116（8）： 17331749.

[14] 盛骤，谢式千，潘承毅.概率论与数理统计[M].北京：高等教育出版社，2008.

SHENG Z， XIE S Q， PAN C Y. Probability theory and mathematical statistics [M]. Beijing： Higher Education Press， 2008. （in Chinese）

[15] GRIFFITHS D V， FENTON G A. Probabilistic slope stability analysis by finite elements[J].Journal of Geotechnical & Geoenvironmental Engineering， 2004， 130：507518.

[16] 金畅. 蒙特卡洛方法中随机数发生器和随机抽样方法的研究[D]. 辽宁 大連：大连理工大学， 2005.

JIN C. Study on random number generator and random sampling in monte carlo method [D]. Dalian： Dalian University of Technology， 2005. （in Chinese）

（编辑胡英奎）