圆钢管混凝土轴压长柱极限承载力的稳定系数法
臧兴震+何子奇+徐创泽

摘要:为完善圆钢管混凝土轴压长柱极限承载力的计算理论,对比分析了中国国家标准GB 50936 — 2014和CECS 28: 2012中轴压短柱极限承载力的N0计算公式,并把GB 50936 — 2014中基于套箍系数的N0计算公式改写成统一的形式,提出了基于正则长细比的轴压长柱的稳定系数计算式,并通过36个试件的对比,对计算式的精度和适用范围进行了分析。研究表明,现行国标GB 50936—2014中基于套箍系数的N0计算公式更为精确,基于N0计算公式和本文的稳定系数,可以计算得到更为精确的轴压长柱的极限承载力。
关键词:钢管混凝土;轴压构件;极限承载力;稳定系数法;
中图分类号:TU311文献标志码:A文章编号:16744764(2017)03007508
Abstract:The ultimate strength formula of short columns under axial compression, which were given by the current code GB 509362014 and the current specification CECS 28: 2012, were compared and analyzed to improve the theory of ultimate strength of long concretefilled steel tubular columns under axial compression. The formula of the ultimate strength of short columns, basing on confinement coefficient which was given by GB 509362014, was rewritten as a unified form. A new stability coefficient was proposed for long concretefilled steel tubular columns under axial compression. The accuracy of the proposed stability coefficient was validated by 36 specimens. The results show that the formula of short columns based on the confinement coefficient and the proposed stability coefficient can provide good prediction of ultimate strength for both short and long concretefilled steel tubular columns under axial compression.
Keywords:concretefilled steel tubular columns;axial compression member;ultimate strength;stability coefficient method
钢管混凝土轴压构件由钢管和其核心混凝土两种材料组成。其中,核心混凝土受钢管的约束作用而强度提高,混凝土则延缓或阻止了钢管的面外局部屈曲[13]。钢管混凝土构件因其具有良好的承载性能和经济性能而广泛应用,关于钢管混凝土构件的研究也在轴压短柱[46]、轴压长柱[79]、偏压长柱[1013]、柱的抗震性能[1415]等方面不断深化,Min等[16]提出的钢管混凝土统一理论则把钢管和混凝土认为是一种材料,此外,双剪强度理论也分别应用于钢管混凝土的轴压短柱[17]、轴压长柱[18]的极限承载力研究。
经过学者们多年的不懈努力,现行中国国家标准《钢管混凝土结构技术规范》(GB 50936—2014)[19]于2014年12月1日开始实施,使得中国钢管混凝土结构的工程实践具有了国家标准。与此前的《钢管混凝土结构技术规程》(CECS 28: 2012)[20]相比,GB 50936—2014中钢管混凝土轴压长柱的极限承载力计算公式有了较大的改变:一是GB 50936—2014同时提供了基于构件正则长细比的轴心受压构件稳定系数φ和考虑长细比影响的承载力折减系数φl,二是GB 50936—2014中考虑长细比影响的承载力折减系数φl与CECS 28: 2012中的不同。
为了对准确合理应用现行国家标准GB 50936—2014指导中国钢管混凝土结构的工程实践,本文在分析该标准中轴压短柱极限承载力的基础上,提出了轴压长柱极限承载力计算的稳定系数法,并通过试验数值进行对比对其计算精度和适用范围进行验证。
1轴压短柱极限承载力的公式分析
1.1轴压短柱承载力的现行公式
现行国家标准《钢管混凝土结构技术规范》(GB 50936—2014)[19]给出了两种计算軸压短柱极限承载力的方法,一是基于钢管和混凝土作为一种材料的设计方法,记为GB 50936—2014的方法(Ⅰ),另一种则是基于极限平衡理论的设计方法,记为GB 50936—2014的方法(Ⅱ)。GB 50936—2014的方法(Ⅰ)和GB 50936—2014的方法(Ⅱ)对于钢管混凝土轴压短柱极限承载力的计算有较大区别。
中国协会标准CECS 28: 2012中轴压短柱极限承载力的计算方法与GB 50936—2014的方法(Ⅱ)相似,但后者由于考虑了不同强度等级混凝土对极限荷载的影响,更为细致。
为对比以上3种轴压短柱极限承载力的计算方法的不同,选取文献[4]中的56个外径为D、壁厚为t、几何长度为L的轴压短柱(图1),分别按照GB 50936—2014的方法 (Ⅰ)、GB 50936—2014的方法(Ⅱ)以及CECS 28: 2012中轴压短柱极限承载力的公式计算得到承载力N01、N02和N03,计算中对文献[4]中的单位采用1 kgf/cm2=1 MPa/9.81= (1 N/mm2)/9.81和1 kgf = 9.81 N进行了转换(表1)。
由表1可以看出,N0/Nu,exp的较大值以CECS 28: 2012的方法居多,最大值可达1.496;N0/Nu,exp的较小值以GB 50936—2014的方法(Ⅰ)居多,最小值为0.301;而由GB 50936—2014的方法(Ⅱ)得到的N0/Nu,exp的值最大值和最小值分别为1.120和0.541,大部分的N0/Nu,exp值与1比较接近。
1.2轴压短柱极限承载力的参数分析
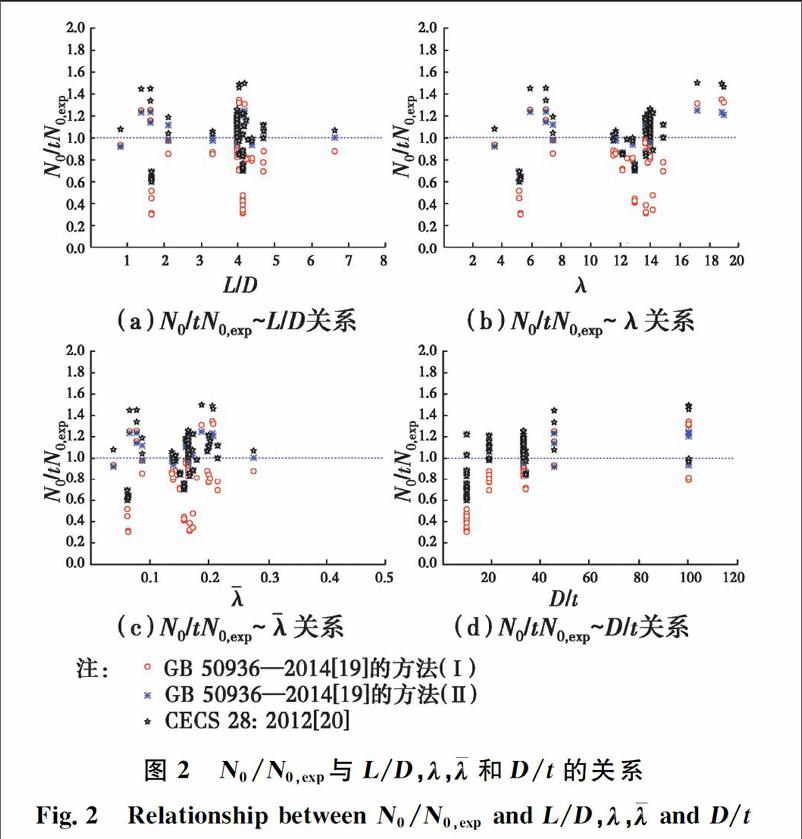
为确定不同参数对轴压短柱极限承载力的影响,图2分别给出了表1中的N0/Nu,exp值与L/D、λ、和D/t的关系,其中L为构件几何尺寸,D和t分别为构件的外径和壁厚,λ和分别为构件的长细比和正则长细比,λ和的定义见后文。由图2(a) ~ (c)可知,N0/Nu,exp的数值不随L/D、λ以及的增大呈规律性变化,这是因为对于轴压钢管混凝土短柱,由于L/D的数值被限制在较小的范围内(如L/D ≤ 4),构件是以全截面屈服为破坏模式的,故L/D、λ以及不是影响N0/N0,exp數值的关键因素。由图2(d)可看出,N0/N0,exp的较小值主要出现在径厚比D/t较小的试件上,即当径厚比D/t在10左右时GB 50936—2014 和CECS 28: 2012中的轴压短柱极限承载力计算公式均偏过于安全,这是因为径厚比D/t越小,钢管对核心混凝土的约束就越强,构件的实际承载力就越高。事实上,径厚比D/t在10左右的情况在实际工程中极少。
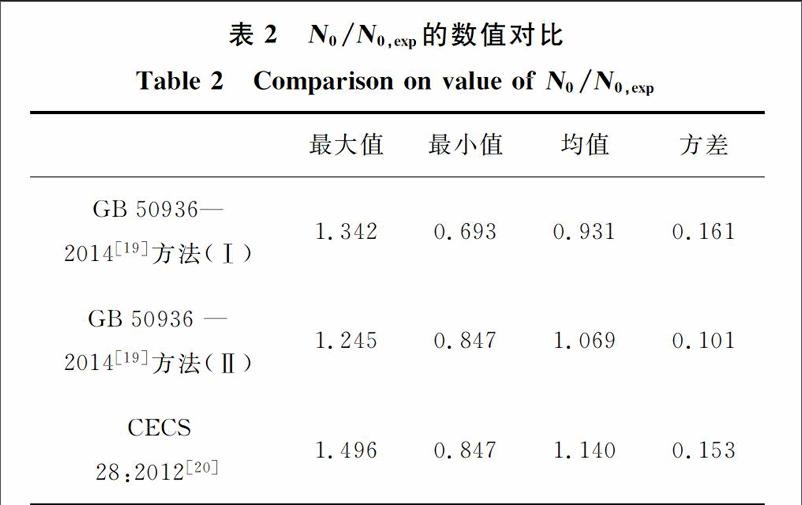
剔除表1中与径厚比D/t在10左右对应的N0/N0,exp值,可得表2所示的N0/N0,exp最大值、最小值、均值和方差。由表2可以看出,当径厚比D/t较大时,由GB 50936 — 2014的方法(Ⅱ)得到的N0/N0,exp的均值是三者之中与1.000最为接近,而最大值和方差是三者之中最小的。因此,建立轴压长柱极限承载力的稳定系数法时,以GB 50936 — 2014的方法(Ⅱ)的方法计算轴压短柱的极限承载力N0。
2轴压长柱极限承载力的稳定系数法
3本文稳定系数法计算式的验证
为验证本文计算式的精度,分别采用GB 50936—2014方法(Ⅰ)、GB 50936—2014方法(Ⅱ)、CECS 28: 2012和本文的稳定系数计算文献[7]中的26个轴压试件和文献[10]中的10个轴压试件的极限承载力,计算中轴压短柱极限承载力N0分别选用对应的计算式,本文的N0则选用式(2)和式(3)计算,计算结果分别为Nu1、Nu2、Nu3和Nu4(表3)。计算中采用1 kgf/cm2=1 MPa/9.81= (1 N/mm2)/981和1 kgf = 9.81 N把文献[7]和文献[10]的非国标单位转换为国标单位。如文献[7]中的fck = 347 kgf/cm2 =35.4 N/mm2, fa = 3 458 kgf/cm2 = 352.9 N/mm2,Ea = 2.05×106 kgf/cm2 = 209 184 N/mm2。对于混凝土弹性模量,则根据转换后的fck数值先查《混凝土结构设计规范》(GB 50010—2010)[21]确定出混凝土强度等级,再由该标准确定其弹性模量,如文献[7]中的fck=35.4 N/mm2与C55混凝土的fck =35.5 N/mm2几乎一致,则查GB 50010—2010可知其弹性模量为Ec = 3.55×104N/mm2。
表3还列出了文献[7]和文献[10]中的试验值Nu,exp以及比值Nu1/Nu,exp、Nu2/Nu,exp、Nu3/Nu,exp和Nu4/Nu,exp。由表3可知,在Nu1/Nu,exp、Nu2/Nu,exp、Nu3/Nu,exp和Nu4/Nu,exp中,Nu1/Nu,exp的最大值是四者之中最大的而最小值是四者之中最小的,尽管其平均值0.956较其他的平均值小,但其方差0.266表明GB 50936—2014方法(Ⅰ)的计算离散性较大。由表3可知,Nu4/Nu,exp值的最大值最小而最小值最大,其平均值和方差均较Nu2/Nu,exp和Nu3/Nu,exp的平均值和方差为小。因此,由GB 50936—2014的方法(Ⅱ)的N0计算式和本文的稳定系数可以计算得到更为准确的轴压长柱的极限承载力。
事实上,GB 50936—2014方法(Ⅱ)中轴压长柱极限承载力的计算公式是由CECS 28: 2012中的公式改进而得到的。图4对比了GB 50936—2014[19]与CECS 28: 2012[20]基于Le/D的稳定系数的计算式文献[7]中的试验数据。由图4可知,在4 ≤ Le/D ≤ 30范围内,由GB 50936—2014的方法(Ⅱ)的稳定系数计算式得到的更偏安全一些。此外,本文前述分析已指出GB 50936—2014的方法(Ⅱ)的N0公式也较CECS 28: 2012中的N0公式更能预测轴压短柱的极限承载力。因此,GB 50936—2014方法(Ⅱ)也比CECS 28: 2012更能准确计算轴压长柱的极限承载力。基于以上分析可知,本文的稳定系数在计算精度上较GB 50936—2014[19]的方法好。此外,本文的稳定系数具有明确的物理意义,而且,与国际主流标准的稳定系数制定方法一致,因此,本文的稳定系数计算方法可以作为一种有益的补充,指导钢管混凝土结构轴压长柱的稳定设计。
4结论
对比了轴心受压短柱极限承载力的计算式,提出了轴心受压长柱稳定承载力的计算式,并经36个试件进行验证。得到结论如下:
1)当径厚比D/t在10左右时,GB 50936—2014 和CECS 28: 2012中的轴压短柱极限承载力计算公式均偏过于安全。
2)GB 50936—2014中基于套箍系数的轴压短柱极限承载力的公式具有较高的精度。
3)本文的轴压长柱稳定系数具有明确的物理意义。由本文的稳定系数和GB 50936—2014中基于套箍系数的轴压短柱极限承载力公式,可以得到更为精确的轴压长柱极限承载力。
参考文献:
[1] GUO S C, LIU H F. Elastic analysis on postlocal bucklingof steel plates in thinwalled rectangular concretefilled steel tube columns [J]. Applied Mechanics & Materials, 2012, 204208:912916.
[2] BUKOVSK P, KARMAZNOV M, NEUBAUEROV P, et al. Buckling resistance of steel tubular columns filled by highstrength concrete [J]. International Journal of Mechanics, 2012,95:172177.
[3] DING F X, LU D R, BAI Y, et al. Comparative study of square stirrupconfined concretefilled steel tubular stub columns under axial loading [J]. ThinWalled Structures, 2016, 98:443453.
[4] 蔡绍怀,焦占拴. 钢管混凝土短柱的基本性能和强度计算 [J]. 建筑结构学报, 1984, 5(6): 1329.
CAI S H,JIAO Z S. Behavior and ultimate strength of short concretefilled steel tubular columns [J]. Journal of Building Structures, 1984, 5(6): 1329. (in Chinese)
[5] RUI X, LU Z, REN Z, et al. Experimental research on the performance of microexpansion and selfcompacting concretefilled steel tubular short column under axial compression [J]. Procedia Earth & Planetary Science, 2012, 5(32):1924.
[6] DING F X, FANG C, BAI Y, et al. Mechanical performance of stirrupconfined concretefilled steel tubular stub columns under axial loading [J]. Journal of Constructional Steel Research, 2014, 98:146157.
[7] 蔡绍怀,顾万黎. 钢管混凝土长柱的性能和强度计算 [J].建筑结构学报, 1985, 6(1): 3240.
CAI S H,GU W L. Behaviour and ultimate strength of long concretefilled steel tubular columns [J]. Journal of Building Structures, 1985, 6(1): 3240. (in Chinese)
[8] QI H T, GUO L H, LIU L P, et al. Axial load behavior and strength of tubed steel reinforcedconcrete (SRC) stub columns [J]. ThinWalled Structures,2011,49 (9):114150.
[9] ZHANG J C, YANG J. Study on mechanism of Lshaped concretefilled steel tubular columns subjected to axial compression [J]. Advanced Materials Research, 2012, 476/477/478:24632468.
[10] 蔡紹怀,邸小坛. 钢管混凝土偏压柱的性能和强度计算[J]. 建筑结构学报, 1985, 6(4): 3242.
CAI S H,DI X T. Behaviour and ultimate strength of concretefined steel tubular columns under eccentric loading [J]. Journal of Building Structures, 1985, 6(4): 3242. (in Chinese)
[11] ZHOU X H, YAN B, LIU J P. Behavior of square tubed steel reinforcedconcrete (SRC) columns under eccentric compression [J]. ThinWalled Structures, 2015, 91:129138.
[12] ZHOU X H, LIU J P, WANG X, et al. Behavior and design of slender circular tubedreinforcedconcrete columns subjected to eccentric compression [J]. Engineering Structures, 2016, 124:1728.
[13] ABDELGADIR E, BOHAI J, ZHONGQIU F, et al. The behavior of lightweight aggregate concrete filled steel tube columns under eccentric loading [J]. Steel & Composite Structures, 2011, 11(6):469488.
[14] HAN L H, LI W. Seismic performance of concretefilled steel tubular (CFST) structures [C]// Seismic Design of Industrial Facilities,2014.
[15] LIU J, ABDULLAH J A, ZHANG S. Hysteretic behavior and design of square tubed reinforced and steel reinforced concrete (STRC and/or STSRC) short columns [J]. ThinWalled Structures, 2011, 49(7):874888.
[16] MIN Y U, ZHA X, JIANQIAO Y E, et al. A unified formulation for circle and polygon concretefilled steel tube columns under axial compression [J]. Engineering Structures, 2013, 49(2):110.
[17] WANG J, ZHAO J H, SAI W U, et al. Calculation of axial bearing capacity of rectangular concretefilled steel tube short column based on twin shear unified strength theory [J]. Journal of Architecture & Civil Engineering, 2011,28(3):8892.
[18] ZHANG Y, ZHAO J. Calculation of compressive bearing capacity of concretefilled twin steel tubes based on twin shear unified strength theory [J]. Mechanics in Engineering, 2012, 34(3):3642.
[19] 鋼管混凝土结构技术规范: GB 50936—2014 [S].北京:中国建筑工业出版社,2014.
Technical code for concrete filled steel tubular structures: GB 509362014 [S].Beijing:China Architecture & Building Press, 2014. (in Chinese)
[20] 钢管混凝土结构技术规程: CECS 28:2012 [S].北京:中国计划出版社,2012.
Technical specification for concretefilled steel tubular structures: CECS 28:2012 [S].Beijing:China Planning Press, 2012. (in Chinese)
[21] 混凝土结构设计规范: GB 50010—2010 [S].北京:中国建筑工业出版社,2010.
Code for design of concrete structures: GB 500102010 [S].Beijing:China Architecture & Building Press,2010. (in Chinese)
(编辑王秀玲)

