考虑滑移和剪切变形的单箱双室组合箱梁剪力滞效应

周世军+江瑶+吴云丹+宋刚+陈晨

摘要：为准确分析单箱双室组合箱梁的剪力滞效应，考虑钢混凝土的界面滑移效应和钢腹板的剪切变形，针对顶底板和翼板定义不同的剪力滞翘曲位移函数，基于能量变分法推导出单箱双室组合箱梁剪滞效应的控制微分方程及其闭合解。以单箱双室组合箱梁算例为基础，利用该方法分析其剪力滞效应的规律，结果表明：在同时考虑滑移和剪切变形时，组合箱梁的挠度比初等梁理论解大，且其挠度随界面滑移刚度的增大而减小；组合箱梁在均布荷载作用下，滑移量与荷载值近似成正比关系；在相同条件下，钢箱梁底板的剪力滞效应较混凝土顶板显著。

关键词：组合箱梁；剪力滞；滑移；剪切变形；单箱双室

中图分类号：TU441文献标志码：A文章编号：16744764（2017）03002008

Abstract：The effect of slip of the steelconcrete interface and shear deformation of the steel webs were considered to accurately analyze the shear lag effect of the doublecell composite box girder. The different shear lag warping displacement functions for the top and bottom plates are defined. Based on energy method， the control differential equation and the closedform solution for the doublecell composite box girder are derived. As an example， the shear lag effect of a single box doublecell composite box girder is analyzed by using proposed method. The results show that the deflection of the composite box girder when considering the slip and the shear deformation is obviously larger than that obtained by the elementary beam solution， and which will decrease with the increase of interface slip stiffness. The slip value is approximately proportional to load heavy. The effect of shear lag on bottom steels lab of the box girder is more significant than that on top concrete slab.

Keywords：composite box girder； shear lag； slip； shear deformation； doublecell box girder

鋼混凝土组合箱梁因其自重轻、抗扭刚度大、结构延性高、适应现代化施工方法等优点在各类桥梁上部结构中得到了广泛应用[1]。然而，根据众多学者的研究发现，由于箱梁顶底板的剪切变形，这类结构的弯曲正应力沿梁宽方向分布不均匀，在腹板处最大，远离腹板逐渐减小，即“剪力滞后现象”。在结构设计时，如果忽略剪力滞的影响，将会低估箱梁的挠度和应力，导致结构不安全。目前，针对剪力滞常用的分析方法有能量变分法、比拟杆法、有限单元法和有限条法等[24]。

组合箱梁是由剪力连接件将钢箱梁和混凝土顶板紧密组合在一起共同受力，以充分发挥两种材料性能的结构形式。而连接件不可能绝对刚性，因此，在钢箱梁和混凝土顶板之间存在界面滑移；钢箱梁腹板的剪切变形又会引起其横截面和轴线之间的相对转动。文献[2]分析了组合箱梁应力和挠度随剪力连接件刚度变化的规律。文献[3]建立了一个同时考虑滑移和剪切变形的组合梁三维模型进行有限元分析，并通过算例和有限元分析表明剪切变形会引起组合梁位移和应力的误差。文献[4]针对薄壁箱梁提出一种考虑剪力滞效应的组合单元法，得到了组合单元的刚度矩阵，与有限元程序计算结果吻合良好，可以较为准确的考虑薄壁箱梁的剪力滞效应。学者们在分析剪力滞效应时针对剪滞翘曲位移函数提出了不同的函数形式，包括多次抛物线[46]、余弦函数[7]和椭圆曲线[8]等。

综上，学者们对组合箱梁剪力滞效应已做了许多工作，也取得了一些令人满意的结果。与此同时，一些亟待解决的科学问题也值得众多学者进行深入研究。比如：大多数以静载范围的集中荷载和均布荷载来分析剪力滞效应[23，9]，而对动载以及其他荷载共同作用下的剪力滞研究较少；剪滞翘曲位移函数具有不同的函数形式[46，78]，其精度和适用范围各有不同，而既简单又精确的函数形式值得探究；在进行力学分析时，组合箱梁的中和轴位置按初等梁理论确定[10]，为精确分析剪力滞，需探寻更为科学的方法来确定其位置；分析剪力滞效应在温度、疲劳、徐变等外界条件下的规律，对开展剪力滞效应的研究非常有必要。

目前，针对组合结构剪力滞效应的分析多局限于钢梁为工字型截面或单箱单室组合箱梁[2，11，813]，且局限于进行单因素分析，如文献[2]仅分析滑移对剪力滞效应的影响，文献[9，11]未考虑腹板剪切变形对剪力滞效应的影响，文献[12]未考虑混凝土板和钢板之间的相对滑移，而对单箱双室或多室组合箱梁进行多因素综合分析的研究较少。本文以单箱双室组合箱梁为研究对象，考虑组合箱梁的滑移效应和钢腹板的剪切变形，定义其剪滞翘曲位移函数，基于能量变分法得到单箱双室组合箱梁的控制微分方程。以典型的简支组合箱梁为例，用解析方法分析其在均布荷载下的剪力滞效应。

1基本假定

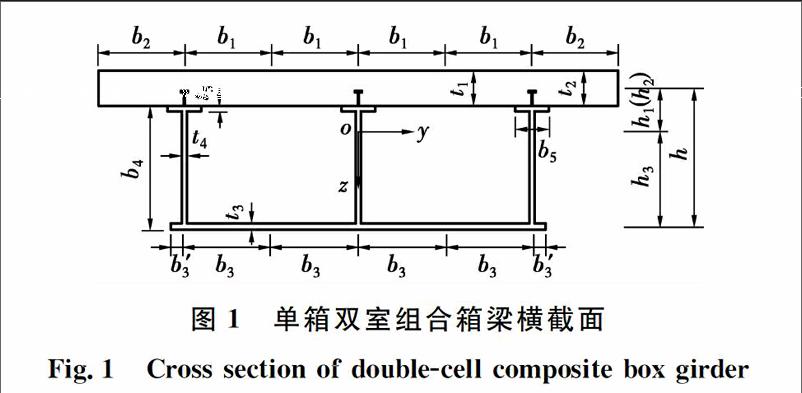
图1为等截面单箱双室组合箱梁，坐标原点取在截面形心处，坐标系采用右手螺旋法则，在均布荷载作用下，作如下假定：

混凝土顶板和钢箱梁紧密结合，竖向相对位移忽略不计，即两者竖向挠曲完全相同。

2）混凝土顶板仅考虑纵向正应变εx和剪应变γxy，其余应变均为微量，忽略不计。

3）在竖向荷载作用下，组合箱梁中和轴的位置按初等梁理论确定[10]。

4）混凝土顶板和钢箱梁的相对滑移量与剪力连接件的刚度成反比，不考虑两者之间粘结作用及横向滑移。

5）文献[9]从剪力滞效应是由于翼板剪切变形所致这一本质出发，通过分析箱梁在竖向弯曲时翼板剪力流的分布规律，提出利用翼板剪切变形规律来定义其剪滞翘曲函数的方法，本文基于此方法对顶底板和悬臂板分别定义不同的剪滞翘曲函数。文献[13]得出抛物线翘曲位移函数具有足够的计算精度，可以忽略由此在截面引起不平衡而产生的附加轴力，本文为简化计算，忽略此附加轴力。

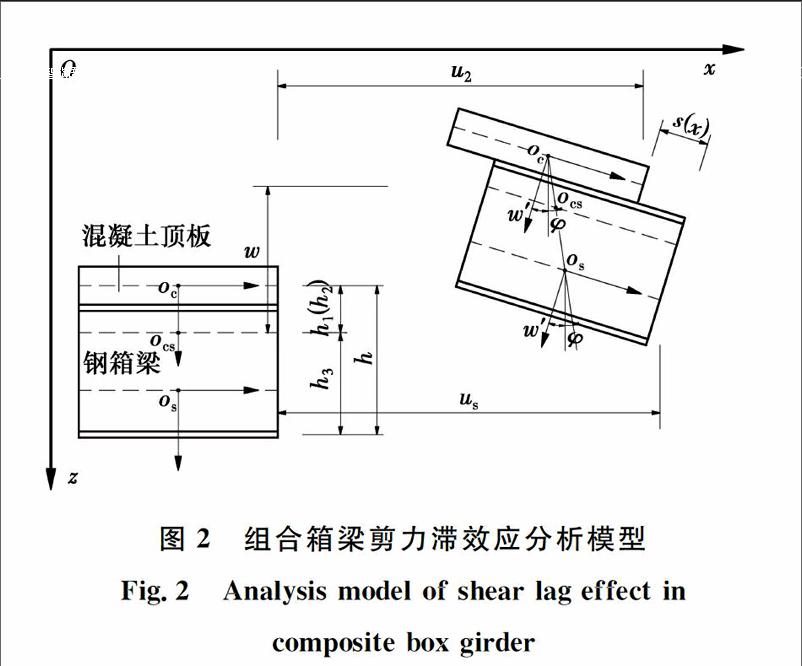
6）如图2所示，组合箱梁在竖向荷载下存在3种形式的剪切变形：钢箱梁底板和混凝土顶板因剪切变形而导致剪力滞效应；梁板之间的剪力连接件因剪切变形而产生界面滑移；钢腹板在剪力作用下产生的剪切变形使其横截面与轴线之间产生相对转动。

由图2可得，组合箱梁上任意一点的纵向位移由以上3种形式的剪切变形及弯曲变形组成，则横截面上任意一点处的纵向位移u（x，y，z）可表示为

式中：1、2、3和4分别代表混凝土顶板、悬臂板、钢箱梁底板和钢腹板相关量的下标，下同；kc、ks见式（3a）和（3b）；s（x）=us-uc为广义相对滑移量，us、uc分别为钢箱梁形心和混凝土板形心的纵向位移；h1、h2、h3分别为混凝土顶板、悬臂板和钢箱梁底板形心到组合箱梁截面形心的距离；w（x）为组合箱梁的竖向挠度；φ（x）=w′（x）-β（x）為横截面的转角；β（x）=αsQ（x）/（GsAw）为钢腹板剪切应变的平均值，αs为剪切系数，Q（x）为竖向剪力，Gs为钢箱梁的剪切模量，Aw为钢腹板的横截面面积；u（x）为纵向位移差函数；其他参数如图1所示。

根据组合箱梁轴力自平衡条件[14]，可得纵向滑移函数为Kc=-nAs/（Ac+nAs） 混凝土顶板（3a）

Ks=Ac/（Ac+nAs）钢箱梁（3b）式中：Ac、As分别为混凝土顶板和钢箱梁的横截面面积；n=Es/Ec，Es、Ec分别为钢箱梁和混凝土顶板的弹性模量。

2控制微分方程

2.1应力应变表达式

由式（1）可得混凝土顶板和钢箱梁的正应变、剪应变分别为

根据大量实验结果可知，在正常使用阶段，钢混凝土组合箱梁一般处于弹性阶段，故可对混凝土顶板、剪力连接件和钢箱梁引入线弹性的本构关系。因此，可得混凝土顶板和钢箱梁的正应力和剪应力以及剪力连接件的剪力为

式中：Gc为混凝土顶板的剪切模量；qs（z）为剪力连接件所受的剪力；Ks1为剪力连接件单位长度上的剪切滑移刚度，与混凝土顶板和钢箱梁接触面的剪力连接件的设置方式、类型和数量等因素有关。在工程应用时，剪力连接件的剪切滑移刚度可根据其复杂程度进行工程试验测得或采用《钢混凝土组合梁设计原理》中建议的k=1.0Ncv，Ncv为剪力连接件的抗剪承载力设计值。

2.2控制微分方程及边界条件

根据虚功原理，可得单箱双室组合箱梁在竖向荷载作用下的总势能为

4算例

根据上述推导结果，利用数学软件MATLAB编写程序可求解简支组合箱梁在均布荷载下剪力滞效应的相关量。模型选用时以文献[12，1516]中的组合箱梁为参考，做适当修改。本算例中的单箱双室组合箱梁截面尺寸如图4所示，简支梁计算跨径为L=4 m，材料参数为：Ec=3.45×104 MPa，Es=2.06×105 MPa，Gc=1.44×104 MPa，Gs=8.17×104 MPa，泊松比υc=0.2，υs=0.26，剪力连接件的剪切滑移刚度分别为1 000和2 000 MPa，箱梁受均布荷载q=300 kN/m作用。

4.1滑移、剪切变形及剪力滞效应对箱梁挠度的影响

图5给出了组合箱梁在均布荷载下的初等梁理论解和不同剪切滑移刚度下的本文解析解。从图中可以看出，在均布荷载作用下，滑移、剪切变形及剪力滞效应使组合箱梁的挠度增大近1.9倍，且箱梁挠度随着剪切滑移刚度的增大而减小，与文献[2，17]所得结论一致，验证了本文分析方法和公式推导的正确性。因此在结构设计时，应重视由组合箱梁界面滑移、钢腹板剪切变形和剪力滞效应引起的挠度附加值，为减小组合箱梁的挠度，可增大剪力连接件的抗剪刚度。

4.2荷载与滑移量的关系

图6、图7给出了均布荷载与组合箱梁滑移量之间的关系曲线。从图6可以看出，组合箱梁各个截面的相对滑移量随着荷载的增大而增大。滑移量在梁端达到最大值，而跨中截面为0，且滑移量从跨中截面到梁端的增大率逐渐减小，成收敛趋势，与文献[17]所得结论一致。由图7可知，在均布荷载作用下，组合箱梁的滑移量和荷载大小近似成正比。

4.3截面应力分布规律

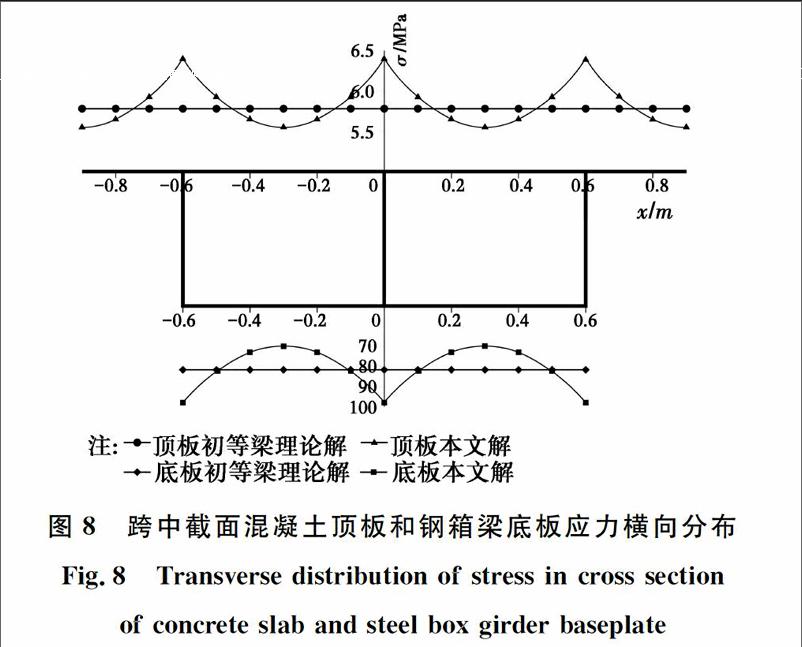
图8为跨中截面混凝土顶板和钢箱梁底板的应力横向分布，从图中可以看出混凝土顶板和钢箱梁底板的应力沿横截面均呈现明显的不均匀分布。以剪力滞系数来衡量其不均匀程度，混凝土顶板的最大剪力滞系数为1.105，钢箱梁底板最大剪力滞系数为1.201，相差近8%。表明在本文算例条件下，箱梁钢底板的剪力滞效应较混凝土顶板显著。

5结论

以单箱双室组合箱梁为研究对象，基于能量法建立了同时考虑界面滑移和钢腹板剪切变形的剪力滞效应分析方法，并得出其解析解。根据算例梁剪力滞效应分析，得出结论：

1）在考虑界面滑移和腹板剪切变形后，组合箱梁的挠度值较初等梁理论解增大较大，且挠度随着剪切滑移刚度的增大而减小，因此，在结构设计中加强钢箱梁与混凝土顶板之间的连接是非常必要的。

2）组合箱梁滑移量随荷载的增大而增大，且滑移量从梁端到跨中逐渐减小。在均布荷载作用下，其滑移量和荷载大小近似成正比。

3）在本文算例条件下，组合箱梁的剪力滞效应在箱梁钢底板与腹板交界处比混凝土顶板更加显著，在设计时应予以重视，以保证结构安全。

参考文献：

[1] MOHANNAD H M. A1SHERRAWI G A F.Effectof stiffeners on shear lag in steel box girders [J]. AlKhwarizmi Engineering Journal， 2012， 8（2）： 6376.

[2] 程海根，强士中. 钢砼组合箱梁考虑滑移时剪力滞效应分析[J]. 中国铁道科学， 2003， 24（6）： 4952.

CHENG H G， QIANG S Z. Analysis of shear lag effect of steel concrete composite box girder considering slip [J]. China Railway Science， 2003， 24 （6）： 4952.（in Chinese）

[3] 孫飞飞，李国强. 考虑滑移、剪力滞后和剪切变形的钢混凝土组合梁解析解[J]. 工程力学， 2005， 22（2）： 96103.

SUN F F， LI G Q. Analytical solution of steelconcrete composite beams considering slip， shear lag and shear deformation [J]. Engineering Mechanics， 2005， 22 （2）： 96103. （in Chinese）

[4] 骆佐龙，宋一凡，贺拴海，等.薄壁箱梁剪力滞效应分析的组合单元法[J]. 公路交通科技，2014，31（9）：5864.

LUO Z L， SONG Y F， HE S H，et al.Composite element method for analysis of shear lag effect of thin walled box girder [J]. Highway Traffic Science and Technology， 2014，31 （9）： 5864. （in Chinese）

[5] DEZI L， GARA F， LEONI G， et al. Timedependent analysis of shearlag effect in composite beams [J]. Journal of Engineering Mechanics， 2001， 127（1）： 7179.

[6] REISSNER E. Analysis of shear lag in box beams by the principle of minimum potential energy [J]. Quarterly of Applied Mathematics， 1946， 5（3）： 268278.

[7] 倪元增. 槽型宽梁的剪力滞问题[J]. 土木工程学报， 1986， 19（4）： 3241.

NI Y Z. The shear lag of the channel type wide beam [J]. China Civil Engineering Journal， 1986， 19 （4）： 3241. （in Chinese）

[8] 甘亚南，周广春. 薄壁箱梁纵向剪滞翘曲函数精度选择的研究[J]. 工程力学， 2008， 25（6）： 100107.

GAN Y N， ZHOU G C. Research on the precision selection of longitudinal shear lag warping function of thinwalled box girder [J]. Engineering Mechanics， 2008， 25 （6）： 100107. （in Chinese）

[9] 蔺鹏臻，周世军. 基于剪切变形规律的箱梁剪力滞效应研究[J]. 铁道学报， 2011， 33（4）： 100104.

LIN P Z， ZHOU S J. Study on shear lag effect of box girder based on shear deformation law [J]. Journal of Railway Science， 2011， 33 （4）： 100104. （in Chinese）

[10] SHIHTOH C. Shear lag effect in simply supported prestressed concrete [J]. Journal of Bride Engineering， 2004， 9（2）： 178184.

[11] LIN Z B，ZHAO J.Revisit of AASHTO effective flangewidth provisions for box girders [J]. Journal of Bridge Engineering， 2011， 2011（16）： 881889.

[12] 程海根，强士中. 钢混凝土组合箱梁剪力滞效应级数解[J]. 土木工程学报， 2004， 37（9）： 3740.

CHENG H G， QIANG S Z. Series solution of shear lag effect of concretecomposite box girder [J]. China Civil Engineering Journal ， 2004， 37 （9）： 3740.（in Chinese）

[13] 蔺鹏臻，周世军，刘凤奎. 抛物线型剪滞翘曲位移函数引起的附加轴力分析[J]. 工程力学， 2010， 27（8）： 9093， 119.

LIN P Z， ZHOU S J， LIU F K. Analysis of the additional axial force caused by the parabolic shear lag warping displacement function [J]. Engineering Mechanics， 2010， 27 （8）： 9093， 119. （in Chinese）

[14] 周凌宇.钢混凝土组合箱梁受力性能及空间非线性分析[D]. 长沙： 中南大学， 2004.

ZHOU L Y. The steelconcrete composite beams with nonlinear properties and spatial analysis [D]. Changsha： Central South University， 2004. （in Chinese）

[15] ZHOU W B，JIANG L Z，LIU Z J. Closedform solution for shear lag effects of steelconcrete composite box beams considering shear deformation and slip [J]. Journal of Central South University， 2012， 2012（19）： 29762982.

[16] 王連广，万江.钢与混凝土组合箱梁剪力滞效应分析[J].东北大学学报， 2015，36（8）：12041209.

WANG L G， WAN J. Analysis of shear lag effect of steel concrete composite box beam [J]. Journal of Northeastern University， 2015，36 （8）： 12041209. （in Chinese）

[17] 李法雄，聂建国.钢混凝土组合梁剪力滞效应弹性解析解[J].工程力学， 2011， 28（9）： 18.

LI F X，NIE J G. Elastic analytical solution for shearlag effect of steelconcrete composite beams [J]. Engineering Mechanics， 2011， 28 （9）： 18.（in Chinese）

（编辑王秀玲）