变截面谐振管内驻波非线性研究

郭琪磊，马 尧，宁方立

（1.中国民用航空飞行学院，航空工程学院，四川广汉618307；2.西北工业大学，机电学院，陕西西安710072）

变截面谐振管内驻波非线性研究

郭琪磊1，马 尧1，宁方立2

（1.中国民用航空飞行学院，航空工程学院，四川广汉618307；2.西北工业大学，机电学院，陕西西安710072）

基于整体轴向谐振激励下求解变截面谐振管内非线性驻波的间断Galerkin方法，研究了圆锥形谐振管内非线性驻波稳态时的瞬态特性。在圆锥形谐振管中，能够获取到无冲击的非线性驻波，验证了本方法计算圆锥形谐振管内非线性驻波的正确性，并通过提高局部逼近阶N，改善了压力波形两端的数值振荡；研究了加速度幅值a0、频率f、初始压力P0对非线性驻波压力波形和谐振管内流体流速的影响，为实现谐振管内非线性驻波应用于强声密封提供了有益思考。

谐振管；非线性驻波；Navier-Stokes方程；间断Galerkin；参数影响

谐振管内高幅值声压可应用于声压缩[1]、强声密封[2]和微机电系统[3]等工程实践中。圆柱形谐振管内非线性驻波由于具有声饱和现象，其最大声压幅值仅能达到336 kPa.相比于圆柱形谐振管，变截面谐振管能够获得更高的声压幅值，Lawrenson[1]和Ilinskii[4]于1998年分别以试验和数值仿真的方法研究了变截面谐振管内非线性驻波形成特性。其后，国内外学者对变截面谐振管内非线性驻波特性进行了深入广泛的研究。

Chun和Kim[5]在控制方程的建立中考虑了谐振管横截面积的影响，发现谐振管内驻波的非线性效应与谐振管的形状及外激励幅值的关系。Luo[3]等无量纲化谐振管尺寸，利用伽辽金方法对不同尺寸的谐振管内的非线性驻波进行了一维数值仿真，发现谐振管的各向尺寸比例关系对其内部非线性驻波幅值的影响十分显著。Li[6]等通过数值仿真的方法对谐振管形状进行优化，从而获得了高于文献[1]中的压缩比（Pmax/Pmin）。Mortell和Seymour[7]在圆锥形、指数形谐振管内获得了无冲击的压力波形，并探寻了激励幅值与频率的内在关系。

在已有研究中[8]，基于Navier-Stokes方程和理想气体状态方程，并结合Runge-Kutta方法和限制器技术，构建了一种整体轴向谐振激励下求解谐振管内非线性驻波的间断Galerkin方法，分析了不同形状谐振管内非线性驻波的各项物理性质。

本文研究整体轴向激励下圆锥形谐振管内非线性驻波稳态时的瞬态特性，对比研究不同物理参数对压力波形和流体流速的影响，为获得更高压缩比的谐振管形状优化提出了可行性建议。

1 控制方程

整体轴向激励下谐振管内流体为牛顿流体，其流动特性满足一维瞬态Navier-Stokes方程（质量守恒方程与动量守恒方程）：

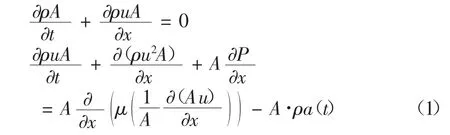
式中，ρ为流体密度；u为流体沿谐振管轴向速度；A为谐振管内节点处的截面积；t为时间；x为谐振管轴向坐标；r为谐振管径向坐标；P为压力；μ为流体动力粘度；a（t）为谐振管轴向谐振激励加速度。

上述质量守恒方程与动量守恒方程不足以求解谐振管内流体密度ρ、轴向速度u、压力P等未知量，因此引入理想气体状态方程

其中，p0为流体初始压力；ρ0为流体初始密度；γ为流体比热容比。

在空间离散过程，本文将考虑伪一维瞬态可压缩Navier-Stokes方程的向量形式

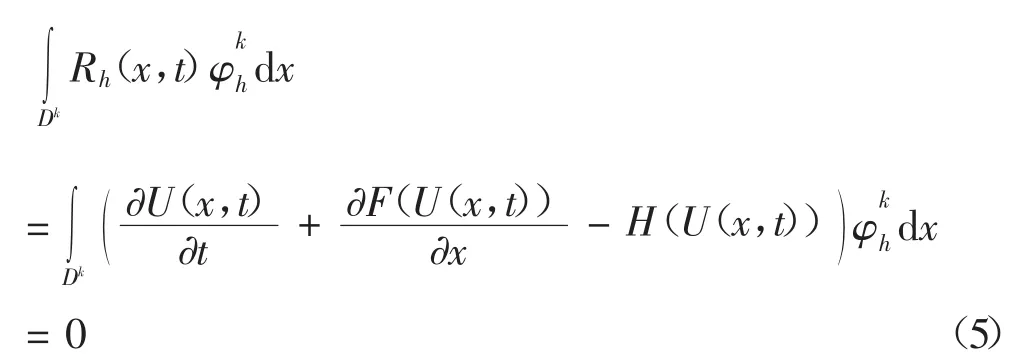
在局部单元Dk上用方程得到的解为局部近似解（x，t），并对式中空间变量进行分部积分，并用数值通量F（hx，t）*代替F（（x，t）），得到控制方程弱形式

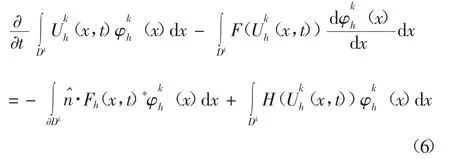
局部近似解可用如下格式表示

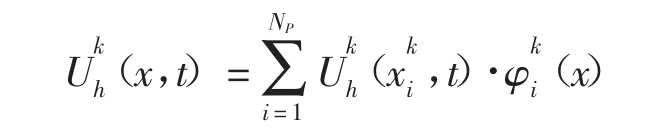
并在式中再次对空间变量进行分部积分，得到半离散格式的控制方程强形式

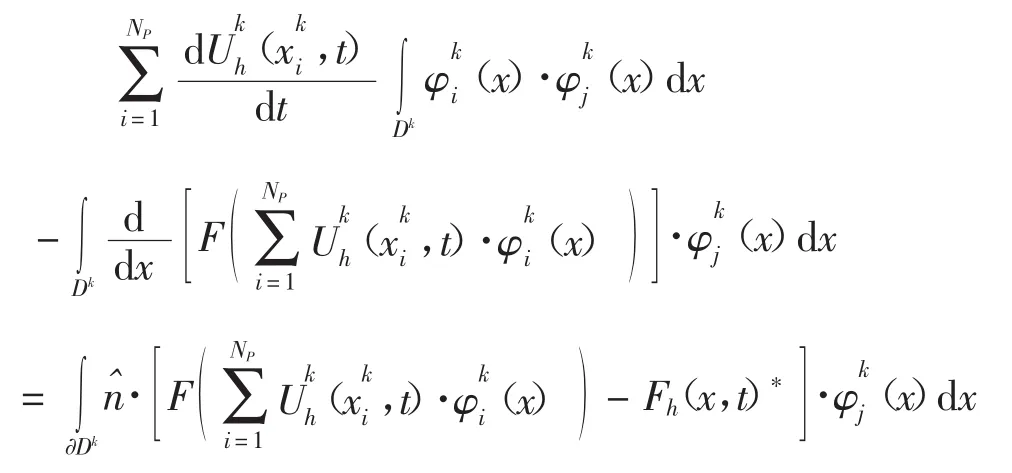
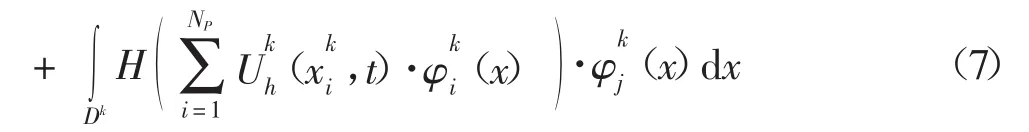
式中，Mk、Sk分别为局部质量矩阵、局部刚度矩阵，且其矩阵元素分别为（x，t）为局部节点解向量，ψ（x）局部试验函数矢量，且有

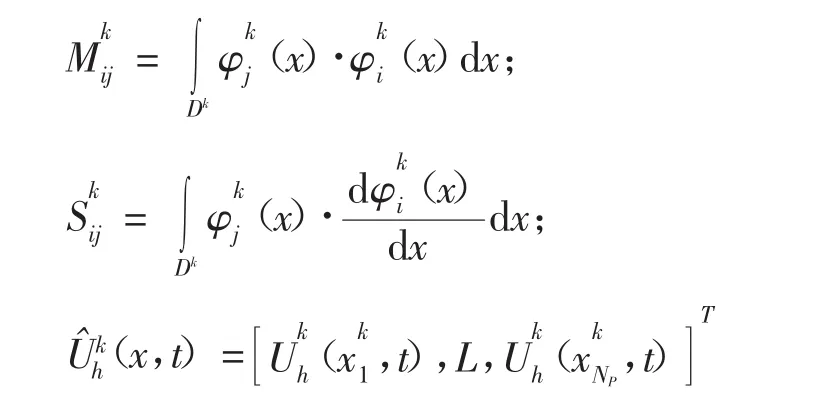
谐振管内流体初始为静止状态，并将坐标系固连于谐振管中，对谐振管两端速度施加无滑移边界条件；之后加以频率为f的整体轴向谐振激励，激励加速度为

式中，a0为激励加速度幅值。

2 数值模型

圆锥形谐振管内填充R-134气体作为工作媒质，R-134气体参数如表1所示。

表1 R-134气体参数

圆锥形谐振管形状与文献[1]中所述一致，管形函数如下：

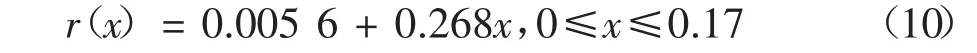
根据文献[3]，圆锥形谐振管轴向长度Lx=0.17m，谐振管小端半径R1=0.005 6 m，大端半径R2=0.044 45 m，如图1所示；根据文献[2]中关系式f=c0/（2Lx），推算得驱动谐振管的整体轴向谐振激励频率f=618Hz，并采用文献[3]中关系式a0=F0Lx（2πf），得加速度幅值为a0=1 182.5m/s2.

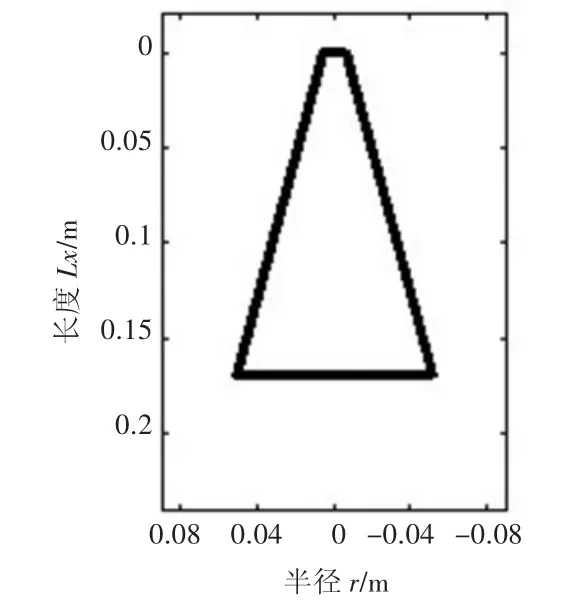
图1 圆锥形谐振管几何形状

编写数值计算程序，对圆锥形谐振管内非线性驻波进行数值仿真。选取谐振管内（X=0.0，Y=0.0）位置作为观测点，并选取局部逼近阶N=7、单元数K=250，记录圆锥形谐振管内监测点处压力、速度等物理参数。

3 数值计算结果与分析

图2（b）为局部逼近阶N=5和N=7时圆锥形谐振管内非线性驻波的两周期内压力波形。与圆柱形谐振管内压力波形出现冲击波不同[8]，圆锥形谐振管内非线性驻波的压力波形呈现出波峰尖锐、波谷平缓的特征，这与文献[4]一致，验证了本方法计算圆锥形谐振管内非线性驻波的准确性。同时，增大局部逼近阶N，改善了压力波形两端的数值振荡，从而提高计算精度。

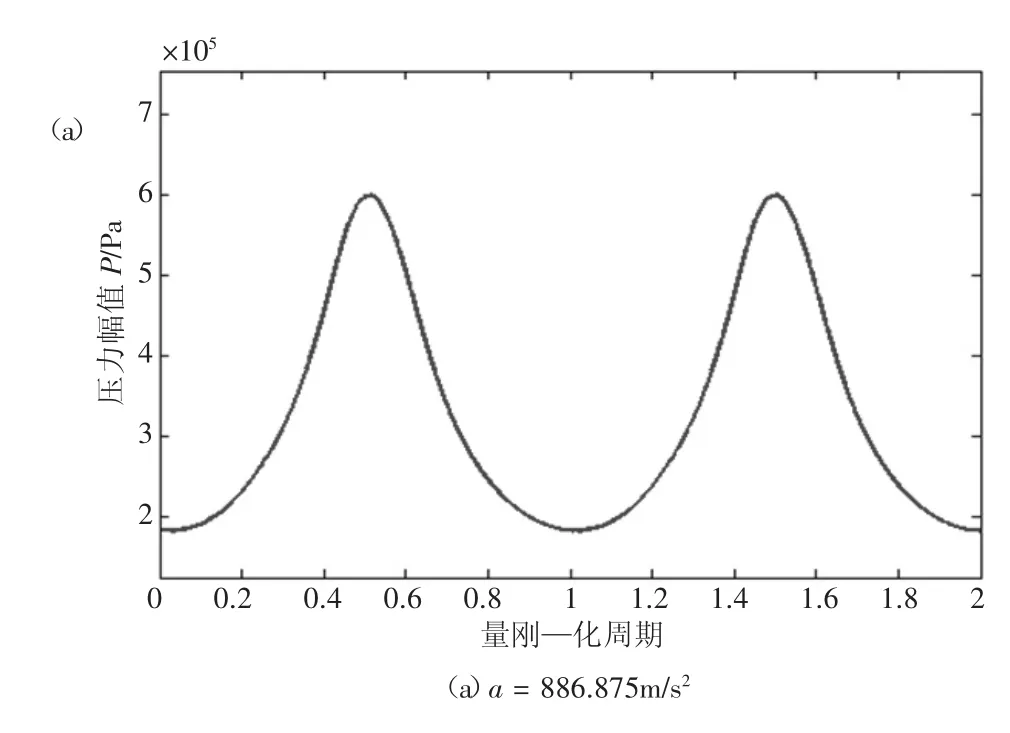
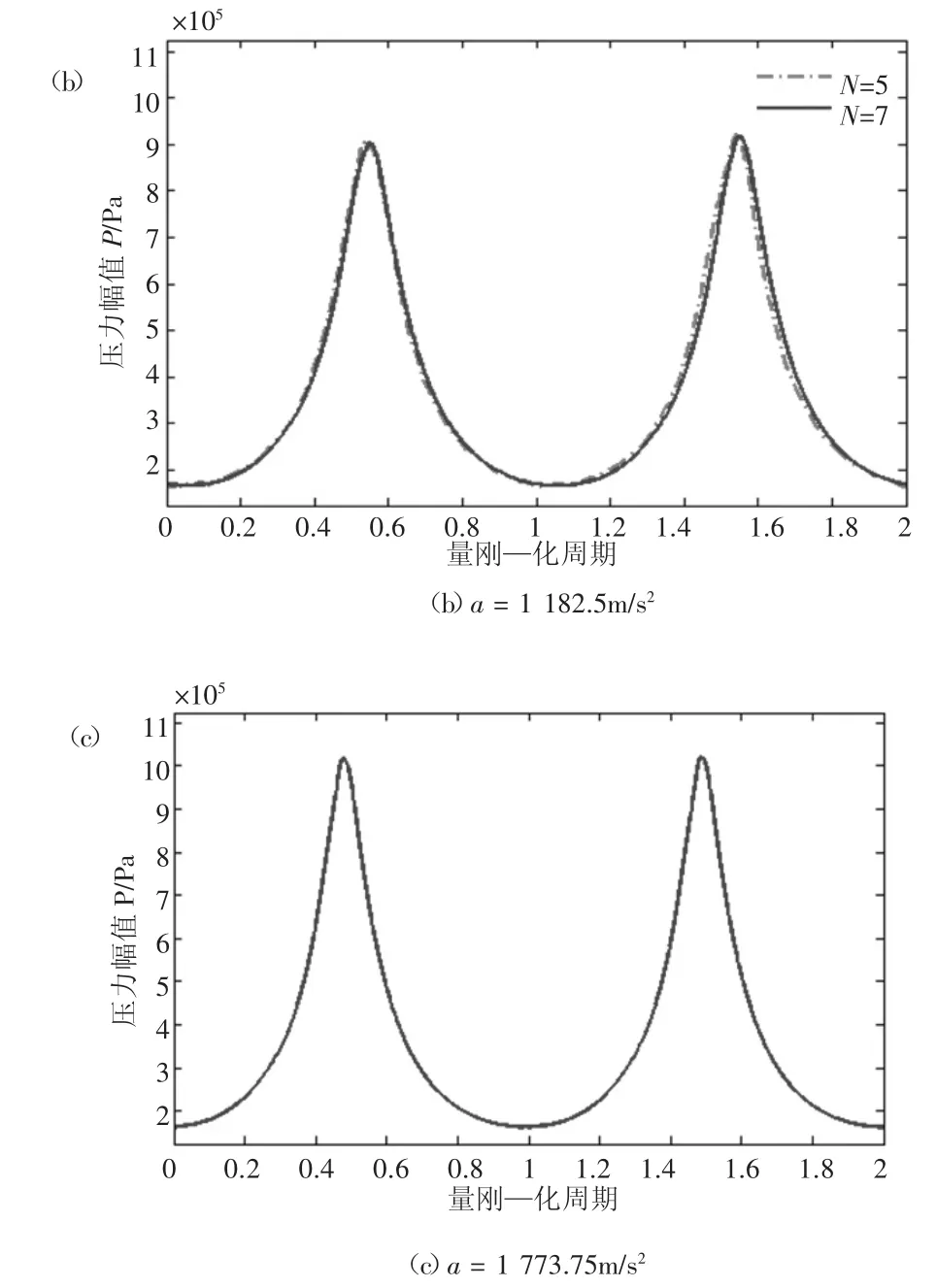
图2 不同加速度幅值下监测点处压力波形

本文还探究了加速度幅值变化对于压力波形的影响。如图2所示，随着激励加速度幅值增大，压力波形在波峰位置发生畸变，最大压力幅值逐渐升高，压缩比随之增大，压力波形整体结构也变得愈加尖锐。表2同样证明了这一结论。

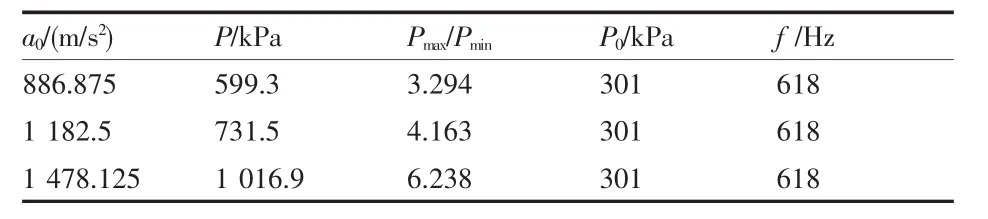
表2 不同加速度下压力幅值与最大压缩比

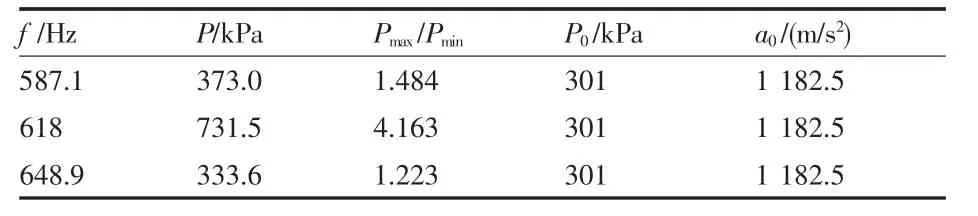
表3 不同频率下压力幅值与最大压缩比

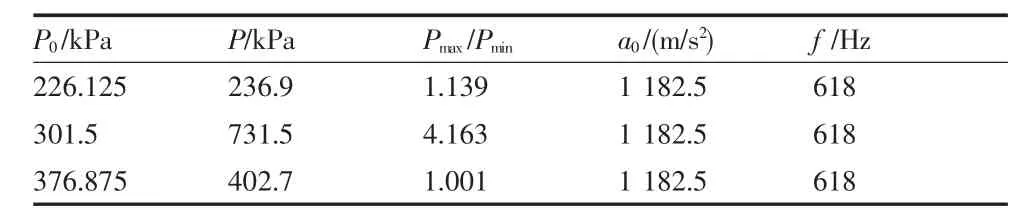
表4 不同初始压力下压力幅值与最大压缩比

为探寻频率f对非线性驻波的影响，对不同激振频率下非线性驻波进行数值计算。如表3所示，随着频率f的增加，压力幅值P和压缩比Pmax/Pmin并没有随之线性增加，而是在f=618 Hz处出现最大值：压力幅值P=731.5 kPa，压缩比Pmax/Pmin=4.13.说明该谐振管的激振频率为f=618 Hz，即此时谐振管内非线性驻波呈现无冲击波且高幅值的压力波形。

文中表4为不改变其他激励条件而选取不同初始压力P0的数值计算结果。同表3结果类似，在初始压力P0=301 kPa时，非线性驻波的压力幅值和压缩比均出现最大值。

最后，研究了稳态时不同初始参数对谐振管内流体流速的影响。图3、图4分别为不同加速度幅值和激振频率下流体流速，结果显示在不改变其他条件下，谐振管内流体流速分别在a0=1 182.5 m/s2和f =618 Hz得到最大值u=2.912 m/s.正是由于谐振管内流体具有较大流速，才能阻碍谐振管两端的气体由高压区域流向低压区域，从而达到强声密封目的。

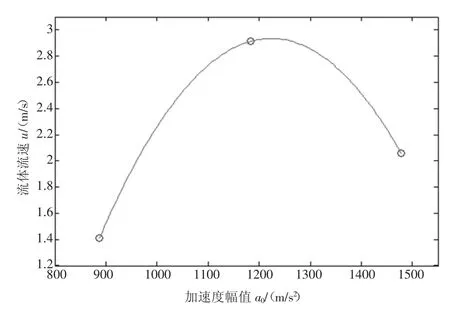
图3 不同加速度幅值下流体流速变化

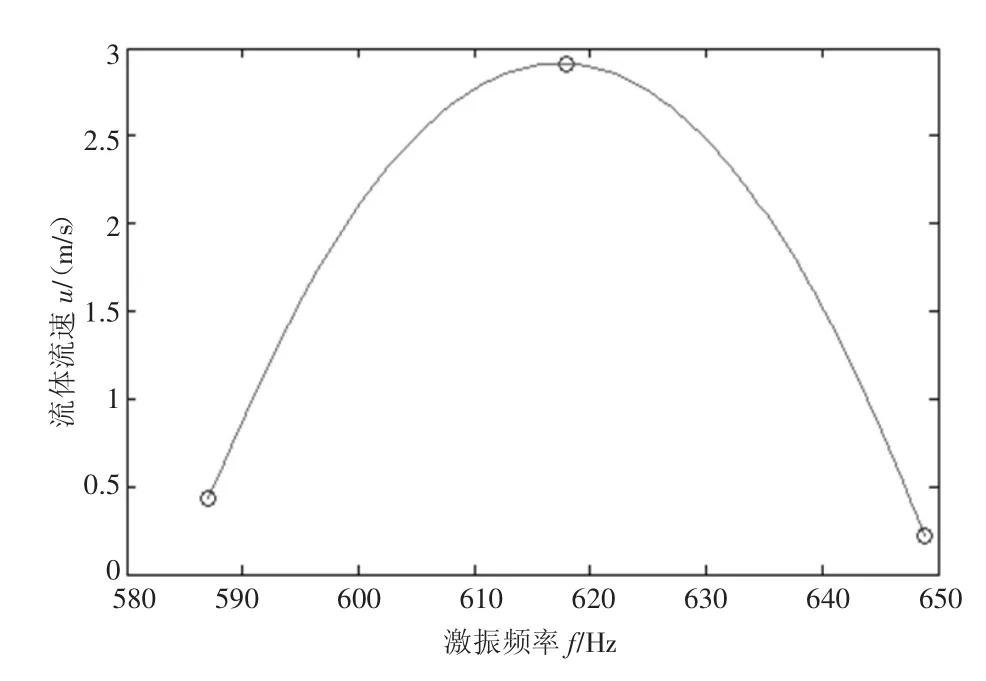
图4 不同激振频率下流体流速变化

4 结论

基于整体轴向谐振激励下求解变截面谐振管内非线性驻波的间断Galerkin方法，研究了一维圆锥形谐振管内非线性驻波稳态时的瞬态特性。在圆锥形谐振管中，能够获取到无冲击的非线性驻波，验证了本方法计算圆锥形谐振管内非线性驻波的正确性性，并通过提高局部逼近阶N，缓解了压力波形两端的数值振荡；研究了加速度幅值a0、频率f、初始压力P0对非线性驻波压力波形和谐振管内流体流速的影响，为实现谐振管内非线性驻波应用于强声密封提供了有益思考。

[1]Lawrenson C C，Lipkens B，Lucas T S.Measurements of macrosonic standing waves in oscillating closed cavities[J]. Journal of the Acoustic Society of America.1998，104（2）：623–636.

[2]Daniels C C，Steinetz B M，Finkbeiner JR，Li X F，Ra man G.Investigations of high pressure acoustic waves inres onators with swal-like features[C]//NASA Seal Secondary Air Flow System Workshop.November 5-6，2003，Cleveland，USA.

[3]Luo C，Huang X Y，Nguyen N T.Generation of shock-free pressure waves in shaped resonators by boundary driving[J]. Journal of the Acoustic Society of America，2007，121（5）：2515-2521.

[4]Ilinskii Y A，Lipkens B，Lucas T S，et al.Nonlinear stand ing waves in an acoustical resonator[J].Journal of the Acous tic Society of America，1998，104（5）：2664-2674.

[5]Chun Y D，Kim Y H.Numerical analysis for nonlinear reso nant oscillations of gas in axisymmetric closed tubes[J].Journal of the Acoustic Society of America，2000，108（6）：2765-2774.

[6]Li X，Finkbeiner J，Raman G.Optimized shapes of oscillati ng resonators for generating high-amplitude pressure waves [J].Journal of Acoustic Society of America.2004，116：2814–2821.

[7]Mortell M.P，Mulchrone K.F，Seymour B.The evolution of macrosonic standing waves in a resonator[J].International Journal of Engineering Science.2009，47：1305-1314.

[8]韦娟，宁方立，郭琪磊.谐振管内非线性驻波的间断Galerkin方法[J].机械工程学报，2016，52（23）：141-151.

Research on Nonlinear Standing Waves in Variable Cross-section Resonator

GUO Qi-lei1，MA Yao1，NING Fang-li2
（1.Civil Aviation Fight University of China，Aeronautical Engineering Institute，Guanghan Sichuan 618307，China；2.Northwestern Polytechnical University，School of Mechanical Engineering，Xi’an Shaan’xi 710072，China）

in this paper，based on the discontinuous Galerkin method for solving the nonlinear standing wave in a variable cross-section resonance tube，the transient characteristics of a nonlinear standing wave in a conical resonator are studied.In the conical resonance tube，nonlinear standing waves can get no impact，verify correctness of the conical resonance tube in the nonlinear standing wave method，and by increasing the local approximation order N，improves the numerical oscillation pressure waveform at both ends.The acceleration amplitude a0，frequency f，P0influence of initial pressure on nonlinear standing wave pressure the resonance tube flow velocity waveform，in order to achieve the resonance tube is applied to the strong nonlinear standing wave acoustic seal provides beneficial thinking.

resonators；nonlinear standing waves；Navier-Stokes equations；discontinuous galerkin；parameters affect

TH113.1

A

1672-545X（2017）04-0005-04

2017-01-24

郭琪磊（1988-），男，内蒙古呼伦贝尔人，研究生，助教，研究方向：强声密封和气动声学。