地质统计学变程优化研究
郝红瑞潘懋刘振曹凯
(北京大学地球与空间科学学院北京100871)
地质统计学变程优化研究
郝红瑞潘懋刘振曹凯
(北京大学地球与空间科学学院北京100871)
三维地质属性建模需要采用各种地质属性的样本数据,经过变异函数分析以及合适的插值算法,对未知区域进行相应插值,以获取研究区内的属性分布。为了构建更为精确的属性模型通常在建模过程中需要一定的人机交互。但在以往属性建模中,变程的有效选取一般根据属性建模的结果予以不断调整来获取,而没有一个参考的标准,这就给属性建模的效率和精度造成很大影响。针对这一问题,尝试进行地质统计学变程优化研究,寻求有效变程同相关影响因素之间的理论模型,从而提高属性建模的效率和精度。
属性建模;变异函数;有效变程;属性变化;地质体规模;序贯高斯
Class NumberP628
1 引言
三维地质属性建模的目的是获得能够表达建模区域内任意一点属性值的模型,原始数据来源于采样点样品数据的属性值,因此属性建模的核心内容是从已有样品点的属性值得到建模区域内任意一点属性值所采用的方法[1]。即在原有样品点的基础上根据一定的插值方法获得整个研究区域的属性特征。
最适用于三维地质属性建模的方法为地质统计学方法。地统计学方法中引入变异函数的概念来量化地质体内部的空间相关性,考虑研究区域的空间变异性,从而得到更为精准的属性模型。一般来说,变异函数可以由两个方面来获取:可以通过地质学专家对研究区域的专业认识来给予指导;也可以根据获取到的原始数据进行分析得到实验变异函数,再利用最小二乘法[2~4]、线性规划[5]、加权线性规划[6~7]等方法进行拟合得到表征变异性的各个参数。
但是,为了得到最佳属性模型需要不断调整变异函数中的各个参数,其中最为重要的是表征空间变异性最大距离的参数,即变程,参数不断调整的过程就会影响属性建模整体的速度,调整不当亦会影响属性建模的精度。因此,本文旨在探索地质统计学中的变程优化研究,并且给定变程与相关影响因素之间的理论模型,以期对于快速精确地构建属性建模提供一定程度的指导。
2 理论背景
地质统计学由法国统计学家G.Matheron创立,是一门以区域化变量为基础,借助变异函数来研究空间变异性和空间结构性的学科,最早应用于地质学领域。在运用地质统计学方法时需要用到一个重要工具——变异函数。变异函数代表两点之间属性值方差的二分之一,用来定量表征两点之间的相互关系,一般用块金值、基台值和变程三个参数来表达。块金值指距离无限接近0时的变异函数值;基台值是变异函数在距离大于变程时的变异函数值,用来刻画区域变量的总体变异性[8]。其中最为重要的参数为变程a。
变程是指变异函数在达到基台值时所对应的距离,即自相关距离。当距离h≤a时,两点间的属性值存在相关性,并且该相关性随着h的增大而呈现逐渐减小的趋势;而当h>a时,两点不再具有相关性。即变程a是区域变量从空间相关状态转向不相关状态的转折点。因此变程是反映区域变量变化程度的重要参数。
变程的获取通常需要三步。首先,对采样数据进行统计分析处理;然后应用常用的变异函数理论模型(球状模型、指数模型、高斯模型、空穴模型等)进行拟合,从而得到研究区域整体的变量相关关系;最后,从理论模型中得到需要的变程。但该变程只是一个理论变程,在实际应用中存在一定偏差。因此,对于构建合理的属性模型,选取一个最优变程非常关键,该变程称为有效变程。如何高效获取有效变程对于快速构建合理的属性模型起着至关重要的作用,这也是本文的研究重点。
3 有效变程获取
在研究空间变异性时通常先需要进行变异函数的拟合,然后对重要参数进行相应调整,以便更准确地刻画变量的空间变异情况。本文的有效变程获取分为拟合变异函数和校正有效变程两部分。具体过程如下。
3.1 拟合变异函数
在进行插值计算前,需要一个确定的理论变异函数,用来量化数据间的相关关系。一般采取的方法是:首先设置合适的单位滞后距,利用实验变异函数的计算公式计算对应于每个滞后距的变异函数值,即得到一系列散点图;然后,任意选取一种理论模型,其中本文中以球状模型为例说明,采用线性规划法求解变异函数模型中的各个参数,从而得到理论变异函数。具体过程如下:
1)设定合适的单位滞后距和点对数量,每个滞后距对应一个实验变异函数值,从而得到一组滞后距h和实验变异函数γ*() h的对应散点图。
2)选用一种理论模型——球状模型进行拟合,数学表达式[9~10]为
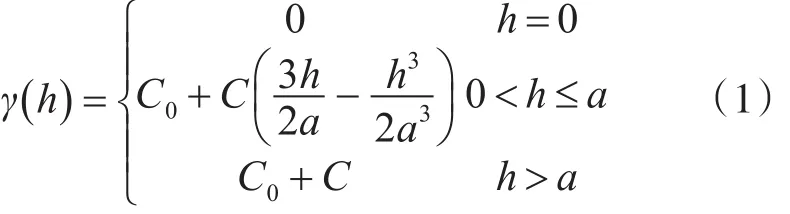
拟合变异函数即根据实验数据点对进行计算进而求取未知参数C0,C和变程a。将球状模型简化为线性函数。即令:

则球状模型简化为:y=k1+k2·h+k3·(-h3)。
将求取到的实验数据点对(hi,γ(hi))带入上述函数中,并且令
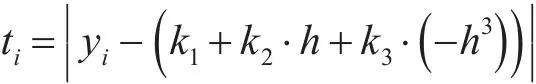
3.2 校正有效变程
由于探索空间变异程度时,首先要利用原始数据计算实验变异函数,然后进行相关的分析和拟合,进而推断出整个研究区域的空间变异性。其中,实验变异函数计算公式如下:

表示所有位置之差为向量h的两个样品点属性值之差的平方的均值的一半。由式(2)可以看出,对应不同的属性参数(如:孔隙度、渗透率、含油饱和度等)属性变化不同,求取到的变异函数亦会不同。因此,有效变程与属性的变化范围有关。
另外,除了属性变化,控制实验变异函数求取的还有一个重要参数:滞后距h,因此h的选取亦会影响到实验变异函数的准确性。通常h的选取原则为:滞后距的数量nh与滞后距h的乘积nh·h大约为被考虑方向上地质体规模的一半。因为滞后距大于地质体规模的一半时不能保证地质体中央的数据能被应用到,进而变异函数变得不稳定并且不能代表整个地质体。而且,这样长距离的变异函数在后续的地质统计学建模中也通常不需要。因此,变异函数随地质体规模的变化而变化。换句话说,有效变程与所研究地质体的规模,特别是地质体沿水平方向延伸的距离有关。为方便起见,下文均采用地质体规模代替该距离。
为寻求有效变程同属性变化和地质体规模两个参数之间的关系,得到各参数之间的理论模型,本文采用实验分析的方法进行探索,应用大量实验数据并且在不同的研究区域内进行模拟,并对结果进行相关回归分析得到最终理论模型。
3.2.1 建立有效变程理论模型
首先,选取一组测试数据进行相应试验,实验证明得到的有效变程与拟合变异函数得到的理论变程存在一定的差距,因此求取有效变程的理论模型是非常必要的。然后,对多组不同数据进行实验,并且运用回归拟合的方法得到理论模型。最后,对得到的理论模型进行验证,证明该方法的可行性。下面分别从研究思路和技术路线两方面进行阐述。
1)研究思路
本部分的测试是在长度为3.8km的区域进行,包括原始样品点97个。首先对该研究区进行三维地质构造建模,然后进行网格剖分,每个网格属性均用中心位置的属性值代替,对所有网格应用序贯高斯模拟的方法进行插值得到整个区域的属性分布情况。对测试数据进行变异函数分析拟合,得到理论变程a=1282m,并对该理论变程进行适当放大和缩小,这里以0.1的倍数逐次递增和递减,计算得到的插值结果数据与原始数据进行整体相对误差分析,以误差最小原则来获取最优变程。不同变程对应的相对误差如图1。
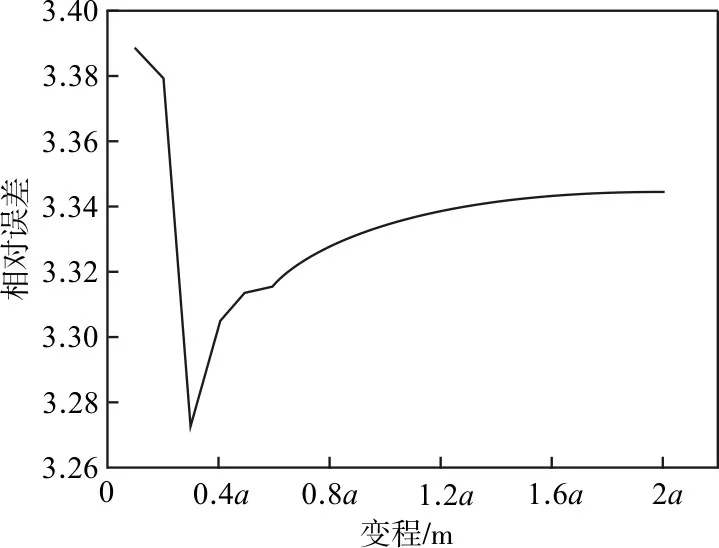
图1属性相对误差图
图1 中,横坐标代表属性建模时应用的变程大小,其中a表示理论变程,0.1a、0.2a、…、2a表示对变程适当的进行缩小和放大;纵坐标表示针对相应变程的插值结果同原始数据的整体相对误差。分析图中结果,可以得出:当变程为理论变程的0.3倍时为最低点,即插值结果与原始数据的相对误差最小;而当变程大于理论变程时会呈现误差不断增大的趋势,并且逐渐趋向平缓。由此可见,有效变程并不完全等于拟合计算出来的理论变程,而是存在一定偏差。因此研究怎样通过有限的已知变量来获取到更为合理的有效变程,对于构建精确的三维地质属性模型至关重要。
2)技术路线
由上节可知,有效变程与属性变化范围和地质体规模两个参数相关,且属性变化与地质体规模不具有相关性、即为相对独立参数,所以可以对两个参数进行线性组合。有效变程与属性变化范围和地质体规模的关系式求解方法为:首先,保持地质体规模不变,对不同类型的属性分别求解有效变程a,得到a与属性变化的相关关系;其次,保持同一种属性不变,对不同大小的研究区域分别求解有效变程a,得到a与地质体规模的相关关系;再次,将属性变化和地质体规模同时进行变化,求解方程组,得到所有权重系数。流程图如图2所示,具体步骤如下:

图2 理论模型求取流程图
(1)保持地质体规模不变,对8组不同的属性数据分别进行三维地质属性建模,以整体相对误差最小为标准来获取每种属性数据对应的有效变程。方法同上部分研究思路,每组数据均通过调整理论变程大小构建20个模型来寻找有效变程,共计构建属性模型160个。建模结果如图3(部分)。
这八组实验的原始数据属性变化范围与其对应的有效变程如表1所示,其中有效变程代表建模结果最逼近于原始数据的变程。
对这八组数据进行散点图的绘制,观察地质体大小不变时,有效变程同属性变化范围之间的关系,如图4所示。并对其进行分析拟合,得到两者之间的数学关系。
由图4可以看出,有效变程随着属性变化范围的增大而呈现逐渐减小的趋势,并且减小的幅度越来越小,形状接近于抛物线形式,即有效变程同参数属性变化大致具有二次关系,经过分析拟合处理,得到有效变程与属性变化的相关关系式为

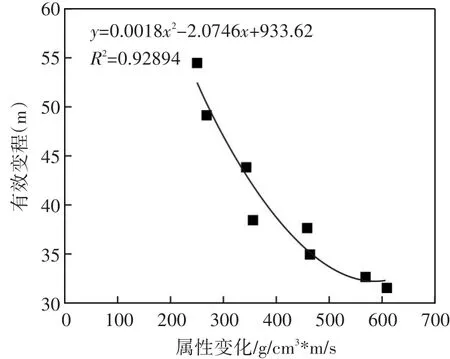
图4 有效变程同属性变化相关关系
(2)对于同一种属性,在八个不同的研究区域进行模拟,即保持属性不变,改变地质体的规模。方法同上,每组建立模型20个、共计构建属性模型160个。这八个区域的三维地质属性建模效果图如图5(部分)所示。

图5 不同区块三维地质属性建模效果图
测试数据选取了地质体规模不等的八个研究区域,对每个区域进行多次插值,对比选取使得插值结果相对原始数据整体相对误差最小的合理变程,即有效变程,不同的地质体规模与有效变程的对应如表2。

表2 地质体规模与有效变程对应表
对这八组数据进行散点图的绘制,观察同一种属性、即属性变化不变的情况下,有效变程同地质体规模之间的关系,如图6所示。

图6 有效变程与地质体规模相关关系
由图6可以看出,有效变程随地质体规模的变化呈逐渐增大的趋势,但是达到一定程度后,又逐渐减小。整体近似于正弦曲线的分布。经过分析处理以及正弦函数拟合,得到最优变程同地质体规模的相关关系为

(3)根据上述两次实验,可以总结出有效变程和属性变化呈二次关系、和地质体规模呈近似正弦关系。又由于这两个参数共同作用的效果影响最终的有效变程获取,且各部分不相关。所以将上面的两个方程进行线性组合,假定理论模型为

公式中有四个未知系数需要求取,为了估算每个参数对应的权重系数,需要求解四元一次方程组。本文通过选取不同属性值、不同研究区域的四组测试数据进行研究,为求取每组参数对应的有效变程,每组构建20个属性模型,来择优选取有效变程。共计构建属性模型80个。四组数据的属性变化、地质体规模和有效变程对应如表3。
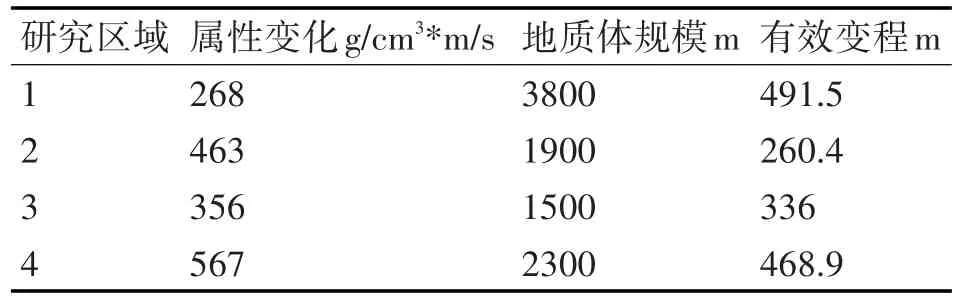
表3 属性变化、地质体规模与有效变程对应表
将前四组数据分别代入公式中,通过矩阵计算的方式求解线性方程组得到每个变量的权重系数分别为:k1=0.0057,k2=-4.99,k3=-85,k4= 1415.64。综上所述,有效变程同属性变化和地质体规模两个影响因素的最终理论模型为
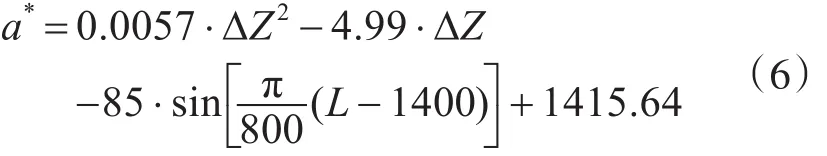
3.2.2 理论模型验证
为了验证上节得到的理论模型、即式(6)的正确性,需要对其进行结果的验证。验证过程为:选取两个不同的研究区域,并且针对两种不同的属性进行模拟,首先对其进行实验人工调整来获取有效变程,然后根据本文提出的理论模型进行计算得到有效变程,对比这两种方法得到的有效变程。来证明模型的准确性。
本节利用表4中的2组数据进行结果验证,分别将两组数据的属性变化和地质体规模带入到式(6)中,得到理论模型求取出的有效变程分别为521.1m和404.1m。而多次实验得到的结果分别为513.6m和378.7m。两组数据对应的柱状图如图7。可以看出计算出的结果同实验结果非常接近,证明该公式是正确可行的。
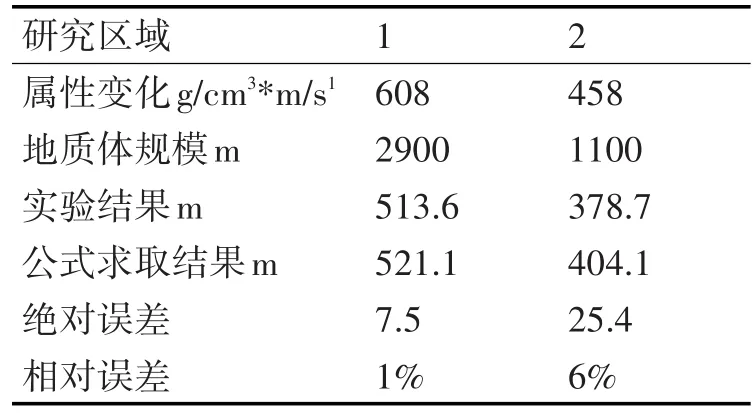
表4 验证数据
验证结果证明有效变程理论模型是可行的,并且模型的提出克服了每次建模需要不断调整参数来获取最优插值效果的问题,从而大大提高了建模的效率,也为快速地构建合理的属性模型提供一定的理论指导。
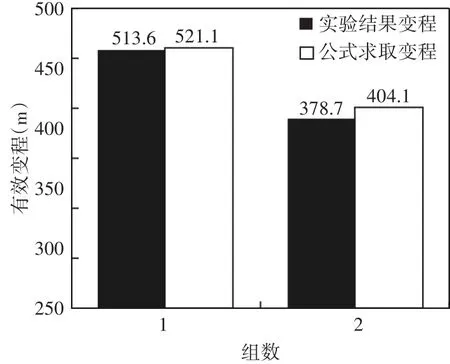
图7 公式求取结果验证图
4 实例应用
为确保结果的实用性,本文选取了安塞区王窑油田的一个区块作为实验数据予以应用。该区构造变化较为简单,构造背景为平缓的西倾单斜[11]。地层倾角为0.5°左右,埋藏深度约为1005~1060m。地质体平均孔隙度为13.7%,平均渗透率为2.27×10-3μm2,油藏平均厚度约为12m,属于低孔低渗低产油藏[12~13]。进行测试的属性数据为该区域的孔隙度参数。建模过程分为数据统计分析及预处理、拟合变异函数、邻域搜索和插值计算四部分[1,14]进行。
1)数据统计分析及预处理
在进行插值前,首先需要对原始数据进行统计分析及转换,提供平均数、最大值、最小值、峰度、偏态等多种统计量,并可进行数据转换;此外,还要对原始数据进行预处理,如异常值的剔除或样品属性值过于密集时进行适当抽稀等。计算得到该属性的属性变化范围约为0.08。
2)拟合变异函数
应用原始数据进行实验变异函数计算,并选取球状模型应用线性规划法进行变异函数的拟合。由于该区域地质体长度为6.4km,根据3.2.1节所述参数选取原则,设置滞后距为128m。
拟合出理论实验变异函数,得到理论变程为1177m,然后进行有效变程的校正,将属性变化0.08和地质体规模6.4km分别带入上节得到的公式(6)中,得到有效变程为1355m。
3)邻域搜索
对于每一个待插点,给定搜索范围,即邻域半径,并设置最大搜索点数,最大搜索点数决定最终求解的方程组个数。通过邻域搜索获取未知区域周围的原始数据,剔除与待插点距离较远相关性较弱的数据,本文选取计算出的有效变程1355m作为邻域搜索的搜索半径。对每个待估点进行邻域搜索,得到与未知点相关的样品值,用于后续待估值点的插值计算。
4)插值计算
选取合适的插值方法,如确定性建模的克里金插值法或者随机建模的序贯高斯模拟方法,得到待估点周围相关样品数据的权重值,并进行加权求和得到所有网格的属性值,最终形成连续、完整的全区三维地质属性模型。本文采取序贯高斯模拟方法对每个待插点进行随机模拟,序贯高斯模拟[15~18]是一种基于高斯场的序贯模拟方法,多用于符合高斯分布的连续型变量(如孔隙度、渗透率、饱和度等),能够给予不确定性评价,并且相较克里金插值[19~20]更能真实地反映地质情况,因此应用非常广泛。插值完成最终得到的属性建模效果图如图8所示。

图8 王窑区属性建模效果图
5 结语
1)通过实验数据回归分析、拟合的方法得到有效变程同属性变化以及地质体规模两个参数之间的理论数学模型,从而更加快速地获得有效变程,为更加高效地构建合理、精确的三维地质属性模型提供理论指导。
2)将该方法应用到油田的实际工作中,获得更为合理的建模结果。能更好地为油藏数值模拟提供数据准备,也为致密砂岩地质体的评价与预测、水平井井段优化设计等方面提供可靠的依据,有一定的应用价值。
3)研究得到的有效变程理论模型针对所有的地质统计学方法均适用,因此可以应用于矿产资源预测和评价、矿山地质与矿产经济、石油地质与煤田地质勘探与开发、水文工程地质等多个领域,具有很强的普适性。
[1]吴耕宇.基于规则网格的三维地质属性建模关键技术研究[D].北京:北京大学,2015.
WU Gengyu.Research on key technology of 3D geological attribute modeling based on regular grid[D].Beijing:Peking University,2015.
[2]Cressie N.Fitting variogram models by weighted least squares[J].Jounal Of The International Association For Mathematical Geology,1985,17(5):563-586.
[3]黄沧钿.变异函数的自动拟合方法[J].新疆石油地质,2001,22(2):155-157.
HUANG Cangdian.Automatic fitting method of variation function[J].Xinjiang Petroleum Geology,2001,22(2):155-157.
[4]孙洪泉.地质统计学及其应用[M].徐州:中国矿业大学出版社,1990:20-45.
SUN Hongquan.Geological statistics and its application[M].Xuzhou:China Mining University Press,1990:20-45.
[5]胡小荣,俞茂宏.理论变异函数球状模型的加权线性规划法拟合[J].地质与勘探,2001(5):45-48.
HU Xiaorong,YU Maohong.Weighted linear programming method for the spherical model of the theoretical variation function[J].Geology And Exploration,2001(5):45-48.
[6]程勖,杨毅恒.变差函数中加权系数拟合方法的改善[J].地球物理学进展,2009,24(1):362-366.
CHENG Xu,YANG Yiheng.Improvement of fitting method of weighted coefficient in variation function[J].Progress In Geophysics,2009,24(1):362-366.
[7]滕召良,吕文生,杨鹏,等.基于加权线性规划法的变异函数球状模型自动拟合研究[J].西部探矿工程,2014,26(9):73-76.
TENG Zhaoliang,LV Wensheng,YANG Peng,et al.Automatic fitting of the spherical model of the variation function based on the weighted linear programming method[J].West-China Exploration Engineering,2014,26(9):73-76.
[8]张仁铎.空间变异理论及应用[M].北京:科学出版社,2005:13-18.
ZHANG Renduo.Spatial variability theory and its application[M].Beijing:Science Press,2005:13-18.
[9]PYRCZ M J,DEUTSCH C V.Geostatistical reservoir modeling[M].New York:Oxford University Press,2002:40-70.
[10]DEUTSCH C V,JOURNEL A G.GSLIB Geostatistical software library and user's guide[M].New York:Oxford University Press,Second edition,1998:11-14.
[11]田丰.安塞油田王窑区长6地质体微观特征及气驱提高采收率研究[D].西安:西安石油大学,2013.
TIAN Feng.EOR research on microscopic characteristics and 6 gas geological body of Ansai oilfield Wangyao district[D].Xi'an:Xi'an Petroleum University,2013.
[12]赵向原,曾联波,靳宝光,等.裂缝性低渗透砂岩油藏合理注水压力——以鄂尔多斯盆地安塞油田王窑区为例[J].石油与天然气地质,2015(5):855-861.
ZHAO Xiangyuan,ZENG Lianbo,JIN Baoguang,et al. Rational water injection pressure in fractured low permeability sandstone reservoir——A case study of Ansai oil field in Ordos Basin[J].Petroleum And Natural Gas Geology,2015(5):855-861.
[13]许永涛,朱玉双,张洪军,等.安塞油田王窑区长6储层特征及孔渗特性控制因素[J].石油地质与工程,2011,25(4):25-28.
XU Yongtao,ZHU Yushuang,ZHANG Honghui,et al. The characteristics of controlling factors of Ansai oilfield infiltration Wangyao 6 reservoir characteristics and hole[J].Petroleum Geology and Engineering,2011,25(4):25-28.
[14]姚凌青.基于地质统计学的三维属性建模方法研究[D].北京:北京大学,2008.
YAO Lingqing.Research on the method of 3D attribute modeling based on geo statistics[D].Beijing:Peking University,2008.
[15]赵彦锋,孙志英,陈杰.Kriging插值和序贯高斯条件模拟算法的对比分析[J].地球信息科学学报,2010,12(6):767-776.
ZHAO Yanfeng,SUN Zhiying,CHEN Jie.Comparison and analysis of Kriging interpolation and sequential Gauss conditional simulation algorithm[J].Journal of Earth Information Science,2010,12(6):767-776.
[16]BOISVERT J B,DEUTSCH C V.Programs for kriging and sequential Gaussian simulation with locally varying anisotropy using non-Euclidean distances[J].Computers And Geosciences,2011,37(4):495-510.
[17]胡先莉.序贯条件模拟方法研究及应用[D].成都:成都理工大学,2007.
HU Xianli.Research and application of sequential conditional simulation method[D].Chengdu:Chengdu University of Technology,2007.
[18]姚兴苗.各向异性序贯高斯随机模拟研究[D].成都:电子科技大学,2014.
YAO Xingmiao.Anisotropic sequential Gauss simulation[D].Chengdu:University of Electronic Science and Technology,2014.
[19]张靖.基于克里金算法的点云数据插值研究[D].西安:长安大学,2014.
ZHANG Jing.Study on Kriging algorithm of point cloud data based on interpolation[D].Xi'an:Chang'an University,2014.
[20]王亭.顾及各向异性的三维Kriging空间插值方法研究[D].南京:南京师范大学,2013.
WANG Ting.Research on 3D Kriging spatial interpolation method considering anisotropy[D].Nanjing:Nanjing Normal University,2013.
Variable Range Optimization in Geostatistics
HAO HongruiPAN MaoLIU ZhenCAO Kai
(School of Earth and Space Sciences,Peking University,Beijing100871)
It is necessary to adopt sample data of various geological attributes for 3D geological attribute modeling,the interpolation of unknown regions is performed by variogram analysis and proper interpolation algorithm to obtain the distribution of attributes in the study area.In order to build more accurate attribute models,a certain amount of human-computer interaction is usually needed during the modeling process.But in the past property modeling,the effective selection of variable range is usually adjusted according to the result of attribute modeling,without a reference standard,and this has great influence on the efficiency and precision of attribute modeling.Based on the problems above,this paper attempts to study the optimization of geostatistical variable range,and seek the theoretical model between effective variable range and related influencing factors,so as to improve modeling efficiency and accuracy.
attribute modeling,variation function,effective variable range,attribute change,geological scale,sequential Gaussian
P628
10.3969/j.issn.1672-9722.2017.06.035
2016年12月3日,
2017年1月30日
国家自然科学基金项目“基于语义的多分辨率储层数据组织与管理”(编号:41472113)资助。
郝红瑞,女,硕士研究生,研究方向:三维地质属性建模及插值算法。潘懋,男,博士,教授,研究方向:石油地质、环境地质和信息地质。刘振,男,博士研究生,研究方向:地应力建模及岩石力学参数建模。曹凯,男,博士研究生,研究方向:三维地质构造建模和相建模。

