如何培养学生的数学思维能力
吉林省汪清县第六中学 姜之宇
思维是认知的核心成分,是人脑对事物本质和事物之间规律性关系概括的间接的反映。思维的发展水平决定着整个知识系统的结构和功能。高中生一般年龄为15—18岁,处于青年初期。他们的身心急剧发展、变化和成熟,学习的内容更加复杂、深刻,生活更加丰富多彩。这种巨大的变化对高中生的思维发展提出了更高的要求。作为高中数学教师,应抓住学生思维发展的飞跃时期,利用成熟期前可塑性大的特点,做好思维品质的培养工作,使学生的思维得到更好的发展。
一、高中学生数学思维障碍的形成原因
根据布鲁纳的认识发展理论,学习本身是一种认识过程,个体的学习总是要通过已知的内部认知结构,对“从外到内”的输入信息进行整理加工,以一种易于掌握的形式加以储存。但是这个过程并非总是一次性成功。一方面,如果教师在教学过程中,不顾学生的实际情况(即基础)或不能觉察到学生的思维困难之处,而是按自己的思路或知识逻辑进行灌输式教学,则到学生自己去解决问题时往往会感到无所适从;另一方面,当新的知识与学生原有的知识结构不相符或新旧知识间缺乏必要的媒介时,这些新知识就会被排斥或经“校正”后吸收。因此,如果教师的教学脱离学生的实际或学生在学习过程中新旧知识不能顺利交接,那么势必会造成学生对所学知识认知上的不足、理解上的偏颇,从而在解决具体问题时就会产生思维障碍,影响学生解题能力的提高。
二、高中学生数学思维障碍的解决策略
(一)激发学生学习兴趣,提高数学探究思维
兴趣能够调动学生的思维。在课堂教学中,我们应该适当选择学生感兴趣的教学方法,激发学生对数学产生浓厚的兴趣,使他们乐意学;并及时给予表扬和鼓励,使他们开心地学,这样他们的思维能力才能最大限度地活跃起来。这种以“兴趣”助长思维不仅培养了学生学习数学的兴趣,也达到了数学教学的真正目的。
(二)培养独立的思维能力,学会自主学习
在传统的应试教育思想的束缚下,学生从小学到中学的学习几乎完全依赖于老师,只按照老师和书本之导向去记忆和容纳知识;学生既缺少创造性思维,也缺乏相应训练,因此创造心理逐渐淡化,养成了依赖思维心理。基于此,培养独立思维心理对于一个学生来说是当务之急。
首先,让学生学会不盲从。其次,要让学生对学问进行大胆合理的怀疑。这一点是培养独立性思维的核心。大胆的怀疑是创造人才的一个标志,是独立思考的体现,只有大胆合理地怀疑,才能进行科学的创造。
(三)培养发散思维,提高思维灵活性
发散思维是理解教材、灵活运用知识所必须的,也是迎接信息时代、适应未来生活所应具备的能力。因此,在学生较好地掌握了一般方法后,要注意诱导学生离开原有思维轨道,从多方面考虑问题;当学生思路闭塞时,要善于调度原型帮助学生接通与有关旧知识和解题经验的联系,作出转换、假设、化归、逆反等变通,产生多种解决问题的设想。
例:已知圆的方程x2+y2=r2,求经过圆上一点p(x0,y0)的切线方程。
法一:常规法已知点求斜率。
法三:代数法,设出直线方程,然后利用直线和圆相切直线与圆联立所得一元二次方程有两个相等的实数根,即判别式为零,可得答案
法四:几何法,当直线和圆相切时,利用圆心到直线的距离等于r。
(四)培养创造性思维,让数学生动活泼起来
1.发挥学生的想象能力,培养学生的直觉思维
爱因斯坦根据自己亲身经历的科学创造实际得出结论,“我相信直觉和灵感。”他一再强调,在科学创造过程中,从经验材料到提出新思想之间,没有“逻辑的桥梁”,必须诉诸灵感和直觉。因此在学生直觉思维能力的培养中,观察能力的培养甚为重要。
比如,在立体几何中,设计等体积的正方体、等边圆柱体、球体哪一个表面积最小?让学生凭直觉回答后再证明。再比如讲“等差数列”的概念时,可以让学生填空:(1)1,4,7,_ ,13,_ ; (2)3,0,_,-6,_,_; 让观察与思维有机结合,分析与猜测同步进行。
2.拓宽思维的广度,培养学生的思维转换能力
恩格斯曾说过:“由一种形式转化为另一种形式不是无聊的游戏而是数学的杠杆,如果没有它,就不能走很远。”数学建模就是把实际问题转换成数学问题,如果我们在数学教学中注重转化,用好这根有力的杠杆,对培养学生思维品质的灵活性、创造性及开发智力、培养能力、提高解题速度是十分有益的。
例:某厂2001年生产利润逐月增加,且每月增加的利润相同,但由于厂方正在改造建设,元月份投入资金建设恰好与元月的利润相等,随着投入资金的逐月增加,且每月增加投入的百分率相同,到12月投入建设资金又恰好与12月的生产利润相同,判断全年总利润m与全年总投入N的大小关系是_______.
分析:每月的利润组成一个等差数列且公差d>0,每月的投资额组成一个等比数列{bn},且公比q>1。a1=b1,且a12=b12,比较S12与T12的大小。 若直接求和,很难比较出其大小,但注意到等差数列的通项公式是关于n的一次函数,其图象是一条直线上的一些点列。等比数列的通项公式是关于的指数函数,其图象是指数函数上的一些点列。
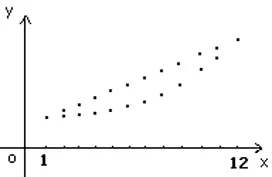
在同一坐标系中画出图象,直观地可以看出ai≥bi,则S12>T12,即m>N。本道题把一个原本是求和的问题,退化到各项的逐一比较大小,而一次函数、指数函数的图象又是学生们所熟悉的。在对问题的化归过程中进一步挖掘了问题的内涵,通过对问题的反思、再加工,使问题直观、形象,使解答更清新。学生对这类问题的进一步研究,无疑会激发其学习数学的主动性,且能开拓学生创造性思维能力,养成善于发现问题,独立思考的习惯。
当前,素质教育已经向我们传统的高中数学教学提出了更高的要求。但要真正培养学生的数学思维能力,光凭传授知识是远远不够的,重要的是在教学中必须坚持以学生为主体,以培养学生的思维能力为出发点,积极调动学生的主观能动性,引导其自觉地在学习中进行求异思维活动,培养学生善于思考、独立思考的品质。只有这样才能使学生分析和解决问题的能力得到长足的进步,创新能力得到真正提高,使学生学到有用的数学。

