高二第二学期期末测试题
■河南省新郑市一中分校 韩志刚
高二第二学期期末测试题
■河南省新郑市一中分校 韩志刚
一、选择题(本大题共1 2小题,每小题5分,共6 0分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
A.-i Bi.
C.-1 D.1
A.P>Q B.P=Q C.P<Q D.由a的取值确定
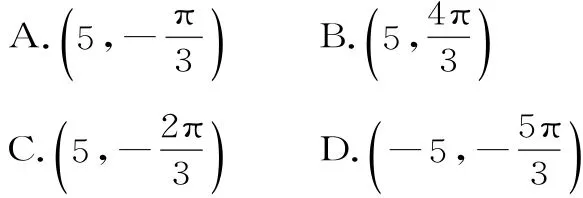
4.有一段“三段论”,推理是这样的:对于可导函数f(x),如果f'(x0)=0,那么x= x0是函数f(x)的极值点。因为f(x)=x3在x=0处的导数值f'(0)=0,所以x=0是函数f(x)=x3的极值点。以上推理中( )。
A.大前提错误 B.小前提错误C.推理形式错误 D.结论正确
5.已知z是复数z的共轭复数,z+z+ z·z=0,则复数z在复平面内对应的点的轨迹是( )。
A.圆 B.椭圆
C.双曲线 D.抛物线
A.仅有最小值的奇函数
B.仅有最大值的偶函数
C.既有最大值又有最小值的偶函数
D.非奇非偶函数
7.用数学归纳法证明“(n+1)(n+2)…(n+n)=2n·1·2…(2n-1)(n∈N*)”时,从“n=k到n=k+1”时,左边应增添的式子是( )。
A.2k+1 B.2k+3
C.2(2k+1) D.2(2k+3)
8.以下命题,正确命题的个数为( )。
(1)化极坐标方程ρ2c o sθ-ρ=0为直角坐标方程为x2+y2=0或y=1。
(2)集合A={x||x+1|<1},B= {x|y=-2x-x2},则A⊆B。
(3)若函数y=f(x)在区间(a,b)内可导,且x0∈(a,b),则的值为2f'(x0)。
(4)若曲线y=ex+a与直线y=x相切,则a的值为0。
(5)将点P(-2,2)变换为P'(-6,1)的伸缩变换公式为
A.1 B.2 C.3 D.4
9.下列积分值等于1的是( )。

1 0.给出下列四个命题:①f(x)=x3-3x2是增函数,无极值;②f(x)=x3-3x2在(-∞,2)上没有最大值;③由曲线y=x,y =x2所围成图形的面积是;④函数f(x) =l nx+a x存在与直线2x-y=0垂直的切线,则实数a的取值范围是中正确命题的个数为( )。
A.1 B.2
C.3 D.4
1 1.已知点列如下:P1(1,1),P2(1,2), P3(2,1),P4(1,3),P5(2,2),P6(3,1), P7(1,4),P8(2,3),P9(3,2),P10(4,1), P11(1,5),P12(2,4),…,则P60的坐标为( )。
A.(3,8) B.(4,7)
C.(4,8) D.(5,7)
A.[1,+∞) B.(0,+∞) C.[0,+∞) D.(1,+∞)
二、填空题(本大题共4小题,每小题5分,共2 0分。)
1 3.已知函数f(x)=x3+3m x2+n x+ m2在x=-1时有极值0,则m+n=。
1 4.已知函数y=f(x)的图像在点M(1, f(1))处的切线方程是+f'(1)=。
1 6.若函数f(x)=x3+3x对任意的m∈[-2,2],f(m x-2)+f(x)<0恒成立,则x∈。
三、解答题(本大题共6小题,共7 0分,解答应写出文字说明、证明过程或演算步骤。)
1 7.(本小题满分1 0分)
写出圆心的极坐标,并求当r为何值时,圆O上的点到直线l的最大距离为3。
1 8.(本小题满分1 2分)
已知函数f(x)=x2+al nx的图像与直线l:y=-2x+c相切,切点的横坐标为1。
(1)求函数f(x)的表达式和直线l的方程;
(2)若不等式f(x)≥2x+m对f(x)的定义域内的任意x恒成立,求实数m的取值范围。
1 9.(本小题满分1 2分)
已知函数f(x)=al nx-2a x+ 3(a≠0)。
(1)设a=-1,求函数f(x)的极值;
2 0.(本小题满分1 2分)
在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρs i n2θ=ac o sθ(a>0),过点P(-2,-4)的直线l的参数方程为为参数),直线l与曲线C相交于A,B两点。
(1)写出曲线C的直角坐标方程和直线l的普通方程;
(2)若|P A|·|P B|=|A B|2,求a的值。
2 1.(本小题满分1 2分)
已知定义在(0,+∞)上的三个函数f(x)=l nx,g(x)=x2-a f(x),h(x)= x-ax,且g(x)在x=1处取得极值。
(1)求a的值及函数h(x)的单调区间。
(2)求证:当1<x<e2时,恒有x<
2 2.(本小题满分1 2分)
(1)当a=1时,求f(x)在区间[1,e]上的最大值和最小值;
(2)若在区间(1,+∞)上,函数f(x)的图像恒在直线y=2a x下方,求a的取值范围。
参考答案与提示
1.C 2.C 3.A 4.A 5.A 6.C 7.C 8.A 9.D 1 0.B 1 1.D 1 2.B
1
因此,f(x)=x2-4 l nx,f(1)=1,切点为(1,1),所以c=3。
直线l的方程为y=-2x+3。
经判断g(x)在(0,2]上是减函数,在[2,+∞)上是增函数。
g(x)min=g(2)=-4 l n2,所以m≤g(x)min=-4 l n 2。
因此,当f(x)≥2x+m在f(x)的定义域内恒成立时,实数m的取值范围是-∞,-4 l n 2 ( ]。
因为g(x)在区间(1,3)上不是单调函数,且g'(0)=-1,所以
2 0.(1)由ρs i n2θ=ac o sθ(a>0)得ρ2s i n2θ=aρc o sθ(a>0),所以曲线C的直角坐标方程为y2=a x(a>0)。
直线l的普通方程为y=x-2。
(2)将直线l的参数方程代入曲线C的直角坐标方程y2=a x(a>0)中,得:
t2-2(a+8)t+4(a+8)=0。
设A,B两点对应的参数分别为t1,t2,则有t1+t2=2(a+8),t1·t2=4(a+8)。
因为|P A|·|P B|=|A B|2,所以(t1-t2)2=t1·t2,即(t1+t2)2=5t1·t2。
解得a=2或a=-8(舍去)。
2 1.(1)g(x)=x2-a f(x)=x2-al nx,
所以a=2。
(2)因为1<x<e2,所以0<l nx<2,即2-l nx>0。
当x>1时,k'(x)>0,所以k(x)在(1, +∞)上是增函数,所以k(x)>k(1)=0, k(x)>0,即
对于x∈[1,e],有f'(x)>0,所以f(x)在区间[1,e]上为增函数。
在区间(1,+∞)上,函数f(x)的图像恒在直线y=2a x下方等价于g(x)<0在区间(1,+∞)上恒成立。

此时g(x)在区间(x2,+∞)上是增函数,并且在该区间上有g(x)∈(g(x2), +∞),不合题意。
当x2<x1=1,即a≥1时,同理可知, g(x)在区间(1,+∞)上,有g(x)∈(g(1), +∞),也不合题意。
(责任编辑 徐利杰)

