有色金属期货市场分形特征研究
林 杰,龚 正
(同济大学 经济与管理学院,上海 200092)
有色金属期货市场分形特征研究
林 杰,龚 正
(同济大学 经济与管理学院,上海 200092)
通过重标极差分析方法,使用了“十二五”期间的市场交易数据,对沪铜和沪铝两种有色金属期货品种的分形特征进行了实证研究,结果表明,两种有色金属期货品种价格收益率时间序列存在波动集聚性与非线性,并具有反持久性和长期记忆性的分形特征,是一个有偏的随机游走过程。这两种有色金属期货品种分别具有545天和572天不同的长期记忆周期,反映了系统的平均循环长度,H指数分别为0.389和0.408,表明我国有色金属期货市场尚未达到弱式有效。
有色金属期货;重标极差分析;分形特征;反持久性;长期记忆性
一 引 言
分形指的是以非整数维形式充填空间的形态特征。1973年,B.B.Mandelbrot在法兰西学院讲课时,首次提出了分维和分形的设想。分形是一个数学术语,也是一套以分形特征为研究主题的数学理论。分形理论既是非线性科学的前沿和重要分支,又是一门新兴的横断学科,是研究一类现象特征的新的数学分科,相对于其几何形态,它与微分方程与动力系统理论的联系更为显著[1]。分形的自相似特征可以是统计自相似,构成分形也不限于几何形式,时间过程也可以。分形几何是一门以不规则几何形态为研究对象的几何学。由于不规则现象在自然界普遍存在,因此分形几何学又被称为描述大自然的几何学。分形几何学建立以后,很快就引起了各个学科领域的关注,不仅在理论上,而且在实用上分形几何都具有重要价值[2]。
20世纪80年代以来,分形广泛应用于资本市场中,揭示了价格行为的持久性、长期记忆性、自相似性,局部随机和整体有序共存的分形特征,为资本市场价格行为和定价有效性提供了新的研究方向。Peters(1994)[3]提出“分形市场理论”(Fractal Market Theory,FMT),并发现了Dow Jones和S&P500日、周、月、年之间的收益曲线的“自相似性”,证明时间序列中存在自相似性和标度不变性。Peng、Buldyrev(1994)[4]在研究核糖核酸行为机制过程中提出消除趋势波动分析方法(DFA),现已广泛应用于各个领域,成为检验非平稳时间序列长期相关特征的重要工具。Kantelhardt(2002)[5]在单分形DFA的基础上,与基于标准配分函数的多重分形体系结合,提出了多重分形消除趋势波动分析方法(Multifractal Detrended Fluctuation Analysis,MF-DFA),该方法通过每个分割时间序列区间上波动的平均值作为统计点,根据波动函数的幂律性确定广义Hurst指数,对平稳和非平稳序列结构及波动奇异性进行度量,被证明是检验噪声序列和非平稳时间序列是否具有多重分形特征的有效方法。
基于分形、分形理论和分形市场的研究已经广泛应用于股票期货市场,可以有效地判断市场的趋势,预测价格、成交量和交易时机[6]。目前对于分形的研究方法主要有分整自回归移动平均模型(ARFIMA)、重标极差分析(R/S)、修正R/S方法、消除趋势波动分析方法(DFA)和多重分形消除趋势波动分析法(MFDFA)。
重标极差分析为识别金融市场价格行为及定价的有效性问题提供了一个非线性工具,从而不必依赖独立性假设和正态分布来考察价格行为。重标极差分析可以确定金融市场价格时间序列中最重要的两个重要信息,即H指数和平均记忆长度,从而揭示了金融市场价格行为的持久性和长期记忆性的特征[7]。时间序列的持久性和长期记忆性显示了金融市场价格运动中的非线性关系,证明了市场的无效性,可以为投资决策提供重要参考。
二 重标极差分析
重标极差分析是1951年由H.E.Hurst提出的,主要计算过程如下:将原时间序列分成各个元素邻接的A个长度为N的子序列,计算各个子序列平均的R/S(累积离差的极差/标准差)指标值,并记录相应的数据容量N。持续这个过程直到子序列的样本容量为A×N/2为止,得到一系列的R/S-N数值对。用V统计量估计长期记忆期的平均循环长度[8]。V统计量表示为式(1)

(1)
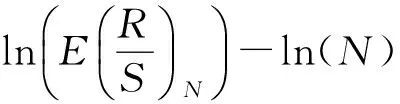
(一)计算重标极差(R/S)
设一个时间序列Pt,观测次数为m,将其转换为长度为M=m-1的常用对数比率时间序列:Xt=lnPt-ln
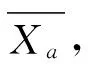
(2)
(3)
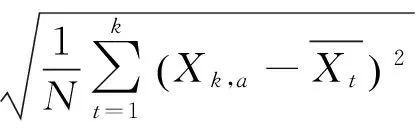
(4)
(5)
式(1)~(4)中;
N为子区间Ia的长度。
Dk,a为子区间Ia的累积离差。
RI,a为子区间的极差。
SI,a为第a个区间Ia的标准差。

(二)估计平均循环长度
平均循环长度的计算公式为式(6):

(6)
(三)计算Hurst指数
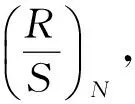
(7)
(四)计算R/S和H指数的期望值
对于序列R/S指标期望值的估计,使用Peters提出的计算R/S期望值的公式,即式(8):
(8)

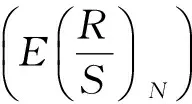
(9)
三 数据处理
由于两种有色金属期货合约具有一定的时间跨度,选取每个交易日的主力期货合约连续数据进行分析。十二五期间,我国期货市场蓬勃发展,两种有色金属期货品种交易活跃。选取上海期货交易所有色金属中的沪铜和沪铝两个期货品种进行分析,由于在重标极差分析中,要尽量选取有最多公因子的时间序列,所以选取的沪铜期货品种的时间范围为2011年1月4日到2015年12月16日,沪铝期货品种的时间范围为2011年1月4日到2015年12月14日。选取两种有色金属期货品种的收盘价进行对数一阶差分计算期货价格的收益率:Xt=lnPt-lnPt-1。
使用Eviews做描述性统计,特征如表1所示。

表1 有色金属期货价格收益率描述性统计特征
从表1中可以看出,沪铜和沪铝期货都为左偏,并且峰度都大于3,两个期货品种的收益率都表现了非常明显的尖峰厚尾的特征。从JB正态检验中可以看出两者都不服从正态分布。
沪铜和沪铝的时序图如图1、2所示。

图1 沪铜期货收益率时序图

图2 沪铝期货收益率时序图
从图1、图2可以看出,我国有色金属期货价格收益率的波动均存在明显的波动集聚性,但沪铜期货相比沪铝期货,收益率的波动集聚性更加明显,波动异常值明显偏少。
沪铜期货和沪铝期货收益率的分布直方图如图3、图4所示。
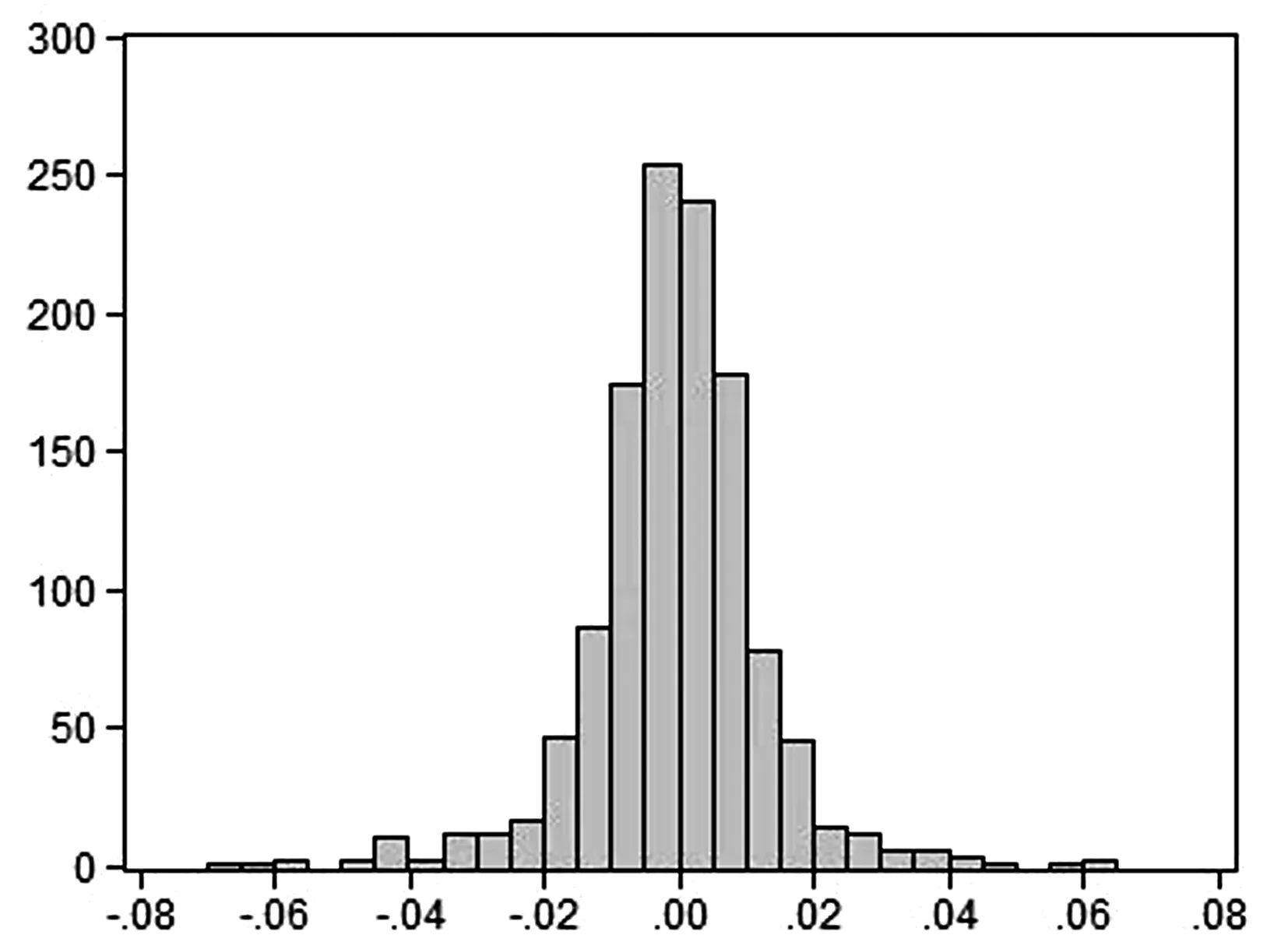
图3 沪铜期货收益率分布直方图

图4 沪铝期货收益率分布直方图
从图3、图4可以看出,我国有色金属期货价格收益率总体保持平稳,没有明显的左偏或右偏分布。
四 实证分析
选取2011年1月4日到2015年12月16日的沪铜期货品种数据和2011年1月4日到2015年12月14日的沪铝期货品种数据。使用matlab软件编程进行计算,判断两种有色金属期货品种的价格行为是否具有分形特征,是否具有持久性和长期记忆性的特点,通过计算V统计量产生变化的时点,得到长期记忆周期。沪铜和沪铝期货的V统计量变化如图5、图6所示。

图5 沪铜期货的V统计量
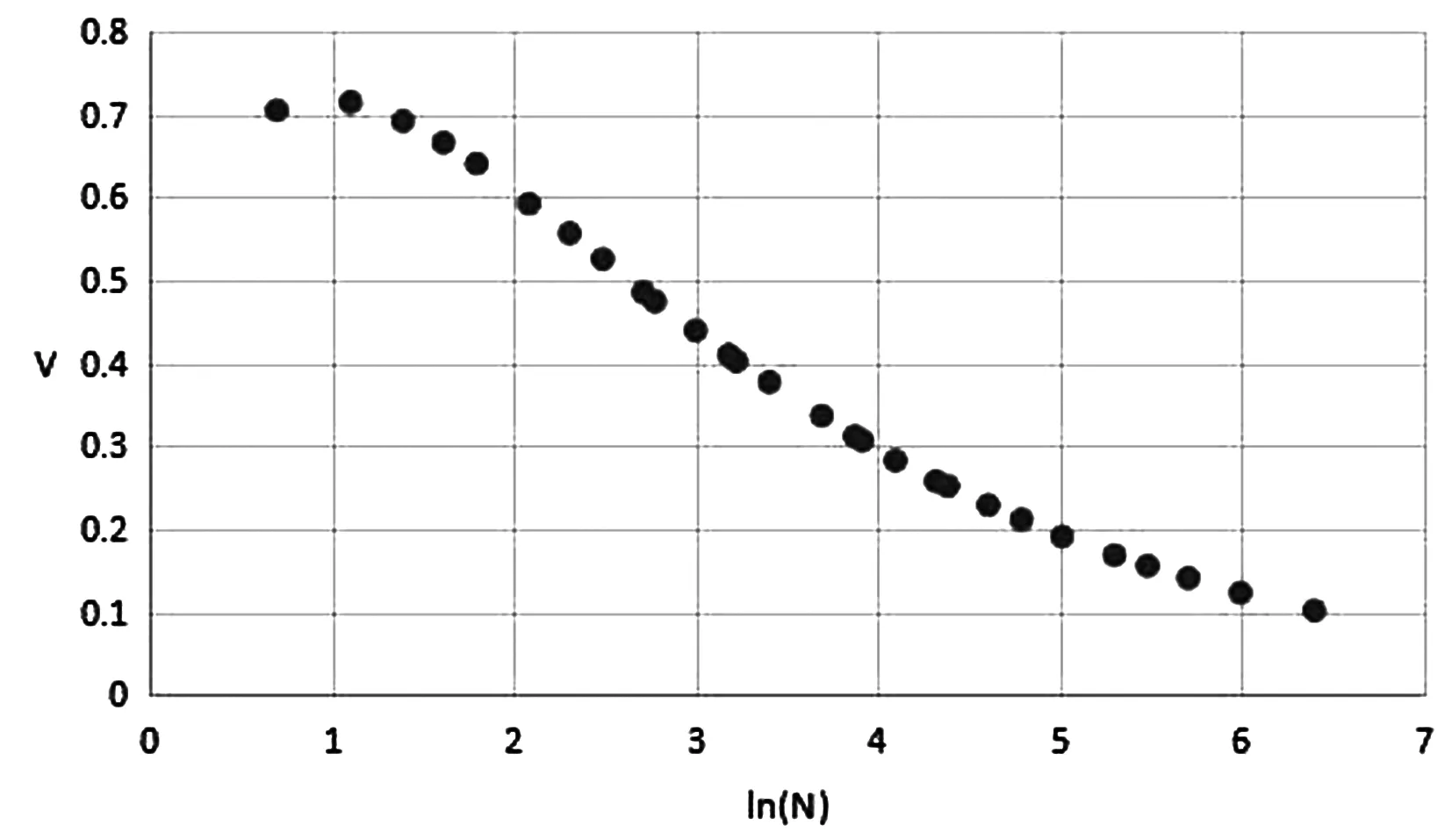
图6 沪铝期货的V统计量
从图5、图6可以发现沪铜和沪铝两种有色金属期货品种经历了不同的V统计量变化,在不同的时点出现了逆转。从两种有色金属期货品种V统计量转折处发现,两种有色金属期货品种具有不同的长期记忆周期,反映了系统的平均循环天数。其中沪铜期货的平均循环天数为545天,沪铝期货的平均循环天数为572天。两种有色金属期货品种的不同长期记忆周期是由于各自的期货品种的特点和市场环境造成的。沪铝期货比沪铜期货的平均循环天数更长,即具有更长的长期记忆周期,长期记忆特征更为明显。
在价格行为的长期记忆消失之前,对V统计量出现逆转前的R/S指标对数期望数据与时间序列的样本容量的对数数据进行对数回归,对数回归的斜率为H值,结果如图7、图8所示。

图7 沪铜期货的R/S对数回归
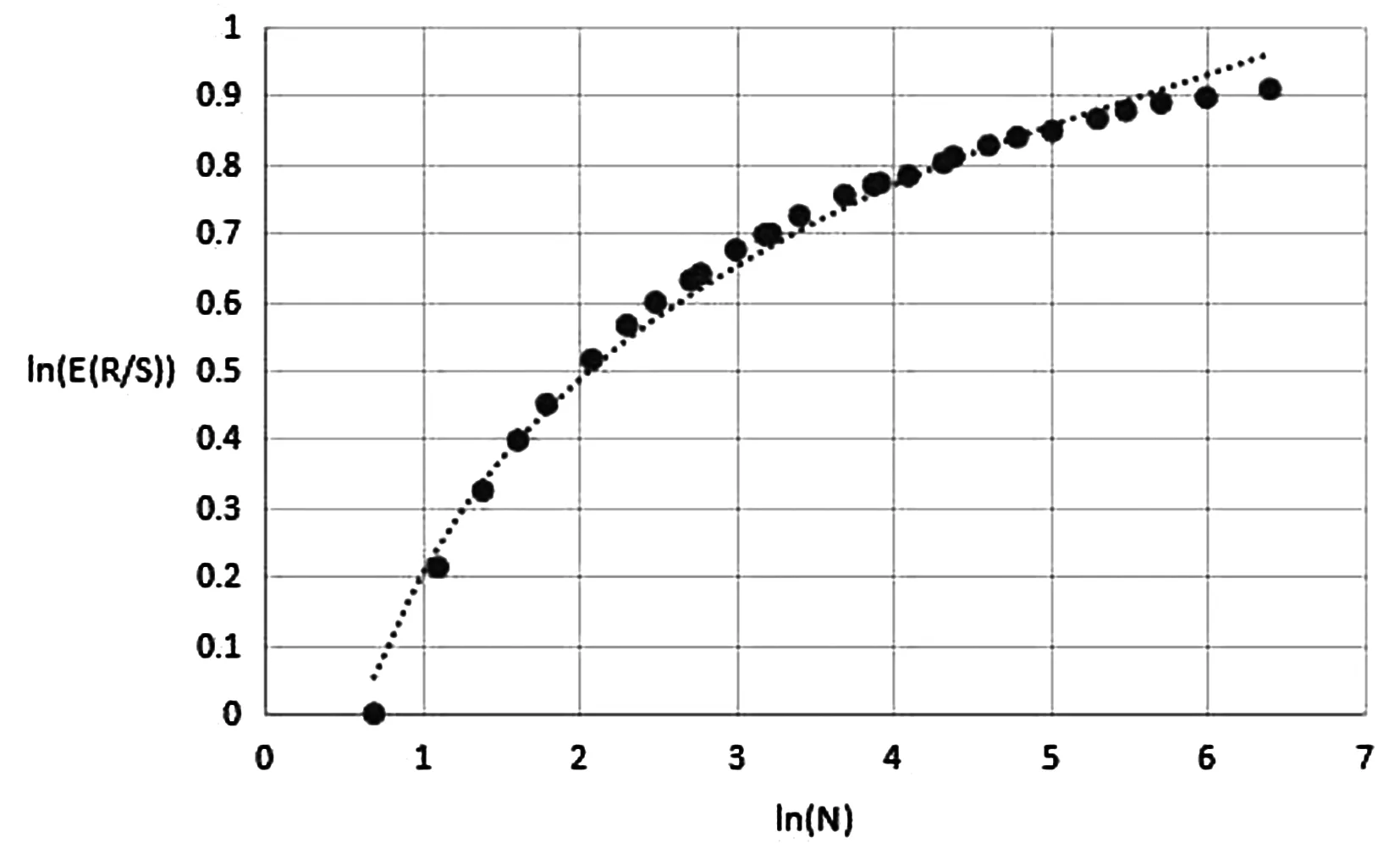
图8 沪铝期货的R/S对数回归
沪铜期货的对数回归方程为
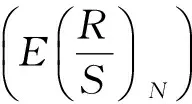
R2=0.980
沪铝期货的对数回归方程为
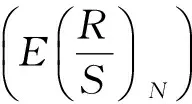
R2=0.989
从图7、图8可以看出沪铜和沪铝期货的R/S指标对数期望数据与时间序列的样本容量的对数数据符合对数回归,拟合程度较高,R2达到了0.98,沪铜期货的对数回归方程的R2为0.980,沪铝期货的对数回归方程的R2为0.989,沪铝期货的拟合程度更好一些。对数回归方程的斜率就是H值,沪铜期货对数回归方程的斜率,即沪铜期货的H值为0.389,沪铝期货对数方程的斜率,即沪铝期货的H值为0.408,两者都小于0.5,显示反持久性的特点。表明有色金属期货市场价格具有反持久性的特点,是一个有偏的随机游走过程,尚未达到弱式有效。在沪铜和沪铝两种期货品种中,沪铜的H值比沪铝低,沪铜期货反持久性的特点更加明显。
两种有色金属期货品种重标极差分析的平均循环天数和H指数如表2所示。

表2 有色金属期货的循环天数和H值
从表2中可以看出,沪铜期货的平均循环天数为545天,沪铝期货的平均循环天数为572天,沪铝期货比沪铜期货的平均循环天数更长,即具有更长的长期记忆周期,长期记忆特征更为明显。沪铜期货的H指数为0.389,沪铝期货的H指数为0.408,在沪铜和沪铝两种期货品种中,沪铜的H值比沪铝低,沪铜期货反持久性的特点更加明显。
五 主要结论
选取2011年1月4日到2015年12月16日的沪铜期货品种数据和2011年1月4日到2015年12月14日的沪铝期货品种数据进行重标极差分析计算,发现如下结论:
(1)有色金属期货市场价格H值均小于0.5,即具有反持久性的特点,是一个有偏的随机游走过程,尚未达到弱式有效。两种有色金属期货品种的反持久性不同,其中沪铜期货的H值为0.389,沪铝期货的H值为0.408。由此可见,在两种期货品种中,沪铜的H值比沪铝低,沪铜期货反持久性的特点更加明显。可以利用反持久性分析有色金属期货时间序列的特征,做好投资决策。
(2)两种有色金属期货品种V统计量变化的不同与各自期货价格的变动趋势有关。最后两种有色金属期货品种的V统计量都发生了转折,但具体时点又有所不同。从两种有色金属期货品种V统计量转折处发现,两种有色金属期货品种具有不同的长期记忆周期,反映了系统的平均循环长度。其中沪铜期货的平均循环天数为545天,沪铝期货的平均循环天数为572天。两种有色金属期货品种的不同长期记忆周期是由于各自的期货品种的特点和市场环境造成的。利用期货长期记忆周期可以有效分析有色金属期货价格时间序列的特征,为投资决策提供参考。
(3)沪铜和沪铝期货的价格收益率时间序列都呈现非线性特征。市场对信息的反应行为最终表现在期货价格上,使得期货价格所构成的时间序列呈现出非常明显的非线性特征。
(4)有色金属期货市场呈现了明显的波动集聚性,市场具有一定风险,价格连续暴涨暴跌,在某些时段,价格大幅波动,上下浮动明显,但在另外一些时段,价格小幅波动,上下并不明显,市场呈现平稳态势。投资者需要对期货市场做出准确判断才可以在这个复杂的市场中获益。
[1] Richards G R.A fractal forecasting model for financial time series[J].Journal of Forecasting,2004,23(8):586-601.
[2] Masteika S,Rutkauskas A V,Lopata A.Chaos and Complex Systems[M].Springer Berlin Heidelberg,2013:295-299.
[3] Peters E.Fractal Market Analysis: Applying Chaos Theory to Investment and Economics[M].John Wiley & Sons,Inc.,1994: 28-30.
[4] Peng,C K,Buldyrev S V,Havlin,S.Mosaic organization of DNA nucleotides[J].Physical Review E ,1994,49(2):1685-1689.
[5] Kantelhardt J W,Zschiegner S A,Koscienlny-Bunde E,et al.Multifractal detrended fluctuation analysis of nonstationary time series[J].Physica A ,2002,316(1-4):87-114.
[6] Xianming W,Xianjun Z,Mi Z.Nonlinear Concept,Fractal Theory and Futures Zinc Markets Prices[J].The Theory and Practice of Finance and Economics,2011.
[7] Yi I G,Kim B J.Fractal Profit Landscape of the Stock Market[J].PLoS ONE,2012.
[8] 苑莹,庄新田,金秀.期货价格收益序列的多重分形统计描述及成因分析 [J].东北大学学报(自然科学版),2010,31(4): 605-608.
ResearchonFractalCharacteristicsofNonferrousMetalFuturesMarkets
LINJie,GONGZheng
(SchoolofEconomicsandManagement,TongjiUniversity,Shanghai200092,China)
Through rescaled range analysis method,using the "Twelfth Five-Year Plan" period of market transaction data,the fractal characteristics of Shanghai copper and aluminum two non-ferrous metals futures is on empirical research,then results show that,two non-ferrous metal futures price returns time series are volatility clustering and nonlinear,and has the fractal characteristics of anti-persistence and long-term memory,and is a biased random walk process.Two kinds of nonferrous metals futures have different long-term memory cycles,which are 545 days and 572 days respectively,reflecting the average cycle length,and H index is 0.389 and 0.408 respectively,indicating that China's non-ferrous metals futures market has not reached the weak form efficiency.
Nonferrous Metal Futures;Rescaled Range Analysis;Fractal Characteristics;Anti-Persistence;Long-Term Memory
2016-12-28
国家自然科学基金资助项目(71071114,71672128);上海市重点学科建设基金资助项目(B310);同济大学中央高校基本科研业务费资助项目。
林杰(1967—),男,四川渠县人,同济大学经济与管理学院教授,博士生导师,研究方向:期货程序化交易;决策支持系统;供应链管理。
F
A
1008—1763(2017)03—0080—05

