直线舵机测试台系统建模与仿真

胡新宇， 张 东， 刘 音， 张道德

(1 湖北工业大学机械工程学院， 湖北 武汉 430068; 2 武汉市轻工装备工程技术研究中心， 湖北 武汉 430068)

直线舵机测试台系统建模与仿真

胡新宇1,2， 张 东1,2， 刘 音1，2， 张道德1,2

(1 湖北工业大学机械工程学院， 湖北 武汉 430068; 2 武汉市轻工装备工程技术研究中心， 湖北 武汉 430068)

分析直线舵机测试台机械结构，通过数学公式推导，以及直线电机、舵机和机械连接部分建模，给出模拟加载信号对系统模块的运行仿真，就测试台系统普遍存在的静态负载力震荡和动态加载多余力问题进行研究，应用内、外双环控制与利用系统结构不变形原理进行多余力补偿的复合控制。根据实际元器件型号规格，确定仿真模块中各参数数值，通过系统模型在Simulink软件下的仿真数据结果对比分析，得出复合控制策略提高系统性能、满足测试台系统加载精度要求的结论。

直线舵机； 系统建模； 复合控制策略； Simulink仿真

舵机测试台系统设计方法目前主要存在舵机高频运动时对测试台强位置干扰产生的系统稳定性和多余力抑制[1]问题，导致整个测试台系统在仿真时舵机运动对测试台负反馈与实际测试情况存在误差。为获得与实际测试情况更为接近的仿真数据，本文采用加载机构与被加载机构单独建模，实现干扰的实时变化，同时实验室能完成模拟直线舵机在实际工作中收到多种形式的稳定负载力(如阶跃负载，正旋负载和线性负载等)；运用结构不变性原理[2]对加载过程中随着直线舵机运动系统的静态加载稳定性和动态加载多余力的抑制中的难点问题进行研究。

1 机构建模

1.1 系统机械结构

本系统加载机构与被加载机构之间通过力传感器进行刚性连接。电机动子部分固定于直线导轨滑块上，由直线电机驱动工作台沿直线导轨做直线运动，动子与传感器、传感器与舵机运动轴刚性连接，直线电机做直线运动产生的直线力通过力传感器传递到舵机运动轴，从而实现舵机运动下负载力模拟。

1.2 系统数学建模

加载机构主要作用是产生多种类型加载力。选用永磁无刷同步直线电机，采用d-q坐标变换[3]进行研究。

在d-q同步坐标系下永磁直线电机电压方程为：

电机直线速度

交轴电压平衡方程：

(1)

动子运动力平衡方程：

(2)

式中：Rs为动子绕组电阻，φd为d轴电机绕组磁链，Pn为极对数，τ为极距。F为电机电磁推力，m为动子质量，x为动子位移，Fd为负载力，B为系统阻尼，Kf为电机推力系数。

由式(1)-(4)得到电机模型如图1所示。

由图1可以得到直线电机的开环数学模型：

(3)

直线电机开环传递函数：

(4)

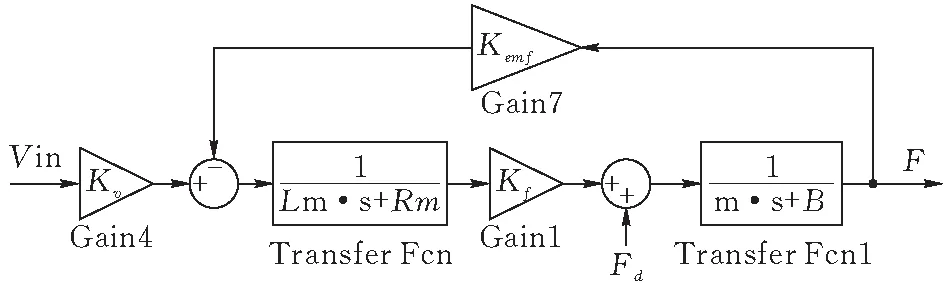
图 1 直线电机数学模型

负载机构指被负载力加载的直线舵机。本测试台选取的为电动式直线舵机，主要由伺服控制器、直流伺服电机、减速器、位置反馈电位计和减速齿条构成[4]。

系统结构原理如图2所示。

图 2 直线舵机系统结构原理图

误差信号方程：

ei=Ui-Uf

伺服放大方程：

Ui=Kei

电枢回路电压平衡方程：

反电动势方程：

舵机轴力平衡方程：

F=Cfi

舵机输出轴位移

式中：ei为误差信号，Ui为输入信号，Uf为反馈信号，K为伺服放大系数，Ui伺服输出信号。Lx为舵机电枢绕组电感，i为电枢绕组电流，Ex为反电动势，Ck为反电动势系数，S为舵机输出轴位移，M为舵机输出轴质量，f为舵机与负载折合到舵机输出轴上的摩擦系数，F为舵机输出力，Fd为负载力，Cf为舵机输出力系数，N为减速系数。

舵机系统结构如图3所示。

图 3 直线舵机系统结构图

2 系统控制策略分析

基于伺服电力控制特点，采用双环与多余力补偿的复合控制策略[5]。所谓复合控制策略，即外环采用力环，内环采用电流环，外部同时进行多余力补偿控制。这种复合控制策略能抑制加载过程中力变化引起的电机内控制电流的强耦合而产生的互相干扰，从而使控制过程中电机实际输出力更加接近目标输出力，控制效果更优。

静态负载力震荡主要是在力闭环控制器作用下，输出力接近指令力时，直线电机控制器控制输出电压Vout接近输入指令电压Vin，力闭环控制器就会给控制电压Va一个较小的值，交轴电流Iq减小，导致电磁推力F减小，输出力减小，导致原本逼近指令力的曲线又远离，力误差加大，此时在控制器的作用下，又会加大控制电压Va，如此反复，闭环作用下电机输出力则出现抖动震荡。图4为直线电机系统结构图，图5为Simulink仿真结果图。

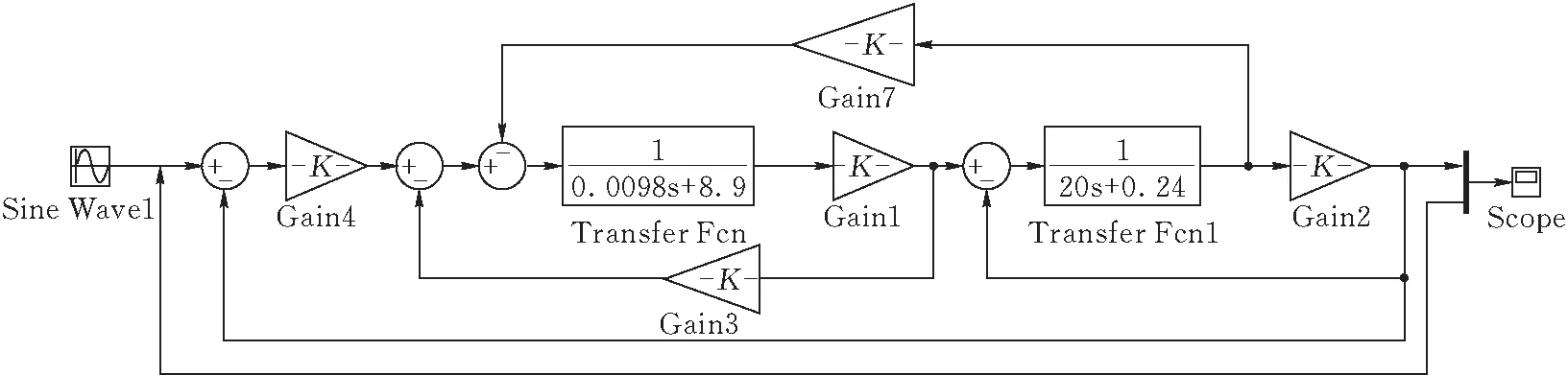
图 4 直线电机系统结构图

从图2中得到的仿真结果可见，当输入力为幅值100N、频率为10Hz正旋信号时，输出力最大值只能达到95.6N，稳态误差达到4.4%，且波峰波谷力换向处有震荡。结合多次仿真数据可以分析系统误差较大以及产生震荡的原因：在输出力接近峰值时，由于力闭环控制器的伺服控制特性，输出力始终不能达到误差允许范围内数值，同时系统跟随性也不能达到最优，系统有一定的滞后。系统稳态误差4.4%，大于最大允许误差1%，系统不能达到技术指标要求。

为减小稳态误差和震荡，提高系统性能，在电机输出力后取积分再引入微分力反馈，能够对输出力的趋势进行预测，加强舵机运动对电机输出力的干扰反馈，使输出力最大值能够更加接近峰值，加快系统响应速度，同时在系统加入PID控制[6]，以减小系统稳态误差和震荡，达到优化控制目的。

优化后直线电机系统结构如图6所示。频谱特性曲线如图7所示。

图 6 优化后直线电机系统结构

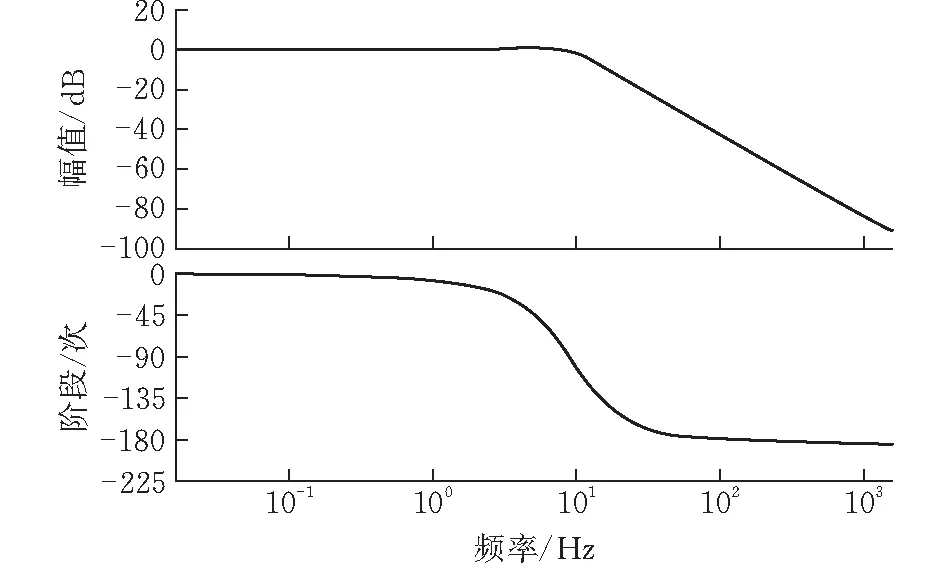
图 7 直线电机系统频谱特性曲线

由图7可得，直线电机仿真频率在小于10Hz时，相位滞后较小，可满足技术指标要求，在仿真加载最大频宽10Hz时，系统相位滞后103°，幅值衰减1.93dB，系统幅频特性理想。优化效果明显。

动态加载多余力是模拟加载器中普遍存在的问题，也是制约加载器精度的关键因素。多余力的产生是由于直线电机加载时动子运动速度与直线舵机输出轴运动速度不同步导致的，所以多余力在实际中不能完全消除，只能抑制其大小。

利用结构不变性原理，采用速度反馈补偿方法[7]，在舵机运动过程中对直线电机产生强位置干扰，两者之间存在速度差，测量反馈舵机输出轴速度，对直线电机动子进行速度补偿，将速度补偿信号反馈到加载机构伺服控制中，从而实现直线电机动子与舵机输出轴速度同步，达到抑制多余力效果。

设置加载机构力指令为零，舵机以频率5Hz、幅值5mm作正旋运动，系统多余力测试如图8所示。由图8，可以得到此时系统多余力为3.2N，因篇幅有限，直接给出相同条件不同频率下多余力数值：1Hz时，多余力为2.5N;2Hz时，多余力为2.6N；3Hz时，多余力2.8N;4Hz时，多余力3.1N。

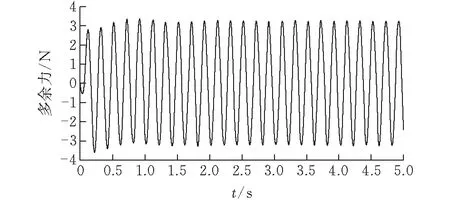
图 8 系统多余力测试图

根据多次仿真数据可以得出：在舵机以频率5Hz、幅值5mm高频运动时，通过系统复合策略控制，系统多余力仅为3.2N，且当舵机运动频率越小时，多余力相应越小，该控制方法滞后小，具有超前性，能较好抑制多余力，工程实现较为可行，能实现速度同步控制，满足控制要求。

3 系统仿真

整个直线舵机测试台系统在Simulink环境下建立仿真模型(图9)。

图 9 Simulink下测试台系统仿真结构图

根据实际直线电机所选型号，部分仿真参数选取如下：直线电机伺服控制器放大KV= 5.75；电枢绕组电感Lm=0.0098 H；电枢等效电阻Rm= 6.9 Ω；动子与连接处总质量m=20 kg；测试台等效阻尼B=0.24；电磁推力系数Kf=118 N/A；力传感器传递系数K=1000；反电动势系数KEMP=100；舵机电枢绕组电感Lx=0.003 H电枢绕组电阻与伺服放大器等效电阻R=1 Ω，反电动势系数Ck= 0.7，舵机输出轴质量M=0.8 kg， 舵机输出力系数Cf=4；减速系数N=0.08。PID参数Kp=1.5，Ki=1.5，Kd=1.5。

通过图10，可得整个测试台系统频宽在10 Hz左右。在小于10 Hz频宽时，相位滞后较小，可满足技术指标要求频宽；在频宽10 Hz时，相位滞后92.5°，但幅值衰减2.05 dB，幅频特性较为理想。

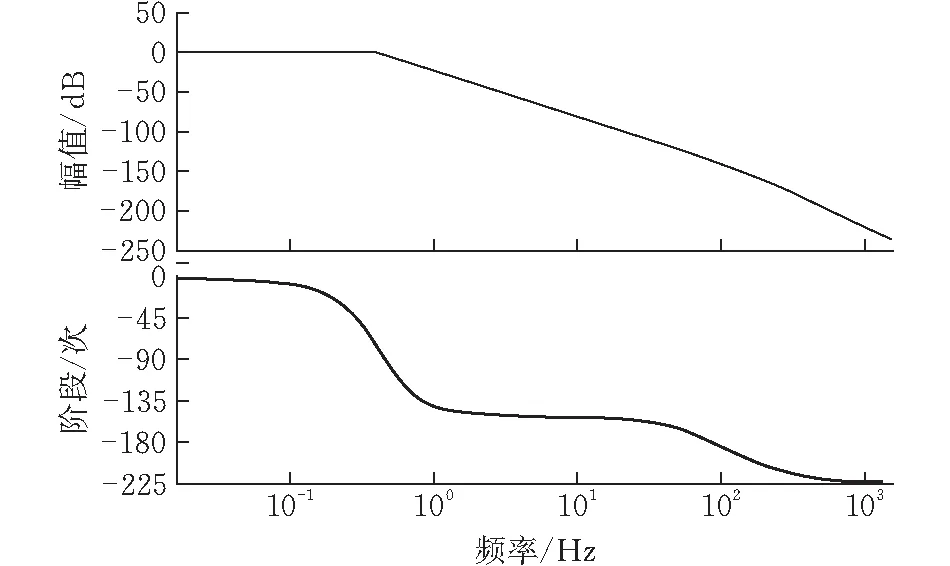
图10 测试台系统仿真Bode图

图11为测试台系统在Simulink下的仿真结果，舵机运动为幅值10 mm、频率1 Hz正弦运动，加载力指令为幅值100 N、从左至右依次为1 Hz、3 Hz、5 Hz、7 Hz，加载时间5 s。分析仿真结果，加载频率越大加载误差越大，最大加载误差在7 Hz时为3.5%，系统有延时0.02 s，系统性能能满足技术指标要求。

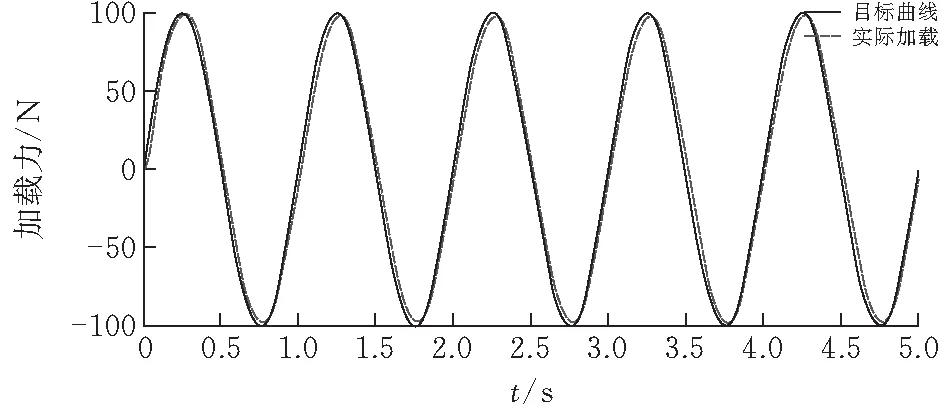
(a)1 Hz

(b)3 Hz

(c)5 Hz

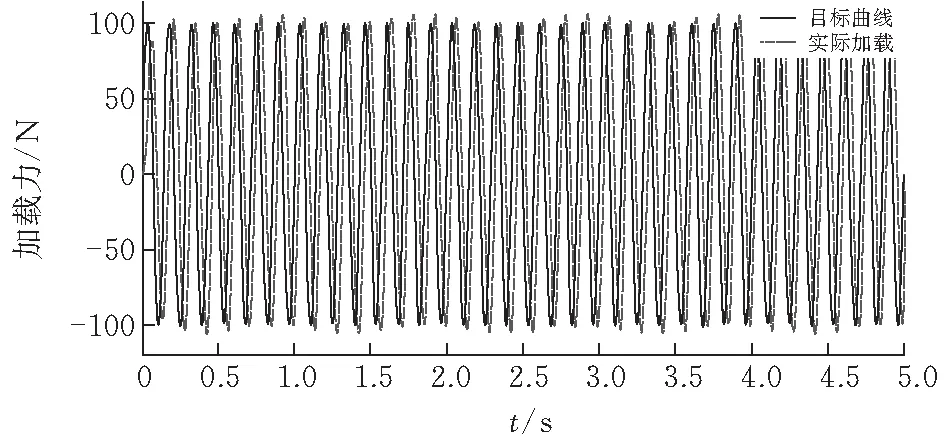
(d)7 Hz图11 Simulink下测试台系统仿真结果

4 结论

1)舵机运动下的强位置干扰能通过电机输出力取积分再引入微分力进行反馈补偿。

2)舵机正弦运动频率越低，多余力抑制效果越好，实际工作时舵机频宽应不超过10 Hz。

3)采用内外双环与多余力补偿的复合控制策略能够很好地抑制多余力和提高系统稳定性。

[1] 王成, 王广怀. 负载模拟器多余力抑制的探讨[J]. 机械工程师, 2003(12):38-40.

[2] 范金华．航弹舵机加载测试系统研究[D]．长沙：国防科学技术大学，2005.

[3] 陶果, 邱阿瑞, 李大雷. 横向磁场永磁同步电动机d-q轴模型研究[J]. 微电机, 2008, 41(2):8-10.

[4] 鲍传美, 陈刚, 李云. 基于Matlab/Simulink的电动舵机系统建模与仿真[C]// 2006企业产品国际化战略与微电机技术发展论坛， 2006.

[5] 夏长亮, 李志强, 王迎发. 无刷直流电机小脑模型网络与PID复合控制[J]. 电机与控制学报, 2008, 12(3):254-259.

[6] 吴宏鑫, 沈少萍. PID控制的应用与理论依据[J]. 控制工程, 2003, 10(1):37-42.

[7] 潘超, 左健民, 汪木兰. 基于前馈及反馈补偿的高性能直线伺服系统[J]. 系统仿真学报, 2010(12):3025-3029.

[责任编校： 张 众]

Linear Servo System Modeling and Simulation Test Bench

HU Xinyu1，2, ZHANG Dong1，2, LIU Yin1,2, ZHANG Daode1,2

(1SchoolofMechanicalEngin.，HubeiUniv.ofTech.，Wuhan430068，China; 2Engin.RearchCenterofWuhanLightIndustyEquipment,Wuhan430068,China)

In this paper, the static load vibration force and dynamic loading extraneous force of the loading station system are studied through the analysis of the linear servo test mathematical derivation, system modeling and simulation of content. It also uses the inner and outer loop control and utilization system structure, deformation theory in the composite control strategy of the extraneous force compensation. According to the actual device selection of parameters and after the system model in Simulink software simulation data are compared with the results of analysis, the conclusion is drawn that the compound control strategy can improve the system performance,and the loading platform system meets the requirement of the loading precision.

linear actuator；system modeling；compound control strategy；simulink simulation

2017-01-13

湖北省教育厅重点资助项目(Di0151406)

胡新宇(1976-)， 男， 湖北黄冈人，工学博士，湖北工业大学教授，研究方向为图像处理，智能控制及机电设备

张 东(1989-),男，湖北黄冈人，湖北工业大学硕士研究生，研究方向为智能控制及机电设备

1003-4684(2017)02-0007-05

TP391.9

A