具有柔性维护周期的单机误工排序问题

李 丹，张 安，陈 永，陈光亭

(杭州电子科技大学理学院，浙江 杭州 310018)

具有柔性维护周期的单机误工排序问题

李 丹，张 安，陈 永，陈光亭

(杭州电子科技大学理学院，浙江 杭州 310018)

主要研究了具有柔性维护周期的单机误工排序问题.首先证明了极小化误工工件数目标是不可近似的，即不存在具有常数界的多项式时间近似算法，接着设计了求解问题的伪多项式时间动态规划算法.

排序；误工工件；柔性维护周期；动态规划

0 引 言

现代工业生产中，为提高机器的工作效率或防止机器因持续运行而发生故障，一种常见的策略就是对机器进行定期维护[1].学者们主要研究了机器具有固定维护周期(Periodic Maintenance，PM)的单机排序问题.当目标函数为极小化误工工件数时，文献[2]利用分支定界法获得最优解，并在Moore算法基础上设计了启发式算法，数值实验表明该启发式算法是有效的.文献[3]给出了混合整数规划模型，并提出了一个改进启发式算法，通过数值实验说明改进启发式算法要比文献[2]中的启发式算法更为有效.文献[4]给出了两个伪多项式时间动态规划算法和一个完全多项式时间近似方案，并通过大量数值实验验证了提出的算法是有效的.文献[5]为了改进现有水平的精确算法，基于有效的下界程序和若干新的主要性质，提出了新的分支定界算法，数值实验表明该精确算法是有效的.与上述文献不同，本文主要研究具有柔性维护周期(Flexible Periodic Maintenance，FPM)的单机误工排序问题.

1 问题陈述及符号说明

图1 固定维护周期(PM)

图2 柔性维护周期(FPM)

2 不可近似性证明与动态规划算法

2.1 问题P1的不可近似性

通过多项式时间归约法来证明排序问题P1是不可近似的，即不存在具有常数界的多项式时间近似算法.

构造排序问题P1的一个实例I′：n个工件J1，…，Jn，工件的加工时间pj=aj(称为整数aj对应的工件)，工期dj=d=2T+N，1≤j≤n,机器的维护周期为T，每次维护的时长为N.令F*表示排序问题P1的实例I′的最优值.

引理1 若划分问题实例I的答案为“是”，则对应排序实例I′的最优值F*=0.

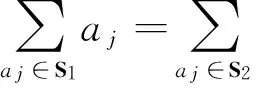
引理2 若划分问题实例I的答案为“否”，则对应排序实例I′的最优值F*≥1.

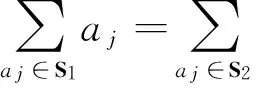
定理1 对任意r≥1，排序问题P1不存在最坏情况界为r的多项式时间近似算法.

证明 反证法.假设P1存在最坏情况界为r的多项式时间近似算法A，则对任意划分问题的实例I，首先在多项式时间内构造排序问题P1的实例I′，接着调用P1的多项式时间算法A，根据算法A的目标值FA的情况：

情形1FA≤0.由0≤F*≤FA≤0可得F*=0.由引理1和引理2，划分问题实例I的答案为“是”.

综上，算法A可以用来求解划分问题.因为从划分问题的实例构造排序问题实例的过程和算法A都是多项式时间的，所以划分问题就存在多项式时间的最优算法，即证明了划分问题属于P类问题，这与划分问题属于NP-完全类问题矛盾(除非P=NP).故P1不存在最坏情况界为r的多项式时间近似算法.证毕.

2.2 问题P1的动态规划与可解情形

本节给出求解问题P1的动态规划算法.不失一般性，假设工件工期满足d1≤d2≤…≤dn,即最早交工期优先(Earliest Due Date First,EDD)，且不妨假定任一合理排序由两部分组成：不误工工件按EDD序排在前面加工；误工工件以任意顺序排在后面加工.

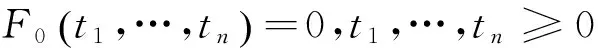
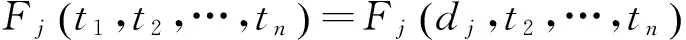
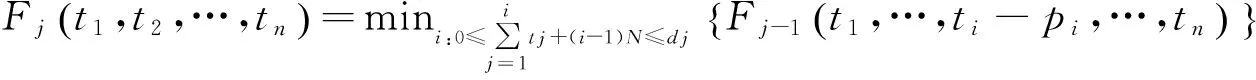
(1)

3 结束语

本文研究了具有柔性维护周期的极小化误工工件数的单机排序问题，证明了该问题是不可近似的，并给出了该问题的动态规划算法.下一步将在柔性维护周期条件下，研究加工与运输协同的一体化运输排序等问题.

[1]ARTSR,KNAPPGM,MANNJRL.Someaspectsofmeasuringmaintenanceperformanceintheprocessindustry[J].JournalofQualityinMaintenanceEngineering, 1998,4(1):6-11.

[2]CHENWJ.Minimizingnumberoftardyjobsonasinglemachinesubjecttoperiodicmaintenance[J].Omega, 2009,37(3):591-599.

[3]LEEJY,KIMYD.Minimizingthenumberoftardyjobsinasingle-machineschedulingproblemwithperiodicmaintenance[J].Computers&OperationsResearch, 2012,39(9):2196-2205.

[4]YINY,XUJ,CHENGTCE,etal.Approximationschemesforsingle-machineschedulingwithafixedmaintenanceactivitytominimizethetotalamountoflatework[J].NavalResearchLogistics(NRL), 2016,63(2):172-183.

[5]LIUM,WANGS,CHUC,etal.Animprovedexactalgorithmforsingle-machineschedulingtominimisethenumberoftardyjobswithperiodicmaintenance[J].InternationalJournalofProductionResearch, 2016,54(12):3591-3602.

Minimizing the Number of Tardy Jobs on a Single Machine with Flexible Periodic Maintenance

LI Dan, ZHANG An, CHEN Yong, CHEN Guangting

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

This paper studies the problem of scheduling jobs on a single machine that requires flexible periodic maintenance. The objective is to minimize the number of tardy jobs. it proves that the problem cannot be approximated within a constant worst case ratio. Then a pseudo-polynomial time dynamic programming algorithm is proposed.

scheduling; tardy jobs; flexible periodic maintenance; dynamic programming

10.13954/j.cnki.hdu.2017.03.017

2016-12-01

国家自然科学基金资助项目(11571252，11401149)；浙江省自然科学基金资助项目(LY16A010015)

李丹(1991-)，女，甘肃兰州人，硕士研究生，组合优化.通信作者：陈光亭教授，E-mail：gtchen@hdu.edu.cn.

O221.7

A

1001-9146(2017)03-0084-03