供水管网水质监测传感器网络布局优化

沈一凡，魏冠雄，侯迪波，黄平捷，张光新,张宏建

(浙江大学控制科学与工程学院,浙江 杭州 310027)

供水管网水质监测传感器网络布局优化

沈一凡，魏冠雄，侯迪波，黄平捷，张光新,张宏建

(浙江大学控制科学与工程学院,浙江 杭州 310027)

为应对突发污染物注入预防供水管网的问题，水质监测传感器网络布局优化已越来越多地受到研究关注。针对基于“服务水平”概念的布局优化模型易受主观因素干扰的问题，提出了污染事件检测时间最短模型。该模型以污染事件平均检测时间为优化目标，无需人为设定“服务水平”，所得布局方案监测点数量完全由预算决定。一旦给定监测点数量，能够保证污染事件平均检测时间最优，充分保证了模型的客观准确性。对供水管网系统状态进行了平均化处理，提高了计算资源的空间利用率。同时，针对目前常用的模型参数寻优算法难以满足大规模供水管网模型求解的特点，提出了基于多线程机制的并行粒子群优化(PSO)算法，从而充分发挥多核心处理器的计算能力，提高了硬件资源的利用率，加快了模型计算的速度。试验结果表明，所提出的模型和优化算法对实际的供水管网水质监测网络布局优化选址具有一定的参考作用。

供水管网； 水污染； 水质监测网络； 并行粒子群算法； 节点优化布局； 时间最短模型； 多线程； 拓扑结构

0 引言

近年来，供水管网中突发污染物注入已成为各国政府重点防范的供水管网系统水污染来源[1-2]，造成了严重的危害和损失。在每个节点设置监测仪器成本巨大，不切合实际，因此需要优化监测网络布局。

针对此类问题，Kumar等[3-4]首先提出了“q体积服务水平”的概念。“q体积服务水平”即从污染物开始注入，到第一次检测到有污染物注入的这段时间内，供水管网系统已经对外供出的污染水体积。Ostfeld等[5]提出了一个混合整数规划模型，以求解供水管网水质监测传感器网络布局优化问题。Berry等[6]则以受污染水影响的人口数量最少为目标，建立了一个混合整数规划模型并对其进行求解。显然，此类问题的模型应尽量避免引入主观因素，保持模型的客观正确性；同时，随着管网系统规模的日益增大，模型应能够满足不同需求下的供水管网水质监测传感器网络布局优化研究，求解算法应具备较好的时效性和存储空间利用率。

为了克服基于“服务水平”概念的模型易受主观因素干扰、一般寻优算法难以满足大规模供水管网模型求解的缺点，提出了污染事件检测时间最短模型。本模型以污染事件平均检测时间最短为目标，对供水管网系统状态进行了平均化处理，并利用基于多线程机制的并行粒子群优化(particle swarm optimization,PSO)算法优化求解问题模型，提升了模型求解的效率。

1 污染事件检测时间最短模型

1.1 假设条件

管网系统本身具有较高的动态变化特性，同时污染事件具有较大的不确定性；基于突发污染物注入事件模拟的供水管网水质监测传感器网络布局优化问题，以随机污染矩阵的方式模拟污染物注入事件，未必能够将所有情况计算在内。因此，在构建模型之前，对管网系统本身作了一定的简化，主要包括以下几点。

①突发污染物注入事件可在任意节点发生，且每个节点发生污染物注入事件的概率相等。同时，在本模型中，只考虑单污染源形式，即任意时刻只有一个节点发生突发污染事件。

②污染物在管网中以一维平流输送的形式扩散，且污染物从一个节点扩散到另一个节点的时间等同于水流从源节点输送到目标节点的最短时间，不考虑其他因素造成的污染物在管道扩散时的衰减作用。

③一旦污染物到达监测节点，监测设备能够立即提供及时的预警信息，并采取相应的措施，处理污染事故。检测设备具有高可靠性、高灵敏性。

④因为仿真软件并不能提供有关管道的精确计算结果，所以预警监测点只能设置在管网节点处，而非管道处。

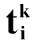
1.2 模型定义

基于以上概念，建立以下污染事件检测时间最短模型：

(1)

(2)

(3)

式中：NS为监测点数量；lj为二进制变量，表示节点j是否被选为监测节点，若是则lj取1,若不是则lj取0；L为监测节点集合。

污染事件检测时间最短模型是一个典型的搜索问题。随着管网节点数量的增多，可选的监测点配置方案数量快速增长，普通的全局搜索算法将不能满足计算的需求，故本文采用基于多线程机制的并行PSO算法来求解模型结果。

2 基于多线程机制的并行PSO算法

PSO算法源于对鸟群捕食行为的研究，类似于遗传算法，是一种基于迭代的寻优算法。由于该算法结构简单、过程易于理解，且算法本身的性能稳定、效率高，因而在众多优化问题模型中得到了广泛的应用[7]。

基本的粒子群算法中，问题的解空间被抽象为粒子位置的集合，通过粒子的移动来模拟寻找最优解的过程。每个粒子根据自身的历史最优位置和整个群体的全局最优位置，在一定的随机扰动下决定下一步的移动方向。假设搜索的解空间维度为D，粒子群体的数量为M，则可以用如下四个D维向量表示第i个粒子的信息。

粒子的当前位置为：

xi=(xi1,xi2,…,xiD)

(4)

粒子的历史最优位置为：

pi=(pi1,pi2,…,piD)

(5)

粒子的速度为：

vi=(vi1,vi2,…,viD)

(6)

整个粒子群的最优位置为：

Gi=(Gi1,Gi2,…,GiD)

(7)

粒子根据式(6)和式(7)更新速度和位置：

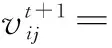
(8)

(9)

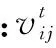
在本模型中，粒子搜索的空间维度D即监测点数；粒子i位置向量xi=(xi1,xi2,…,xiD)中，x为节点编号1～n(节点数量)的随机排序，约束条件为不能出现相同编号，粒子位置限制在[1,n]之间。

从基本的PSO算法看，其计算过程具有典型的并行计算特征，主要体现在[8]：①单粒子个体的位置、速度、个体历史最优解等更新是并行的；②整个群体的最优解评价是并行的；③下一代群体的产生是并行的。因此，基本的粒子群算法通过一个并行结构、用串行计算的方式来实现。

本文在标准并行粒子群优化算法的基础上，提出一种基于Java多线程编程模型的岛屿群体并行粒子群算法。将粒子群等分为几个小的群体，每个子群体在一个线程内独自进行计算和评价，以产生子群体的最佳粒子，并采用异步通信的方式，使子群体更新所在线程区域最优解时同步更新全局最优解[9-11]。

在本模型中，粒子的位置代表了监测网络节点的实际位置，在同一节点不可能设置两套设备，因此，粒子的位置向量不应包含重复的元素。为避免新产生的粒子违反上述约束条件，需要对粒子更新后的位置进行可行性判断，一旦发现不满足条件，需要局部更新产生粒子位置，以满足约束条件。算法中的更新动作主要通过对重复元素进行随机变异操作得到。同时，基本粒子群算法具有容易陷入局部最优解而无法跳出解空间的缺陷。在本文的模型中引入遗传算法中的变异概念，对新产生的粒子按一定的概率进行变异操作。

并行PSO算法求解流程如图1所示。

图1 并行PSO算法求解流程图

图1中：xi为粒子的位置;vi为粒子的当前速度;pi为粒子的历史最优位置;pg为全局最优位置;f(i)为粒子的适应度。每次粒子位置更新后，对新产生的连续解进行取整运算，并对产生的粒子进行合适性筛选。

3 模型计算流程

污染事件检测时间最短模型的求解流程如下。

①管网系统模型构建。采用EPANET软件构建管网系统模型[12]，编辑管网系统各节点、管道初始属性；设定供水管网系统供水模式，用来描述供水管网系统的供水量周期性变化规律；完成模型导入，将可视化模型拓扑图导出为管网描述文件，作为二次开发程序输入文件。

②二次开发程序编写。基于第一步导出的管网描述文件、EPANET toolkit编写二次开发程序，导出管网系统各管道长度、起始节点编号以及流量、流速时间序列数据。

③最短扩散时间矩阵构建。基于第二步获取数据，构建管网系统最短扩散时间矩阵T。根据第二步获取数据，构建一个简单的辅助矩阵P，P描述了平均状态下管网系统各管道内水流的流经时间。

P中元素p(i,j)通过式(10)计算得到：

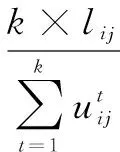
(10)

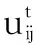
基于辅助矩阵P，利用图论算法中的最短路径算法可计算任意两个节点之间的最短扩散时间。t(i,j)为水流从节点i扩散到节点j所需的最短时间。

(11)

④模型求解。基于第三步获取的最短扩散时间矩阵T，利用基于多线程机制的并行PSO算法求解监测点布局方案。

通过这四步计算，可以得到监测节点选址的最终结果。最短检测时间模型计算流程如图2所示。

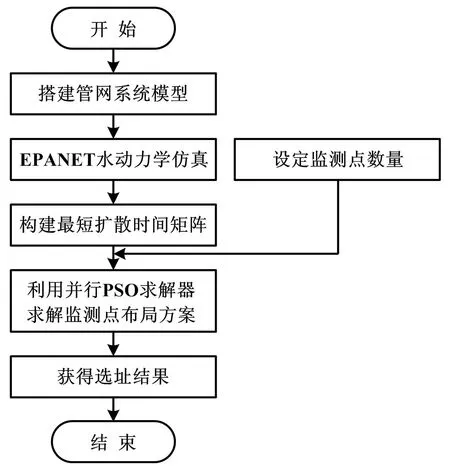
图2 最短检测时间模型计算流程图

4 仿真试验及结果分析

4.1 算例介绍

以EPANET软件自带的管网系统Net3为例，进行模型计算。Net3管网系统拓扑结构如图3所示。

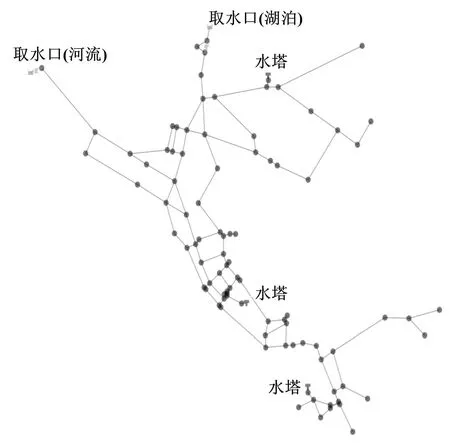
图3 Net3管网拓扑结构示意图

该管网系统包含主要节点97个、管道117条。其中，节点包括取水口2个、水塔3个、日常取水节点92个。该管网系统供水模式以24 h为周期，每个供水模式持续为1 h，因此该管网系统运行状态呈以24 h为周期的周期性变化趋势。

4.2 计算结果分析

利用第2节所述的方法，对该管网系统进行长时间水动力学模拟计算，并导出稳定状态下管网系统单供水周期内管道的流速、流量时间序列数据。然后，依据第1节提出的污染事件检测时间最短模型，编制基于Java多线程编程模型的代码，以优化求解不同监测点数量下供水管网水质监测传感器网络布局结果。

不同监测节点数目下的污染事件平均监测时间对比如图4所示。

图4 不同监测节点数目下的平均检测时间曲线

从图4中可以看出，当监测节点数量为9个时，可以将整个管网系统的平均污染事件检测时间限制在4 h之内；且节点数量从8个增加到9个时，检测时间明显缩短。综合考虑成本以及方案的有效性，认为监测点数量设置为9较为合适。

以设置9个监测点为例，图5给出了污染事件水质检测时间最短模型的布局方案拓扑结构。

图5 水质检测时间最短模型拓扑结构示意图

图5中，圆圈部分表示水质监测传感网络的布局节点。从图5中也可以看出，污染事件检测时间最短模型布局的结果一般具有较好的分散性，能够避免节点向供水量较大的节点集中。这是因为该模型是以整个系统任意节点遭受污染物注入情况的平均检测时间最短为目标，所以其优化结果必然具有较好的分散性。

在Intel i3处理器(双核四线程)的条件下，对比查看不同线程条件下本模型计算所需时间，结果如图6所示。

图6 不同线程条件下模型计算时间曲线图

通过图6可以看出，随着线程数量从1个增加到4个，模型的计算速度有较为明显的增加；而当线程数量从4个增加到5个时，受限于处理器本身的核心数量，速度提升并不明显。从图6也可以看出，通过多线程机制处理PSO算法可明显加快模型求解的速度，充分发挥了计算机硬件的作用。

5 结束语

针对供水管网系统水质监测网络布局问题，本文提出了污染事件检测时间最短模型。该模型以污染事件平均检测时间为优化目标，无需人为设定“服务水平”，所得布局方案监测点数量完全由预算决定；一旦给定监测点数量，能够保证污染事件平均检测时间最优，充分保证了模型的客观准确性；通过对供水管网系统运行状态平均化处理，提高了计算资源的空间利用率。同时，提出了基于多线程机制的并行PSO算法，提高了模型求解的效率。污染事件检测时间最短模型和基于多线程机制的并行PSO算法相结合，对实际的供水管网水质监测传感器网络布局设计具有一定的参考作用。

[1] WATSON J,GREENBERG H J,HART W E.A multiple objective analysis of sensor placement optimization in water networks[C]//American Society of Mechanical Engineers,2004.

[2] COZZOLINO L,MUCHERINO C,PIANESE D,et al.Positioning,within water distribution Networks,of Monitoring stations aiming at an early detection of intentional contamination[J].Civil Engineering and Environmental Systems,2006,23(3):161-174.

[3] KUMAR A,KANSAL M L,ARORA G.Detecting accidental contaminations in municipal water networks - discussion[J].Journal of Water Resources Planning and Management-ASCE,1999,125(5):308-309.

[4] KESSLER A,OSTEFELD A,SINAI G.Detecting accidental contaminations in municipal water networks[J].Journal of Water Resources Planning and Management,1998,124(4):192-198.

[5] OSTFELD A,SALOMONS E.Optimal layout of early warning detection stations for water distribution systems security[J].Journal of Water Resources Planning and Management-ASCE,2004,130(5):377-385.

[6] BERRY J W,FLEISCHER L,HART W E,et al.Sensor placement in municipal water networks[J].Journal of Water Resources Planning and Management-ASCE,2005,131(3):237-243.

[7] JORDEHI A R.Particle Swarm optimisation for dynamic optimisation problems:a review[J].Neural Computing & Applications,2014,25(7-8):1507-1516.

[8] 黄芳，樊晓平.基于岛屿群体模型的并行粒子群优化算法[J].控制与决策,2006,21(2):175-179,188.

[9] 马慧民，吴勇，叶春明.车辆路径问题的并行粒子群算法研究[J].上海理工大学学报,2007,29(5):435-439,444.

[10]王华秋，曹长修.基于模拟退火的并行粒子群优化研究[J].控制与决策,2005,20(5):500-504.

[11]沈林成，霍霄华，牛轶峰.离散粒子群优化算法研究现状综述[J].系统工程与电子技术.2008,30(10):1986-1990,1994.

[12]ELIADES D G,KYRIAKOU M,POLYCARPOU M M.Sensor placement in water distribution systems using the S-PLACE Toolkit[J].Procedia Engineering,2014,70:602-611.

Optimization of the Layout of Water Quality Monitoring Sensors Network for Water Distribution Network

SHEN Yifan，WEI Guanxiong，HOU Dibo，HUANG Pingjie，ZHANG Guangxin，ZHANG Hongjian

(College of Control Science and Engineering,Zhejiang University,Hangzhou 310027,China)

To deal with the sudden pollutant injection,the optimization of layout of water quality monitoring sensors for water distribution network has been more and more concerned in research.To against the shortcoming of the layout optimization based on the concept of “service level” which is easily to be disturbed by subjective factors,the model of the shortest detection time for pollution incident is proposed. With the average detection time of the pollution incident as the optimization object,the manual setting of “service level” is unnecessary,the number of the detection points of the layout strategy provided by the model is fully determined by budget,once the number of monitoring points is given,the average detection time of the pollution incident is optimum,and the objective accuracy of the model can be guaranteed.The status of the water distribution network is averaging processed to improve the spatial utilization of calculation resources.In addition,because the commonly used optimizing algorithms of model parameters cannot satisfy the requirement for large scale water distribution network,the parallel PSO algorithm based on multi-threading mechanism is also proposed.This fully plays the capability of multi-core processor,and enhances the utilization of hardware resource and the model calculation speed.The test results indicate that the model and algorithm proposed possess certain reference significance for layout optimization of water monitoring sensors in water distribution network.

Water distribution network; Water pollution; Water quality monitoring network; Parallel PSO algorithm; Node layout optimization; Model of the shortest detection time； Multithreading; Topology structure

国家自然科学基金资助项目(U1509208、61573313)、浙江省重点研发计划基金资助项目(2015C03G2010034)、中央高校基本科研业务费专项基金资助项目(2016FZA6004)

沈一凡(1991—)，男，在读硕士研究生，主要从事水质监测与预警技术的研究。E-mail:shenyf 0811@gmail.com。 侯迪波(通信作者)，男，博士，教授，主要从事先进传感技术、智能信息处理、环境监测预警等技术的研究。 E-mail:houdb@zju.edu.cn。

TH81;TP23

A

10.16086/j.cnki.issn1000-0380.201706012

修改稿收到日期:2016-03-16