基于星-凸形随机超曲面模型的扩展目标GM-PHD滤波器
魏 帅,冯新喜,王 泉
(空军工程大学信息与导航学院,西安 710077)
基于星-凸形随机超曲面模型的扩展目标GM-PHD滤波器
魏 帅,冯新喜,王 泉
(空军工程大学信息与导航学院,西安 710077)
针对扩展目标联合估计运动状态和目标外形的问题,提出一种基于星-凸形随机超曲面模型的扩展目标高斯混合概率密度滤波算法。该算法利用星-凸随机超曲面模型对量测的扩散程度进行建模,在高斯混合概率假设密度的框架下,通过求解、更新递推量测模型下的量测似然、新息等参数来实现对扩展目标的跟踪。仿真实验表明,该算法在保证跟踪有效性和可行性的同时,提高了对扩展目标运动状态和目标外形的估计精度。
星-凸形;随机超曲面模型;扩展目标;高斯混合概率密度
0 引言
近年来,随着传感器分辨率的不断提高以及目标与传感器距离的不断缩小,扩展目标的跟踪问题已成为跟踪领域的研究热点[1-4]。基于概率假设密度滤波器的多目标跟踪由于无需数据关联且能在处理跟踪问题的过程中同步获得动态目标数的估计,因此受到广泛关注。2009年,Mahler[5]推导获得了扩展目标PHD(extended-target PHD,ET-PHD)滤波器。2010年,Granstrom[6]等在线性高斯假设条件下给出了ET-PHD滤波器的高斯混合实现。在此基础上,文献[7]对高斯混合扩展目标概率假设密度滤波器的收敛性进行了分析,然而该算法假设量测分布在目标的边缘且制约了几何结构特性(椭圆或矩形)。文献[8]将随机矩阵与ET-PHD相结合,以混合高斯逆韦夏尔特分布近似目标强度分布。但算法假设量测噪声仅由目标扩散引起,忽略了传感器自身噪声,估计精度受限。针对此问题,文献[9]提出了一种基于椭圆随机超曲面模型的群目标高斯混合PHD滤波器,假设量测是由目标上散布的量测源产生并考虑传感器自身噪声,因此获得较高估计精度。然而由于外形椭圆的限制,难以灵活表征其它外形的扩展目标。
2011年,Baum[10]等提出利用星-凸(star-vertex)形对扩展目标外形进行建模,星-凸形可表征包括椭圆在内的更多样式的扩展目标外形,有更好的近似程度。因此,文中考虑利用星-凸随机超曲面模型对扩展目标的外形进行描述,结合ET-GM-PHD算法,提出基于星-凸形随机超曲面模型的扩展目标GM-PHD滤波器。该算法将目标状态参数和外形参数一起作为待估计向量,利用星-凸形随机超曲面模型对量测进行建模,同时给出ET-GM-PHD框架下量测似然等参数的求解和更新方法。仿真实验验证了算法的有效性和可行性。
1 星-凸形随机超曲面模型
1.1 星-凸形参数化表示
与点目标不同,扩展目标的状态信息xk包括目标运动状态信息xc,k和外形信息xs,k,分别由其质心和外形特征刻画。在数学上,星-凸形模型可以通过一维径向函数r(xs,k,θ)进行表示。如图1所示,径向函数边缘点的值仅与边缘点到原点中心的距离和角度θ有关。因此,可以将r(xs,k,θ)进行N阶傅里叶级数展开[11],即:
(1)
式中:θk∈[0,2π),扩展目标的外形信息可由向量表示,即:
xs,k=[ak0,ak1,bk1,…,akN,bkN]
(2)
(3)
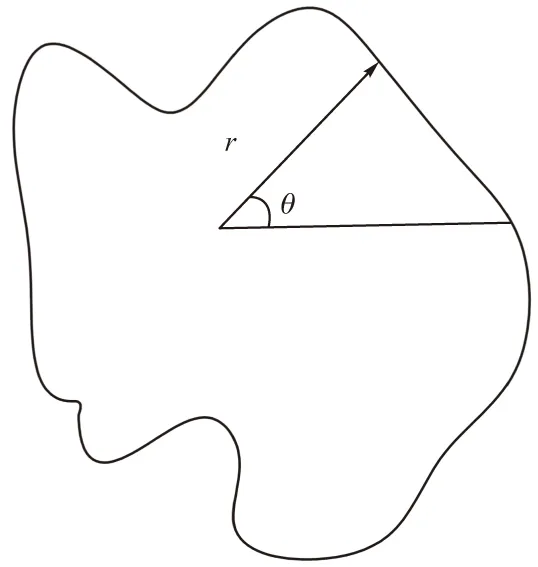
图1 星-凸形模型
1.2 星-凸形随机超曲面模型
对星-凸形扩展目标建模的一种有效的具体方法可采用随机超曲面模型[12](random hypersurface model,RHM)的形式,RHM是一种描述量测源分布的特殊模型。RHM模型认为量测源分布于缩小的目标真实形状上,即假设S(xs,k,xc,k)表示扩展目标的边界,sk,l表示缩放因子,则量测源可表示为:
zk,l,s=xc,k+sk,l(S(xs,k,xc,k)-xc,k)
(4)
因此,星-凸形RHM量测源模型可表示为:
zk,l,s=xc,k+sk,lr(xs,k,θk)e(θk)
(5)
e(θk)=[cos(θk) sin(θk)]T
(6)
则基于星-凸形RHM的量测模型表达式为:
zk,l=zk,l,s+vk,l=xc,k+sk,l·(S(xs,k,xc,k)-xc,k)+vk,l=xc,k+sk,lR(θk,l)xs,ke(θk,l)+vk,l
(7)
式中:θk是未知的,可以通过量测源zk,l,s和xc,k进行计算,sk,l近似服从高斯分布。
2 基于星-凸形随机超曲面模型的扩展目标跟踪
2.1 扩展目标高斯混合PHD滤波器
xi,k+1=Fkxi,k+Gkwi,k
(8)
式中:i=1,…,Nx,k,wi,k表示协方差为Qi,k的高斯白噪声。每个目标均服从相同的状态方程,且相互独立。
假设预测PHD高斯混合表示为
(9)
式中:Jk|k-1表示预测分量的数量;wj,k|k-1表示第j个分量的权值;mj,k|k-1和Pj,k|k-1分别表示第j个分量的预测均值和协方差。N(x;m,P)表示变量x服从均值为m、协方差为P的高斯分布。
假设量测个数服从泊松分布,则量测更新PHD可表示:
Dk|k(x|Z)=LZ(x)Dk|k-1(x|Z)
(10)
式中:LZ(x)表示量测伪似然函数,其表达式为
(11)
量测集合的划分对扩展目标跟踪结果具有较大的影响,文中采用文献[6]给出的基于距离的量测划分方法,具体方法参见文献[6]。
2.2 基于星-凸形随机超曲面模型的PHD更新
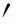
(12)
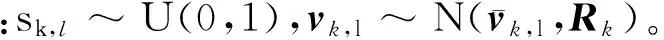
考虑量测某一划分情况下非空集合中的所有量测以及某一预测高斯项。由于目标运动方程为线性的,因此,预测均值mA,k|k-1和方差PA,k|k-1可通过卡尔曼滤波进行求解
(13)
(14)

(15)

(16)
(17)
(18)
(19))
由分析可知[11],对于星-凸形模型来说,必须对模型参数做一定限制,否则会出现不可预测的结果,即
(20)
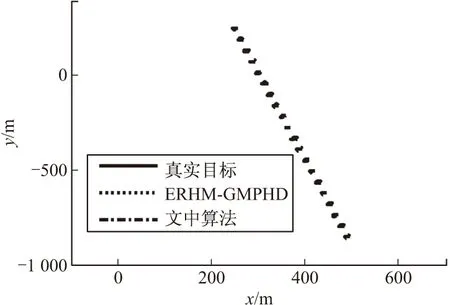
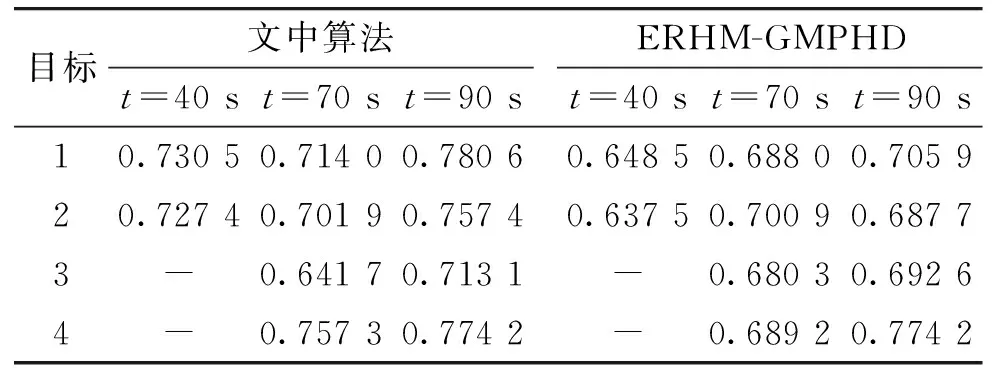
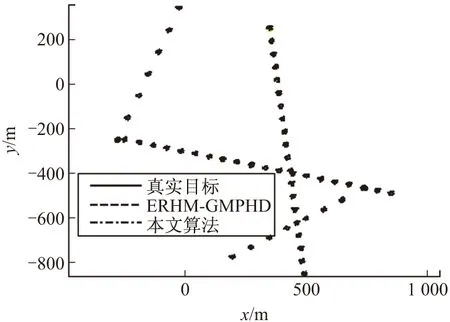
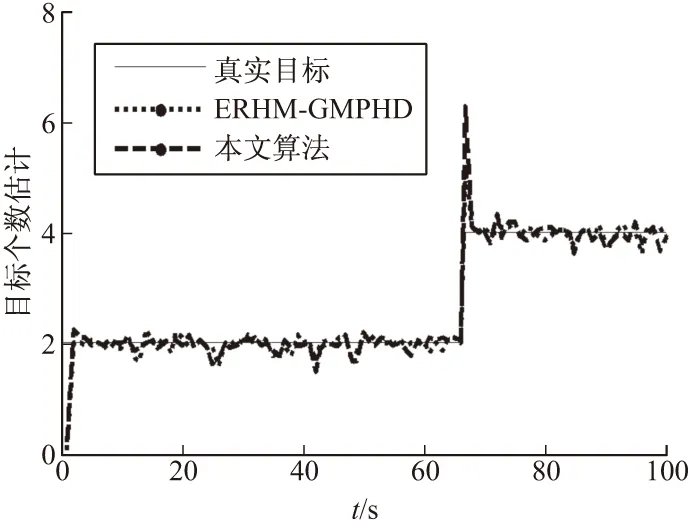
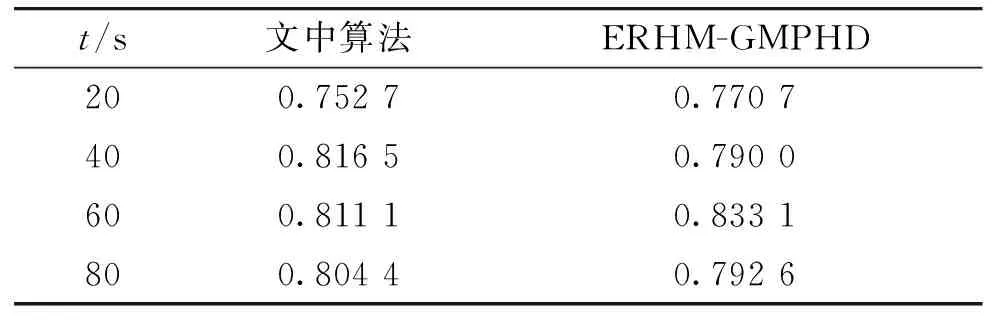
s.t.Lk (21) 式中:ck(xs,k)表示约束函数,Lk表示约束下界。对于ck(xs,k)的形式,文中采用采样约束[11]。当集合中所有量测均执行完上述操作后,可得到对应高斯分量的均值和协方差,从而可得量测似然为 (22) 将式(22)和对应的参数代入式(10)则可得到量测更新PHD。 文中将所提算法与基于椭圆随机超平面模型的扩展目标GM-PHD滤波器(ERHM-GMPHD)进行比较分析。分两个实验讨论,实验一讨论两种滤波器跟踪星-凸形扩展目标的情况;实验二分析两种滤波器跟踪椭圆形扩展目标的情况,并比较两种算法的跟踪性能。算法性能评估采用两个有形目标的交和两个有形目标的并的面积比值进行衡量[13](intersection-over-union,IOU),由于星-凸目标的特殊性,文中提出利用图像分析方法进行面积求解。面积求解思路为:步骤1:将图中需求解面积的部分进行分割并填色;步骤2:将图转换为灰度图;步骤3:将阈值法灰度图转成二值图像;步骤4:利用黑色/总像素的比值乘以图像的总面积,从而得到区域A的面积。 3.1 实验一 设二维观测区域为x∈[-1 000 m,1 000 m],y∈[-1 000 m,1 000 m],考虑单传感器跟踪4个目标的运动情况,传感器坐标为S=(1 000 m,0 m),3个目标相继出现,整个观测时间持续100 s,各目标初始状态以及出生和消亡的时间分别为:目标1:[350 m150/99 m/s250 m-1150/99 m/s1 s/100 s];目标2:[-250 m1150/99 m/s-250 m-250/99 m/s1 s/100 s];目标3:[650 m-500/33 m/s-520 m-280/33 m/s67 s/100 s];目标4:[-280 m-280/33 m/s-250 m650/33 m/s67 s/100 s]。目标运动状态表示为xk=[(xs,k)′,(xc,k)′]T,缩放因子sk,l∈N(0.7,0.05),采样周期T=1 s。考虑计算量,文中所提算法采用9阶傅里叶级数展开对目标的外形进行描述。则状态方程表示为:xk+1=Akxk+wk (23) 仿真参数设置最大高斯分量数目Jmax=100,修剪门限Tp=10-4,合并门限U=4,目标存活概率Ps=0.99,检测概率Pd=0.99。每一时刻每个目标产生的量测个数服从均值为6的泊松分布,杂波率为3,且在观测区域内均匀分布。量测噪声服从N(0,R),R=diag(0.62,0.62)。简单起见,不考虑目标衍生过程,新生目标的PHD为:Db(x)=0.1N(x;mb,Pb)+0.1N(x;-mb,Pb) (24) (25) 不考虑目标衍生过程,其对应的新生目标的PHD为:Db(x)=0.1N(x;mb,Pb)+0.1N(x;-mb,Pb) (26) 式中:mb=[10,10,0,250,0,250,0]T;Pb=diag(2,2,0.1,100,25,100,25)。其它参数设置与文中所提算法相同。 表1 各目标IOU值 图2给出了50次蒙特卡罗仿真实验平均后得到的跟踪结果图。从图2中粗略可以看出,文中所提算法和ERHM-GMPHD算法均能够较好的估计出目标运动的方向和轨迹。图3给出了估计结果局部放大图,进一步分析可知,ERHM-GMPHD算法虽然能将目标整个包含在估计椭圆内,但却无法估计出目标的形状。相反,文中算法能够对星-凸形目标的轮廓进行较为准确的估计。为衡量算法对目标外形估计的准确程度,文中采用IOU值作为评价指标。表1给出了4个目标在不同时刻的IOU值,从表中可以看出,文中所提算法估计得到各目标的IOU值总体上大于ERHM-GMPHD算法得到的IOU值,说明文中算法估计目标形状与真实目标形状之间具有较高的重合度,因此,文中算法可较为准确的估计出星-凸形目标的扩散外形。 图2 滤波结果 图3 局部结果放大图 图4和图5分别给出了50次蒙特卡罗仿真实验平均后得到的多目标个数估计随时间变化曲线和质心位置估计的OSPA曲线图。从图中可知,在目标个数发生变化的时刻,对两种算法而言,无论是目标个数估计曲线还是OSPA曲线,均具有较大的波动,但一旦进入目标数目恒定阶段,两种算法则可快速收敛,从而使得OSPA值迅速变小且准确估计出目标个数值,但从总体来看,文中算法对目标质心位置估计的OSPA距离更小,因此,相比于ERHM-GMPHD,文中算法在对星-凸外形目标外形轮廓进行准确描述的同时,对目标质心位置的估计精度也有所提高。 图4 目标数目估计 图5 OSPA距离 3.2 实验二 在本实验中,针对椭圆形目标,考察文中所提算法和基于椭圆随机超平面的模型的算法的跟踪性能。设二维观测区域为x∈[-1 000 m,1 000 m],y∈[-1 000 m,1 000 m],考虑单传感器跟踪单个目标的运动情况,传感器坐标为S=(1 000 m,0 m),采样周期T=1 s,各目标初始状态(350 m150/99 m/s250 m-1150/99 m/s),整个观测时间持续100 s。其它参数设置与实验一相同。 表2 不同算法IOU值 执行50次蒙特卡罗仿真,结果如图6和图7所示。从图6的滤波结果可以看出,文中算法和ERHM-GMPHD算法能够对椭圆形目标的运动轨迹进行较准确的估计。从图7的估计结果局部放大图可知,两种算法均能准确的估计出目标的轮廓,为进一步比较两种算法对目标外形估计情况,表2给出了两种算法在不同时刻的IOU值,从表中可以看出,两种算法对目标轮廓估计的IOU值较为接近,且均在0.8附近波动,说明估计目标与真实目标之间具有较高的重合度,因此,文中算法和ERHM-GMPHD对具有椭圆外形的单一扩展目标估计的能力一致,均能对椭圆形目标进行位置和外形的准确估计。为进一步验证文中算法跟踪椭圆目标的能力,文中在实验一的仿真参数环境下对具有椭圆外形的多扩展目标进行50次蒙特卡罗仿真实验,从实验结果可知,两种算法对多目标的轮廓估计的IOU值较为接近,且均在0.73附近波动,进一步说明了文中算法与ERHM-GMPHD对具有椭圆外形算法估计能力的一致性。图8给出了两种算法质心估计的OSPA距离曲线,从OSPA距离曲线可知,两种算法的估计结果均保持在较小的值,从而说明了两种算法的估计能力。 综上所述,文中给出的算法可跟踪包括椭圆在内的多种样式的扩展目标外形,且具有较准确的近似程度,然而,由于星-凸模型参数估计的复杂性,使得文中所提算法增加了运算复杂性,但从跟踪精确度和外形估计能力上看,文中所提算法跟踪能力优于ERHM-GMPHD算法。 针对扩展目标联合估计运动状态和目标外形的问题,提出了一种基于星-凸形随机超曲面模型的扩展目标GM-PHD滤波算法。分别对跟踪星-凸形扩展目标和椭圆形扩展目标情况进行了仿真实验,实验分析表明,文中所提的算法在保证跟踪有效性和可行性的同时提高了对扩展目标运动状态和目标外形的估计精度。下一步,将对算法的运算复杂性以及性能评估指标进行深入研究。 图6 滤波结果 图7 局部结果放大图 图8 OSPA距离 [1] GILHOLM K, SALMOND D. Spatial distribution model for tracking extended objects [J]. IEE Proceedings:Radar, Sonar and Navigation, 2005, 152(5): 364-371. [2] GILHOLM K, GODSILL S, MASKELL S, et al. Poisson models for extended target and group tracking [J]. SPIE Processing, 2005, 5913: 230-241. [3] KOCH J W. Bayesian approach to extended object and cluster tracking using random matrices [J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 1042-1059. [4] MAHLER R P S. Multitarget Bayes filtering via first-order multitarget moments [J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178. [5] MAHLER R. PHD filters for nonstandard targets: I Extended targets [C]∥12th International Conference on Information Fusion, 2009: 915-921. [6] GRANSTRÖM K, LUNDQUIST C, ORGUNER U. A Gaussian mixture PHD filter for extended target tracking [C]∥13th International Conference on Information Fusion, 2010: 1-8. [7] 连峰, 韩崇昭, 刘伟峰. 高斯混合扩展目标概率假设密度滤波器的收敛性分析 [J]. 自动化学报, 2012, 38(8): 1343-1352. [8] GRANSTRÖM K, ORGUNER U. A PHD filter for tracking multiple extended targets using random matrices [J]. IEEE Transactions on Signal Processing, 2012, 60(11): 5657-5671. [9] 张慧, 徐晖, 王雪莹, 等. 一种基于椭圆随机超曲面模型的群目标高斯混合PHD滤波器 [J]. 光学学报, 2013, 33(9): 0904001-1-0904001-10. [10] BAUM M, HANEBECK U D. Shape tracking of extended objects and group targets with star-convex RHMs [C]∥14th International Conference on Information Fusion, 2011:338-345. [11] SUN Lifan, LAN Jian, LI X, et al. Extended target tracking using star-convex model with nonlinear inequality constraints [C]∥Proceedings of the 31st Chinese Control Conference, 2012: 3869-3874. [12] BAUM M, HANEBECK U D. Random hypersurface models for extended object tracking [C]∥IEEE International Symposium on Signal Processing and Information Technilogy (ISSPIT), 2009: 178-183. [13] GRANSTRÖM K, LUNDQUIST C, ORGUNER U. Tracking rectangular and elliptical extended targets using laser measurements [C]∥14th International Conference on Information Fusion, 2011:592-599. A Gaussian Mixture PHD Filter for Extended Target Based on Star-convex Random Hypersurface Model WEI Shuai,FENG Xinxi,WANG Quan (Information and Navigation College, Air Force Engineering University, Xi’an 710077, China) A Gaussian mixture PHD filter for extended target tracking based on star-convex random hypersurface model was proposed for the problem of joint estimation of the extended target shape and motion state. The proposed algorithm modelled the diffusion degree of measuration by using the star-convex random hypersurface model. Then, the extended targets were tracked by calculating and updating the measurement likelihood and innovation under the Gaussian mixture probability hypothesis density framework. The simulation results showed that the proposed method could guarantee the tracking availability and feasibility and improve the estimated accuracy of extended target motion state as well as the target shape. star-convex; random hypersurface model; extended target; Gaussian mixture probability hypothesis density 2016-03-19 国家自然科学基金(61571458);陕西省自然科学基金(2011JM8023)资助 魏帅(1993-),女,北京人,硕士研究生,研究方向:目标跟踪。 TN953 A3 仿真实验分析
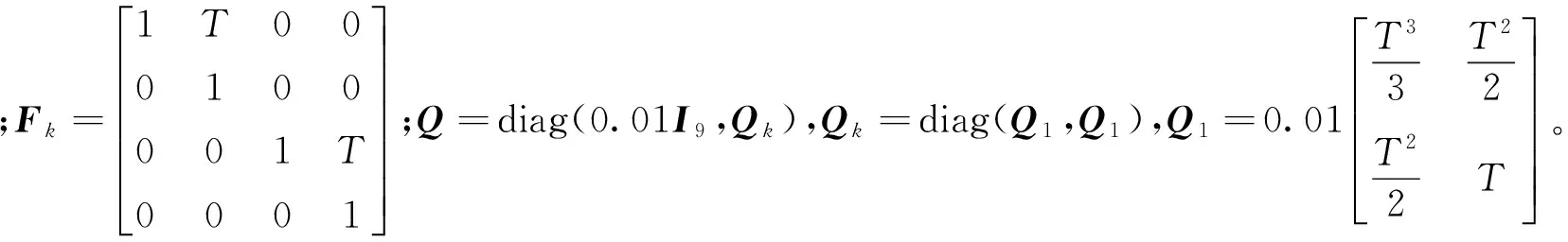


4 总结