UKF滤波算法在弹箭落点估计中的应用

曾凡桥,陈国光,高小东,刘 霖

(1 中北大学机电工程学院,太原 030051;2 豫西工业集团有限公司,河南南阳 473000)

UKF滤波算法在弹箭落点估计中的应用

曾凡桥1,陈国光1,高小东2,刘 霖1

(1 中北大学机电工程学院,太原 030051;2 豫西工业集团有限公司,河南南阳 473000)

依据部分弹道的弹道轨迹测量数据,准确预报弹道落点,是弹道修正弹药智能化的关键技术。综合考虑滤波精度和算法复杂度,文中采用质点弹道模型和无迹卡尔曼滤波(unscented Kalman filter)方法,建立了弹道滤波模型和外推弹道模型。通过对雷达测量数据的处理结果表明,UKF弹道滤波模型和质点外推模型有较高的精度。

UKF;弹道落点;雷达;弹道滤波

0 引言

在现代战争中,为减少不必要的附加损伤,要求弹箭具有精确的点目标打击能力,弹道修正弹就是诸多新型弹药中低成本、高精度的炮兵常规弹药之一。其中大口径弹道修正弹药,利用探测系统实测弹箭在空中飞行的一段数据,然后对量测数据进行处理,辨识出重要的气动参数,将预估弹箭落点与观测的目标信息对比,获得的弹道偏差为修正指令提供依据。然而,雷达探测系统或全球定位系统(GPS)在测量弹箭飞行参数的过程中,会有各种随机因素的干扰使得测量数据中含有噪声[1-3]。

文中针对雷达探测弹箭飞行时的量测数据误差较大,在一定程度上影响弹道落点的预估。提出采用无迹卡尔曼滤波对量测数据进行滤波处理,避免引入模型的线性化误差,提高了滤波精度,从而提高了对弹箭落点估计的准确度。

1 外推弹道模型

弹箭飞行过程中,信息处理系统需要利用雷达已探测到的一段数据进行弹道滤波,辨识出相应的参数,并对其后续飞行弹道进行预估,这就要求我们应该选取合适的简化弹道模型,满足弹箭落点解算的快速性、实时性[4]。

(1)

2 量测方程

球面坐标系下雷达测量得到斜距γ、方位角β和高低角ε,假定雷达坐标系RxRyRzR与地面坐标系Oxyz的关系如图1所示[5]。

图1 雷达坐标系、雷达测量值与地面坐标系的关系

由图1可得,雷达测量值与地面坐标系的关系:

(2)

3 滤波模型建立

根据雷达坐标系与地面坐标系的关系,用测量得到的6个参数和式(1)辨识出弹箭在空中飞行时的弹道系数c,就需要用到一段量测值和理论弹道模型式(1)构造气动参数辨识模型。

弹道滤波状态变量取x、y、z、vx、vy、vz、c,即:

(3)

将弹道系数c视为常量,则弹道模型的动态方程为:

(4)

在非线性方程(3)中引入随机高斯白噪声n,是为了补偿对弹箭质心运动近似描述时存在的误差。n是服从均值为零且方差为Q的正态分布,即n～N(0,Q)。

Z=h(X)+V=

(5)

式中:V是雷达测量噪声且假定V～N(0,R),其中:

(6)

4 UKF滤波算法

UKF对状态向量的后验概率密度函数(PDF)进行近似化,利用Sigma采样点对高斯分布的统计特性进行传递,得到的后验均值和协方差都能精确到二阶,且不需要对非线性系统进行线性化,可以很容易的应用于非线性系统的状态估计,因此,UKF方法在许多方面都得到了广泛应用[6]。

UKF使用的是离散时间非线性模型,因此需要对系统模型进行离散化处理,文中采用四阶Runge-Kutta法以多步数值积分的形式实现。

处理后的系统模型和观测模型[7]为:

(7)

(8)

具体解算步骤如下:

步骤1:滤波初值初始化

(9)

(10)

步骤2:Sigma点选取

(11)

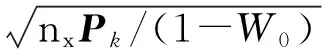
步骤3:状态预测

根据状态方程(7)可以得到每个Sigma采样点的一步预测:

(12)

则k+1时刻的状态一步预测值及预测方差如下:

(13)

(14)

步骤4:观测更新

将Sigma点代入式(8)的观测方程,可得:

(15)

(16)

(17)

步骤5:状态更新

(18)

(19)

(20)

(21)

式中Zk+1为k+1时刻的实际观测值。

5 仿真计算

文中以一种典型的大口径炮弹为例,对其进行数值仿真计算。在仿真中,采用高精度弹道模型生成理论弹道,叠加雷达测量随机误差后作为雷达量测数据。用上述滤波方法对测量值处理,然后外推弹道进行落点(X,Z)估计,比较计算弹道偏差。仿真分析中雷达采样间隔0.1 s,雷达测量误差设定为:σγ=10 m;σβ=0.001 5 rad;σε=0.001 5 rad。

弹丸发射2 s后模拟雷达开机开始跟踪测量,现选取第29～55 s内的量测数据,首先将其坐标变换到地面坐标下,然后进行滤波处理。图2、图3、图4给出了X、Y、Z3个方向量测值与理论弹道的差,图5、图6、图7给出了X、Y、Z3个方向滤波结果与理论弹道的差。

滤波结束后选取第55 s时滤波数据,代入质点弹道模型进行计算得到后续弹道,并与生成的理论弹道进行对比,得出落点偏差见图8～图11和表1。

图2 X方向量测值与理论弹道的差

图3 Y方向量测值与理论弹道的差

图4 Z方向量测值与理论弹道的差

图5 X方向滤波结果与理论弹道的差

图6 Y方向滤波结果与理论弹道的差

图7 Z方向滤波结果与理论弹道的差

图8 射程与射高的关系图

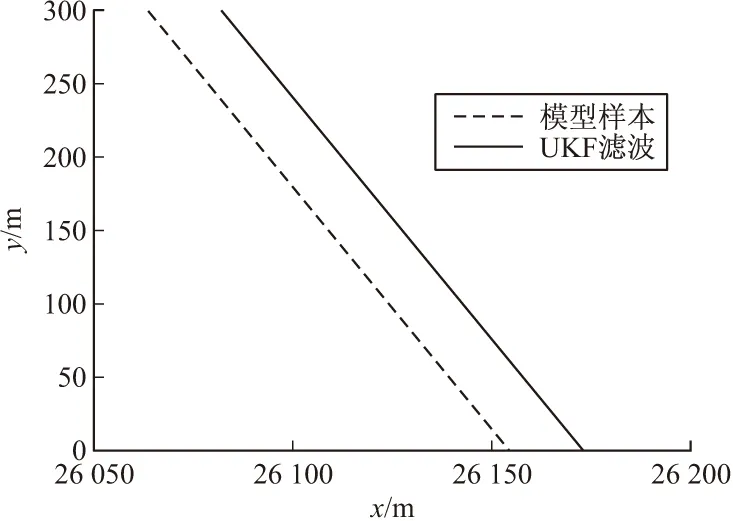
图9 射程与射高的关系放大图

X/mZ/m理论落点26162.874726.962外推落点26176.67735.253落点偏差13.7968.291

6 结论

文中利用地面侦查雷达测得弹箭的一段飞行参数,采用无迹卡尔曼滤波算法对带有随机噪声的雷达量测数据进行滤波处理。将滤波结束时的状态估计量代入质点弹道模型,外推出弹道落点,为有控弹箭的修正提供了有效的数据。计算结果表明,对于随机性和幅值较大的量测数据,用UKF滤波算法处理后的数据有较好的收敛性和稳定性,通过与理论落点对比,基于无迹卡尔曼滤波最优估计方法的弹道预报有着较高精度,对弹箭落点的估计可得出令人满意的结果。

图10 射程与射偏的关系图

图11 射程与射偏的关系放大图

[1] 王志军, 尹建平. 弹药学 [M]. 北京: 北京理工大学出版社, 2005: 2-4.

[2] 史金光, 刘猛, 曹成壮, 等. 弹道修正弹落点预报方法研究 [J]. 弹道学报, 2014, 26(2): 29-33.

[3] 高敏, 张强. 弹道修正弹实际弹道探测技术综述 [J]. 弹道学报, 2003, 15(1): 87-92.

[4] 徐明友. 高等外弹道学 [M]. 北京: 高等教育出版社, 2003: 174-175.

[5] 常思江, 王中原, 牛春峰. 基于卡尔曼滤波的弹箭飞行状态估计方法 [J]. 弹道学报, 2010, 22(3): 94-98.

[6] 何友, 修建娟, 张晶炜, 等. 雷达数据处理及应用 [M]. 北京: 电子工业出版社, 2006: 46-47.

[7] 徐强, 包伯成, 杨晓云, 等. 蔡氏电路方程的离散化与数字电路实现 [J]. 计算机应用研究, 2011, 28(6): 2158-2160.

[8] JULIER S J, UHLMANN J K. Unscented filtering and nonlinear estimation [J]. Proceedings of the IEEE, 2004, 92(3): 401-422.

Application of Unscented Kalman Filter Filtering Algorithm in Estimation of Projectile Point of Fall

ZENG Fanqiao1,CHEN Guoguang1,GAO Xiaodong2,LIU Lin1

(1 School of Mechatronics Engineering, North University of China, Taiyuan 030051, China; 2 Yuxi Industries Group Co. Ltd, Henan Nanyang 473000, China)

According to the measured data of part of ballistic trajectory to accurately predict the trajectory’s point of fall, it was the key technology of trajectory correction ammunition intelligence. Considering the filtering accuracy and complexity of the algorithm, the ballistic filtering model and the extrapolated trajectory model were established by using particle trajectory model and unscented Kalman filter method in this paper. The processing results of the measured data obtained by radar showed that the UKF trajectory filtering model and the particle extrapolation model had higher accuracy.

unscented Kalman filter; trajectory’s point of fall; radar; ballistic filtering

2016-04-30

曾凡桥(1989-),男,重庆人,硕士研究生,研究方向:弹箭飞行与控制技术。

TJ410.1

A