基于仿真的某中口径舰炮弹丸入水前冲过载
董盛鹏,王雨时,李作华,张志彪,闻 泉
(1 南京理工大学机械工程学院,南京 210094;2 辽宁华兴机电有限公司,辽宁锦州 121017)
基于仿真的某中口径舰炮弹丸入水前冲过载
董盛鹏1,王雨时1,李作华2,张志彪1,闻 泉1
(1 南京理工大学机械工程学院,南京 210094;2 辽宁华兴机电有限公司,辽宁锦州 121017)
为了为某舰炮弹丸弹底触发引信惯性前冲发火机构对海射击时的动态特性设计和评估提供参考,借助ANSYS/LS-DYNA软件,采用任意拉格朗日-欧拉方法,仿真了该弹丸不同落速、不同落角的入水过程,得到不同落速、落角和是否自转等条件下的弹丸入水前冲过载。落速或落角越大,前冲过载越大、过载峰值宽度越小;小落角入水过程中弹丸姿态不稳定,易发生跳弹,使前冲过载减小,甚至消失,并产生较大径向过载;自转对该弹丸入水前冲过载影响较小,可忽略;落速250 m/s、落角5°时的过载是引信惯性发火机构发火准确性设计要考虑的可信极限弹道环境,前冲过载峰值约为287g,持续时间约为1 ms。
舰炮弹丸;仿真;弹道环境;引信;入水冲击;前冲过载
0 引言
目前,对于入水问题的研究主要采用试验和数值仿真两种方法。试验研究方法耗资巨大且操作困难,因而大多集中于低速条件下。相比试验研究成本高、周期长、结果不精确等缺点,数值仿真方法具有明显优势。随着计算机技术和有限元技术的发展,计算速度和计算精度已有极大提高,利用有限元方法仿真分析此类瞬态动力学问题,能极大提高研究效率,节约研究成本[1-3]。
文献[4]通过LS-DYNA仿真得出低速子弹垂直入水冲击过载峰值与入水速度之间为线性关系,随入水速度增大而增大。文献[2]应用商用计算流体动力学软件,使用流体体积函数模型并结合动网格技术,仿真了平头回转体模型在亚音速、跨音速以及超音速状态下的入水过程,得到不同速度下入水阻力特性、头部直径、液体可压缩性及空气激波对入水过程的影响。文献[5]采用光滑粒子流体动力学方法对圆柱结构入水冲击过程进行三维数值模拟并通过自行设计实验装置及高速摄影系统,对圆柱体入水过程进行了实验研究。文献[6]基于非线性显式动力分析方法采用任意拉格朗日-欧拉算法,对楔形体垂直入水的初期过程进行数值仿真,分析了楔形体底部压力分布情况,讨论了网格密度、接触刚度以及阻尼系数对数值计算结果的影响,并将数值结果与理论结果对比,验证了任意拉格朗日-欧拉方法的可信性。
研究入水冲击的文献较多,但尚未见有对回转体小落角高速入水问题的研究。文中对某中口径舰炮弹丸以不同落角、不同速度入水过程进行数值仿真研究,分析前冲过载变化规律,为其引信惯性发火机构动态特性设计和评估提供参考。
1 仿真方法
1.1 任意拉格朗日-欧拉方法简介
任意拉格朗日-欧拉(arbitrary Lagrangian-Eulerian)方法按英文词头简称ALE方法,最初出现在数值模拟流体动力学问题的有限差分法中。该方法兼具Lagrange方法和Euler方法的特点,即它首先在结构边界和运动处理上引进了Lagrange方法的特点,因此能有效跟踪物质结构边界运动;其次在内部网格划分上,吸收了Euler方法的长处,使内部网格独立于物质存在,但又不完全同于Euler网格,其内部网格可根据定义参数在求解过程中适当调整位置,使得网格不至于发生严重畸变。该方法非常适合于分析大变形问题。使用该方法时网格与网格间的物质是可流动的[7]。
LS-DYNA程序为流构耦合作用研究提供了合适的材料模型和必要的状态方程,并在任意拉格朗日-欧拉算法中提供了对流和耦合算法,可提供精确、稳定、守恒且单调的数值计算结果。任意拉格朗日-欧拉算法可系统地计算所有单元质量、动量和能量运输,而单元密度、速度和能量等参量可随时间更新,然后采用更新后的密度和模型状态方程中单位内能来计算单元中的压力值[8]。
1.2 仿真模型
文中分析的舰炮弹丸口径为76.2 mm,弹丸质量5.9 kg,弹丸长度365 mm。
建立由水、空气和弹丸三部分组成的三维仿真模型,均采用SOLID 164实体单元。弹丸应用Lagrange算法;空气和水域采用欧拉材料,应用任意拉格朗日-欧拉多物质算法。为避免模型边界影响计算结果,在水域和空气边界上施加无反射条件。由于要计算倾斜入水,且弹丸自转,所以须建立整体模型。在水和空气交界面上,物质变形和运动剧烈,故加密网格,其余采用均匀网格。弹丸网格划分模型如图1所示,空气域和水域模型如图2所示。
图1 弹丸网格划分

图2 空气和水域模型
空气和水材料模型为LS-DYNA中的*MAT_NULL流体模型,采用格吕内森状态方程定义压力与体积关系,水(海水)与空气材料模型参数如表1所列。弹丸入水过程中不会出现明显变形,因而为了在不影响准确性的前提下提高求解效率,选用LS-DYNA中的刚体材料模型*MAT_RIGID,通过关键字*PART_INERTIA设置弹丸质量、质心、各向转动惯量、速度矢量、转速及转轴。

表1 海水和空气参数[4]
1.3 仿真基本假设
a)不涉及弹丸内部,只保留外形;
b)保证质量、质心、转动惯量等参数一致;
c)忽略弹带、膛线影响;
d)速度方向、弹丸转轴与弹丸几何轴线重合;
e)海面为平面且静止;
f)弹丸右旋,不同落角、速度下均假设转速ω=11 000 r/min。
2 仿真结果
弹丸入水前冲过载与入水速度和角度有关。下面分别取5°、10°、15°、30°、45°、60°落角,250 m/s、450 m/s、600 m/s、750 m/s、900 m/s落速,分析入水过程。
2.1 15°、30°、45°、60°落角入水分析
图3为弹丸以15°、30°、45°、60°落角和900 m/s落速入水500 μs时的状态。可知弹入水过程中,与水直接接触的只有弹头部的小圆台。水与弹头部接触后,受到弹头部冲击,迅速向四周流动,随着弹丸不断深入,形成开口空泡并不断发展。图4~图7分别为15°、30°、45°、60°落角在不同落速下的前冲过载曲线。
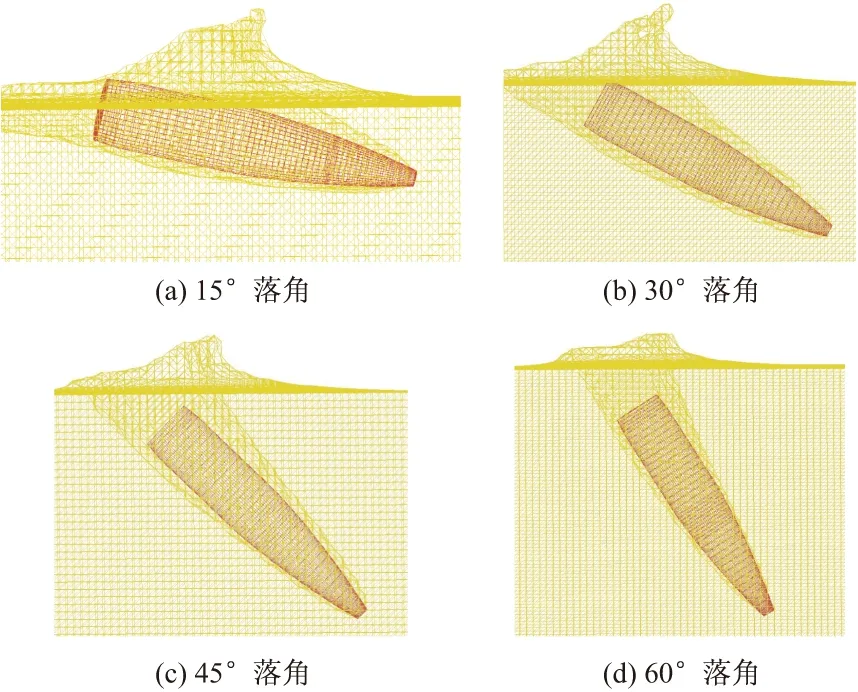
图3 900 m/s速度入水500 μs时的状态

图4 不同速度15°落角前冲过载曲线

图5 不同速度30°落角前冲过载曲线
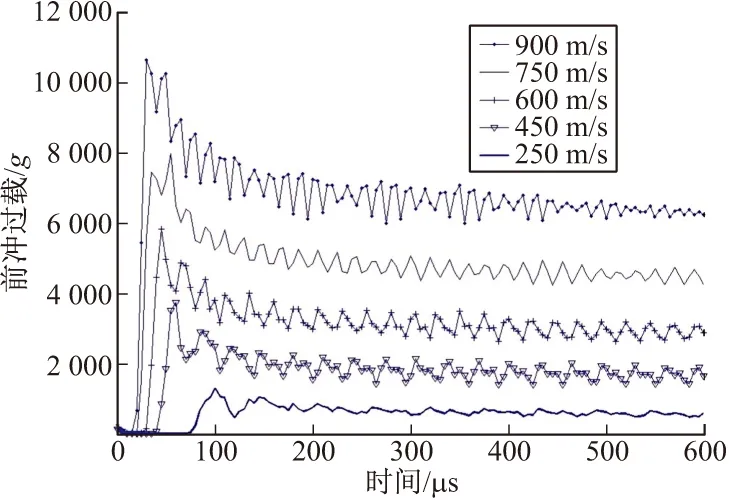
图6 不同速度45°落角前冲过载曲线
由图4~图7分析可得,入水速度越高,前冲过载越大,峰值宽度越小;落角越大,其峰值越大,峰值宽度越小。随着弹头部逐渐侵入水中,水的阻力迅速增大,当头部圆台刚好完全侵入水中时阻力最大,此时弹丸前冲过载也最大。随着弹头部彻底侵入水中,前冲过载随速度衰减伴随着波动而逐渐降低。

图7 不同速度60°落角前冲过载曲线
图8~图11分别给出了15°、30°、45°、60°落角,900 m/s落速下径向过载与前冲过载曲线。图12给出了15°落角,250 m/s、450 m/s、600 m/s和750 m/s落速下径向过载与前冲过载曲线。
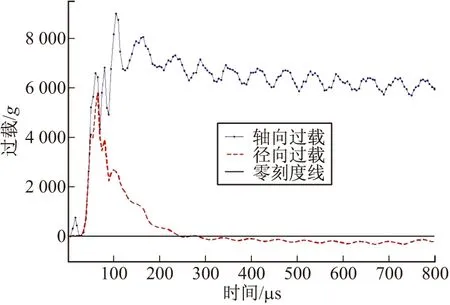
图8 15°落角、900 m/s轴向与径向过载
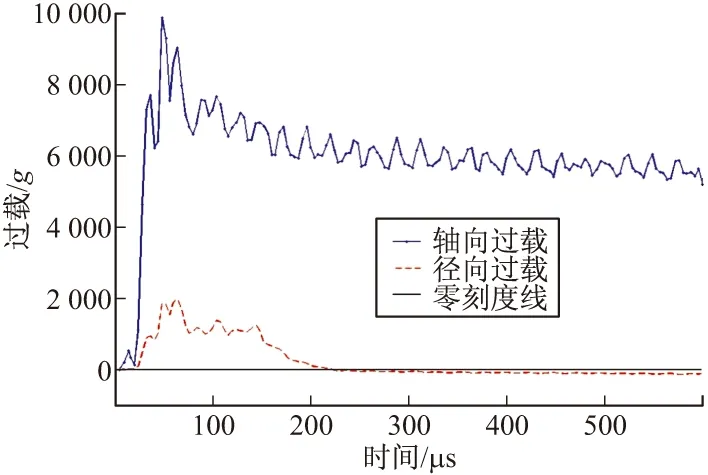
图9 30°落角、900 m/s轴向与径向过载
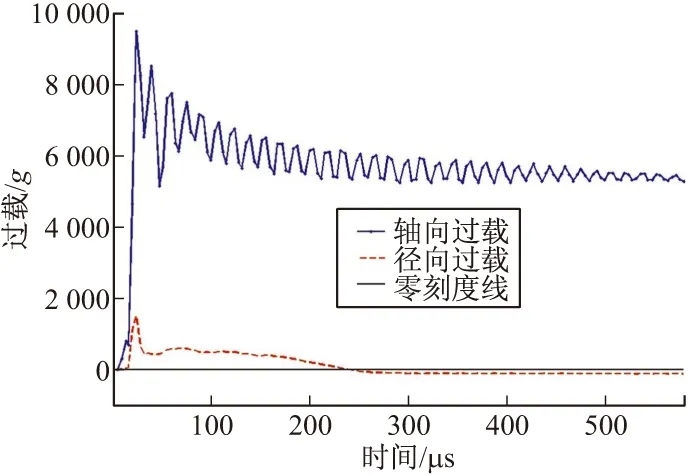
图10 45°落角、900 m/s轴向与径向过载
由图8~图11可得,弹丸径向过载峰值与前冲过载峰值出现时刻相近,入水落角越大弹丸所受到的径向过载相对于前冲过载越小。因该径向过载出现峰值时间短,相对于轴向过载较小,故大落角入水时可不予考虑其对引信惯性发火机构的影响。

图11 60°落角、900 m/s轴向与径向过载
2.2 5°和10°落角入水分析
落角为5°、10°时,在250 m/s到900 m/s的速度下,舰炮弹丸均发生了图13和图14所示的跳弹现象。
小落角入水时弹身偏转较大。应用MATLAB软件可求解弹丸沿弹轴方向和垂直于弹轴方向的过载,轴向过载即为弹丸前冲过载,垂直于弹轴方向的过载则为径向过载。
图15和图16分别为不同落速下、落角为5°、10°的前冲过载和径向过载曲线。由图15和图16可知,小角度落水过程中,随着弹丸方向的偏离,其前冲过载减小至零,甚至产生反方向的过载;弹身与水直接接触导致弹丸径向过载急剧增大,其峰值远远大于轴向过载峰值,该过载能增大引信惯性触发的轴向运动件的摩擦,有可能使引信惯性发火机构失效。
在所计算的5°~60°落角范围内,5°落角条件下前冲过载最小。对应250 m/s落速的过载是引信惯性发火机构发火正确性设计要考虑的可信极限弹道环境,在4.62 ms内前冲过载和径向过载系数如表2所列。
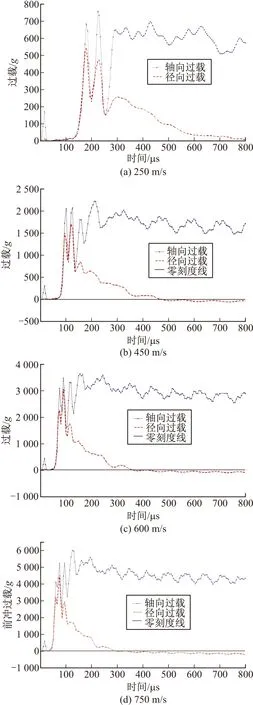
图12 15°落角不同速度下轴向与径向过载曲线

图13 5°落角入水过程

图14 10°落角入水过程
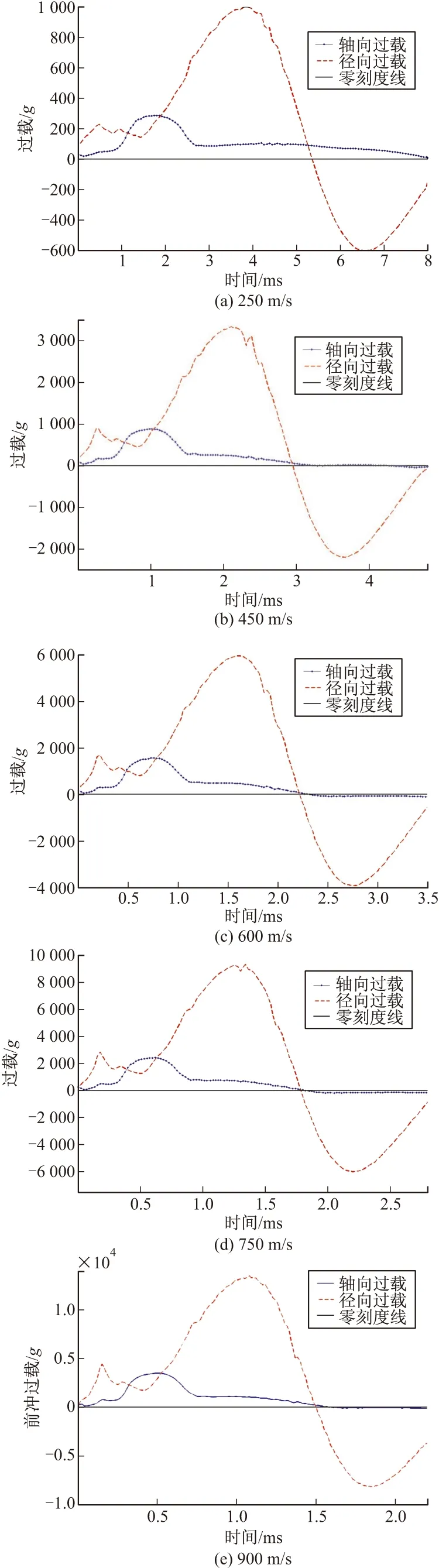
图15 5°落角、不同落速下前冲过载和径向过载曲线
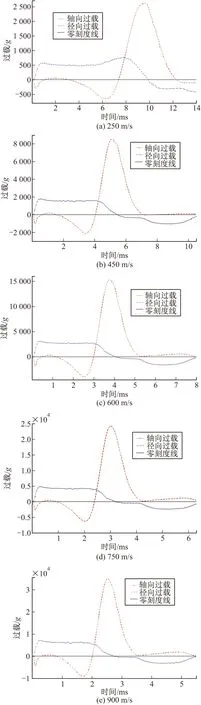
图16 10°落角、不同落速下前冲过载和径向过载曲线
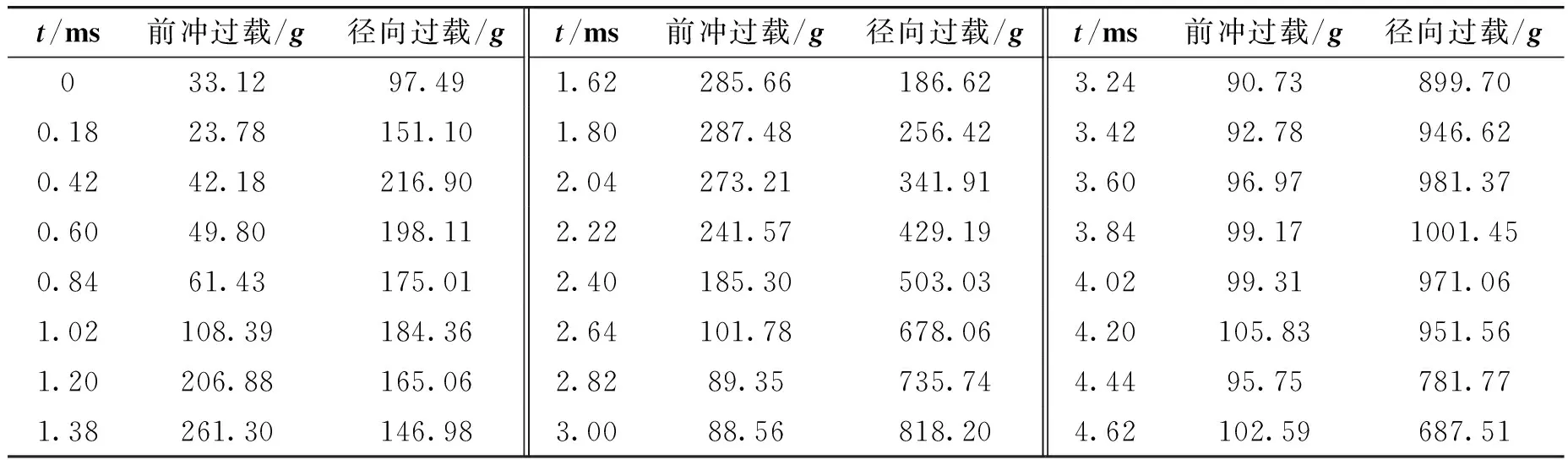
t/ms前冲过载/g径向过载/gt/ms前冲过载/g径向过载/gt/ms前冲过载/g径向过载/g033.1297.491.62285.66186.623.2490.73899.700.1823.78151.101.80287.48256.423.4292.78946.620.4242.18216.902.04273.21341.913.6096.97981.370.6049.80198.112.22241.57429.193.8499.171001.450.8461.43175.012.40185.30503.034.0299.31971.061.02108.39184.362.64101.78678.064.20105.83951.561.20206.88165.062.8289.35735.744.4495.75781.771.38261.30146.983.0088.56818.204.62102.59687.51
2.3 弹丸前冲过载峰值分析
仿真得不同落角、不同落速入水时该舰炮弹丸前冲过载峰值如表3所列。

表3 弹丸不同落角、速度落水时前冲过载
运用MATLAB软件对弹丸不同落角、不同落速下入水前冲过载峰值进行最小二乘法拟合,不同落角下的拟合曲线见图17。入水落角φ在5°~60°、落速v在250~900 m/s之间时,弹丸入水前冲过载峰值k4max为:
k4max=(aφ+b)exp(kv)
(1)
式中:k为入水速度相关系数,v∈(250 m/s,900 m/s)时,k≈0.028 5;a、b为入水角度相关系数,φ∈(5°,60°),a、b分别为25.28、146.9。
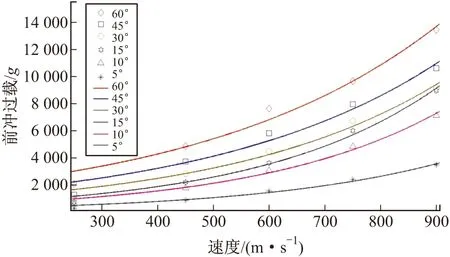
图17 不同落角不同落速下入水前冲过载峰值拟合曲线
据上述结果知,舰炮弹丸以落角5°~60°、落速250~900 m/s倾斜入水时,弹丸前冲过载值随落水速度增大而增大,并近似呈指数关系增大;同时随落角增大而增大,并近似呈线性关系增大。
2.4 弹丸自转对入水过程的影响
分别利用10°和60°落角、900 m/s落速入水模型,将其转速设置为零,分别与带自转结果对比,发现60°落角条件下加速度曲线、速度曲线、位移曲线与带自转的无明显差别。10°落角下径向过载、前冲过载曲线也相差不大,如图18所示。图19为10°落角下带自转弹丸侧向即Z向(以射向为X方向,垂直向上为Y方向,则弹道平面为XOY,按右手法则确定Z方向为弹道平面XOY的右侧)位移和速度曲线。自转弹丸沿侧向有微小位移,弹丸发生偏转的原因是由于弹丸自转带动其周围水介质流动,使其左右受力不均,产生马格努斯效应[9],弹丸发生轻微偏转。

图18 自转与不自转弹丸前冲过载、径向过载曲线
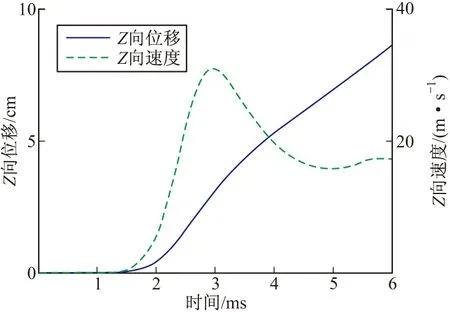
图19 Z轴方向速度与位移曲线
由此可知小落角入水过程中有马格努斯力存在,其方向垂直于竖直平面。前面分析的径向过载均忽略了马格努斯力,即该过载在XOY平面内。
250 m/s落速、5°和10°落角下其前冲过载曲线、XOY平面内的径向过载曲线、马格努斯过载曲线以及总径向过载曲线(XOY平面内的径向过载与马格努斯过载的几何和)如图20和图21所示。
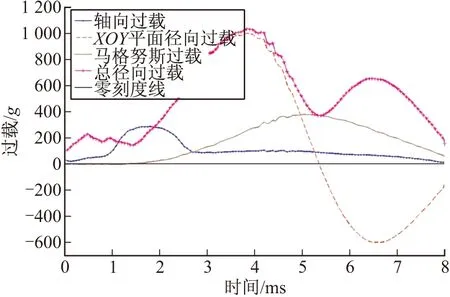
图20 5°落角各过载

图21 10°落角各过载
由图20和图21可知马格努斯力主要作用在前冲过载峰值结束时刻,该时刻引信已经完成惯性发火。且马格努斯过载的存在,使总的径向过载增大并不明显。可见马格努斯力对弹丸惯性发火机构的影响较小。
因此,弹丸是否自转对于前冲过载影响不大。大落角入水时,无马格努斯力产生,可忽略弹丸自转影响;小落角入水时,弹丸自转对总的径向过载有一定影响,但对引信惯性发火机构的影响较小,也可以忽略。
3 仿真可信性说明
为验证仿真可信性,将仿真得到的弹丸垂直入水时的减加速度数值与经验公式估算值比较。杜马公式是估算载体侵彻水介质时减加速度的经验公式[10]:
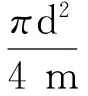
(2)
式中:αJ为弹丸受水介质阻力时的减加速度(m/s2);d为弹丸与水接触部位直径(m);m为弹丸质量(kg);ρw为水介质密度(kg/m3);v为弹丸着速(m/s);Cx为弹丸在空气中的阻力系数。
弹丸垂直入水过程中只有头部圆台与水直接接触,故与水接触直径d=0.018。
弹丸在空气中的阻力系数取弹丸在不同马赫数下Fluent计算所得的平均值Cx=0.38。
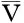
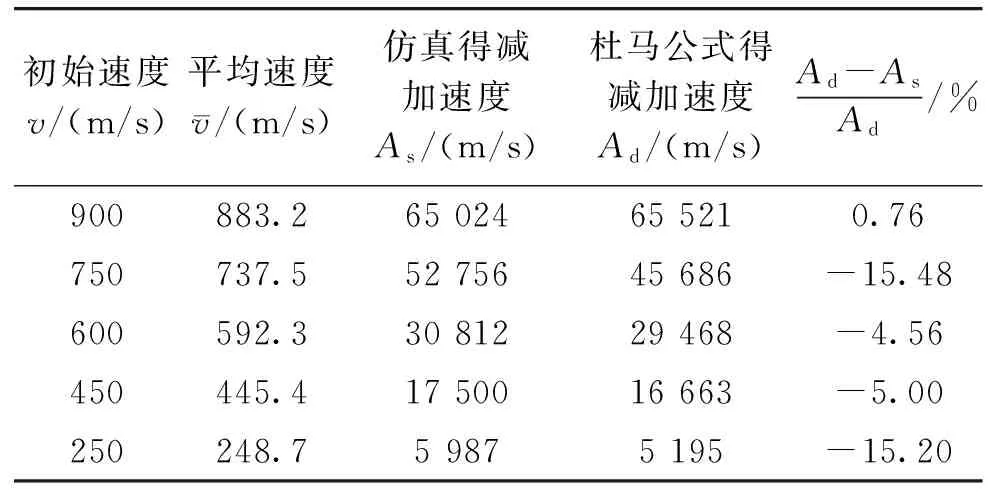
表4 仿真所得平均减加速度As与杜马经验公式所求减加速度Ad对比
4 结束语
文中基于ANSYS/LS-DYNA对76.2 mm口径舰炮弹丸以不同落角、不同落速侵入水中的冲击过程进行数值仿真分析,分析得到以下结论:
a)弹丸在15°及以上落角时,前冲过载峰值出现在弹顶圆台刚好完全没入水中的时刻,依落角和落速不同而分布在757g到13 456g之间,峰值宽度处于10 μs量级,峰值宽度随速度的增大呈减小趋势。
b)弹丸在5°和10°落角时,弹丸的速度方向变化明显,弹丸姿态不稳定,会发生跳弹现象。前冲过载峰值依落角和落速不同而分布在287g到7 150g之间,峰值宽度处于1 ms量级,峰值宽度随速度的增大呈减小趋势。
c)弹丸前冲过载值随落水速度增大而增大,并近似呈指数级关系增长;前冲过载也随落角增大而增大,并近似呈线性关系增长。
d)30°及以上落角入水时,径向过载相对于前冲过载较小,可忽略;小落角入水时,前冲过载峰值时刻径向过载较大,该径向过载有可能使惯性发火机构轴向运动摩擦增大,使其失效。
e)同一落角不同落速,径向过载与轴向过载相对变化趋势相同,但幅值不同。落速越高,幅值越高。
f)在5°落角下,仍有一个0.5~2 ms左右的时间窗口,在该时间窗口内,轴向过载大于径向过载所产生的摩擦作用,引信惯性机构仍能正确发火。但该窗口并不一定是在前冲过载初始时刻出现。
g)落速250 m/s、落角5°时,弹丸入水前冲过载峰值约为287g,其峰值持续时间约为2 ms。该过载是引信惯性发火机构发火正确性设计要考虑的可信极限弹道环境。
h)弹丸入水冲击峰值一般均出现在弹丸入水后100 μs之内,极个别在200 μs之内。因而引信惯性发火时间为惯性发火机构响应时间加上弹丸入水冲击峰值出现时间和爆炸序列作用时间。
i)仿真研究弹丸入水冲击产生的前冲过载,可不考虑弹丸自转及由此产生的马格努斯力的影响。
[1] 马庆鹏. 高速射弹入水过程多相流场特性研究 [D]. 哈尔滨: 哈尔滨工业大学, 2014.
[2] 孙凯, 党建军, 郝维敏, 等. 回转体超音速入水冲击数值仿真 [J]. 鱼雷技术, 2015, 23(1): 2-6.
[3] 王勇, 杨兴满. 空投沉底航行体入水和触底过程仿真研究 [J]. 科技创新与生产力, 2014(10): 92-94.
[4] 刘雨, 王雨时, 闻泉. 子弹垂直入水冲击过载数值仿真方法 [J]. 探测与控制学报, 2015, 37(1): 64-71.
[5] 初文华. 结构入水冲击过程三维数值模拟及实验验证 [J]. 舰船科学技术, 2015, 37(3): 21-27.
[6] 张苏, 古彪, 曹东风, 等. 基于ALE算法的V形楔形体入水的水动力特性分析 [J]. 固体力学学报, 2014, 35(S1): 95-100.
[7] 张红松, 胡仁喜, 康士延. ANSYS 14.5/LS-DYNA非线性有限元分析实例指导教程 [M]. 北京: 机械工业出版社, 2013: 355-356.
[8] 李裕春, 时党勇, 赵远. ANSYS 11. 0 LS-DYNA基础理论与工程实践 [M]. 北京: 中国水利水电出版社, 2008: 235-236.
[9] 臧国才, 李树常. 弹箭空气动力学 [M]. 北京: 兵器工业出版社, 1984: 260-262.
[10] 兵器工业总公司. 引信工程设计手册: GJB/Z 135-2002 [S]. 北京: 总装备部军标出版发行部, 2003: 40-42.
The Water Entry Set Forward Overload of a Medium-caliber Naval Projectile Based on Simulation
DONG Shengpeng1,WANG Yushi1,LI Zuohua2,ZHANG Zhibiao1,WEN Quan1
(1 School of Mechanical Engineering, NUST, Nanjing 210094, China; 2 Liaoning Huaxing Electromechanical Co. Ltd, Liaoning Jinzhou 121017, China)
In order to design and evaluate the fuze’s inertial forward firing mechanism of a medium caliber naval shell when shooting at sea, with the help of the commercial software ANSYS/LS-DYNA, using the arbitrary Lagrangian-Eulerian method, the water entry process of projectile with different falling speed and different falling angles was simulated. The water entry set forward overload coefficient of the projectile under the conditions of different falling speed, angle and rotation were got. The greater the falling speed or the falling angle, the greater the set forward overload, the smaller the overload peak width. The attitude of projectile was unstable when it fell into the water with small angle, and ricochet easily occurred. The set forward overload of projectile was reduced or even disappeared, and larger radial overload was produced. Rotation of the projectile entering the water had little effect on set forward overload and it could be neglected. When the overload of fall velocity was 250 m/s, and the falling angle was 5 degrees, the confidence limiting ballistic environment for inertial firing mechanism of fuze which firing accuracy design must be considered, the peak value of set forward overload was about 287g, and the duration was about 1 ms.
naval gun projectile; simulation; ballistic environment; fuze; water entry impact; set forward overload
2016-05-19
董盛鹏(1991-),男,湖北荆州人,硕士研究生,研究方向:引信设计。
TJ432.2
A

