右逆二项式态及其量子特性

陶 宇,刘堂昆

(湖北师范大学物理与电子科学学院，湖北 黄石 435002)

右逆二项式态及其量子特性

陶 宇,刘堂昆

(湖北师范大学物理与电子科学学院，湖北 黄石 435002)

用右逆算符在光场二项式态上重复作用m次，制备了一个新的光场量子态—右逆二项式态，并讨论了该光场态的非经典特性。

右逆算符；二项式态；右逆二项式态；量子特性

0 引言

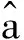
1 右逆二项式态的定义：

1985年，Stoler D 等人[4]引入了光场的二项式态(binomial state)：

(1)

而

(2)

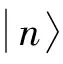
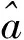
(3)

(4)

这个结果在1993年被范洪义[13]给出了严格的证明。

(5)

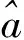
(6)

则

(7)

其中

(8)

又因为

(9)

所以

(10)

因此，右逆二项式态的数学表达式可以表示为：

(11)

2 右逆二项式态的非经典特性

2.1 平均光子数和光子数均方差：

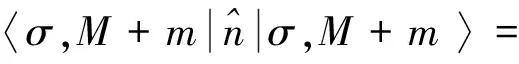
(12)

(13)

因此有

(14)

方差与平均值的比(相对起伏)由Fano因子给出

(15)

可见F=1-σ<1(相干态光场的F=1，光场呈泊松分布)，这就表明了右逆二项式态光场也呈现亚泊松分布(sub-Poissonian distribution)。

2.2 光子数分布函数和反聚束效应

(16)

其光子数分布函数为：

(17)

该式结果表明pn(σ，M+m)趋向于泊松分布。

(18)

2.3 坐标和动量的涨落(压缩效应)

已知坐标和动量的涨落分别为：

(19)

(20)

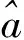
(21)

(22)

则

(23)

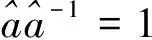
(24)

则有

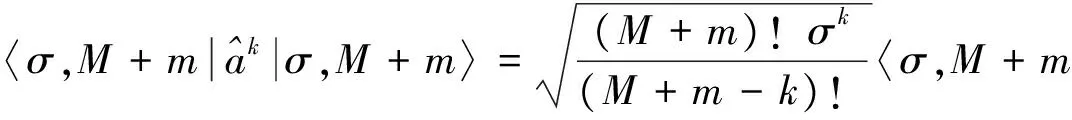
(25)

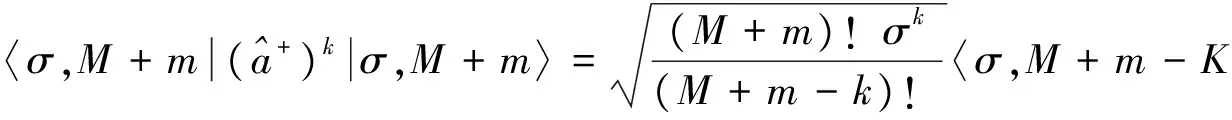
(26)

其中

〈σ，M+m‖σ，M+m-k〉=

(27)

由式(25)和(26)，可见

(28)

(29)

故有

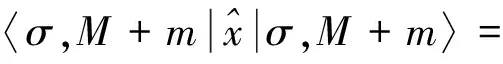
(30)

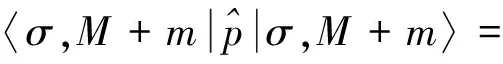
(31)

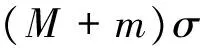
(32)

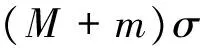
(33)

则有

(34)

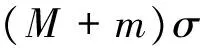
(35)

3 小结

我们采用右逆算符在光场二项式态上重复作用m次的方法，理论上制备了一个新的光场量子态，并称之为右逆二项式态，讨论了该光场态的非经典特性。研究结果表明：右逆二项式光场态是一个介于Fock态和Glauber态之间的中间态，呈现亚泊松分布和光子反聚束效应、坐标和动量压缩效应，而且与重复作用次数m有关。这个结果有助于原子与光场相互作用领域的研究工作。

[1]Agarwal G S, Tara K. Nonclassical properties of states generated by the excitations on a coherent state[J]. Phys Rev A, 1991, 43(1):492～497.

[2]Wei L F, Wang S J, Jie Q L. Excited states of coherent state and their nonclasscal properties[J]. Chin Sci Bull, 1997, 42(20):1686～1688.

[3]Nehta C L, Roy A K, Saxena G M. Eigenstates of two-photon annihilation operators[J]. Phys Rev A ,1992, 46(3):1565～1572.

[4]Stoler D, Saleh B E A, Teich M C. Binomial states of the quantized radiation field[J]. Opt Acta,1985, 32:345～355.

[5]Dattoli G, Galarde J, Torre A. Binomal state of the quantioned radiation field comment [J]. 1987, J Opt Soc Am, B2:185～191.

[6]Joshi A, Lawande S V. Properties of squeezed binomial states and squeezed negative binomial states [J]. 1991, J Mod Opt, 38(10):2009～2022.

[7]王晓光,于荣金,李 文. 位移二项式态与负位移二项式态的性质及其与二能级原子的相互作用[J]. 物理学报,1998,47(11):1798～06.

[8]Jiao Zhi-yong, Ma Jun-mao, Shang Yong-tao, et al. Quantum statistical properties of Binomial field interacting with two entangled atoms[J]. 2008, Commun. Theor. Phys. (Chinese) 50:971～973.

[9]姜道来,任学藻,丛红璐,等. 二项式光场与二能级原子相互作用的量子特性[J]. 中国科学,2010,40(2):201～206.

[10]范洪义,吴 泽. 二项-负二项组合光场态的光子统计性质及其在量子扩散通道中的生成[J].物理学报, 2015,64(8):080303～07.

[11]Liu Tang-kun , Tao Yu. Quantum Correlation of Two Entangled Atoms Interacting with the Binomial Optical Field[J]. J Theor Phys,2016, 55(6): 3047～3058.

[12]Mehta C L, Roy Anil K, Saxena G M. Eigenstates of two-photon annihilation operators[J]. Phys Rev A,1992，46(3):1565～1572.

[13]Fan Hong-yi. Inverse operators in Fock space studied via a coherent-state approach[J].Phys Rev A,1993,47(5): 4521～4523.

Right-inverse binomial state and their quantum properties

TAO Yu,LIU Tang-kun

(College of Physics and Electronic Science, Hubei Normal University, Huangshi 435002, China)

The m-times by the right-inverse operator acts on the optical field binomial state, we obtained a new quantum state (or called right-inverse binomial state), and discussed the nonclassical properties of the right-inverse binomial state.

right-inverse operator; binomial state; right-inverse binomial state; quantum properties

2016—11—10

陶宇(1993— )，男，湖北武穴市人，在读研究生;刘堂昆(1956— )，男，湖北武穴市人，博士，教授.

O413.1

A

2096-3149(2017)02- 0048-05

10.3969/j.issn.2096-3149.2017.02.011