基于滑模变结构的永磁同步电机伺服系统速度控制技术
郑再平,包婷萍,侍 威,贾淑绒,黄玉平
(北京精密机电控制设备研究所,北京,100076)
基于滑模变结构的永磁同步电机伺服系统速度控制技术
郑再平,包婷萍,侍 威,贾淑绒,黄玉平
(北京精密机电控制设备研究所,北京,100076)
速度环是永磁同步电机伺服系统三环控制的中间环节,其控制方法和控制技术的优劣直接影响整个系统的动态响应。根据永磁同步电机空间矢量图及矢量控制原理,分析永磁同步电机数学模型和动静态坐标变换方程,由于速度环的比例、积分(Proportion Integral,PI)控制存在速度超调、速度差积分饱和及抗扰动性能差等问题,提出基于滑模变结构的速度环控制方法,设计滑模面及切换函数,构建滑模变结构速度闭环控制器。分析电流环对电机反电势的影响,提出在电流环的设计过程中加入反电势补偿环节的电流控制器,并对电流环进行简化处理。利用仿真软件对系统电流环、速度环及系统进行建模,通过仿真研究,验证系统速度控制策略的可行性。
永磁同步电机;滑模变结构;速度调节器
0 引 言
永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)具有输出力矩大、功率密度高、可靠性好等优点,广泛应用于高精密航天机电伺服系统。在位置伺服控制中,永磁同步电机伺服驱动一般具有3个闭环控制环节,最外环的位置环作为伺服作动器位置定位控制环节,中间环节为速度控制环,最内环为电流控制环。速度环接收位置环输出,控制电流环的给定电流,其动态响应特性直接关系到矢量控制策略的实现,影响整个系统的动态性能。文献[1]应用有限元分析理论得到电感参数的变化,应用系统状态变量(绝对速度误差)抑制抖动,提高效率,提出了较比例、积分(Proportion Integral,PI)控制器更优异的算法控制转速,文献[2]提出一种新型的滑模趋近律(Sliding Mode Reaching Law,SMRL),这种SMRL可以动态地适应控制系统允许减少控制输入的同时保持控制器的高跟踪性能,然后用扩展滑模观测集中估计不确定性,弥补强干扰,达到高精度的目的;文献[3]提出了一种新型的永磁同步电机速度控制器,该控制器结合线性二次调节,采用积分变结构控制,使系统稳定;文献[4]引入自适应控制方案代替传统的永磁同步电机控制技术,通过观察摩擦和负载转矩实现精确的速度跟踪;文献[5]研究了永磁同步电机在考虑加速度情况下控制技术,文中应用表面式永磁同步电机(Surface Permanent Magnet Synchronous Motor,SPMSM),d轴电流是零控制;文献[6]介绍了一种并联滑模控制和模糊神经控制器的混合控制器,它是由并联连接的滑模控制器和模糊神经网络控制的永磁同步电机驱动器构成的速度控制;文献[7]提出了神经网络滑模自适应控制方法,并给出基于该方法的抗饱和方案,该方法引入PI控制,有效解决了神经网络局部收敛的问题;文献[8]提出了基于神经网络的自适应速度控制策略,运用神经网络算法对电流内环控制器的PI参数进行优化,速度外环采用滑模控制,实现了非线性系统的在线速度调整。
本文在分析永磁同步电动机空间矢量坐标原理基础上,推导永磁同步电机数学模型和坐标变换。由于速度环的PI控制存在速度超调、速度差积分饱和及抗扰动性能差等问题,提出基于滑模变结构的速度环控制方法,构建滑模变结构速度闭环控制器,设计滑模面及切换函数。根据电流环与脉宽调制(Pulse Width Modulation,PWM)关系,研究电流环对电机反电势的影响,提出在电流环的设计过程中加入反电势补偿环节的电流控制方法,并对电流环进行简化处理。系统地采用id=0的控制方法,利用仿真软件对系统建模和仿真分析,分析永磁同步电机在采用滑模变结构速度控制策略下额定转速空载运行、负载运行及变负载运行的工作状态,验证系统建模及速度环控制策略实现高性能工作的可行性。
1 永磁同步电机坐标变换
永磁同步电机的矢量控制需要对永磁同步电机内部矢量进行分析,通过一系列坐标变换,把电机三相电流、电压转换为直流电机两相坐标系进行控制,实现电机的解耦控制,绕组电流的输出直接控制电机输出电磁转矩。
永磁同步电机的矢量控制需要用到2种坐标系,静止-α β坐标系和动态-d q坐标系。图1为PMSM各坐标系关系。在图1中,在-α β坐标系下三相绕组ABC为空间相隔120°对称分布,A相绕组的矢量方向与-α β的α相一致,β相与α相互为90°。静态坐标变换将三相绕组的空间量转换为-α β直角坐标下的α、β相矢量。以α轴为公共参考坐标轴,设置三角坐标角度为0°,三相绕组为逆时针方向分布,β轴超前α轴90°。静态坐标变换后的iα和iβ分别代表电机三相电流在直角坐标系下的电流空间矢量。-d q轴坐标系是一个旋转的动态直角坐标系,其中,di和qi的数值量对应iα和iβ,在空间上相差电机转子旋转的电角度。因此,为了简化数学模型需要对转子位置角解耦,必须建立在-d q坐标系中。
根据永磁同步电机空间矢量图,通过三角函数关系在-α β坐标系中进行换算,三相绕组电压和电流量通过坐标变换得到直角分量uα,uβ,iα和iβ,它们可以代替永磁同步电机绕组电压和电流,物理意义一致,如图1所示,变换关系如下:
坐标变换以保证变换前后电机输出功率不变为前提,三相绕组的输出总功率等于两相绕组输出总功率,两相电机绕组的相电压是三相电机绕组相电压的倍。同时,两相电机绕组的相电流是三相绕组电机相电流的倍。这样直角坐标中的两相绕组每相功率增大了1.5倍,如果要保证两相电机的气隙合成磁势不变,两相绕组的匝数应发生相应变化。
电流矢量i在α- β静止坐标系中与α轴夹角为λ,d- q旋转坐标系与α- β坐标系之间的夹角θ。动态坐标变换的作用是把α- β坐标系表示的电流变换成d- q坐标系中带转子角度的电流矢量表示。由于i与d轴夹角为(λ-θ),相当于在α- β坐标系中把i逆时针旋转θ角,
如图1所示Park变换如下:
其逆变换又称为Park反变换:
2 滑模变结构控制器设计
传统永磁同步电机控制中的速度环普遍采用PI控制,PI控制策略通过对误差的现在与过去进行合理的加权可以实现对电机电流与速度的有效控制。但由于该控制策略采用误差的比例与积分的线性组合方式,使得控制变量存在快速性与超调的矛盾问题。PI控制策略中的误差积分项在消除控制系统静态误差的同时也会给系统带来不稳定因素,也可能引起积分饱和现象的发生。同时,在伺服系统中经常存在外部扰动,包括转动惯量及负载转矩突变等,如果不能对扰动进行合理的抑制与处理,整个控制系统的性能将会受到一定影响。
滑模变结构控制是一种利用跟踪轨迹和状态量切换相结合的控制方法,系统根据给定的运动轨迹使控制器的输出量沿轨迹运行,其控制特征为在跟踪轨迹同时利用一种特定的控制开关,迫使系统在一定条件下系统状态轨迹作小幅度、高频率的上下运动,这种运动称为滑模运动。该控制方法只是针对控制对象,与控制参数和扰动无关,具有很好的鲁棒性。
系统采用状态量进行闭环控制开关函数设计,如图2所示,控制函数U是状态变量x的函数,它包括2个极性相反的函数,ux+()和ux-(),该函数决定状态轨迹高频滑动切换幅值,系统总体控制结构在滑模控制中保持不变。但在滑模变结构控制系统中,总体切换函数u x()在整个反馈控制过程中为状态变量的非连续切换函数u x(),控制规律和切换函数s x()相结合共同控制u x()采用ux+()或ux-()的切换规律。
采用滑模变结构控制方式,切换函数为s(x),其控制函数为u(x)为
式中 u+(x)≠u-(x)。
取切换函数s( x)=cx1+x2,且c>0,为了保证滑模运动的可达性条件,则满足:
由此可知系统运动轨迹中s( x)=cx1+x2=0为滑模面。系统进入滑模面后,开始在滑模面邻域滑动,做高速开关切换运动,最终趋近于s˙=0并且s=0。
对于永磁同步电机采用id=0的定向矢量控制,电压方程为
利用前面给出的二阶系统的滑模变结构控制的设计方法对系统的速度调节器进行设计。零状态变量x=ω*-ω,x==-dω/dt=-,并且令输出量为
1
r2r u=,忽略粘滞系数B,根据基于id=0转子磁场定向矢量控制的原理可知PMSM系统状态方程。
对于速度环滑模控制器,取状态变量:
式中*ω为给定转速;rω为反馈转速。
结合上述方程可得:
得到系统状态空间方程为
设计滑模面:
选取控制规律:
其中:
参考滑模运动的可达性条件0ss<˙,解得:
为了削弱抖动,加入积分环节,将开关信号转为平稳的转矩信号,得到控制器的模型,如图3所示。
3 电流环参数设计
系统采用滑模变结构速度控制能较好地解决PI控制中存在的速度超调、速度差积分饱和及抗扰动性能差等问题,其输出为电流环的电流给定。作为内环的电流环控制,其动态响应直接影响控制系统的频率响应和系统动态性能。因此研究滑模变结构速度控制的同时,设计优越的电流环控制器对系统整体性能的提高尤为重要。
不同于速度环,电流环一般只与PWM逆变器和电机的参数相关,与外部负载的变换无关,因此电流环参数可以按照固定的方法计算。根据工程一般的设计思想,速度环计算周期为电流环计算周期的10倍左右,为此,电流环响应速度远大于速度环,在设计电流环控制器时可以忽略电机转子速度的变化,也就是说在电流环控制中认为电机的反电势保持不变。将电流环的控制模型简化为如图4所示。
其中,电机驱动环节可等效为一阶惯性环节,Kv与调制比相关的参数,通常调制比取1,TPWM=1/2fΔ,fΔ为三角波载波频率,通常情况下为5~20 kHz。
从图4可看出,控制过程虽简化了反电势变化的影响,但其反电势的幅值依然按参数控制计算,电流控制输出的其中一部分将对反电势进行抵消,这种反电势抵消计算过程必然会增加电压的调整时间,因此会降低速度的响应时间。为此,在电流环的设计过程中往往加入反电势补偿环节。通常调制比vK=1,因此加入反电势补偿后电流环控制系统,如图5所示。
通常情况下,控制器的载波周期很小,一个周期内可以认为反电势幅值不变,因此可以将反电势进行直接补偿,其补偿环节加在电流控制器之后,简化后的控制结构如图6所示。
从图6中可知,电流环的控制对象为:PWM逆变器、电枢回路。PWM逆变器可被看成具有时间常数TPWM=1/2fΔ的一阶惯性环节。本文涉及的伺服系统永磁同步电机的机械时间常数远大于电磁时间常数,可以将电机的模型等效为一阶惯性环节,如图7所示。
电流环中交轴和直轴PI控制器相同,传递函数为
由图7可以得出系统的开环传递函数为
利用工程中的设计方法,将上述传递函数设计为典型I型系统,即:
式(16)可以简化为
按照工程设计方法,对于典型I型系统,通常要求相角裕度为45o左右,阻尼比ζ=0.707,超调量为4.3%左右,参数设计如下:
由于三角波的载波频率较高,工程上可以忽略时间常数较大的惯性环节因素的影响,简化分析过程,因此可以将电流环的传递函数模型化简为
从式(20)可以看出,电流环经过简化等效为一阶惯性环节。
4 永磁同步电机控制系统仿真分析
系统采用id=0的控制方法,永磁同步电动机伺服系统如图8所示。电机参数选择,选取的电机参数如表1所示。
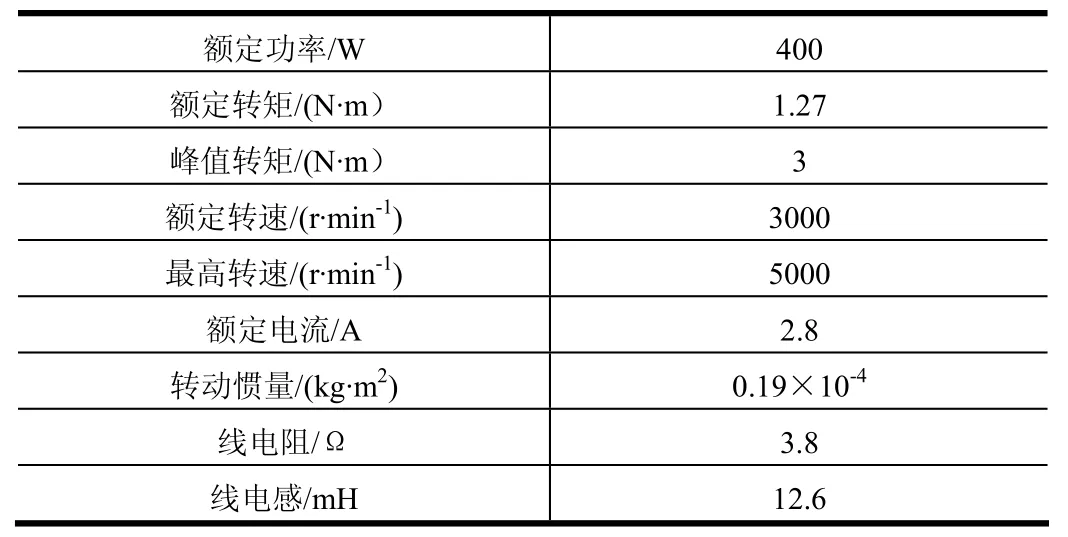
表1 永磁同步电机参数
速度控制器的输入为转子给定速度与实际速度反馈的差值,输出为q轴的电流指令为。对永磁同步电机三相电流进行检测并通过坐标变换得到实际的id,iq。速度控制器输出的电流指令,与实际电流id,iq比较,得到电流误差信号Δid,Δiq。电流误差信号通过电流调节器计算得到电压指令信号,,电压指令根据坐标变换得到三相PWM信号,对电压源逆变器的开关进行控制,使电机按照指令进行工作。
a)速度给定-1 500~1 500 r/min仿真分析。
速度给定-1 500~1 500 r/min的仿真结果如图9~12所示。
从图9~12可知,电机进入-1 500 r/min稳定转动后,突然施加反方向速度指令,绕组电流能迅速响应,4个PWM周期达到给定值,电机能迅速达到新的指定速度平稳运转,速度响应时间0.015 s,电流经过短暂的波动后也重新达到稳定状态。
b)突变负载3 N·m仿真分析。
突变负载3 N·m的仿真结果如图13~16所示。
前期研究表明,未加滑模变结构控制时,采用传统PI控制,系统无法实现3 N·m的负载突变情况。而采用滑模变结构控制后,当突变负载较大,超过额定负载时,由于滑模控制器的调节作用,系统转速仍然能快速回归给定值,系统鲁棒性较好,抗干扰能力强。
通过分析滑模变结构方法设计的速度环控制仿真结果,可以得出,采用滑模变结构控制的输出速度响应能较好地跟随输入信号,相比传统PI控制方法具有对系统参数变化不敏感,抗干扰能力强的优点。采用滑模变结构控制方法设计速度环控制器有效提高了PMSM位置伺服系统的鲁棒性,并且进一步提高了系统的动态响应能力。
5 结束语
机电伺服系统中主要有3个控制闭环,即位置环、速度环和电流环,其中电流闭环是系统的最内环,速度环为中间环节。其中速度环影响整个系统的动态性能和系统稳定性。本文提出了基于滑模变结构的速度环控制方法,构建了滑模变结构速度闭环控制器,设计了滑模面及切换函数。探讨了电流环对电机反电势的影响,研究了在电流环中加入反电势补偿环节的电流控制方法。利用仿真软件对系统进行建模,分析永磁同步电机在采用滑模变结构速度控制策略下额定转速空载运行、负载运行及变负载运行的工作状态及性能表征。研究表明,永磁同步电机采用滑模变结构速度闭环控制器,电流环加入反电势补偿环节能有效提高伺服系统的动态响应。
[1] Aimeng W. A new exponential reaching law of sliding mode control to improve performance of permanent magnet synchronous motor[J]. IEEE Transactions on Magnetics, 2013, 49(5): 2409-2412.
[2] Xiaoguang Zhang. Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation techniques[J]. IEEE Transactions on Power Electronics, 2013, 28(3): 1358-1365.
[3] Zaky M S. Adaptive switching plane of integral variable structure control for speed control of permanent magnet synchronous motor drives[J]. Electric Power Components and Systems, 2011, 39(13): 1353-1372.
[4] Chaoui H, Sicard P. Adaptive control of permanent magnet synchronous machines with disturbance estimation[J]. Control Theory Appl, 2012, 10(3): 337-343.
[5] Shin S, Choi C, Youm J, Lee T. Position control of PMSM using jerk-limited trajectory for torque ripple reduction in robot applications[C]. Montreal: 38th Annual Conference on IEEE Industrial Electronics Society, 2012.
[6] Elmas C, Ustun O. A hybrid controller for the speed control of a permanent magnet synchronous motor drive[J]. Control Engineering Practice 2008, 16(3): 260-270.
[7] 楚远征, 郭强强, 等. 永磁同步电机的新型滑模抗饱和控制研究[J]. 电机与控制应用, 2016(09): 38-43.
[8] 程辉, 杨克立, 等. 采用神经网络滑模控制的PMSM速度控制策略[J].河南工程学院学报, 2016(03): 47-50.
Speed Control Technology of Permanent Magnet Synchronous Motor Servo System Based on Sliding Mode Variable Structure
Zheng Zai-ping, Bao Ting-ping, Shi Wei, Jia Shu-rong, Huang Yu-ping
(Beijing Research Institute of Precise Mechatronic and Controls, Beijing, 100076)
The speed loop is an intermediate link of the three-ring control method that within the permanent magnet synchronous motor servo system, the control method and control technology of the speed loop directly affect the dynamic response of the whole system. According to the space vector diagram and the vector control theory of permanent magnet synchronous motor, the mathematical model of the motor and the dynamic and static coordinate transformation equation are analyzed. There are some problems about speed overshoot, velocity difference integral saturation and anti-disturbance energy difference in the PI control of the speed loop. The speed loop control method based on the sliding mode variable structure is proposed. In the meantime, the sliding mode surface and switching function are designed and then the sliding mode variable structure speed closed loop controller is constructed. By means of analyzing the influence of the current loop on the back electromotive force of the motor, the current controller based on the back EMF compensation link is put forward in the design of the current loop, after that the current loop could be implified. Through the modeling and simulation analysis of the system current loop, the speed loop and the whole system, the feasibility of the speed loop control strategy can be verified.
Permanent magnet synchronous motor; Sliding mode variable structure; Speed regulator
TP273
A
1004-7182(2017)03-0074-06
10.7654/j.issn.1004-7182.20170316
2016-12-19;
2017-03-01
郑再平(1979-),男,高级工程师,主要研究方向为机电伺服系统控制技术

