基于空间双曲交会的GNSS伪距单点定位算法

王 琰，张传定，车通宇

(1．信息工程大学 地理空间信息学院，河南 郑州 450052；2．北京卫星导航中心，北京 100094)

基于空间双曲交会的GNSS伪距单点定位算法

王 琰1,2，张传定2，车通宇1

(1．信息工程大学 地理空间信息学院，河南 郑州 450052；2．北京卫星导航中心，北京 100094)

针对GNSS卫星导航中的伪距单点定位，提出一种不需要测站坐标近似值的非迭代算法。该算法将GNSS伪距导航定位方程转化为空间双曲定位方程，给出具体的解算步骤，研究了空间双曲定位方程的解(有两解)，利用GNSS伪距导航定位的特点可消除多值性，从而实现无初值GNSS伪距单点定位。该算法与Bancroft算法相比，通过星间单差，与测站有关的公共误差项被消去，提高了定位精度；与传统的迭代算法相比，提高了计算效率，而且不需要测站坐标初值。最后通过IGS监测站实测数据对3种算法进行比较，验证了算法的有效性。

GNSS伪距导航;单点定位;空间双曲定位

GNSS伪距导航定位是任何型号GNSS接收机所必须具备的基本功能之一。当前解算单站接收机位置，常用的算法是基于传统的泰勒级数展开，将观测方程线性化后，组建法方程，通过不断迭代，参数收敛后获得最终的接收机位置。传统算法若不知道接收机位置的近似值，迭代搜索的收敛速度有时候较慢。该算法不可避免的问题是法方程求逆，因此该算法一般耗时较长[1-2]。对于地面连续运行监测站的近似坐标可以较为精确地获取，但是对于动态的测站，例如LEO，一般很难精确地知道其近似坐标，因此，研究无初值GNSS伪距快速导航定位有重要意义。

1985年Bancroft提出一种称为“闭合求解”的全局性非线性最小二乘算法(Bancroft算法)[3-4]，这是一种不需要迭代、具有代数解析性的直接解算方法，在计算上有效且数值稳定。该算法不需要点位位置作为迭代演算的初始值，主要依据R4维空间下的一种Lorentz内积，将原始伪距观测方程转化为一个一元二次方程求解问题。但是Bancroft算法存在问题，由于无法知道测站坐标的初值，因而与坐标有关的各种改正(对流层，相对论效应等)无法准确改正，因此，Bancroft算法最终组建的一元二次方程的系数会有误差，最终解算的测站位置误差较大。

国内外对于GNSS伪距单点定位的算法进行了详细研究。吕汉峰针对伪距单点定位解算中存在的两种定位模型的最小二乘解,给出了它们关于位置估计和定位精度等价性的推证过程。描述了伪距单点定位所采用的基本定位模型和单差定位模型，依据伪距观测值精度和单差基准分3种情况分别证明了两种模型的位置最小二乘解和定位精度是等价的[5]。吴传利用几何方法，给出了二维、三维测距定位问题解的解析表达式，在此解析解的基础上对GPS测码伪距定位问题提出一种趋近计算方法，并讨论了其收敛性[6]。Lloyd O.Krause提出了一种计算中矩阵最高阶2×2的非线性GPS导航定位方程[7]。P.S.NOE提出了一种适用于低成本GPS接收机的导航算法并进行了数据验证[8]。Abel J S验证了GPS伪距导航定位中模糊度无法固定的几种特殊情况下的算法[9]。Kleusberg A提出了在GPS伪距导航定位中的一种不需要线性化的直接解法并验证了单解、多解等多种特例[10]。廖华对线性最小二乘法、非线性最小二乘法、格网搜索法、kleus法等GPS伪距单点定位算法的基本原理及程序实现步骤进行了阐述,并从算法的可靠性、准确性及作业效率等方面进行了比较[11]。李鹤峰等以GPS为例，详细介绍伪距单点定位原理及解算模型,并给出了伪距单点定位程序实现中的关键点和易于出错之处的详细解决思路[12]。Oszczak B分析了GNSS标准定位中解算坐标和接收机钟差的基本原则、计算方程和矩阵偏微分算法，并进行了仿真的数值分析[13]。

大部分学者目前只是针对已有的算法进行程序实现或者性能比较，本文利用空间双曲交会定位原理提出一种新的算法，取一颗基准星，其他星的观测量与参考星组单差，一些与测站有关的误差项被消去，然后利用空间解析几何关系，将星间单差观测方程转换为空间双曲定位方程，详细推导了该算法的计算公式，并通过IGS监测站静态实测数据检验了算法的有效性。

1 GNSS伪距导航原理

如式(1)所示，GNSS伪距测量的基本观测方程为

(1)

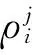
图1 GNSS伪距导航原理

众所周知，在无线电导航和定位中，有两种主要的方法：距离定位和距离差定位。有时把它们称为圆定位和双曲定位。从方程(1)可以看出，GNSS伪距导航在消除钟差dti后，将构成空间双曲定位方程。目前，平面、球面和椭球面双曲定位已有比较成熟的解法，而对于空间双曲定位仅限于特殊图形的解法[1]。因而，尽管可由空间双曲定位无初值解算测站点的地心坐标，但由于GNSS伪距导航图形分布的任意性，仍需研究任意图形下空间双曲定位的解算方法。

2 空间双曲定位解算

若选用S1为参考星，则消除钟差dti后，得方程组

(2)

其中符号的意义与式(1)一致。该方程组的左端隐含了测站i位置，右端为测站i到卫星j的距离差，最终构成空间双曲定位方程

(3)

下面利用余弦定理和解析几何知识，研究方程组(2)的解。在三角形Δj1i中，由余弦定理得

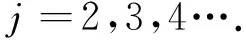
(4)

式中

(5)

是第j颗卫星到参考星的距离，可由卫星的坐标计算得出。将式(4)化简得

(6)

再由解析几何知识可以写出

(7)

将式(7)代入式(6)，并写成矩阵的形式，有

(8)

式中:

式(8)两边左乘AT，得

(9)

令N=ATA,U′=ATU,W′=ATW。

(10)

从而有

(11)

式中：

由一元二次方程根与系数的关系得

(12)

(13)

由上式所求得的解有两个，这是由双曲定位方程所决定的。在实际工作中，必须舍弃一个不符实际意义的解。对于海洋无线电定位而言，可用测站的近似高程来判断。对于GNSS伪距导航定位而言，符合实际意义的解可由钟差的范围或测站的近似向径来做出判断。但最佳的判断方案应为：若同时观测到4颗以上的卫星，则可以选取不同的基准星，可以得到两组或两组以上的解，再根据GNSS导航的精度，即可比较得出正确的解。若仅能观测到4颗卫星，则利用相临历元的两组解，也可比较得出正确的解(每组解中，正确的解随时间变化较小，不符实际意义的解随时间和卫星的运动变化较大)。

3 GNSS伪距导航无初值解算

由GNSS伪距观测量，选择适当的参考星，组成单差伪距观测量，即距离差观测量。依据星历文件计算观测时刻卫星的位置，并按式(5)到式(13)求出测站的可能解，按第2节所述的方法选取正确的解，从而确定出测站坐标的近似坐标和近似钟差。

为了验证本文算法的有效性，收集了2014年年积日072天IGS监测站AIRA站的数据进行试验，该测站位于日本北纬31.82°，东经130.6°，搭载TRIMBLE NETR9型接收机，天线类型是TRM59800.00 SCIS，能够同时接收GPS/GLONASS/QZSS三大系统的信号，采样间隔30 s，为了便于试验说明，仅采用GPS单系统的数据，图2显示了AIRA站在1～1 500历元接收到的GPS卫星个数和GDOP情况。从图2中可以看出该测站能观测到的卫星个数平均为8颗，而且不少于6颗，完全可以通过选取不同卫星的组合来判断双曲定位方程两个根的取舍。

图2 AIRA站1～1 500历元观测到的卫星个数和GDOP

分别采用3种算法进行定位试验，以下试验在ThinkPad T440p (CPU:Intel Core i7,主频:2.50 GHz,内存8 GB)笔记本计算机进行，其中传统的迭代算法在本文中设定迭代3次，3种算法的计算时间比较结果见表 1。

表1 3种算法的计算时间 s

3种算法的定位结果比较如图3～图5所示。

图3 Bancroft算法定位结果

3种算法的均值和RMS比较结果如表2所示，从结果可以明显看出，Bancroft算法的定位结果是最差的，本文提出的算法与传统的迭代算法的定位精度相当，但是达到同样的精度，计算效率却提高了约3.5倍。

图4 空间双曲定位算法定位结果

图5 传统迭代算法定位结果

项目XYZMEANRMSMEANRMSMEANRMSBancroft-41.656108.79311.097119.93222.78196.080双曲定位算法-30.73438.5072.10916.55715.75021.450迭代算法-1.9042.0651.0451.1911.3341.367

4 结 论

本文研究表明：不需要测站和卫星钟与接收机钟的钟差近似值,也可由空间双曲定位方程实现GNSS伪距导航解算。实测数据解算结果表明，本文提出的双曲定位算法最终定位精度比Bancroft算法的定位精度高，与传统的迭代算法定位精度相近，效率却提高了3.5倍。但该方法有两解，即二值性。消除二值性的方法有：

若仅有一个历元的4颗卫星的伪距观测值，则可按钟差的有效范围来判断，消除二值性；也可按测站的近似向径(地面站的近似向径为地球的平均半径)来判断，消除二值性。

若同时观测到4颗以上的卫星的伪距观测值，可以选取不同的基准星，得到两组或两组以上的解，再根据GNSS导航的精度，即可比较得出正确的解。

若观测到4颗卫星多个历元的伪距观测值，则利用相临历元的两组的解，也可比较得出正确的解(每组解中，正确的解随时间变化较小，不符实际意义的解随时间和卫星的运动变化较大，通常表现为地心向径较大)。

本文所提出的解算方法，仅为提供GNSS伪距导航的初值时使用。

[1] SEEBER G.Satellite Geodesy:Foundations,Methods,and Applications [M].Walter de Gruyter,1993,Berlin,New York.

[2] 许其凤.GPS卫星导航与定位[M].北京：解放军出版社，1988.

[3] BANCROFT S.An algebraic solution of the GPS equations.IEEE Trans.Aerosp.and Elec.Systems,1985,21(7),56-59.

[4] YANG Ming,CHEN Kuo-Hwa.Performance Assessment of a Noniterative Algorithm for Global Positioning System (GPS) Absolute Positioning[J].Proc.Natl.Sci.Counc.ROC(A) Vol.25,No.2,2001.pp.102-106.

[5] 吕汉峰,吴杰,张良.两种伪距单点定位模型最小二乘解的等价性证明[J].国防科技大学学报,2014,36(1):34-40.

[6] 吴传利,孙尧,李洪瑞.基于解析解的GPS伪距量测定位趋近算法[J].船舶工程,2006,28(1):41-45.

[7] KRAUSE O K.A direct solution to the GPS-type navigation equations [J].IEEE Trans,1987,AES-23(2):225-232.

[8] NOE P S.A navigation algorithm for low cost GPS receiver [J].Navigation,1978,25(2):258-264.

[9] ABEL J S.Existence and uniqueness of GPS solutions [J].IEEE Trans,1991,AES-27(6):952-956.

[10] KLEUSBERG A.Analytical GPS navigation solution [J].In:Grafarend EW,Krumm FW,Schwarze VS (eds) Geodesy-The Challenge of the 3rd Millennium.Springer,Berlin Heidelberg,2003：93-96.

[11] 廖华.GPS伪距单点定位算法的综合比较[J].测绘科学,2011,36(1):20-28.

[12] 李鹤峰,党亚民，王世进，等.GPS伪距单点定位程序实现若干问题[J].全球定位系统,2013,38(2):33-37.

[13] OSZCZAK B.GNSS positioning algorithms using methods of reference point indicators[J].Artif Satell,2014,49(1):21-32.

[责任编辑：刘文霞]

GNSS pseudo-range single point positioning algorithm based on space hyperbolic intersection

WANG Yan1,2,ZHANG Chuanding2,CHE Tongyu1

(1.School of Surveying and Mapping,Information Engineering University,Zhengzhou 450052,China;2.Beijing Global Information Application and Development Center,Beijing 100094,China)

A non-iterative algorithm is proposed, which does not require initial approximate value of the receiver’s position for GNSS pseudo-range single point positioning.In this algorithm,the GNSS pseudo-range positioning equation is transformed into space hyperbolic equation.The steps of calculation are discussed in this paper.The solutions of the space hyperbolic equation are analyzed.The characteristics of GNSS pseudo-range navigation and positioning can be used to judge the true value.Because all the common errors can be eliminated through the single differences between satellites,the accuracy of this algorithm is better than that of Bancroft algorithm.Compared with the iterative algorithm,the computational efficiency of this algorithm is improved and needs no initial approximate value of the receiver’s position.This algorithm proves to be effective through the IGS measurement data processing.

GNSS pseudo-range navigation;single point positioning;space hyperbolic positioning

著录：王琰，张传定，车通宇.基于空间双曲交会的GNSS伪距单点定位算法[J].测绘工程，2017，26(7)：16-21.

10.19349/j.cnki.issn1006-7949.2017.07.004

2016-07-10

国家自然科学基金资助项目(41374038,41174026)

王 琰(1990-)，男，博士研究生.

P228

A

1006-7949(2017)07-0016-06