有机半导体的电子电离能、亲和势和极化能的密度泛函理论研究
郭姿含 胡竹斌 孙真荣 孙海涛
(华东师范大学精密光谱科学与技术国家重点实验室,物理与材料科学学院,上海 200062)
有机半导体的电子电离能、亲和势和极化能的密度泛函理论研究
郭姿含 胡竹斌 孙真荣 孙海涛*
(华东师范大学精密光谱科学与技术国家重点实验室,物理与材料科学学院,上海 200062)
准确预测有机半导体的能级(如电子电离能和亲和势等)对设计新型有机半导体材料和理解相关机理至关重要。从理论计算的角度看,主要挑战来自于缺少一种不仅能够在定性上合理而且在定量上精确预测,同时并不显著增加计算成本的理论方法。本文中,我们证明了通过结合极化连续介质模型(PCM)和“最优调控”区间分离密度泛函方法能够准确预测一系列有机半导体的电子电离能(IP)、亲和势(EA)和极化能,其预测结果与实验数据吻合得很好。重要的是,经过调控后分子的前线分子轨道能量(即-εHOMO和-εLUMO)与对应的IP和EA计算值很接近。调控方法的成功可以进一步归因于其能够根据不同分子体系或同种分子所处的不同状态(气态和固态)“最优”地平衡泛函中分别用于描述电子局域化和离域化的作用。相比而言,其它常见的密度泛函方法由于包含的HF%比例过低(如PBE)或过高(如M06HF和未调控的区间分离泛函),均不能给予合理的预测。因此,我们相信这种PCM-调控的方法能够为研究其它更加复杂的有机体系的能级问题提供一种更加可靠和便捷的理论工具。
有机半导体;密度泛函理论;最优化调控;区间分离泛函;带隙
1 引 言
近年来,随着科学技术的不断发展和人们需求的不断提高,由有机半导体材料组成的电子通信产品逐步进入到我们的日常生活中,成为了我们日常生活中不可缺少的组成部分。相比传统半导体材料而言,有机半导体具有轻便、柔性好、生产成本低和器件制备方式灵活等优点,在新型显示与照明、新能源、信息传输与存储等领域显现出广阔的应用前景1-4。在有机半导体材料中,调节导带和价带的电子能级的高低以及带隙的大小,可以有效操控载流子(空穴和电子)运动的方式和路径,从而间接地决定了有机半导体的性质和用途5,6。例如,在由多层有机薄膜构成的有机发光二极管中,载流子的注入和传输通常发生在有机材料的价带最高能级和导带最低能级上。层与层界面处的能级高低决定着电子和空穴能否最终顺利进入发光层,形成激子并辐射能量进而发光7。因此,对有机半导体材料而言,能够精确地测量或预测上述的这些参数,进而进行能级的匹配,不仅有利于我们深入理解载流子注入和传输等机理,而且能够帮助实验工作者设计和筛选性能优异的备选材料。

图1 有机半导体分子在气态(左)和固态(右)下的前线分子轨道(HOMO和LUMO)能级以及电离能(IP)和亲和势(EA)的示意图Fig.1 Sketch of frontier molecular orbitals (HOMO and LUMO) and ionization potential (IP) and electron affinity (EA) of organic semiconductor molecules in gas phase (left) and solid state (right) Egrepresents the fundamental gap.
对有机半导体而言,分别与其价带和导带能级概念直接对应的描述有两种8,9,如图1所示,(1) 前线分子轨道,即最高占据轨道(HOMO)和最低空轨道(LUMO),它们之间的能量差就是轨道能隙(Δε = εHOMO- εLUMO);(2) 电子电离能(IP)与亲和势(EA),即体系失去或接受一个自由电子所需的能量,它们的能量差即基本带隙(Eg= IP -EA)。实验上的电离能和亲和势大小分别可以通过光电子能谱(ultraviolet photoemission spectroscopy (UPS)和inverse photoemission spectroscopy (IPES))或循环伏安法等手段测得10。然而,由不同的研究小组报道同种材料分子的IP和EA实验值有时会有明显的区别,导致这些测量值的物理解释依然充满争议11-13。通常来讲,以下几种因素可能会造成实验测量的不确定性:(1) 不同的数据采集和分析方式,如使用谱图的峰值或端值等;(2) 薄膜样品的形貌或结晶度不同;(3) 材料表界面的特征,因为光电子能谱等测试手段对表界面极度敏感;(4) 采用不同的基底会导致分子在基底表面不同的取向;(5) 不可控的环境和温度影响,以及样品表面的氧化变质等;(6) 设备仪器的分辨率等。基于此,在理论上发展一种既精确又高效的计算方法能够对有机半导体的各个能级参数进行准确预测将会显得尤其重要。
一方面,从物理概念上看,IP和HOMO具有直接对应的关系,于是我们希望通过计算得到的HOMO轨道能量可以直接用来表征或描述IP的大小,同样地,EA和LUMO也是类似。另一方面,基于格林函数(G)和屏蔽库仑作用(W)近似的多体微扰理论(MBPT)14,15和基于后-Hartree-Fock (PHF)16-18理论等高水平方法被证明可以准确预测有机分子体系的IP和EA等光谱性能参数。但是,这些高水平方法在处理较大尺寸分子或复杂体系时将会变得非常的昂贵,普通的计算能力将变得难以承受;此外,基于GW近似的非自洽方法的计算精度也非常依赖于其所采用的起点波函数的质量,这也为该方法的普及增加了难度。相比而言,密度泛函理论(DFT)由于可以极大地减少计算量,被广泛应用于描述从原子、分子到大尺寸团簇的电子结构19,20。然而,由于传统的密度泛函存在大的离域化误差(DE)或自作用误差(SIE)等因素21-25,利用这些传统的密度泛函计算的HOMO和LUMO轨道能量并不能很好地对应IP和EA的大小。例如,在描述孤立分子时,广义梯度近似(GGA)泛函(如PBE26)和部分杂化泛函(如B3LYP27,28)通常会高估HOMO能级并低估LUMO能级,导致得到的轨道带隙偏小。很多研究者利用上述这些泛函计算得到的气态下小分子的前线轨道能量和实验测得对应固态薄膜的IP和EA测量值进行比较,发现它们吻合的非常好。显而易见,这样偶然的吻合只能归因于误差抵消的结果,因为气态下的计算值根本没有考虑固态极化效应的影响,而这种极化效应在有机晶体或薄膜中是非常重要的12,29。
近年来,以色列科学家Baer和Kronik等人提出了一种对区间分离密度泛函的区间分离参数ω进行“最优调控”的概念30-32:在准确的Kohn-Sham (KS)DFT中,HOMO轨道能量的负值应该等于垂直电离能(vertical IP)31,即中性和阳离子体系的总能量差。利用这种IP-调控方法计算气态下有机小分子的前线轨道能量的精度能与高水平的GW方法相媲美,而计算成本显著降低。然而,Kronik等人指出上述的调控方法仅能适用于原子或小分子体系,而对于像分子晶体等周期性体系则无能为力33。其主要原因就是调控过程需要计算阳离子体系的能量,对于周期性体系来说,无法合理引入一个背景电荷。为了使这种调控方法也能用来描述固态体系,我们最近发展了一种结合连续极化介质模型(PCM)34,35和“最优调控”概念的方法36,37,进一步发现这种PCM-调控的方法能够准确预测一些有机分子晶体(如并五苯,红荧烯和C60衍生物等)的电离能和亲和势。
在本文中,考察了13种常见的有机半导体材料分子(如图2所示),这些材料分子中大多数被用于有机发光二极管器件的空穴或电子传输层。这里我们利用DFT分别计算了这些有机半导体在孤立分子和固态薄膜状态下的IP和EA(包括HOMO和LUMO能级大小),并与已有的实验值进行比较。结果发现PCM-调控方法能够精确地预测上述的能级参数,计算结果与实验值吻合得很好。由于兼顾较高的精度和较低的计算成本,相信基于PCM-调控的计算方法将来有望被用于其它更加广泛的有机半导体体系的性能预测。
2 计算方法
密度泛函理论计算的精度通常与具体泛函的选择密切相关,对于不同的体系或者同一体系的不同性质,存在不同的“最优”泛函近似,使得传统的密度泛函不具有普遍预测性。比如在构建杂化密度泛函时,通常会在“纯”GGA泛函基础上通过杂化部分比例的非定域准确交换项(eX%或HF%),如B3LYP (20%HF)、BMK (42%HF)38、M06-2X (54%HF)39、M06-HF (100%HF)40等。然而不同杂化泛函中HF%的含量是固定的,对于不同的体系往往需要不同含量的HF%,因此无法用统一的杂化泛函来描述。针对这个问题,区间分离密度泛函的发展为调控最优的HF%含量提供了理论框架,其表达式可以由误差函数erf(x)和电子间距离r12具体表达为:

其中泛函的交换项进一步被分隔为短程处类似DFT的交换项和长程处类似HF的准确交换项。方程中的ω为区间分离参数,其物理意义为泛函的交换项主要由类似DFT为主转变为类似HF为主的电子间距离的倒数。一方面,由于区间分离密度泛函中默认的ω参数值在实际计算时往往并不具有最优的表现41;另一方面,由于ω本身是电子密度的函数42,不同的分子体系对应不同的最优ω值,因此对ω参数进行调控是有必要的。Baer和Kronik等人通过构造一个J方程使其能最大程度满足IP-调控准则:

即通过调节参数ω使得中性分子体系HOMO轨道能量的负值与对应的垂直电离能尽可能接近。为了能够更好地描述轨道能隙(即HOMO-LUMO gap),构造了另一个形式上更加完善的J2方程43:
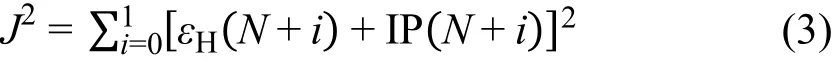
在忽略电子弛豫效应的前提下,我们将N + 1电子阴离子体系的电离能IP(N + 1)近似看成N电子体系的亲和能EA(N),这种通过最小化J2方程的方法被称为带隙调控(即GAP-调控)。这种带隙调控不仅可以使得所计算的负的HOMO轨道能量等于IP值,同时也能保证负的LUMO值接近EA值,即:
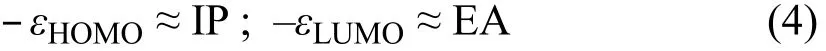
本文中我们将利用这种GAP-调控的方法来对有机半导体分子进行调控,进而计算孤立气态分子的电子能级;而在模拟固态极化作用时,我们则基于上面的调控模型,同时为了合理地模拟固态极化环境,我们借鉴极化连续介质模型(PCM),近似认为固态晶体或薄膜状态下的分子“溶解”在同种分子的溶剂中,这种考虑固态极化作用的调控称为PCM-调控。对应的介电常数可以通过求解Clausius-Mossotti方程44获得:其中,α和V分别是分子的静态各向同性极化率和分子体积。α和V的大小分别在B3LYP/6-31G(d)水平下计算,并利用Multiwfn程序45读取具体值并进行单位换算。最后将α和V值带入方程(5)计算出介电常数的大小(见表1)。本文中13种有机半导体材料分子均采用B3LYP泛函和6-31G(d)基组进行几何构型的全优化,所有计算都在Gaussian 0946软件下完成。
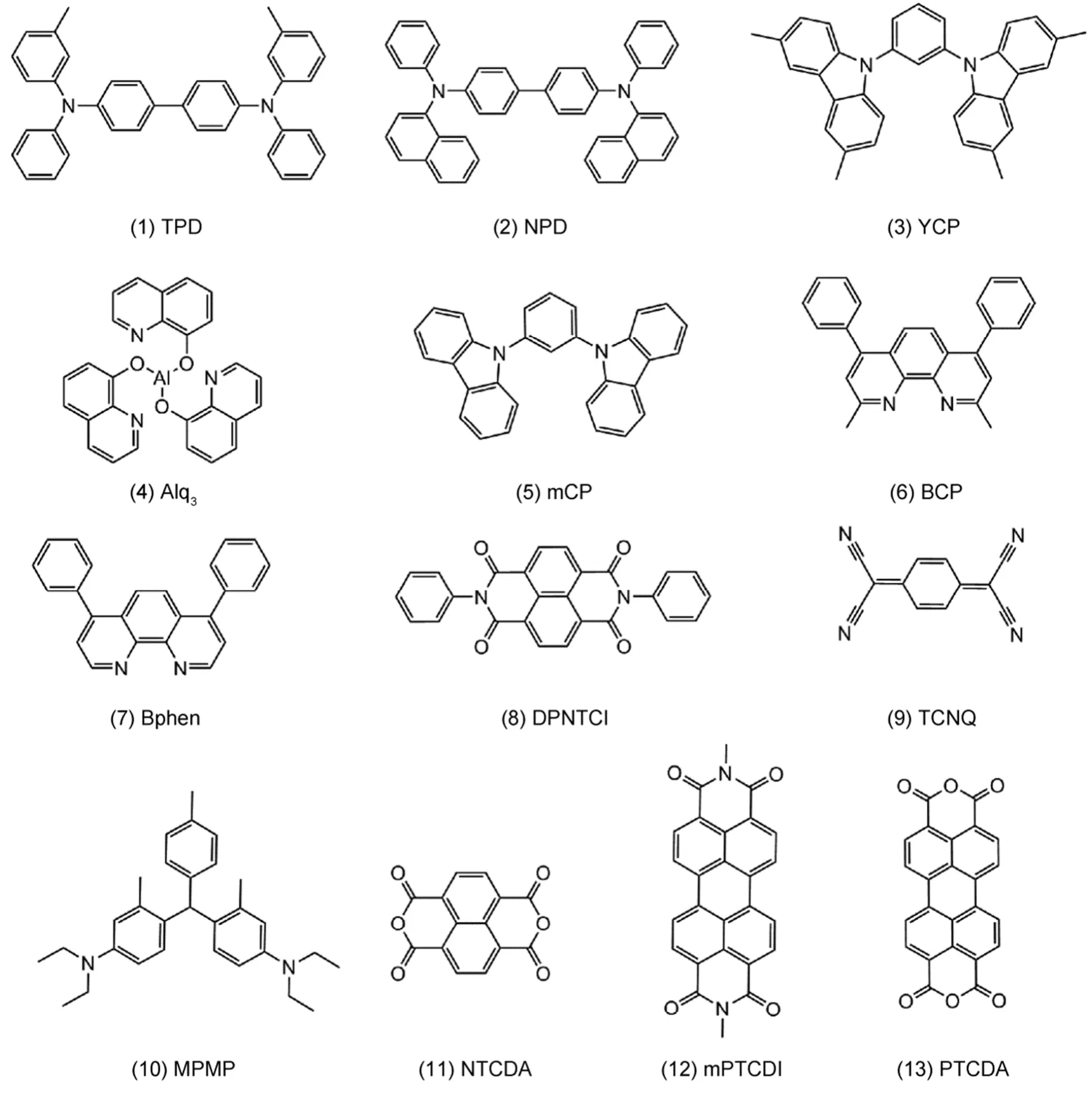
图2 本文中所计算的13种有机半导体分子Fig.2 13 organic semiconductor molecules calculated in this work

除HF以外,本文共考察了8种常见的密度泛函方法,包括PBE、B3LYP、BMK、M062X、M06HF、CAM-B3LYP47、LC-ωPBE48、ωB97XD49。我们选择LC-ωPBE泛函进行调控,把经过调控后的泛函标记为LC-ωPBE*。在优化后的有机半导体分子构型基础上,利用上面的各种泛函方法对HOMO和LUMO轨道能量,电子电离能和亲和势分别进行计算,并与已有的实验值进行比较。
3 结果与讨论
表1列出了由公式(5)计算得到的13种有机半导体材料的介电常数,大小范围介于2.7-4.2之间。对于气态分子,我们在LC-ωPBE泛函上沿用以前GAP-调控的方法。结果发现,与LC-ωPBE泛函的默认ω(= 0.40 bohr-1)相比,调控后的最优ω参数值显著降低到大约在0.17-0.25 bohr-1范围。然而,在PCM下引入介电常数进行调控后,其最优ω值进一步减小到0.04-0.08 bohr-1左右。我们知道ω是电子密度的函数,Körzdörfer等人也发现聚乙烯共轭长度越长,体系越离域,其对应的最优ω值越小,直至达到共轭极限42。因此,与气态孤立分子相比,较小的ω值可以解释为在固态极化作用下所对应的电子密度会变得更加离域,因此对应的最优ω值更小。从区间分离泛函的方程(1)角度考虑,较小的ω值意味着类似DFT的交换作用将会在较大的电子间距离处被类似HF的交换项所取代,这不难理解,因为在固态极化环境下需要泛函中包含更多能够描述电子离域特征的作用项。
经过调控程序以后,我们首先利用LC-ωPBE*泛函分别计算了13种有机半导体分子分别在气态和固态下的HOMO和LUMO轨道能量以及对应的IP和EA大小,如表2所示50-61。由于大多数材料分子的IP和EA值都是在薄膜或晶体下测得的,因此通过与已有的实验值进行比较,我们统计了相应的平均绝对误差(MAD)大小。由表2可以看出,经过PCM-调控后的LC-ωPBE*泛函能够使计算的-εHOMO和-εLUMO轨道能量值分别与对应的IP和EA计算值吻合得很好。其次,如表3所示,LC-ωPBE*泛函能够很好地预测实验的结果,与对应实验值相比,所计算的-εHOMO(IP)的MAD仅为0.28 eV(0.27 eV)以及-εLUMO(EA)的MAD为0.41 eV (0.40 eV)。此外,如图3所示,由LC-ωPBE*泛函计算的-εHOMO(IP)理论值与实验测量值具有很好的线性相关性,其线性相关系数R2分别为0.975(0.978)。为了更好地比较各种泛函方法在实际计算时的优劣,我们还考察了其它9种常见的方法,包括PBE(0%HF)、B3LYP(20%HF)、BMK(42%HF)、 M062X(54%HF)、M06HF(100%HF)、CAM-B3LYP (19%-65%HF)、LC-ωPBE(0-100%HF)、ωB97XD(22%-100%HF)和HF。为了考察所含不同比例HF%的影响,我们将各种方法所含的HF%比例标出。利用上述9种方法所计算的详细能级参数参见补充文件 (Supporting Information)中的表S1-S9。由于缺少足够的气态分子的实验数据,表3仅列出了与固态下IP和EA实验数据相比的各种泛函方法计算的MAD值。总体来讲,除了调控后的LC-ωPBE*泛函外,所有的泛函方法所预测的负的轨道能量(-εHOMO和-εLUMO)与对应的IP和EA计算值都存在不同程度的偏差。首先,我们先考察各种方法所计算的-εHOMO和-εLUMO在描述实验IP和EA测量值的表现。其中,PBE(0%HF)和M06HF(100%HF)泛函计算的误差明显高于B3LYP(20%HF)、BMK(42%HF)和M062X (54%HF)。前者(PBE)计算的-εHOMO低估了实验IP值(MAD = 1.09 eV),而计算的-εLUMO高估了实验EA值(MAD = 0.43 eV);后者(M06HF)则正好相反,表现为计算的-εHOMO高估了实验IP值(MAD = 2.44 eV),同时计算的-εLUMO低估了实验EA值(MAD = 1.93 eV)。在这些泛函中,B3LYP的预测最为可靠,其预测实验IP和EA测量值的MAD分别为0.41和0.27 eV。上述结果暗示了泛函中包含过低或过高的HF%都不利于准确描述实验结果,而具有适度的HF%比例则能够有效地减小误差。相比于上述传统的杂化泛函,未经过调控的区间分离泛函(CAM-B3LYP、LC-ωPBE和ωB97XD)计算的误差有所增加,这也暗示了泛函中默认的ω参数有进一步优化的必要。根据Koopmans理论,由HF计算的-εHOMO理论上应该接近于对应的垂直电离能计算值(即由HF计算的阳离子和中性体系的能量差),而实际上(由图4可见)这样的近似其实是很差的。由HF计算的-εHOMO高估了实验IP值(MAD = 1.57 eV),同时计算的-εLUMO严重低估了实验EA值(MAD = 3.42 eV)。因此,使用HF方法来预测有机半导体的带隙是极不可靠的。
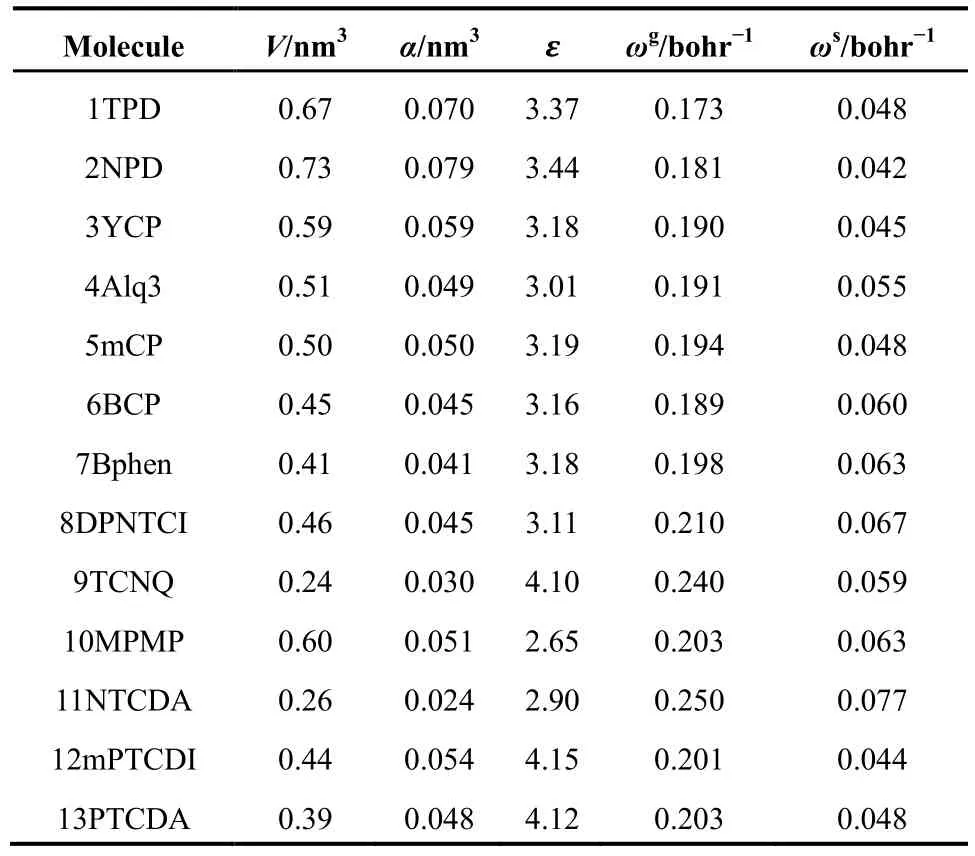
表1 在B3LYP/6-31G(d)水平下计算的13种有机半导体分子的分子体积V,静态极化率α和介电常数ε,以及在气态(g)和固态(s)下调控的最优ω参数值Table 1 Calculated volume of molecules V, static molecular polarizability α and dielectric constant ε at the B3LYP/6-31G(d) level, and optimally-tuned ω in gas phase (g) and solid state (s)
表2 在LC-ωPBE*/6-31G(d)水平下计算的固态和气态下各分子轨道能量和-、垂直电离能()、亲和势()以及由UPS和IPES测得的实验值(IPUPS和EAIPES)(其中上标s和g代表固态和气态)Table 2 Calculated orbital energies (), vertical ionization energies) and vertical electron affinitiesin solid state (s) and gas phase (g) at the LC-ωPBE*/6-31G(d) level and the experimental IPUPSand EAIPESvalues measured by UPS and IPES
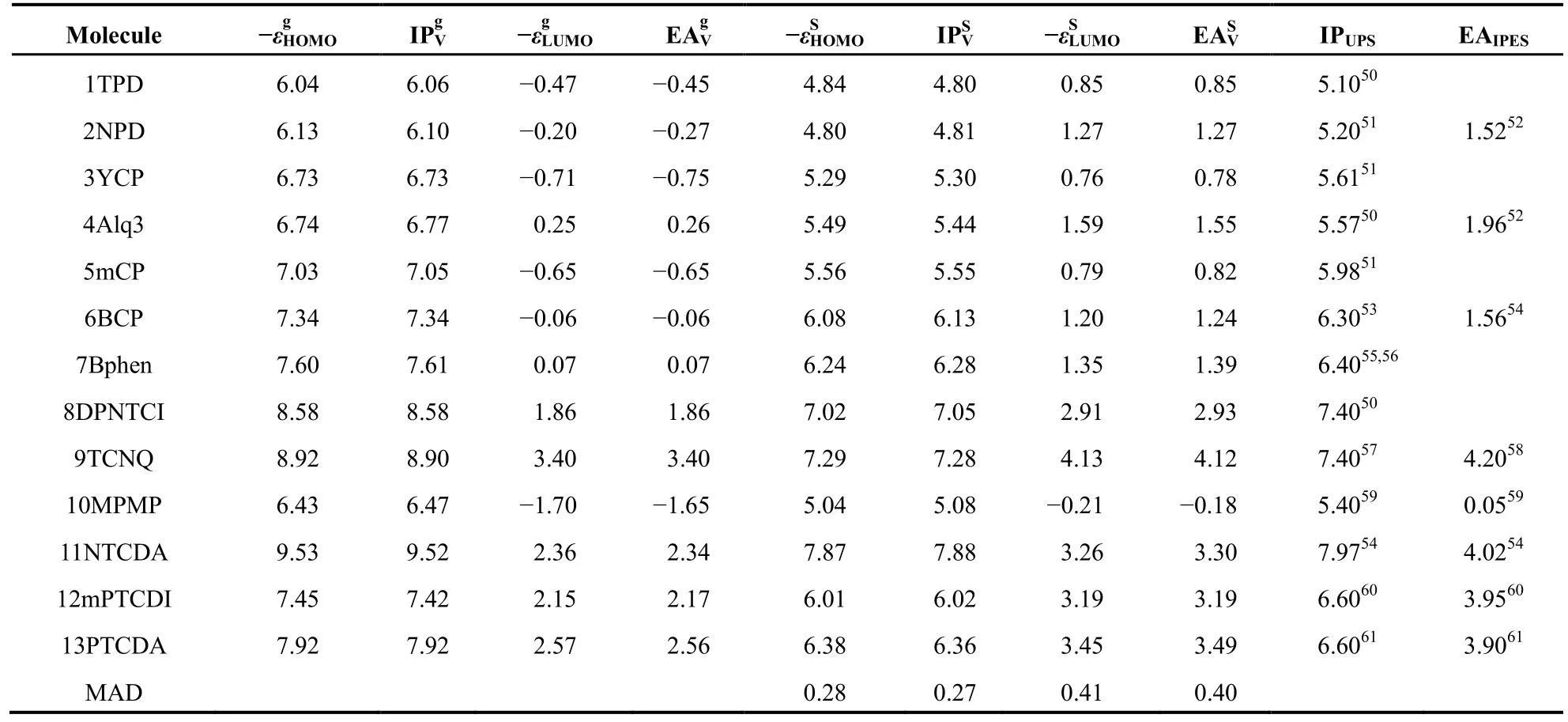
表2 在LC-ωPBE*/6-31G(d)水平下计算的固态和气态下各分子轨道能量和-、垂直电离能()、亲和势()以及由UPS和IPES测得的实验值(IPUPS和EAIPES)(其中上标s和g代表固态和气态)Table 2 Calculated orbital energies (), vertical ionization energies) and vertical electron affinitiesin solid state (s) and gas phase (g) at the LC-ωPBE*/6-31G(d) level and the experimental IPUPSand EAIPESvalues measured by UPS and IPES
All units are in eV.
Molecule -εgHOMOIPgV-εgLUMOEAgV-εSHOMOIPSV-εSLUMOEASVIPUPSEAIPES1TPD 6.04 6.06 -0.47 -0.45 4.84 4.80 0.85 0.85 5.10502NPD 6.13 6.10 -0.20 -0.27 4.80 4.81 1.27 1.27 5.20511.52523YCP 6.73 6.73 -0.71 -0.75 5.29 5.30 0.76 0.78 5.61514Alq3 6.74 6.77 0.25 0.26 5.49 5.44 1.59 1.55 5.57501.96525mCP 7.03 7.05 -0.65 -0.65 5.56 5.55 0.79 0.82 5.98516BCP 7.34 7.34 -0.06 -0.06 6.08 6.13 1.20 1.24 6.30531.56547Bphen 7.60 7.61 0.07 0.07 6.24 6.28 1.35 1.39 6.4055,568DPNTCI 8.58 8.58 1.86 1.86 7.02 7.05 2.91 2.93 7.40509TCNQ 8.92 8.90 3.40 3.40 7.29 7.28 4.13 4.12 7.40574.205810MPMP 6.43 6.47 -1.70 -1.65 5.04 5.08 -0.21 -0.18 5.40590.055911NTCDA 9.53 9.52 2.36 2.34 7.87 7.88 3.26 3.30 7.97544.025412mPTCDI 7.45 7.42 2.15 2.17 6.01 6.02 3.19 3.19 6.60603.956013PTCDA 7.92 7.92 2.57 2.56 6.38 6.36 3.45 3.49 6.60613.9061MAD 0.28 0.27 0.41 0.40
表3 各种密度泛函方法计算的固态下分子轨道能量()、垂直电离能()、亲和势()相对于实验值的平均绝对误差(MAD)aTable 3 Mean absolute deviation (MAD) of the calculated orbital energies (-and -), vertical ionization energies) and vertical electron affinities () in solid state using various density functionals compared to the experimental valuesa
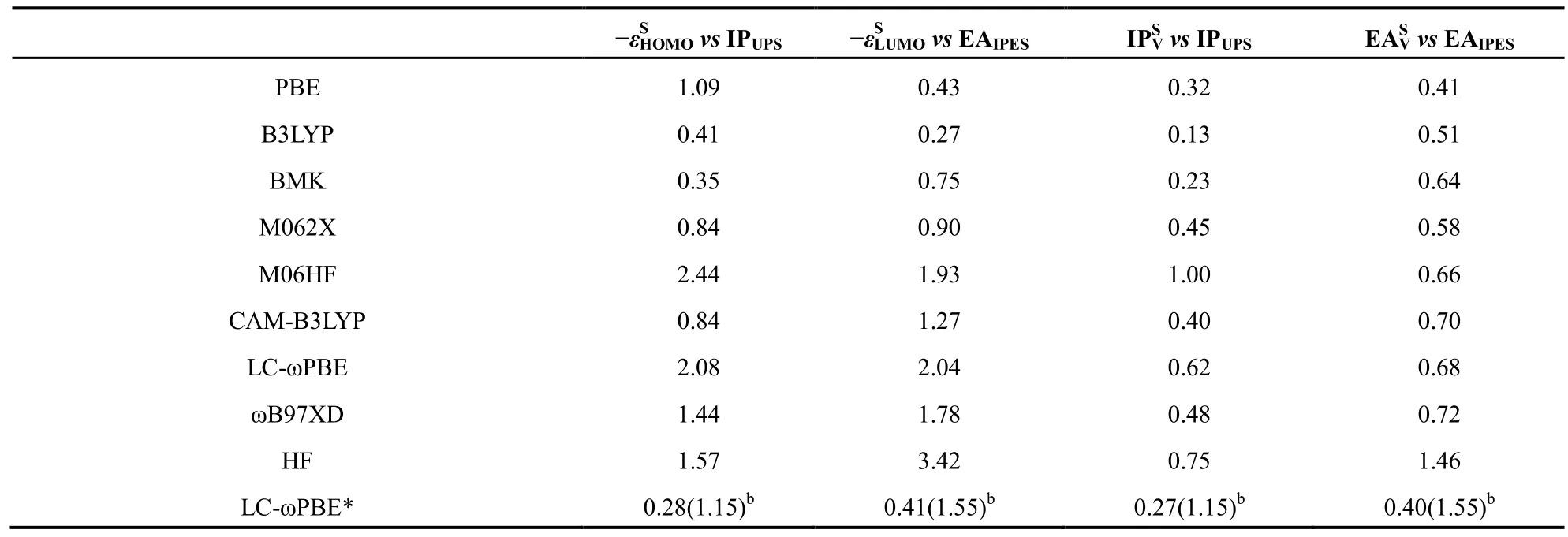
表3 各种密度泛函方法计算的固态下分子轨道能量()、垂直电离能()、亲和势()相对于实验值的平均绝对误差(MAD)aTable 3 Mean absolute deviation (MAD) of the calculated orbital energies (-and -), vertical ionization energies) and vertical electron affinities () in solid state using various density functionals compared to the experimental valuesa
aAll units are in eVs.bValues in parentheses are collected without PCM model.
-εSHOMOvs IPUPS-εSLUMOvs EAIPESIPSVvs IPUPSEASVvs EAIPESPBE 1.09 0.43 0.32 0.41 B3LYP 0.41 0.27 0.13 0.51 BMK 0.35 0.75 0.23 0.64 M062X 0.84 0.90 0.45 0.58 M06HF 2.44 1.93 1.00 0.66 CAM-B3LYP 0.84 1.27 0.40 0.70 LC-ωPBE 2.08 2.04 0.62 0.68 ωB97XD 1.44 1.78 0.48 0.72 HF 1.57 3.42 0.75 1.46 LC-ωPBE* 0.28(1.15)b0.41(1.55)b0.27(1.15)b0.40(1.55)b
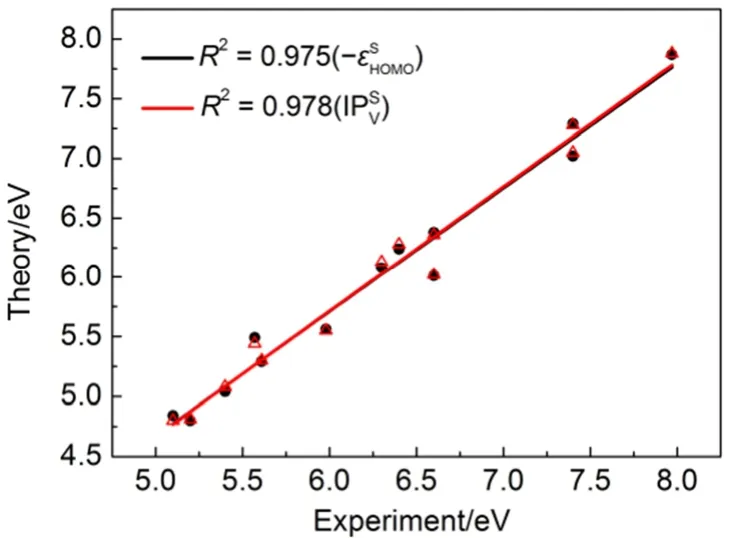
图3 在LC-ωPBE*/6-31G(d)水平下计算的13种分子在固态下分子轨道能量和电离能与实验值IPUPS的关系图Fig.3 Correlation of calculated orbital energiesand vertical ionization energiesusing LC-ωPBE*/6-31G(d) with experimental ionization energies IPUPSof 13 molecules in the solid state color online

图4 与实验值相比,各种密度泛函方法计算的(固态下)分子轨道能量(和)、垂直电离能()、亲和势()的平均绝对误差Fig.4 Mean absolute deviation (MAD) of the calculated orbital energies (and -), vertical ionization energies () and electron affinities () in the solid state using various density functionals compared to the available experimental values
接下来我们再比较计算的IP和EA理论值在描述实验IP和EA测量值时的表现。与上面计算的-εHOMO和-εLUMO相比,绝大多数泛函方法结合PCM模型后所计算的IP和EA值所对应的MAD都有明显减小。值得注意的是,在描述EA实验值时,HF所计算的MAD值很大,达到1.46 eV,主要是由于HF不包含电子关联作用。因此,在利用HF描述有机半导体的EA时需要格外注意。总之,经过PCM调控后的LC-ωPBE*泛函能够很好地预测实验结果,特别是能够很好地满足-εHOMO≈IP以及-εLUMO≈EA。
表4 各种密度泛函方法计算的气态下分子电子电离能与固态下电子电离能的差值, 即极化能P+(公式(6))Table 4 Calculated polarization energies (P+), defined as energy differences between the calculatedin gas phase andin the solid state, see equation (6)
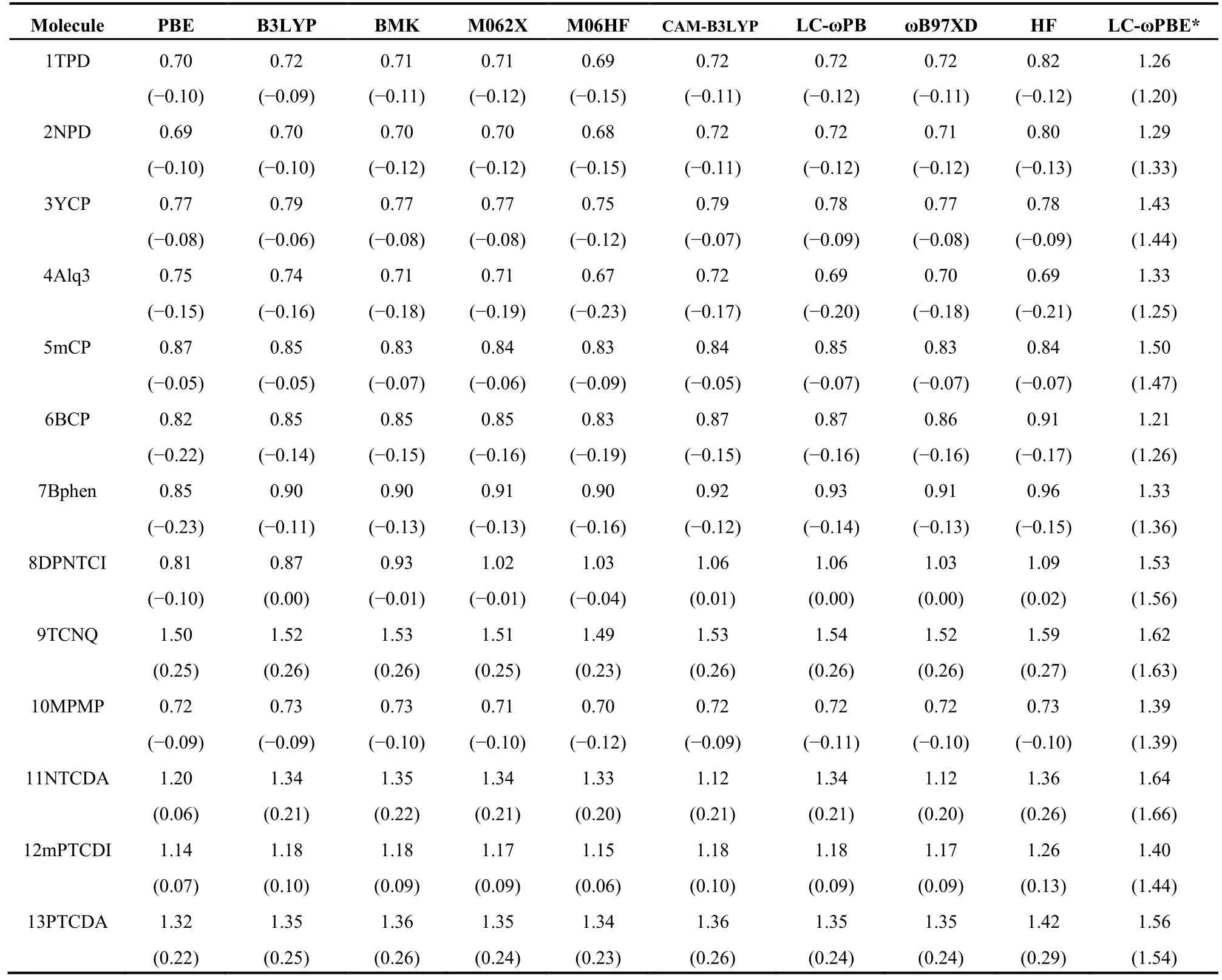
表4 各种密度泛函方法计算的气态下分子电子电离能与固态下电子电离能的差值, 即极化能P+(公式(6))Table 4 Calculated polarization energies (P+), defined as energy differences between the calculatedin gas phase andin the solid state, see equation (6)
All units are in eVs. The energy differences between the calculated orbital energies as shown in parentheses, see equation (7).
Molecule PBE B3LYP BMK M062X M06HF CAM-B3LYP LC-ωPBωB97XD HF LC-ωPBE* 1TPD 0.70 0.72 0.71 0.71 0.69 0.72 0.72 0.72 0.82 1.26 (-0.10) (-0.09) (-0.11) (-0.12) (-0.15) (-0.11) (-0.12) (-0.11) (-0.12) (1.20) 2NPD 0.69 0.70 0.70 0.70 0.68 0.72 0.72 0.71 0.80 1.29 (-0.10) (-0.10) (-0.12) (-0.12) (-0.15) (-0.11) (-0.12) (-0.12) (-0.13) (1.33) 3YCP 0.77 0.79 0.77 0.77 0.75 0.79 0.78 0.77 0.78 1.43 (-0.08) (-0.06) (-0.08) (-0.08) (-0.12) (-0.07) (-0.09) (-0.08) (-0.09) (1.44) 4Alq3 0.75 0.74 0.71 0.71 0.67 0.72 0.69 0.70 0.69 1.33 (-0.15) (-0.16) (-0.18) (-0.19) (-0.23) (-0.17) (-0.20) (-0.18) (-0.21) (1.25) 5mCP 0.87 0.85 0.83 0.84 0.83 0.84 0.85 0.83 0.84 1.50 (-0.05) (-0.05) (-0.07) (-0.06) (-0.09) (-0.05) (-0.07) (-0.07) (-0.07) (1.47) 6BCP 0.82 0.85 0.85 0.85 0.83 0.87 0.87 0.86 0.91 1.21 (-0.22) (-0.14) (-0.15) (-0.16) (-0.19) (-0.15) (-0.16) (-0.16) (-0.17) (1.26) 7Bphen 0.85 0.90 0.90 0.91 0.90 0.92 0.93 0.91 0.96 1.33 (-0.23) (-0.11) (-0.13) (-0.13) (-0.16) (-0.12) (-0.14) (-0.13) (-0.15) (1.36) 8DPNTCI 0.81 0.87 0.93 1.02 1.03 1.06 1.06 1.03 1.09 1.53 (-0.10) (0.00) (-0.01) (-0.01) (-0.04) (0.01) (0.00) (0.00) (0.02) (1.56) 9TCNQ 1.50 1.52 1.53 1.51 1.49 1.53 1.54 1.52 1.59 1.62 (0.25) (0.26) (0.26) (0.25) (0.23) (0.26) (0.26) (0.26) (0.27) (1.63) 10MPMP 0.72 0.73 0.73 0.71 0.70 0.72 0.72 0.72 0.73 1.39 (-0.09) (-0.09) (-0.10) (-0.10) (-0.12) (-0.09) (-0.11) (-0.10) (-0.10) (1.39) 11NTCDA 1.20 1.34 1.35 1.34 1.33 1.12 1.34 1.12 1.36 1.64 (0.06) (0.21) (0.22) (0.21) (0.20) (0.21) (0.21) (0.20) (0.26) (1.66) 12mPTCDI 1.14 1.18 1.18 1.17 1.15 1.18 1.18 1.17 1.26 1.40 (0.07) (0.10) (0.09) (0.09) (0.06) (0.10) (0.09) (0.09) (0.13) (1.44) 13PTCDA 1.32 1.35 1.36 1.35 1.34 1.36 1.35 1.35 1.42 1.56 (0.22) (0.25) (0.26) (0.24) (0.23) (0.26) (0.24) (0.24) (0.29) (1.54)
与气态下的孤立分子不同的是,有机晶体或无定形薄膜下的分子与分子通过弱的范德华分子间相互作用,它们会同时受到分子内和相邻分子的电子极化作用,而电子极化作用是有机半导体材料的一个非常重要的特征9,11。定量表征其极化能大小对理解有机分子晶体或无定形薄膜下的电荷传输性质非常重要。一般而言,极化能大小(P+)可以理解为带电体在静电环境作用下用来稳定正电荷所需要的能量大小。P+的大小可以由Lyons模型定义为一个分子分别在气态下和固态下的电子电离能(IP)的差,即

同样,我们也考察了对应的HOMO轨道的能量变化,即

如表4所示,我们利用上述10种密度泛函方法计算了材料的极化能大小P+。首先,如图1所示,由于极化作用的存在,固态下的IP值大小通常小于气态下的IP值。因此,由方程(6)定义下的P+表现为正值。我们发现所有的泛函计算的IPVg和IPVs的能量差都为正值,即都能够定性准确地描述极化能大小。由于缺少足够气态下的IP实验值,因此也无法给出P+的实验值。Sato等人通过光电子能谱测量了44种有机固体的P+,发现大多数多环芳烃化合物的P+都在1.7 eV左右57。本文中,LC-ωPBE*预测的13种有机材料的P+都在1.20-1.65 eV之间,与已有的实验值范围较为吻合,其它泛函计算的P+值都明显偏小。尤其值得注意的是,当利用方程(7)的轨道能级表征极化能大小时,除了调控后的LC-ωPBE*泛函能够对所有分子都提供定性准确的预测外,没有任何一种方法能够给予定性正确的预测,表现为绝大多数的极化能计算值为负值。利用调控方法成功预测P+值的原因主要是其能够同时对分子在气态和固态极化下的IP值大小进行准确预测,尤其是-εHOMO能够与IP匹配得很好。由上节可知,B3LYP虽然“巧合”能够预测固态下的IP值,但是对气态下的IP值则不能准确预测,因而对P+的预测也是失败的。
4 结 论
在本文中,我们证明了一种结合极化连续介质模型(PCM)和最优调控区间分离密度泛函(LC-ωPBE*)的理论方法的可靠性,这种方法能够准确预测一系列有机半导体材料分子的电子电离能和亲和势。与已有的实验测量值相比,计算得到的-εHOMO和IP的平均绝对误差(MAD)分别为0.28和0.27 eV,而计算的-εLUMO和EA的MAD分别为0.41和0.40 eV。尤其是,经过调控后的LC-ωPBE*泛函方法计算得到的前线分子轨道能量(-εHOMO和-εLUMO)分别与对应的IP和EA计算值非常接近。由于调控方法能够同时准确预测同种分子在气态和固态极化下的电离能大小,因而对应的极化能大小(即IPVg与IPVs的能量差)也能被很好地描述。调控方法的优势在于其能够根据不同分子所具有不同的电荷密度分布,对区间分离泛函的参数进行最优调控,最终能够合理平衡泛函中用于描述电子局域化和离域化的作用。相比而言,其它常见的密度泛函方法由于包含的HF%比例过低(如PBE)或过高(如M06HF和未调控的区间分离泛函),均不能给予合理的预测,具体表现为:PBE等泛函低估了IP并高估了EA,这类泛函对电荷分布的描述表现为过分离域化;而M06HF等则相反,这类方法则表现为过分局域化。对于极化能的计算,除了调控方法外,没有任何一种常见泛函能够给予定性准确的计算预测。
本项工作的一个创新之处,就是结合最优“调控”区间分离密度泛函理论方法62,63和极化连续介质模型来模拟固态极化屏蔽效应64,近似认为固态晶体或薄膜状态下的分子“溶解”在同种分子的溶剂中,以此基于单个分子并结合极化连续介质模型来模拟固体体系,这样处理的另一个优势就是实际计算成本更低,避免了对周期性体系的计算,计算结果也表明了这样近似处理是合理的,能够很好地重复实验的结果。然而,由于我们的当前模型的限制(即仅仅基于单个分子),结合极化连续介质模型(环境极化作用)来近似模拟分子晶体或薄膜的性质,减小计算成本的代价是没有充分考虑分子间的具体相互作用,例如,分子间电子耦合造成的能级劈裂问题,晶体或薄膜中具体的分子堆积形式以及在单晶中存在的各向异性等问题,目前的模型还没有充分考虑,接下来的工作包括对当前的理论模型进一步优化和完善。
基于调控方法的精度和便利性,我们相信这种结合PCM模型和最优调控区间分离泛函的理论方法将为研究更加广泛和更大尺寸的有机半导体材料提供一种可靠、高效的理论工具。Supporting Information: available free of charge via the internet at http://www.whxb.pku.edu.cn.
(1) Forrest, S. R.; Thompson, M. E. Chem. Rev. 2007, 107, 923. doi: 10.1021/cr0501590
(2) Heeger, A. J. Angew. Chem. 2001, 40, 2591. doi: 10.1002/1521-3773(20010716)40:14<2591::AIDANIE2591>3.0.CO;2-0
(3) Klauk, H. (Ed.) Organic Electronics, Materials, Manufacturing and Applications; Wiley-WCH, Weinheim, 2006; pp 411-418.
(4) Müllen, K.; Wegner, G. Electronic Materials: The Oligomer Approach; Wiley-VCH: 1998; pp 235-275.
(5) Brédas, J. L.; Calbert, J. P.; da Silva Filho, D. A.; Cornil, J. Pro. Natl. Acad. Sci. U. S. A. 2002, 99, 5804. doi: 10.1073/pnas.092143399
(6) Pope, M.; Swenberg, C. E.; Pope, M.; Swenberg, C. E. Electronic Processes in Organic Crystals and Polymers, 2nd ed.; Oxford Univ. Press: New York, 1999; Chapter 2.
(7) Tang, C. W.; VanSlyke, S. A. Appl. Phys. Lett. 1987, 51, 913. doi: 10.1063/1.98799
(9) Kahn, A. Mater. Horiz. 2016, 3, 7. doi: 10.1039/c5mh00160a
(10) Krause, S.; Casu, M. B.; Schöll, A.; Umbach, E. New J. Phys. 2008, 10, 085001. doi: 10.1088/1367-2630/10/8/085001
(11) Ryno, S. M.; Risko, C.; Bredas, J. L. J. Am. Chem. Soc. 2014, 136, 6421. doi: 10.1021/ja501725s
(12) Sharifzadeh, S.; Biller, A.; Kronik, L.; Neaton, J. B. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85, 125307. doi: 10.1103/PhysRevB.85.125307
(13) Heimel, G.; Salzmann, I.; Duhm, S.; Koch, N. Chem. Mater. 2011, 23, 359. doi: 10.1021/cm1021257
(14) Hedin, L. Phys. Rev. 1965, 139, A796. doi: 10.1103/PhysRev.139.A796
(15) Hybertsen, M. S.; Louie, S. G. Phys. Rev. B 1986, 34, 5390. doi: 10.1103/PhysRevB.34.5390
(16) Chen, L.; Zhu, L.; Shuai, Z. J. Phys. Chem. A 2006, 110, 13349. doi: 10.1021/jp0652998
(17) Fabiano, E.; Sala, F. D.; Cingolani, R.; Weimer, M.; Gorling, A. J. Phys. Chem. A 2005, 109, 3078. doi: 10.1021/jp044974f
(18) Hammond, J. R.; Kowalski, K. J. Chem. Phys. 2009, 130, 194108. doi: 10.1063/1.3134744
(19) Kohn, W.; Sham, L. J. Phys. Rev. 1965, 140, A1133. doi: 10.1103/PhysRev.140.A1133
(20) Seidl, A.; Görling, A.; Vogl, P.; Majewski, J. A.; Levy, M. Phys. Rev. B 1996, 53, 3764. doi: 10.1103/PhysRevB.53.3764
(21) Cohen, A. J.; Mori-Sánchez, P.; Yang, W. Science 2008, 321, 792. doi: 10.1126/science.1158722
(22) Körzdörfer, T.; Brédas, J. L. Acc. Chem. Res. 2014, 47, 3284. doi: 10.1021/ar500021t
(23) Zheng, X.; Li, C.; Zhang, D.; Yang, W. Sci. China Chem. 2015, 58, 1825. doi: 10.1007/s11426-015-5501-z
(24) Mori- Sánchez, P.; Cohen, A. J.; Yang, W. Phys. Rev. Lett. 2008, 100, 146401. doi: 10.1103/PhysRevLett.100.146401
(25) Perdew, J. P.; Zunger, A. Phys. Rev. B 1981, 23, 5048. doi: 10.1103/PhysRevB.23.5048
(26) Perdew, J. P.; Burke, K.; Ernzerhof, M. Phys. Rev. Lett. 1996, 77, 3865. doi: 10.1103/PhysRevLett.77.3865
(27) Becke, A. D. J. Chem. Phys. 1993, 98, 5648. doi: 10.1063/1.464913
(28) Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785. doi: 10.1103/PhysRevB.37.785
(29) Refaely-Abramson, S.; Sharifzadeh, S.; Jain, M.; Baer, R.; Neaton, J. B.; Kronik, L. Phys. Rev. B 2013, 88, 1336. doi: 10.1103/PhysRevB.88.081204
(30) Baer, R.; Livshits, E.; Salzner, U. Annu. Rev. Phys. Chem. 2010, 61, 85. doi: 10.1146/annurev.physchem.012809.103321
(31) Kleinman, L. Phys. Rev. B 1997, 56, 12042. doi: 10.1103/PhysRevB.56.12042
(32) Stein, T.; Kronik, L.; Baer, R. J. Chem. Phys. 2009, 131, 244119. doi: 10.1063/1.3269029
(33) Kronik, L.; Stein, T.; Refaely-Abramson, S.; Baer, R. J. Chem. Theory Comput. 2012, 8, 1515. doi: 10.1021/ct2009363
(34) Mennucci, B. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 386. doi: 10.1002/wcms.1086
(35) Tomasi, J.; Mennucci, B.; Cammi, R. Chem. Rev. 2005, 105, 2999. doi: 10.1021/cr9904009
(36) Sun, H.; Hu, Z.; Zhong, C.; Zhang, S.; Sun, Z. J. Phys. Chem. C 2016, 120, 8048. doi: 10.1021/acs.jpcc.6b01975
(37) Sun, H.; Ryno, S.; Zhong, C.; Ravva, M. K.; Sun, Z.; Körzdörfer, T.; Brédas, J. L. J. Chem. Theory Comput. 2016, 12, 2906. doi: 10.1021/acs.jctc.6b00225
(38) Boese, A. D.; Martin, J. M. J. Chem. Phys. 2004, 121, 3405. doi: 10.1063/1.1774975
(39) Zhao, Y.; Truhlar, D. G. Theor. Chem. Acc. 2008, 120, 215. doi: 10.1007/s00214-007-0310-x
(40) Zhao, Y.; Truhlar, D. G. J. Phys. Chem. A 2006, 110, 13126. doi: 10.1021/jp066479k
(41) Sun, H.; Autschbach, J. J. Chem. Theory Comput. 2014, 10, 1035. doi: 10.1021/ct4009975
(42) Körzdörfer, T.; Sears, J. S.; Sutton, C.; Brédas, J. L. J. Chem. Phys. 2011, 135, 204107. doi: 10.1063/1.3663856
(43) Stein, T.; Kronik, L.; Baer, R. J. Am. Chem. Soc. 2009, 131, 2818. doi: 10.1021/ja8087482
(44) Ashcroft, N. W.; Mermin, N. D. Solid State Physics;Holt, Rinehart and Winston, New York, 1978, 9, 33. doi: 10.1002/piuz.19780090109
(45) Lu, T.; Chen, F. J. Comput. Chem. 2012, 33, 580. doi: 10.1002/jcc.22885
(46) Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; et al. Gaussian 09, Revision A.01; Gaussian Inc.: Wallingford, CT, 2009.
(47) Yanai, T.; Tew, D. P.; Handy, N. C. Chem. Phys. Lett. 2004, 393, 51. doi: 10.1016/j.cplett.2004.06.011
(48) Vydrov, O. A.; Scuseria, G. E. J. Chem. Phys. 2006, 125, 234109. doi: 10.1063/1.2409292
(49) Chai, J. D.; Head-Gordon, M. J. Chem. Phys. 2008, 128, 084106. doi: 10.1063/1.2834918
(50) Sugiyama, K.; Yoshimura, D.; Miyamae, T.; Miyazaki, T. J. Appl. Phys. 1998, 83, 4928. doi: 10.1063/1.367309
(51) Dandrade, B.; Datta, S.; Forrest, S.; Djurovich, P.; Polikarpov, E.; Thompson, M. Org. Electron. 2005, 6, 11. doi: 10.1016/j.orgel.2005.01.002
(52) Hill, I. G.; Kahn, A.; Cornil, J.; dos Santos, D. A.; Brédas, J. L. Chem. Phys. Lett. 2000, 317, 444. doi: 10.1016/s0009-2614(99)01384-6
(53) Tang, J. X.; Zhou, Y. C.; Liu, Z. T.; Lee, C. S.; Lee, S. T. Appl. Phys. Lett. 2008, 93, 043512. doi: 10.1063/1.2966155
(54) Chan, C. K.; Kim, E. G.; Brédas, J. L.; Kahn, A. Adv. Funct. Mater. 2006, 16, 831. doi: 10.1002/adfm.200500402
(55) Chan, M. Y.; Lai, S. L.; Lau, K. M.; Lee, C. S.; Lee, S. T. Appl. Phys. Lett. 2006, 89, 163515. doi: 10.1063/1.2362974
(56) Pfeiffer, M.; Forrest, S. R.; Leo, K.; Thompson, M. E. Adv. Mater. 2002, 14, 1633. doi: 10.1002/1521-4095(20021118)14:22<1633::AID-ADMA1633>3.0.CO;2-#
(57) Sato, N.; Seki, K.; Inokuchi, H. J. Chem. Soc., Faraday Trans. 2 1981, 77, 1621. doi: 10.1039/f29817701621
(58) Kanai, K.; Akaike, K.; Koyasu, K.; Sakai, K.; Nishi, T.; Kamizuru, Y.; Nishi, T.; Ouchi, Y.; Seki, K. Appl. Phys. A 2008, 95, 309. doi: 10.1007/s00339-008-5021-1
(59) Wang, Y.; Gao, W.; Braun, S.; Salaneck, W. R.; Amy, F.; Chan, C.; Kahn, A. Appl. Phys. Lett. 2005, 87, 193501. doi: 10.1063/1.2117623
(60) Zahn, D. R. T.; Gavrila, G. N.; Gorgoi, M. Chem. Phys. 2006, 325, 99. doi: 10.1016/j.chemphys.2006.02.003
(61) Schwenn, P. E.; Burn, P. L.; Powell, B. J. Org. Electron. 2011, 12, 394. doi: 10.1016/j.orgel.2010.11.025
(62) Tian, X.; Sun, H.; Zhang, Q.; Chihaya, A. Chin. Chem. Lett. 2016, 27, 1445. doi: 10.1016/j.cclet.2016.07.017
(63) Sun, H.; Zhong, C.; Sun, Z. Acta Phys. -Chim. Sin. 2016, 32, 2197. [孙海涛, 钟 成, 孙真荣. 物理化学学报, 2016, 32, 2197.] doi: 10.3866/PKU.WHXB201605301
(64) Hu, Z.; Zhou, B.; Sun, Z.; Sun, H. J. Comput. Chem. 2017, 38, 569. doi: 10.1002/jcc.24736
Density Functional Theory Studies on Ionization Energies, Electron Affinities, and Polarization Energies of Organic Semiconductors
GUO Zi-Han HU Zhu-Bin SUN Zhen-Rong SUN Hai-Tao*
(State Key Laboratory of Precision Spectroscopy, and School of Physics and Materials Science, East China Normal University, Shanghai 200062, P. R. China)
Accurate prediction of the energy levels (i.e. ionization potential and electronic affinity) of organic semiconductors is essential for understanding related mechanisms and for designing novel organic semiconductor materials. From a theoretical point of view, a major challenge arises from the lack of a reliable method that can provide not only qualitative but also quantitative predictions at an acceptable computational cost. In this study, we demonstrate an approach, combining the polarizable continuum model (PCM) and the optimally tuned range-separated (RS) functional method, which provides the ionization potentials (IPs), electron affinities (EAs), and polarization energies of a series of molecular semiconductors in good agreement with available experimental values. Importantly, this tuning method can enforce the negative frontier molecular orbital energies (-εHOMO, -εLUMO) that are very close to the corresponding IPs and EAs. The success of this tuning method can be further attributed to the fact that the tuned RS functional can provide a good balance for the description of electronic localization and delocalization effects according to various molecular systems or the same molecule in different phases (i.e. gas and solid). In comparison, other conventional functionals cannot give reliable predictionsbecause the functionals themselves include too low (i.e. PBE) or too high (i.e. M06HF and non-tuned RS functionals) HF%. Therefore, we believe that this PCM-tuned approach represents an easily applicable and computationally efficient theoretical tool to study the energy levels of more complex organic electronic materials.
Organic semiconductor; Density functional theory; Optimally-tuned; Range-separated (RS) functional; Energy level
December 27, 2016; Revised: March 6, 2017; Published online: April 7, 2017.
O641
��Bredas, J. L. Mater. Horiz. 2014, 1, 17.
10.1039/c3mh00098b
doi: 10.3866/PKU.WHXB201704071
*Corresponding author. Email: htsun@phy.ecnu.edu.cn.
The project was supported by the National Natural Science Foundation of China (21603074, 11474096) and Shanghai-International Scientific Cooperation Fund, China (16520721200).
国家自然科学基金(21603074, 11474096)和上海市国际科技合作(16520721200)资助项目
© Editorial office of Acta Physico-Chimica Sinica

