基于改进粒子群算法的动态无功优化研究
徐朝阳,王孝友,徐德贵,徐中辉
(1.池州供电公司,安徽 池州 247100;2.榆树大岭第二中学,吉林 榆树 130414)
基于改进粒子群算法的动态无功优化研究
徐朝阳1,王孝友1,徐德贵2,徐中辉2
(1.池州供电公司,安徽 池州 247100;2.榆树大岭第二中学,吉林 榆树 130414)
根据电力系统中负荷不断变化的情况,提出了动态无功优化的数学模型,并依据负荷曲线的变化特点进行智能分段。对粒子群算法进行改进,使其具有更好的收敛性和精确度,有效的避免了陷入局部最优解的情况。IEEE6节点系统算例分析表明,改进后的粒子群算法相比改进前的粒子群算法有明显的改善,能够减小系统网损。
动态无功优化;粒子群算法;负荷曲线分段
随着人类进入21世纪,社会得到了高速的发展,而电网规模也相应的越来越大,社会各界对电力的需要日益增加,其中电力系统能否安全与稳定运行则成为一个不可忽视的问题。我国近年来电网发展迅速,网络损耗问题已经是主要矛盾之一,因此,节能损耗是在保证电能质量的同时,尽量降低的指标,也是工作之中的重点。种种条件下,电力系统无功调节,就受到了广泛的关注,如何充分利用无功调节手段,在保证用户正常用电的前提下,能减少系统的损耗,保证系统安全、稳定的运行,就成为了广大学者的研究内容。
现今,国家经济发展,国民日常生活都离不开电,所以保证电能质量非常重要。衡量电能质量最重要的指标之一是电压质量,系统的运行电压太高,极容易超过设备的耐受极限,影响系统的安全稳定运行;而电压过低则会增加耗损,影响系统的经济性,引起电压崩溃,造成重大电力事故[1]。国内外发生过很多次由于电压不稳而造成的重大事故,比如1983年瑞典大停电,导致国民经济损失巨大,1970年美国纽约大停电,1987年日本东京大停电都是由于高峰负荷时,无功不足,造成电压崩溃,引起了巨大的电力事故[2]。若系统中无功电源和无功装置不足,将会导致电网中流动大量无功功率,不仅要消耗有功功率,还会增大线路损耗,增大线路压降,供电的安全性和经济性随之降低[3]。通过有效的无功优化调节,可以使电网安全稳定经济的运行。
传统的无功优化又叫静态无功优化,静态无功优化不考虑控制设备是否允许连续调整,因此,静态无功优化实际上还不能满足运行需要,其结果无法应用于实际无功调度,只能作为网络运行方式的参考[4]。随着无功优化问题的发展,动态无功优化概念被提出。动态无功优化是指在网络参数及未来一天各负荷母线的有功、无功变化曲线及有功电源出力给定的情况下,通过调节发电机的无功出力、电容器组的出力及有载调压变压器的分接头,在满足各种约束条件下使整个电网的电能损耗最小[5]。完整的动态无功优化应该是考虑到各设备的动作次数限制的同时,在满足约束条件的情况下,尽量使电网的损耗最小的优化问题。
我国电力行业迅猛发展,电网规模日益扩大,电网结构越来越复杂,系统的稳定性问题更是不容忽视。输电电压的提高,使输电功率的变化和高压线路上的投切会导致很大的无功功率变化,系统对无功功率和电压的调节能力要求越来越高,另外由于电力市场化的变革,为了充分利用系统资源,现在的电网大多是处在极限状态下运行的,这就导致了电网在遇到紧急情况的时候,灵活解决突发事件的能力大大降低,通过无功优化控制,则可以改善电压质量,降低系统网损,提高系统稳定性。
电力系统无功优化,就是通过电力系统无功潮流分布,使系统电压稳定在一个水平,提高系统的稳定性,降低系统网损。由于电网规模日益扩大,用户对电能质量的要求必定会提高,那么研究无功优化问题,有着很大的实际应用价值[6]。
无功优化问题是多变量,多约束的复杂性非线性优化问题,其目标函数与约束条件都是非线性的,控制变量既有离散的,又有连续的,这就大大的增加了无功优化问题的复杂性。
1 动态无功优化问题的数学模型
动态无功优化是已知未来一天的系统负荷曲线与母线负荷分布的前提下进行计算的。通常配电网的日系统负荷预报和母线负荷预报会给出未来24 h内的系统有功负荷数据和各母线有功负荷在系统负荷中的比例,并根据负荷的功率因数统计值算出母线无功负荷[7]。
电网的实际负荷是连续变化的,但连续的负荷曲线是不利于求解的。通常的处理方法是将负荷曲线分段,并认为每段内负荷保持不变,而分段越多越接近实际最优解,求解越复杂[8]。
在实际运行中,为了延长设备的使用时间,在一定时限内对控制设备的允许操作次数有一定的限制,每个控制变量都不允许超过某个上限的约束。正是这个约束大大的增加了动态无功优化问题的难度。如果不考虑动作次数的限制,那么电网在各时段的最优运行方案只与当前状态有关,与其它时段是相互独立的,完全可以按负荷的分段转化为静态优化,那么动态优化在时间上的复杂性就不存在了。而动作次数限制使得各时段的状态不再独立,也使动态无功优化问题变成了一个必须从整体时间上考虑的全局性优化问题[9]。
本文以全天系统网损之和最小为目标函数,则其动态优化模型可定义为

满足约束条件


uimin≤ui≤uimax,
QGimin≤QGi≤QGimax,
Qcimin≤Qci≤Qcimax,
Timin≤Ti≤Timax,
其中:nl为系统总支路数;Gij连接支路i-j的电导;δi、δj分别为节点i、j的相角;Pi、Qi分别为节点i注入的有功、无功功率;ui、uj分别为节点i、j的电压;uimax和uimin分别为节点i的电压幅值上下限;QGi为节点i发电机无功出力;QGimin和QGimax分别是节点i发电机无功出力上下限;QCi为第i个无功补偿装置的无功补偿容量;QCimin和QCimax为第i个无功补偿装置的无功补偿容量上下限;Ti为第i台有载调压变压器变比;Timax和Timin为第i台有载调压变压器变比可调节的上下限。
2 负荷曲线智能分段
一般来说,动态无功优化问题是完全可以转化成为若干单个时段内的静态无功优化问题来求解,这样就会使问题大大简化。但是,如果时段分的不够多,则会使结果和实际准确值相差太多,影响结果的准确性,而时段分的过多,则会使计算过程变得非常的复杂,计算时间也会相应的增加。所以,合适的分段既能使计算过程相对简单化,又能使结果的准确性有充足的保证[10]。
负荷曲线的分段的关键是如何确定各段的起始和终止时间点。利用智能算法对负荷曲线进行分段,解决设备动作次数约束问题,进而把动态无功优化问题转化为几个时段上的静态无功优化问题[11]。若将整个曲线划分为N段,则需要N-1个划分点。划分的目标就是要使得各个时段内负荷的平均值较为接近,用函数表示则为



上述两个函数都是要求每个负荷段内的负荷值越集中越好,而不同的负荷段的负荷平均值差距越大越好,这会导致分段数增加。但是有了确定的分段数约束,就可以保证合理化。可以综合考虑负荷水平和负荷曲线的变化趋势以及被偿装置的动作次数限制,先确定分数,然后再对负荷曲线进行划分[12]。
由以上的函数可以看出,负荷曲线的自动分段问题本质上也是一个离散的优化问题,可以采用遗传算法来进行求解,其待求变量为N-1个划分点,而且对于初值的选取也十分方便,因为大量的以往的负荷数据和调度人员的经验可以作为分段点的初值,智能分段后,其优化目标函数为

如果分段过多,虽然可以使控制方案更加接近真实最优解,但是同时优化方案的求解复杂程度也会大大提高,而且设备的调节次数也会增加,无法达到真正的简化控制方案的目的。如果分段过少,虽然控制方案变的非常简单,但是无法达到有效降低网损的目的,无功优化的意义就不大,所以过多或过少分段都不合适,应该同时综合考虑计算效率和调节次数两方面的因素。考虑到电容器的最大动作次数一般是3次-5次,一般的负荷曲线只有一个荷峰和一个荷谷,因此确定3段-5段是比较合理的。
设已确定分点数t1、t2、…,tN-1,则可以确定各时段的起始和终止时间,可以在各个负荷段中选取典型负荷点,包括负荷曲线的拐点、驻点和负荷大小的中间点,记录相应的有功、无功功率大小和对应时间,以及该段内的最大、最小负荷。对于一个时段选取平均负荷参加优化计算,得到优化控制方案,根据控制方案得到的设备投切值,再对该时段的最大、最小负荷进行潮流计算,检验是否会出现某些节点电压超限,若出现电压超限则说明分段不合理,需要对负荷曲线进行再划分。
3 粒子群算法
粒子群算法最初是由Eberhart和Kennedy于1995年受人工生命研究结果启发,在模拟鸟群觅食过程中的迁徙和群集行为时提出的一种基于群体智能的深化计算技术[13]。粒子群算法也是进化算法的一种,它是从随机解出发,通过迭代寻找最优解,也是通过适应度来评价解的品质。它具有很好的鲁棒性和全局搜索能力,既适合科学研究,又合适工程应用。
粒子群算法初始化为一群随机粒子,然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个极值来更新自己。第一个就是粒子本身所找到的最优解,这个叫做个体极值,另外一个是整个种群目前所找到的最优解,叫做全局极值[14]。
假设在n维搜索空间中,m个粒子组成一个粒子群,其中Xi=[Xi1,Xi2…Xin]表示第i个粒子的位置,Vi=[Vi1,Vi2,…Vin]表示第i个粒子的速度,粒子个体经历的最好位置为Pi=[Pi1,Pi2…Pin],整个种群所经历的最好位置表示为Pg=[Pg1,Pg2…Pgn],则粒子的速度和位置根据如下公式来变化:


式中:i=1,2,…,m,m为粒子群中粒子的个数;d=1,2,…,n,n为解向量维数;c1,c2为加速常数,通常c1=c2=2;ω为惯性权重,改变其大小可以改变搜索能力的强弱;r1,r2为两个独立的、介于[0,1]之间的随机数。
4 针对粒子群算法所做的改进
(1)惯性权重的改进
通常惯性权重由下式确定:

式中:ωmax和ωmin分别为ω的最大值和最小值;iter和itermax分别为当代迭代次数和最大迭代次数。为了提高粒子的搜索效率,将ω设置为从0.9-0.3的线性下降,使得粒子群算法在开始时搜索较大的区域,较快的确定出最优解的大致位置,随着ω的逐渐减小,粒子的速度减慢,开始局部精确搜索。这样既加快了速度,又提高了粒子群算法的性能。
上式表明惯性权重在随着迭代过程线性下降。在开始的时候为最大值,后逐步减小,直至达到下限。推荐ωmax=0.9,ωmin=0.3 。
(2)加速常数的改进
若c1=0,则粒子没有认知能力,比标准算法更容易陷入局部最优点。
若c2=0,则粒子之间没有社会信息共享,得到最优解的概率就会小的多。
c1=c1s+iter(c1e-c1s)/itermax,
c2=c2e+iter(c2e-c2s)/itermax,
其中:iter和itermax分别是当代迭代次数和最大迭代次数;c1e和c2e分别为c1和c2的终值;c1s和c2s分别为c1和c2的初始值。模拟实验表明,当c1递减至0.15,c2递增至2.15时,算法获得的适应值最优。
5 实验算例及其分析
本文采用IEEE-6节点系统给定的负荷为基准值,采用典型日负荷预测曲线[15](见图1)作为分段标准,假设变压器分接头的调节和和电容器在1 d内的最大调节次数不超过6次,并假设系统中各节点负荷变化一致,都以该负荷曲线的变化趋势为准,形成IEEE-6节点系统的动态无功优化问题。

图1 某典型日负荷预测曲线
利用本文方法对此负荷曲线进行分段,根据负荷曲线的情况,并基于每段内负荷平均值离散较小,段与段之间负荷平均值离散相对较大的原则,可以将此负荷曲线分成5段,分别为0:00-7:00,7:00-11:00,11:00-18:00,18:00-22:00,22:00-14:00。
经过对负荷曲线的分段,我们可以得出新的系统负荷曲线,如图2所示。
对所分出的5个大时段综合利用粒子群算法进行优化,各个时段的负荷取整个大时段的负荷平均值进行优化,可以得出,系统在投入优化前的有功损耗为1.762 4 p.u,而采用了优化控制后,一天的有功损耗为1.382 7 p.u,有效的减少了系统的有功损耗。
IEEE-6节点系统包含2台发电机,2台变压器,2个无功补偿负荷节点,控制变量为发电机端电压VG1,VG2,变压器分接头档位T1,T2和电容器投切容量QC1,QC2,具体参数如表1所示,参数的基准容量为100 MV·A。其中,发电机G1、G2端电压取值范围为1.0~1.1和1.1~1.5,变压器档位调节范围为0.9~1.1,电容器分10组投切,节点4和节点6处电容器容量为0.5 MV·A和0.55 MV·A,采用改进粒子群算法进行优化,种群规模为20,最大进化次数为200次。系统初始状态下,网络损耗为11.61 MW,节点3电压最低,标幺值为0.860。
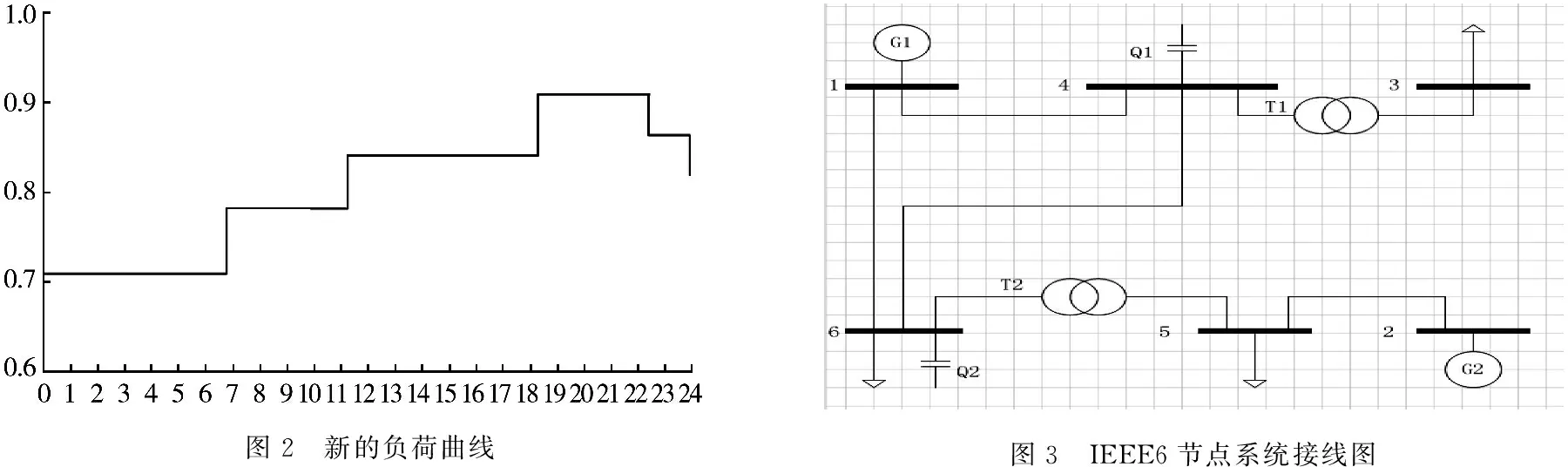
图2 新的负荷曲线图3 IEEE6节点系统接线图

表1

表2 系统优化控制变量

表3 系统优化计算结果
注:系统网络总损耗为8.72MW,上表中数值为标幺值。

表4
由表2、表3、表4可以看出,使用本文提出的改进粒子群优化算法进行优化时,在满足各种约束条件后,实现了系统的有功损耗最小。
同时,由图4可知,改进后的粒子群算法具有很好的收敛性。

图4 计算IEEE6节点系统收敛过程曲线图
6 结 论
本文对负荷曲线进行智能分段,有效的降低了一天内的系统网损。同时针对传统粒子群算法进行改进,既保留了搜索能力强,收敛速度快等优点,又能在一定程度上避免陷入局部最优解。通过对IEEE-6节点系统的计算表明,该方法有稳定的收敛性和较高的计算精度,与传统粒子群优化算法相比,能有效的降低系统损耗。
[1] 蔡昌春,晓群,王宽,等.动态无功优化的简化方法及实现[J].电力系统自动化,2008,32(5):43-46.
[2] 缪楠林,刘明波,赵维兴.电力系统动态无功优化并行算法及其实现[J].电工技术学报,2009,24(2):150-157.
[3] 刘明波,朱春明,钱康龄,等.计及控制设备动作次数约束的动态无功优化算法,中国电机工程学报,2004,24(3):34-40.
[4] 张勇军,任震.电力系统动态无功优化的调节代价[J].电力系统自动化,2005,29(2):34-60.
[5] 摄伟,刘键,周艳.考虑时段优化的地区电网无功优化控制[J].电力系统自动化,2009,33(4):31-35.
[6] 颜伟,田甜,张海兵,等.考虑相邻时段次数约束的动态无功优化启发式策略[J].电力系统自动化,2008,32(10):71-75.
[7] 黄伟,刘明波,赖永生.求解动态无功优化问题的解耦算法[J].电力系统及其自动化,2010,22(5):31-35.
[8] 张勇军,俞悦,任震,等.实时环境下动态无功优化建模研究[J].电网技术,2004,28(12):12-15.
[9] 任晓娟,邓佑满,赵长城,等.高中压配电网动态无功优化算法的研究[J].中国电机工程学报,2003,23(1):31-36.
[10] 吴文传,张伯明.能量损耗最小的无功补偿动态优化算法研究[J].中国电机工程学报,2004,24(4):68-73.
[11] 刘蔚,韩祯祥.配电网无功补偿的动态优化算法[J].中国电机工程学报,2006,26(5):79-85.
[12] 庞松岭,穆钢,王修权,等.基于负荷规律性分析的支持向量机短期负荷预测方法[J].东北电力大学学报,2006,26(4):1-6.
[13] 王秀云,杨龑亮,王彬,等.模拟渔夫捕鱼寻优算法的无功优化[J].东北电力大学学报,2011,31(2):62-66.
[14] 许秀丽,王震宇,王洪军,等.基于细菌群体趋药性算法的电力系统无功优化[J].东北电力大学学报,2009,29(4):1-6.
[15] 蔡泽祥,王明秋,雷亚洲.电力系统长期动态仿真中的统一负荷模型[J].东北电力学院学报,1998,18(1):9-13.
Research on Dynamic Reactive Power Optimization Based on Improved PSO
Xu Zhaoyang1,Wang Xiaoyou1,Xu Degui2,Xuzhonghui2
(1.Chizhou Power Supply Company,Chizhou Anhui 247100;2.The Yushu Daling Middle School,Yushu Jilin 130414)
According to the change of load in power system,the mathematical model of dynamic reactive power optimization is put forward,according to the characteristics of load curve get the intelligent segmentation.Improved particle swarm optimization algorithm,which has better convergence and accuracy,and effectively avoid the local optimal solution.The analysis of IEEE6-node system shows that the improved PSO has obvious improvement compared with the PSO,can reduce the system network loss.
Dynamic reactive power optimization;PSO;Intelligent load curve segments
2016-12-16
徐朝阳(1988-),男,硕士,工程师,主要研究方向:电压稳定与FACTS元件.
1005-2992(2017)03-0033-06
TM714.3
A
电子邮箱: sss317@126.com(徐朝阳);wxy0566@qq.com(王孝友);1093110704@qq.com(徐德贵);xuzhonghui111@126.com(徐中辉)

