小议如何从图形特征中进行知识迁移

井泉

[摘 要]在思考活动中获取的经历性体验称为思维经验，其要义是思维方式的经验。课堂上，学生思维活动的开展是在感悟和体验中进行的。教学“长方形和正方形的周长”时，教师可从图形的特征入手，通过反复比较、层层剖析，使学生学会用特殊的思维方式应对特殊的图形，从而积累数学思维经验。

[关键词]图形特征；知识迁移；小学数学

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2017）17-0038-01

数学教学既要让学生掌握知识技能，又要让学生发展思维，积累经验。而经验的积累主要包括“实践经验”和“思维经验”。相对于“实践经验”，“思维经验”更为抽象、隐秘。因此，教师要让学生在实践中经历思维的全过程，挖掘思维本源。笔者现以“长方形和正方形的周长”一课为例谈谈如何引导学生进行知识迁移，积累思维经验。

一、在描绘中挖掘本源，在比较中寻求突破

【环节1】

出示三个图形：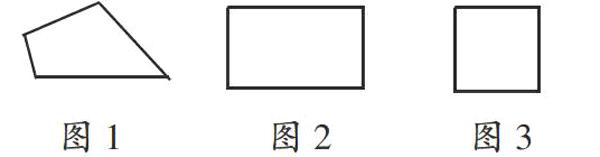

师：你能勾画出这三个图形的周长吗？

（学生用手指勾画出图形所有的边）

在此環节中，学生的思维起点是“周长的意义”。学生只有彻底理解了“封闭图形一周的长度就是它的周长”后，才能准确勾画出周长。让学生勾画图形周长，就是为了充分挖掘学生思维的本源，摸清学生思维的真实过程。

【环节 2】

师：你能试着求出这几个图形的周长吗？请你量一量、算一算。

生1：我测量了图1四条边的长度，把它们的长度相加就得出周长了。

生2：我测量了图2的两条邻边，再把两条邻边的长度分别乘以2即可求出周长。

生3：我测量了图3的一条边长，用这个长度乘以4就可得出周长。

不同的方法代表不同的思维层次，但解决问题的基本原理是一样的，都是求出封闭图形所有线段的总长。为什么会出现不同的测算方法，除了学生思维的角度和深度不同外，还有别的原因吗？学生通过观察不难发现：图2是长方形，对边相等；图3是正方形，每条边都相等；图1是个不规则四边形，各边的长度均不相等。原来，不同的图形有不同的求周长的方法，相同的图形也有不同的求周长的方法，奥秘在于把握图形的特征。通过反复比较、层层剖析，学生的认知水平和思维水平都得到了突破。

二、在反思中明确方向，在迁移中建立模型

【环节3】

师：我们用不同的方法分别把三个图形的周长求都出来了，其中有什么规律吗？

生1：都可以通过累加四条边的长度来求周长。

生2：还可以根据图形的特征进行简便计算。

师（小结）：周长的算法与图形的特征紧密相关。

学生只有在不断的思辨中才能进一步发展思维能力，才能积累思维经验。。教师在教学中可引领学生通过类比领悟逻辑原理，从而积淀经验发展能力。

【环节4】

拓展环节：出示题目“寻找差不多”（如下图）。

师：要量几条边才能求出上面图形的周长呢？说说你的理由。（学生积极互动交流）

这个看似简单的环节，却能让学生的思维真正参与到数学活动当中。当学生思考“要量几条边才能求出图形的周长”时，他们就是在总结图形的最基本特征，对特殊的图形进行分类，并不自觉地以长方形、正方形为分类模板。学生的数学思维一直处于积极探索中，通过类比，学生深化了对数学的认知，提升了数学思维水平。

三、在拓展中提升品质，在发散中拓展空间

【环节5】

师：要求彩带的长度，实际上就是求哪几条边？

生：两条2分米、两条1分米，再加上蝴蝶结所用彩带的长度。

彩带所围成的图形处于三维空间中，学生需要借助想象才能完成。只有让学生的思维参与这样的拓展活动，学生的学习经验才会有长足的增长。必要的提高训练既可发展学生的思维能力，还能提高学生运用已有知识解决问题的能力。因此，教师在进行思维拓展时，要选有一定挑战难度的题目，让学生在解决问题的过程中提升思维品质。

（责编 罗 艳）