基于层次分析法的教师教学质量模糊综合评价*

全建勇, 全晏春, 马联华

(1.重庆师范大学 数学科学学院，重庆 401331；2.重庆市云阳江口中学校，重庆 404506；3.重庆安全技术职业学院，重庆 404020)

基于层次分析法的教师教学质量模糊综合评价*

全建勇1, 全晏春2, 马联华3

(1.重庆师范大学 数学科学学院，重庆 401331；2.重庆市云阳江口中学校，重庆 404506；3.重庆安全技术职业学院，重庆 404020)

针对影响教师教学质量的因素具有模糊性的特点，提出对教师教学质量进行模糊综合评价；采用层次分析法确定指标权重，建立教师教学质量评价的模糊综合评价模型；根据评价结果进行分析，提出了促进教师教学质量发展的具体对策。

主客观结合；一致性条件；模糊；教学质量

教师教学质量评价是我国每个学校都比较重视的活动，其评价结果是校领导对教师评估的重要依据。评价教师教学质量是一项繁琐且复杂的工作，但也是一项必须完成的工作。目前已经有许多教师教学质量评价方面的方法，比如层次分析法、模糊评价法；有综合两种或两种以上方法进行研究的，比如层次分析和灰色关联相结合的方法、灰色关联和模糊评价相结合的方法以及其他方法的综合。在这些科研成果的基础上，本文研究了高阳中学的教师教学质量，以层次分析法为基础，对5位老师的教学质量进行模糊综合评价。

1 用层次分析法求解指标权重

1.1 建立指标体系

通过查阅高阳中学教学相关资料，并根据任课教师的实际情况，建立教师教学质量评价指标体系,其中目标层记为A;准则层包含4个1级指标，分别记为B1,B2,B3,B4;方案层包含11个2级指标分别记为C1,C2,C3,…,C11，如图1所示。

1.2 确定指标权重

1.2.1 推导结论1

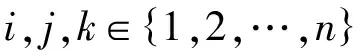
结论1 若判断矩阵满足一致性条件，则判断矩阵中的每一个元素qij的值表示的指标之间的重要性与最初两两指标比较的结果相同。由文献[1]知，判断矩阵若具有一致性，其最大特征值为判断矩阵的维数n，则有CI=0,从而CR=0<0.10,此矩阵为满意一致性矩阵。满足一致性条件的判断矩阵一定具有满意一致性，这样的矩阵无需再作一致性检验。

图1 教师教学质量评价指标Fig.1 Teaching quality evaluation index

1.2.2 推导结论2

以和法为基础对满足了一致性条件的判断矩阵Q=(qij)n×n进行相应的逻辑推理得到第2个结论。

任取判断矩阵Q中的一列，得到列向量Qj={q1j,q2j,…,qij,…,qnj}′，i,j=1,2,…,n。由一致性条件qij=qik×qkj,当k=1时，列向量Qj变成Qj=(q11×q1j,q21×q1j,…,qi1×q1j,…,qn1×q1j)′=q1j×(q11,

q21,…,qi1,…,qn1)′，i,j=1,2,…,n，显然与第1列的列向量成比例。

推广到一般的情况k=1,2,…,n，均有Qj=qkj×(q1k,q2k,…,qik,…,qnk)′，i,j=1,2,…,n，显然与第k列的列向量成比例。

结论2 若判断矩阵满足一致性条件qij=qik×qkj,则判断矩阵各列之间成比例，且对这样的判断矩阵用和法来计算权重。第1步：将判断矩阵Q各列作归一化处理，而归一化处理之后所得的矩阵每一列都相同，当再完成和法的第2步和第3步计算得到的结果与第1步所得矩阵的各列完全相同，则该判断矩阵任意一列元素归一化后所得的列向量即为所求指标的权重系数。

1.2.3 运用层次分析法求权重系数

以专家赋值的方法来确定判断矩阵里面的所有元素。虽然这样得到的判断矩阵很好地融合了资历颇深的专家的经验与知识，但这样的方法太过于主观，精确度不高，很难保证逻辑上的一致性，所以需要进行一致性检验。针对这类问题，可以假设指标的相对重要性在各个指标之间成比例地进行传递，从而判断矩阵的确定方法可简化为以下步骤：请专家按1～9标度法给判断矩阵赋第1行元素的值；运用公式qij=qik×qkj,qij=1/qji计算判断矩阵的其他元素的值；将判断矩阵各列进行归一化处理，处理后的矩阵任意一列构成的列向量即为指标权重[2]。

针对高阳中学教师教学质量的评估问题，在已经建立了指标体系的基础上，运用上面提出的方法先来求解准则层4个指标的权重。

(1) 请相关专家将第1个指标B1与其他3个指标B2,B3,B4分别作比较，按照1～9标度法给判断矩阵第1行元素赋值,得到如下矩阵：

(2) 由公式qij=qik×qkj,qij=1/qji可得q23=q21×q13=1/q12×q13=3/2。同理可算得q24=3/5,q34=2/5。再根据判断矩阵为正反矩阵的性质可得如下判断矩阵：

(3) 将矩阵Q各列进行归一化得：

(4) 由步骤(1)—(3)可得准则层4个1级指标的判断矩阵和权重如表1所示，同理可得方案层的4个判断矩阵和权重如表2到表5所示。

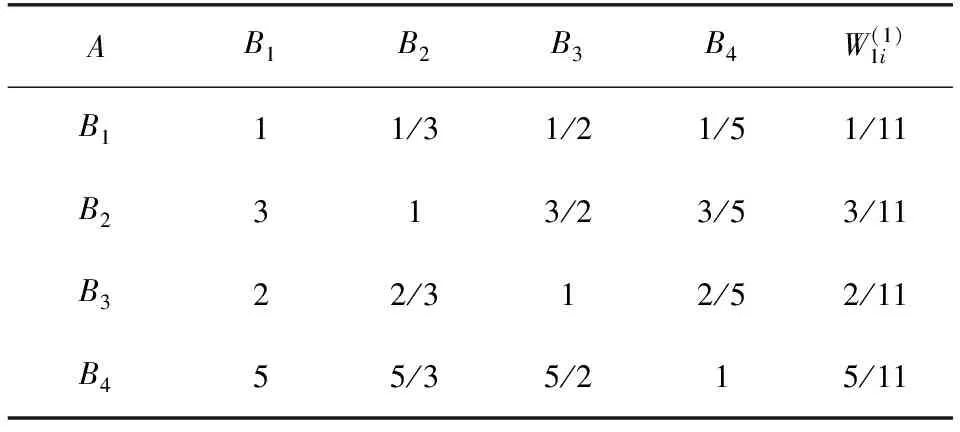
表1 判断矩阵QA-B

表2 判断矩阵QB1-C

表3 判断矩阵QB2-C

表4 判断矩阵QB3-C

表5 判断矩阵QB4-C

(5) 由层次单排序的结果，可以算得11个2级指标的总权重，得到层次总排序如表6所示。

表6 指标总权重

2 模糊综合评价

2.1 收集原始数据

请高阳中学的领导和教学专家给该校的5位任课教师进行打分，并规定每项指标的满分为10分，收集到的评价数据如表7所示。

表7 原始数据

2.2 计算隶属度

因为所选的11个指标均为越大越优的正向指标，用符号∧和∨分别表示取小、取大符，所以第i位教师相对第j个指标的隶属度可表示为

由原始数据和隶属度的计算公式可以算得每位老师各个评价指标的隶属度，结果如表8所示，其中列表示5位教师，行表示11个评价指标。

表8 隶属度

2.3 构造模糊矩阵

由表8写出模糊矩阵：

2.4 进行总评价

先用教师教学质量二级指标的权重向量乘以模糊矩阵，求出每位教师在各个一级评价指标下的模糊评价值，得到4个模糊评价值向量分别记为E1，E2，E3和E4。

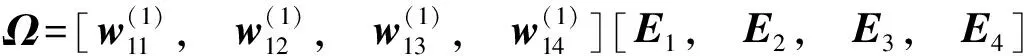
考虑高阳中学的教师数量很大，为了研究结果更符合实际，分别从青年教师、中年教师以及老年教师里面各抽取20名教师作为研究对象，即从高阳中学抽取60位教师，并收集相关数据，由于样本量比较大，可运用MCE软件计算指标权重，用MATLAB软件计算隶属度和总评价结果，从而对60名教师的教学水平作出评价。

3 结 论

通过运用主客观相结合的方法确定判断矩阵，不仅融合了专家们丰富的经验和知识，而且确保了逻辑上的严密性，即满足了一致性条件，不用作一致性检验，对于这样的判断矩阵计算指标权重比较简单。文中结合原始数据运用隶属度公式计算出的模糊评价矩阵具有可靠性，使得后面做的模糊总评价比较符合实际情况。

为了评价结果更加准确，本文将样本量扩大到60，当样本量比较大的时候，应当运用统计软件来计算数量结果，从而得到60名教师的评价结果。根据评比结果，可以有针对性地管理教师，对不同的教师采取不同的措施，从而提升整个学校的教学水平。

[1] 杜栋，庞庆华，吴炎.现代综合评价方法与案例精选[M].北京：清华大学出版社，2008

DU D,PANG Q H,WU Y.Modern Comprehensive Evaluation Method and Case Selection[M].Beijing:Tsinghua University Press,2008

[2] 廖红强，邱勇，杨侠，等.对应用层次分析法确定权重系数的探讨[J].机械工程师，2012(6)：22-25

LIAO H Q,QIU Y,YANG X,et al.The Discussion on Application of Analytic Hierarchy Process to Determine the Weight Coefficient[J].Mechanical Engineer,2012(6):22-25

[3] 陈静.基于层次分析法和灰色关联度分析的高校教师教学质量评价研究[J].贵阳学院学报(自然科学版)，2016,3(1)：22-27

CHEN J.Research on Teaching Quality Evaluation of College Teachers Based on Analytic Hierarchy Process and Grey Relational Analysis[J].Journal of Guiyang University (Natural Science Edition),2016,3(1):22-27

[4] 周罕,曹平.软土地区城市深基坑支护方案优选的模糊层次分析法[J].中南大学学报(自然科学版),2012,43(9):3583-3588

ZHOU H,CAO P.Fuzzy Analytic Hierarchy Process for the Optimization of Deep Foundation Pit Support in Soft Soil Region[J].Journal of Central South University (Natural Science Edition),2012,43(9):3583-3588

[5] 杨建仁，刘卫东.基于灰色关联分析和层次分析法的新型工业化水平综合评价:以中部六省为例[J].数学的实践与认识，2011,41(2)：122-132

YANG J R,LIU W D.A Comprehensive Evaluation of New Industrialization Level Based on Grey Relational Analysis and Analytic Hierarchy Process in Six Provinces of Central China as an Example[J].The Practice and Understanding of Mathematics,2011,41(2):122-132[6] 刘亚臣,常春光,刘宁等.基于层次分析法的城镇化水平模糊综合评价[J].沈阳建筑大学学报(自然科学版)，2008,24(1):132-136

LIU Y C,CHANG C G,LIU N,et al.Fuzzy Comprehensive Evaluation of Urbanization Level Based on Analytic Hierarchy Process[J].Journal of Shenyang Construction University (Natural Science Edition),2008,24(1):132-136

责任编辑：李翠薇

Fuzzy Comprehensive Evaluation of Teachers’ Teaching Quality Based on Analytic Hierarchy Process

QUAN Jian-yong1, QUAN Yan-chun2, MA Lian-hua3

(1. School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, China； 2. Chongqing Yunyang Jiangkou School, Chongqing 404506, China;3. Chongqing Safety Technology Profession Academy, Chongqing 404020, China)

According to the fuzziness of the factors affecting the teaching quality of the teachers, the teachers' teaching quality fuzzy comprehensive evaluation is pointed out by using AHP, fuzzy comprehensive evaluation model of teaching quality evaluation; according to the analysis of the evaluation results, the specific measures to promote the development of teachers’ teaching quality is put foward.

combination of subjective and objective conditions; consistency condition; fuzzy; teaching quality

10.16055/j.issn.1672-058X.2017.0003.008

2016-11-10;

2017-01-19. * 基金项目：重庆市教委项目(KJ130658，KJ1400521).

全建勇(1990-)，女，重庆奉节人，硕士研究生，从事应用统计研究．

O223

A

1672-058X(2017)03-0034-06