AHP和模糊综合评判法在企业合作伙伴选择上的应用

高 露 露

(重庆师范大学 数学科学学院，重庆 401331)

AHP和模糊综合评判法在企业合作伙伴选择上的应用

高 露 露

(重庆师范大学 数学科学学院，重庆 401331)

对于SDN企业在合作伙伴中的选择问题，文章首先由相关专家根据各指标因素的相对重要程度对其赋予相应的权重，然后利用层次分析法由各级判断矩阵求得各层次指标的权重，最后通过赋予恰当的主观权系数将这两种权重进行加权平均从而得到各指标的最终权重；再运用模糊综合评判法确定各个方案的评价指标，然后进行综合排序并得到评判结果；最后结合具体实例验证了该方法的实用性。

模糊综合评判；层次分析法；主观权系数

随着经济的快速发展，SDN企业在其发展的过程中面临巨大的挑战，如市场利益复杂化、竞争力加大等。另外，企业竞争力指的是在市场上能够持续地、有效地向市场提供服务，同时企业本身可以获得利益并且能够为自身的发展提供更多的支持，它对企业的发展有着举足轻重的作用。因此，SDN企业要想获得更好的发展，除了提高自身的竞争力以外，还可以寻求良好的企业合作伙伴共同谋求发展。而在企业合作伙伴选择时，候选企业的价值观、管理水平、发展水平、企业相容性等都是至关重要的，通过一定的决策方法选择最优的合作伙伴能够快速有效地促进企业更好地发展。

1 模型建立

结合层次分析法和模糊综合评判法对SDN企业合作伙伴的选择模型进行研究。根据专家填表最终得到判断矩阵，然后利用层次分析法求得各个评价指标的权重值，再利用模糊综合评判法计算出3个候选合作企业的综合评判结果，最后根据最大隶属度原则选出最佳的合作企业。

1.1 层次分析法的基本原理及步骤

层次分析法(Analytic Hierarchy Process，AHP)是运筹学家T.L.Satty等提出的一种多准则决策方法[1]，方法是将定量分析与定性分析相结合，解决复杂决策问题的一种决策方法。层次分析法的基本步骤如下：

(1) 分析影响所研究的复杂决策问题的因素以及各因素之间的内在联系，然后构建一个包含目标层、准则层和方案层的层次结构分析图[2]。

(2) 对于准则层和方案层，根据在某一准则下，下层各指标间的相对重要性，构造出判断矩阵。一般地，判断矩阵由熟悉该问题的专家给出。

(3) 计算各个指标的相对权重，并对各个判断矩阵进行一致性检验[3]。

1.2 模糊综合评判法的基本原理和步骤

1965年，美国的控制论专家扎德发表了《模糊集合》的论文，第一次提出了模糊的概念，宣告了模糊数学的诞生。模糊综合评判法是运用模糊关系合成的原理，将一些边界不清、不易定量的因素定量化，再根据最大隶属度原则进行综合评判的一种方法，其基本原理如下[4]：

首先确定被评判对象的因素集和评价集；再分别确定各个因素的权重以及他们的隶属度向量，获得模糊评判矩阵；最后把模糊评判矩阵与因素的权向量进行模糊关系和成并进行归一化，得到模糊评价的综合结果。

运用模糊综合评判法，大体可以分为以下4个步骤：

(1) 确定被评价对象的因素集X={x1,x2,…,xm}(其中m为评价因素的个数)和评价集Y={y1,y2,…,yn}(其中n为评语个数，一般划分为3～5个等级)[5]；

(2) 根据m个评价因素的n个评价等级构造出模糊评判矩阵(要对单因素的评判集进行归一化处理，即∑rij=1)；

(3) 对各个因素的权重以及模糊评判矩阵进行模糊合成(一般是通过某种模糊算子得到，常用的两种模糊算子是扎德算计和普通矩阵乘法)，然后对结果进行归一化处理；

(4) 最终根据最大隶属度原则对模糊综合评判结果进行择优选择[6]。

2 在SDN企业合作伙伴选择上的应用

本小节结合某大型SDN企业合作伙伴选择问题[7]，举例说明模糊评判法在企业合作伙伴选择上的应用(该算例采用了文献[7]中的SDN候选合作伙伴选择的问题)，该算例的模糊数学评判模型见表1。

表1 企业合作伙伴选择的二级模型

由聘请的各相关领域的专业人员组成决策专家小组，采用10分制的评分标准，对企业的各个相关指标打分，得到相应的初始评定值(数据直接参考文献[7])。然后采用算术平均值的方法计算得到各指标的相关权重。结果见表2。

表2 用算术平均值法算得的指标权重值

2.1 利用层次分析法计算各个指标层的权重

根据表1的指标因素，由相关专家经过专业综合分析，得出相应的判断矩阵，再经过AHP软件分析(表4—9均采用此软件分析方法得到)，得到相应的指标权重，结果见表3。

表3 第1级指标的评价值

注：λmax=6.196 8,CI=0.039 4,RI=1.24,CR=0.031 7<0.10。

对于产品服务能力的重要性排序，求得数值见表4。

表4 影响产品服务能力的各指标值

注：λmax=3.038 5,CI=0.019 3,RI=0.58,CR=0.033 2<0.10。

对于技术能力的重要性排序，求得数值见表5。

表5 影响技术能力的各指标值

注：λmax=401 866,CI=0.062 2,RI=0.9,CR=0.069 1<0.10。

对合作伙伴企业资质相关指标的重要性排序，求得数值见表6。

表6 影响合作伙伴企业资质的各指标值

注：λmax=3,CI=0,RI=0.58,CR=0<0.10。

对于相容性指标相关影响因素的重要性排序，求得数值见表7。

表7 影响相容性指标的各因素的指标值

注：λmax=2,CI=0,RI=1E-6,CR=0<0.10。

对于可靠性指标相关影响因素的重要性排序，求得数值见表8。

表8 影响可靠性指标的各因素指标值

注：λmax=3.038 5,CI=0.019 3,RI=0.58,CR=0.033 2<0.10。

对于环保低碳指标相关性影响因素的重要性排序，求得数值见表9。

表9 影响环保低碳指标的各因素指标值

Table 9 Factors influencing low carbon index

合作伙伴低碳环保A6A61A62A63合作伙伴的低碳环保形象A61153合作伙伴的低碳环保投资A621/511/3合作伙伴低碳环保的技术水平A631/331权 重0．6370．1050．258

注：λmax=3.038 5,CI=0.019 3,RI=0.58,CR=0.033 2<0.10。

结合专家对各指标赋予的权值以及运用层次分析法求得的权重，运用加权平均法(式(1))求得各个指标的最终权重值，其结果见表10。

(1)

其中θ为主观权系数，α1为专家赋予的权重，α2为层次分析法求得的权重。由于专家对该问题的见解相对具有权威性，所以这里令主观权系数θ=0.6。

表10 各个指标的最终权重值

2.2 利用模糊综合评判法求得最终的综合评判结果

因素集A分为两层：

第1层为A={A1,A2,A3,A4,A5,A6}。

第2层为A1={A11,A12,A13}；A2={A21,A22,A23,A24}；A3={A31,A32,A33}；A4={A41,A42}；A5={A51,A52,A53}；A6={A61,A62,A63}。

该企业有3个候选合作企业，评价集V={甲，乙，丙}，代表3个不同的候选合作企业。

现在由精通企业管理的专家成立决策专家小组，根据评价体系，分别对各候选合作企业的各项指标进行综合打分，评分采用十分制，数据(参考文献[7]的数据)经过处理(选取各个候选企业某一个评价指标对合作价值的隶属度作为最终的评价指标数据)后得到各评价因素的模糊综合评判表，见表11。

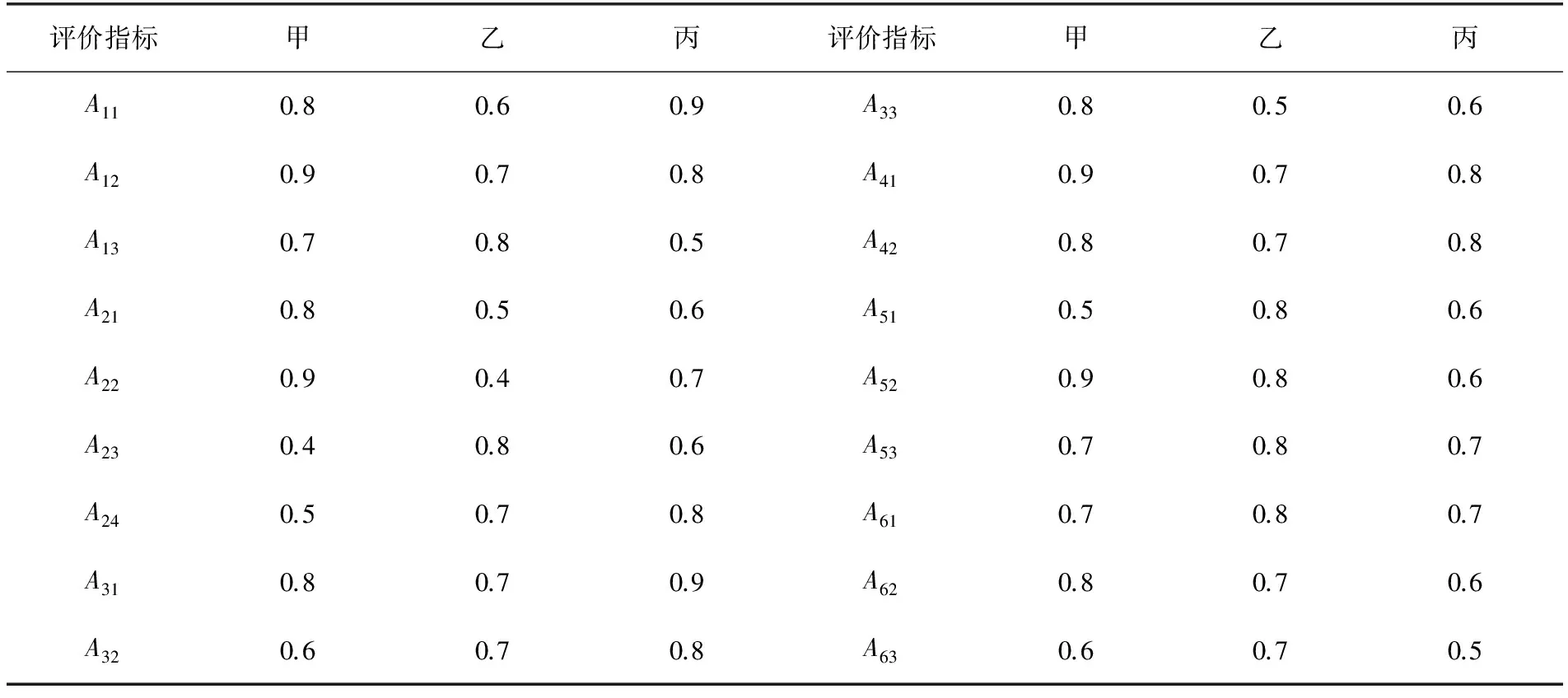
表11 3个候选合作企业的模糊综合评判值

2.2.1 分层次综合评判

A1={A,A12,A13}，权重C1=(0.461,0.256,0.283)，由表11对A11,A12,A13的模糊评判构成单因素评判矩阵：

用模型(这里采用的模糊算子就是普通矩阵乘法)计算得到：

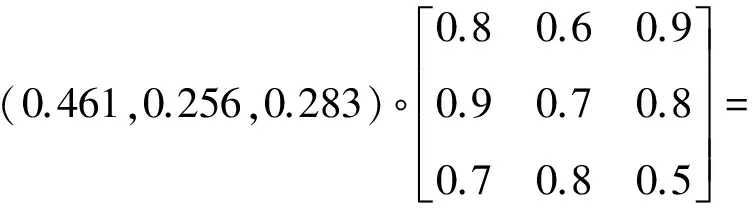
(0.797，0.682，0.761)

类似地

(0.645，0.601，0.693)

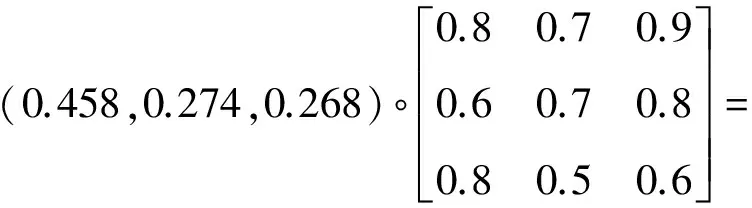
(0.745，0.646，0.792)

(0.851，0.7，0.8)

(0.75，0.8，0.631)

(0.697，0.747，0.619)

2.2.2 高层次综合评判

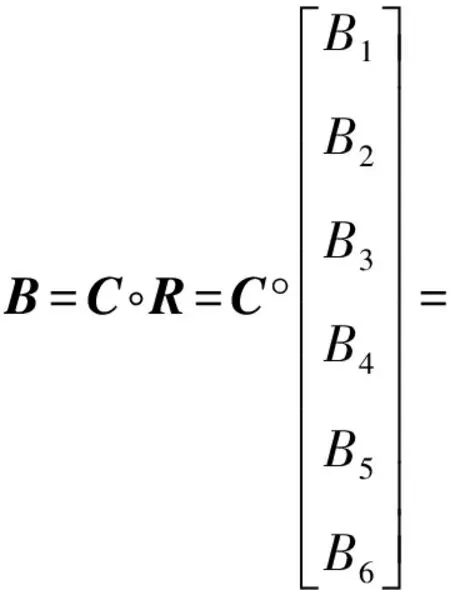
将上述评判指标归一化得高层次综合评判=(0.344，0.321，0.342)，即3个企业的综合排序为甲>丙>乙。所以根据最大隶属度原则，选择企业甲作为该SDN公司最终的合作伙伴。

3 结 论

本例应用AHP和模糊综合评判法对最优企业合作对象进行选择，此模糊评价模型采用层次式结构，把评判因素分为两层。该模型首先由相关专家根据各指标因素的相对重要程度对其赋予相应的权重，然后利用层次分析法由各级判断矩阵求得各层次指标的权重，最后通过赋予恰当的主观权系数将这两种权重进行加权平均从而得到各指标的最终权重，并进行归一化处理，然后将评判结果按照大小顺序排列，决策者从中选取估计值较大的候选企业作为最终的合作伙伴即可。事实证明此方法可行有效，且其权重的可信度更强，在合作企业选择问题的综合评价中，取得了更加可靠的结果。

[1] 刘丹,王佳渊,彭关中.基于模糊层次分析法的导弹阵地防护效能评估[J].山西建筑,2007,33(1):72-73

LIU D, WANG J Y, PENG G Z.Missile Position Protecting Efficiency Evaluation Based on Fuzzy Analytic Hierarchy Process[J].Construction of Shanxi Province,2007,33 (1):72-73

[2] 杨建仁,刘卫东.基于灰色关联分析和层次分析法的新型工业化水平综合评价:以中部六省为例[J].数学的实践与认识,2011,41(2):122-132

YANG J R, LIU W D.Comprehensive Evaluation of the New Type Industrialization Based on Grey Relational Analysis and Analytic Hierarchy Process:A Case Study of the Six Provinces in Central China[J].The Practice and Understanding of Mathematics,2011,41 (2):122-132

[3] 吴从忻,马明.模糊分析学基础[M].北京:国防工业出版社，1991

WU C X,MA M.Basis of Fuzzy Analysis[M].Beijing:National Defense Industry Press,1991

[4] 杜栋,庞庆华,吴炎.现代综合评价方法与案例精选[M].北京:清华大学出版社,2008

DU D,PANG Q H,WU Y.Modern Comprehensive Evaluation Method and Case Selection[M].Beijing:Tsinghua University Press,2008

[5] 李俊芳.基于AHP-FUZZY多层次评判的城市轨道交通线网规划方案综合评价[J].武汉理工大学学报，2007,31(2)：205-208

LI J F.AHP-FUZZY Multi-Hierarchical Evaluation for Comprehensive Evaluation of Urban Rail Transit Network Planning[J].Journal of Wuhan University of Technology,2007,31(2):205-208

[6] 曹柬,周根贵,张定岳.一种基于AHP和模糊理论的多方案综合评价方法[J].浙江工业大学学报,2003,31(4):355-359

CAO J,ZHOU G G,ZHANG D Y.A Multi-Plan Synthetic Evaluation Method Based Upon Ahp and Fuzzy Theory[J].Journal of Zhejiang University of Technology,2003,31(4):355-359

[7] 李金明,陈荔.基于直觉模糊TOPSIS法的SDN企业合作伙伴选择问题的研究[J].物流科技,2015(9):12-18

LI J M,CHEN L.SDN Business Partners and Choose Based on Intuitionistic Fuzzy Topsis Method[J].Logistics Techn-ology,2015(9):12-18

责任编辑：李翠薇

Application of AHP and Fuzzy Comprehensive Evaluation Method to Enterprise Partner Selection

GAO Lu-lu

(School of Mathematical Science, Chongqing Normal University, Chongqing 401331, China)

As for the selection of SDN enterprise cooperation partner, this paper firstly gives the corresponding weight to each indicator factor by experts, then uses analytic hierarchy process (AHP) to derive indicators' weight at every level by determining matrix, finally uses appropriate subjective weight coefficient to average the two weights to derive the ultimate weight of each index, then uses fuzzy comprehensive evaluation method to determine the evaluation index of each case, uses comprehensive ranking to derive judging results and finally uses examples to verify the practicability of this method.

fuzzy comprehensive evaluation; AHP; subjective weight coefficient

10.16055/j.issn.1672-058X.2017.0003.007

2016-11-16；

2016-12-05. * 基金项目：重庆市教委项目(KJ130658，KJ1400521).

高露露(1992-)，女，河南洛阳人，硕士研究生，从事统计评估研究.

O212

A

1672-058X(2017)03-0028-06