感悟减法算式模型意义 破除一图单题思维定式
张宏伟
[摘 要]“减法应用题教学”这一课主要有两大部分,第一部分。通过层层递进的几个数学活动,让一年级的学生在自编的“无数个”用“4-3=1”解决的不同现实问题中,认识减法模型,初步感悟算式模型的意义,及其概括、简洁和一般化)的特点;第二部分,主要通过由一幅图既可以列出加法算式,也可以列出減法算式的辨析和讨论,打破学生一图单题、一图只对应一种运算的思维定式,让学生意识到数学有更多的可能。
[关键词]模型;思维定式;减法应用题
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2017)17-0011-03
一、暖场
师(在黑板上粘贴红、绿、蓝、黄4个笑脸贴画):我要奖励第一个做好课前准备,并且端正坐好、安静等待上课的曹阳同学。
(学生迅速归位,做好准备,安静候课)
师:我这里有很多贴画,凡是积极思考和发言的同学每次都会得到一个贴画奖励。请看黑板,一共有几个笑脸贴画?
生:4个。
师:曹阳,你是第一个安静候课的“小蜜蜂”,请选一个。(曹阳拿走了一个黄色的笑脸贴画)
二、感悟减法算式的模型意义
1.就事编题
师:谁能把刚才这件事编成一道应用题?
生1:黑板上一共有4个贴画,被曹阳拿走了1个,黑板上还剩下3个。
师:我们昨天学习了应用题的结构,先说两个已知条件,然后根据这两个条件提出一个问题。
生2:黑板上一共有4个贴画,被曹阳拿走了1个,黑板上还剩下几个?
师:谁听出了这两个同学说的哪里不同?
生3:生1把剩下的3个说出来了,生2是问还剩下几个。
生4:生1说的三句话都是已经知道的,不需要再求了;生2最后问的是不知道的,要我们求解。
(板书:①一共有 4个■
②曹阳拿走1个
→ 还剩下几个?)
师:这道题用什么方法解答?为什么?
生5:减法,因为是从“一共”的当中拿走了,求剩下的。
师:怎么列算式?
生6:4-1=3。
师:这里的4、-、1和3分别表示什么?
生7:“4”表示一共有4个笑脸贴画,“-”表示拿走,“1”表示被曹阳拿走的那1个,“3”表示黑板上还剩的那3个。
2.看图编题、解答、解说
生8:小猴子的妈妈买来4个桃子,被小猴子偷吃了一个(教师模仿猴子,作偷吃桃子状),还剩下几个桃子?(教师面对盘子,模仿猴子作挠头思考状,学生大笑)
师:如何解答?
(教师故意用了简洁的术语,很多学生不懂教师的意思)
师(进一步解释):就是用什么方法做,怎么列算式?
生9:用减法,用4-1=3。
师:这里的4、-、1和3分别表示什么?
生10:“4”表示所有的桃子,“-”表示偷吃、去掉,“1”表示被小猴子偷吃掉的那1个,“3”表示还剩的那3个桃子。
师:它们在哪里?
生11:盘子里。
生12:一共有4个汽车,被张老师开走了一个。(教师表演开走汽车状,学生微笑)
师:汽车不用“个”来表示,应用“辆”。一共有4辆汽车,谁来试着再编一次?(学生回答,略)
师:如何解答?
生13:用减法,用4-1=3。
师:我还要再写一遍算式吗?
生14:不用了。
师:为什么?
生15:重复了!
生16:什么意思?黑板上已经有两个算式了,都是一样的,就不用写了。
师:这一个也去掉,只留下一个行吗?
生17:行!
【评析:通过“写”还是“不写”,引发学生聚焦和关注“4-1=3”这个由不同问题得到的同种算式(模型),初步感悟到一个算式足以表达三件不同的事。】
师:这里的4、-、1和3分别表示什么?
(学生回应,略)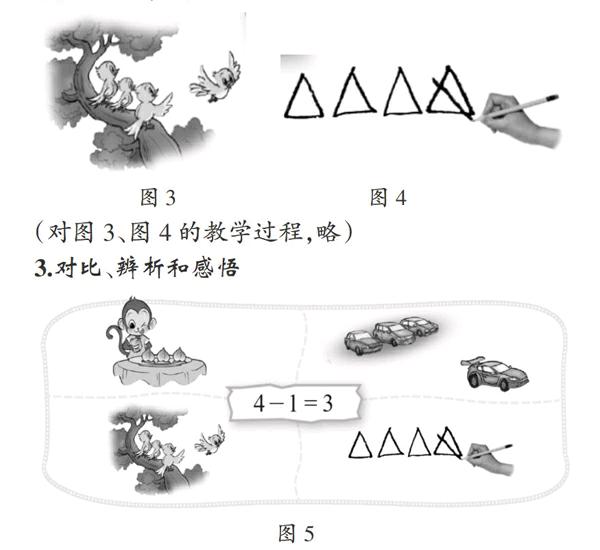
(对图3、图4的教学过程,略)
3.对比、辨析和感悟
师:对于图5你有什么发现?有什么想法尽管说出来。
生18:我发现都是用4-1=3进行计算。
生19:我发现事情不一样,但是算式一样。
生20:我发现虽然结果都是3,但是它表示的图形不一样。
生21:为什么都用4-1=3呢?
师:你们的发现都不错,问题问得更好!这些图不同,图中发生的事情也不同,为什么都能用“4-1”解答?
生22:因为它们原来都是4个,只不过桃子吃了1个,汽车开走了1辆,小鸟飞走1只,三角形划掉了1个。
生23:因为它们一共是4个,都去掉了一个,最后都剩下了3个。
……
【评析:用各种方式帮助学生初步感悟“4-1=3”这个算式模型的概括性、简洁性和一般化特征。】
师:4-1=3可以表示4个笑脸贴画,拿走1个还剩几个;可以表示小鸟飞走了1只还剩几只……除了这五件事,哪些事情还能用4-1=3来表示呢?
师:能说完吗?
生24:说不完。
师:那可以用4-1=3表示的事情有多少件呢?
生25:100件。
生26:不对,无数件,说不完的。
师:觉得4-1=3这个算式怎么样?
生27:很厉害。
生28:它能算很多很多事情。
生29:它能表示无数这样的事情。
师:哪样的事情?
生29:就是从4个拿走1个的事情。
【评析:至此,学生已经对“4-1=3”这一算式模型的意义有了自己的理解,并能用自己的语言进行描述。】
三、中场休息
师(出示一个大挂钟):我们已经上了25分钟的课了,现在的时间是快到几点了?
(教师把每个学生得到的奖励贴画贴在学生的书皮上;学生说快9点了,因为时针快走到9了,长针还不到12;杨凯博同学直接说出现在是9点50分,他课后还教同学:分针指着12代表0,指着1代表5,然后是10、15、20……)
【评析:教师始终坚持全景式长线浸润的学习思想,在开学前的家长会上就曾向家长发出倡议,把方向、认识钟表、感受轻重、比较长短等融入学生的日常生活,让家长在日常生活中注意指导学生辨认,每天睡觉、吃饭、上学都提醒学生注意时间,让学生能够逐步认识几时整,快到几时了,几时多一点了,几时半,快几时半了,几时半多一点。此时,利用中场休息时间进行操作,一举两得。】
四、破除一图单题的思维定式
1.起——看图编加法题
生1:有3只小鸡吃米粒,又有2只小鸡跑过来了,现在一共有几只小鸡吃米粒?
师:怎么解答?
生1:用加法,3+2=5。
师:这里的3、+、2和5分别表示什么?
2.转——看图编减法题
师:我在杭州带的几个学生用这个图编了一道用减法解决的应用题。猜猜他们是怎么编的?
生2:5-3=2。
(教师笑着摇了摇头)
生3:5-2=3。
师:我说编一道用减法解决的应用题,不是看图写一个算式。
生4:一共有5只小鸡在吃米,有2只吃饱了,跑去玩了,还剩下几只小鸡在吃米?
师:你们觉得生4编得怎样?怎样列式计算?
生5:他编得很好,5-2=3。
生6:那2只鸡不是跑了,是来吃米的。
师:这道应用题似乎和图画不大一致。有没有哪个同学能编一个和图一致,又能用减法解决的应用题啊?
(学生都默不作声)
师:我选择最专注的五个同学当小鸡,来演个戏,只要认真看,一定就会编了。
(我选了2个男生和我一起扮演3只公鸡,又选了2个女生扮演2只小母鸡。在黑板前的一个桌子上放一些葡萄干作为米粒。先是5只小鸡都聚在门口。)
师(尖起自己的嘴作公鸡状):你知道我们一共有几只吗?
生(齐):5只。
师(面向桌上的葡萄干):那里有米,快去吃喽!
(5只“鸡”一起跑向桌子,3只“公鸡”跑到桌子周围,围着桌子吃“米”,2只“母鸡”跑到半路)
生7:一共有5只鸡来吃米,3只很快跑到米粒那里吃了起来,还有几只小鸡没有跑到?
师:怎么解答?
生8:用减法5-3=2。
师:如果要用“5-2=3”解答,应该怎么编写?(学生一时无从下手。我们又演了一遍,并提示:这2只“母鸡”好悲催,没跑到,没得吃)
生9:一共5只鸡来吃米,有2只还没跑到,没有吃到米,已经跑到并吃到米的有几只?
3.合——学习小结
师:对于这个图,你们还认为只能编加法题吗?
生10:还能编减法题。
师:谁来把编过的加法和减法应用题都再说一说?
师:不管是编减法题还是加法题,都要注意什么呢?
此时下课铃声响起,我便宣布下课,没想到有一个學生跑到我跟前说:“张老师,编应用题是不是只要编得顺溜就行了?”
我感到非常惊喜!我懂这个学生,他所说的其实是成人世界定义的自洽、自圆其说。我们对一切概念的定义,或者建立阐释一种新主张的基本要求就是自洽。
我激动地拥抱着他,赞叹地说:“是的,只要顺溜就行,只要你能说清楚、说明白,解释得通就可以!”
看,一年级的学生可不容小觑,只要充分地信任和放手,他们的学习便会充满智慧的火花和成长的惊喜。
(责编 金 铃)

