一种混合核函数的支持向量机

刘高辉，杨 星

(西安理工大学 自动化与信息工程学院，陕西 西安 710048)



一种混合核函数的支持向量机

刘高辉，杨 星

(西安理工大学 自动化与信息工程学院，陕西 西安 710048)

为了提高支持向量机分类效果、学习能力和外推能力，分析了两种支持向量机的核函数：K型核函数和logistic核函数，构造出一种新的混合核函数的支持向量机，并且对其性能进行了理论分析。把构造出的混合核函数支持向量机与常用核函数构造的向量机应用到二维数据分类与图片分类中进行实验对比。二维数据点和图片分类的实验结果表明，混合核函数的支持向量机的分类效果、学习能力和外推能力，明显优于常用核函数构造的支持向量机。

K型核函数；logistic型核函数；混合核函数

0 引言

伴随着科学技术的飞速发展以及网络的快速普及，科学发展和生活中出现了许多高维复杂的数据。怎么才能在这些高维复杂的数据中找出其内在特有的规律，以便能够利用这些规律，更好地为人们的生活服务，这对统计学的理论而言成为重中之重。

支持向量机(Support Vector Machines,SVM)是1995年由Vapnik等人提出的一种基于统计学习理论的机器学习方法[1-2]。它通过寻找结构风险最小化来提高机器学习外推能力，从而使得在测试样本量比较小的情况下也能得到较好的统计分类规律[3]。它非常适合解决高维、非线性和小样本的模式识别检测问题，并在一定程度上克服了“过学习”和“维数灾难”等问题。支持向量机分类效果、学习能力、外推能力性能的优劣主要取决于核函数的选择及其参数，尤其是核函数的选择。

因为支持向量机的分类效果、学习能力和外推能力等许多特性是由本身的核函数来决定的，而且每一种核函数都有自己的优点和缺点，所以支持向量机因核函数的不同而表现出的分类效果、学习能力、外推能力有很大的差异。为了同时提高支持向量机分类效果、学习能力和外推能力，本文提出一种混合核函数的支持向量机。

1 传统的核函数

就目前来说常用的核函数有以下几种：

(1)线性核函数

K(xi,xj)=(xi·xj)

(1)

(2)多项式核函数

K(xi,xj)=(γxi·xj+r0)p，γ>0

(2)

(3)径向基核函数(RBF)

(3)

总体来说支持向量机的核函数主要分为:全局核函数和局部核函数。全局性核函数的支持向量机外推能力强、学习能力较弱;而局部性核函数的支持向量机学习能力强、泛化能力较弱。在以上列举的常用核函数中线性核函数和多项式核函数属于全局核函数，径向基核函数属于局部核函数。

2 K型核函数

K型函数的表达式如式(4)所示[4]：

(4)

式(4)中，k>0，且m∈N。

通过观察K型函数与径向基函数的表达式可知：K型函数与径向基函数相比没有费时的指数运算，所以运算速度更快。

K型核函数的表达式如式(5)所示：

(5)

文献[4]已经证明了K型核函数可以作为支持向量机的核函数。

图1为K型核函数与径向基核函数的对比图，其中K取1，m取1，σ取1，测试点为0。由图1可以看出：K型核函数与径向基核函数都是只有在测试点附近的数据才会对核函数的值产生很大影响，而离测试点很远的数据对核函数的值影响很小，所以K型核函数和径向基核函数属于局部核函数。不同的是K型核函数与径向基核函数相比尖端更尖，两端收敛也更缓慢，正是这种特性使得K型核函数比高斯核函数具有更好的外推能力。

图1 K型核函数与径向基核函数对比图

3 logistic型核函数

logistic函数表达式为：

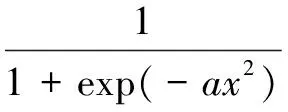
(6)

如果一个函数可以当作支持向量机的核函数那它只要满足Mercer条件即可。

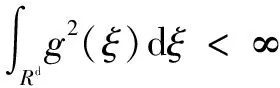
(7)

则K(x,x′)可作为支持向量机的核函数。

如果K(x,x′)=K(x-x′)，则K(x,x′)称为转移不变核函数。转移不变核函数要证明满足Mercer条件，是十分困难的，而下面的引理1很好地解决了这个问题。

引理1转移不变核函数K(x,x′)是一个支持向量机的核函数的充分必要条件为，当且仅当k(x)的傅里叶变化满足：

(8)

logistic型核函数的表达式为：

(9)

由(7)式可以看出logistic型核函数满足K(x,x′)=K(x-x′)。

logistic型核函数的傅里叶变化为：

(10)

因为式(10)中exp(-jwx)>0，1+exp(-ax2)>0，所以F[k(x)]≥0满足式(10)。

故logistic型核函数可以作为支持向量机的核函数。

当参数a的值分别取0.07、0.05、0.04、0.03，测试点为0时，logistic核函数图像如图2所示。从图2可以看出离测试点1越远的数据点受到的影响越大。从而说明了logistic核是一个全局性核函数，具有较好的外推能力，而且外推能力随参数a变化而变化。

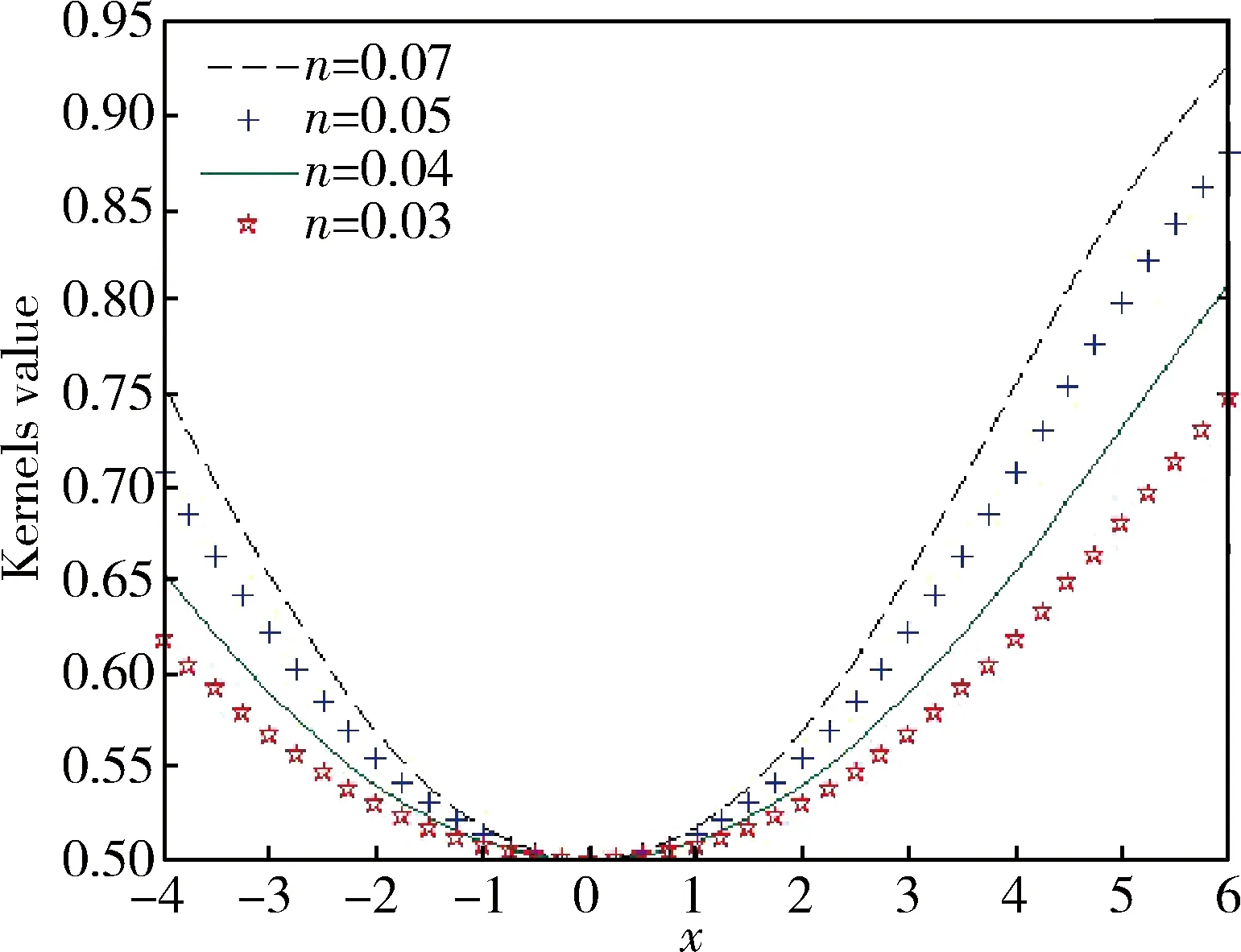
图2 logistic型核函数曲线图

4 一种混合核函数

国内外对支持向量机的核函数研究显示，任何支持向量机的核函数在某些方面都有它们的优点，也有各自的缺点与不足。不同核函数的支持向量机所表现出的学习能力、外推能力等差异性很大。总体而言，局部核函数的支持向量机因为相互之间距离较近的数据点对核函数的值产生影响比较大，所以容易产生过学习，而外推能力却不佳。全局核函数的支持向量机离测试点较远的数据对核函数的值影响较大，所以容易产生欠学习，但外推能力却比较好。鉴于这种情况，为了使支持向量机的学习能力和外推能力都比较好，所以选择用全局核函数和局部核函数来构造一种混合核函数的支持向量机，使之兼有局部核函数支持向量机学习能力强、全局核函数支持向量机外推能力强的优点。

通过对前面K型核函数和logistic核函数性质的分析，得到结论：K型核函数是一个局部核函数而且性能比传统的径向基核函数更好。logistic核函数是一个性能很好的全局函数。因此，受到启发，为得到性能较好的新的混合函数,将K型核函数与logistic核函数进行组合，构成一种新的混合核函数[6]。

引理2设K1和K2是在X×X上的核函数，X∈Rn，常数a≥0。则下面的函数仍是核函数[7]：

K(x,y)=K1(x,y)+K2(x,y)

(11)

K(x,y)=a×K1(x,y)

(12)

根据引理2，如果把两个性能不同的核函数进行线性组合，可以构造出新的核函数，如下所示，其中0≤n≤1。

K(x,y)=n×Ka(x,y)+(1-n)Kb(x,y)

(13)

所以构成新的混合核函数的表达式为：

K混合核=n×Klogistic核+(1-n)×KK型核

(14)

在图3中n分别取0.7、0.75、0.8、0.85，测试点为1，K型核函数中的K取1、m取1。从混合核函数的图中可以得出结论：新构造的混合核函数不仅具有K型核函数的特性而且还具有logistic型核函数的特性，测试点附近的数据以及离测试点较远的数据都对核函数的值产生很大的影响，所以由K型核函数和logistic型核函数构成的新的混合核函数的支持向量机的学习能力和外推能力都比传统核函数构成的支持向量机要优秀。

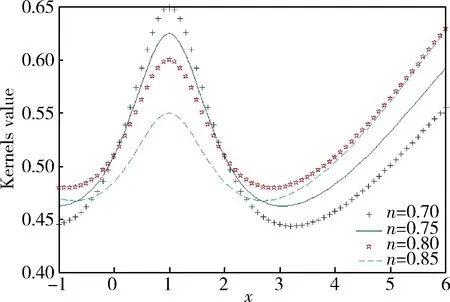
图3 混合核函数的曲线图

5 二维数据实验

输入两组数据，每组为50个。第一组数据点M是均值点为(0,0)、方差为1、标准差为1的正态分布的随机点。第二组数据点N是均值点为(2,2)、方差为1、标准差为1的正态分布的随机点。图4～图6分别为采用不同核函数支持向量机对两组数据的分类结果。

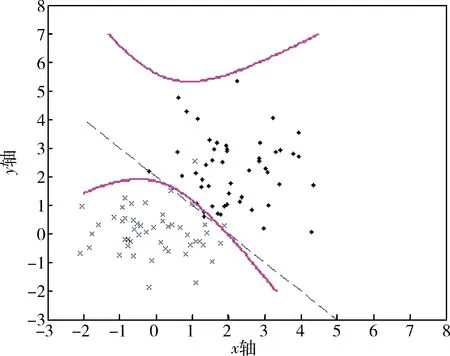
图4 多项式核函数的数据分类结果

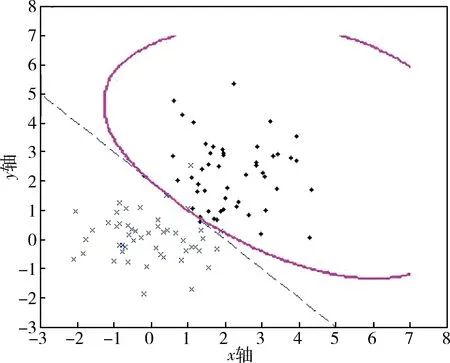
图5 高斯核函数的数据分类结果

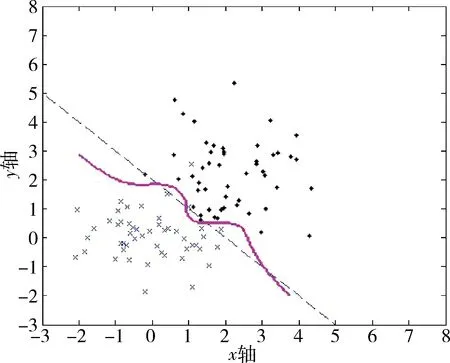
图6 混合核函数的数据分类结果

理论上M、N两组数据点的分类线为y=-x+2(图中虚线)，观察图4～图6可得：用传统的多项式核函数(全局核函数)和高斯核函数(局部核函数)的支持向量机，虽然能够将M、N两组数据点分类开，但其分类线与理论上的分类线相差甚远，这样当测试的数据点比较多时就会产生许多数据点分类错误，其精确性和泛化能力都不好。而采用K型核函数与logistic型核函数的混合核函数的支持向量机，其分类效果很好，基本接近理论分类线，其学习能力以及泛化能力都很优秀。

6 图片分类实验

将一组30张的汽车图片和一组26张的猫图片转换成256维的HSV数据。使用不同核函数的支持向量机对数据进行训练。将56张有汽车图片和猫图片转换成256维的HSV数据用作测试，如果是汽车图片则标记为1，如果是猫图片则标记为-1。如图7、图8所示。

图7 训练图片

图8 测试图片

测试结果：测试图片为30张汽车图片和26张猫图片，多项式核分类错了4张车图片和6张猫图片，准确率为82%；径向基核分类错了6张汽车图片和7张猫图片，准确率为76%；而K型核函数和logistic核函数的混合核函数分类错了3张汽车图片和3张猫图片，准确率为89%。图片分类结果表明，K型核函数和logistic型核函数的混合核函数的支持向量机图片分类准确率明显高于常用核函数的支持向量机。

7 结束语

本文提出了一种新型的支持向量机的核函数——K型核函数和logistic型核函数的混合核函数。分别分析了K型核函数和logistic型核函数的性能及其特点，将两者混合起来构造出新的核函数。从二维数据实验和图片分类结果上证明了新的混合核函数的支持向量机在分类效果、学习能力和外推能力方面均优于传统的多项式核函数和径向基核函数的支持向量机，具有良好的理论价值和应用价值。

[1] 丁世飞,齐丙娟.支持向量机理论与算法研究综述[J].电子科技大学学报,2011,40(1):2-10.

[2] VAPNIK V N. The nature of statistical learning theory[M]. New York: Springer-Verlag,1995.

[3] SAINI L M, AGGARWAL S K. Parameter optimization using genetic algorithm for support vector machine based price-forecasting model in national electricity market[J]. Genetation, Transmission&Distribution,IET,2010,4(1): 36-49.

[4] 孙翠娟.基于K型核函数的支持向量机[J].淮海工学院学报, 2006,15(4):4-7.

[5] HAMIDI S, RAZZAZI F, GHAEMMAGHAMI M P. Automatic meter classifycation in Persian popetries using support vector machine[C]. IEEE International Symposium on Signal Processing and Information Technology(ISSPIT).Ajman:2009, 563-567.

[6] 颜根廷,马广富,肖余之.一种混合核函数支持向量机算法[J].哈尔滨工业大学学报,2007,39(11):1704-1706.

[7] 徐立祥,李旭,吕皖丽,等.组合核支持向量机的模式分析新方法[J].计算机工程与应用,2013,49(24):112-115.

A kind of support vector machine based on hybrid kernel function

Liu Gaohui, Yang Xing

(School of Automation and Information Engineering, Xi’an University of Technology, Xi’an 710048, China)

In order to improve classification effect, learning ability and extrapolation ability of support vector machine, two kinds of kernel functions of support vector machine have been analyzed: K-type kernel function and logistic kernel function. A new support kernel machine with hybrid kernel function was constructed, and the performance of the new support kernel machine was analyzed in theory. The constructed support vector machines based on hybrid kernel function and the common kernel function were applied to handle the two-dimension data classification and images classification. Experimental results of two-dimension data points and image classification show that classification effect, learning ability and extrapolation ability of support vector machine based on hybrid kernel function are obviously superior to the support vector machine constructed by common kernel function.

K-type kernel function; logistic kernel function; hybrid kernel function

TP181

A

10.19358/j.issn.1674- 7720.2017.11.006

刘高辉，杨星.一种混合核函数的支持向量机[J].微型机与应用，2017,36(11)：19-22.

2017-01-15)

刘高辉(1968- )，男，博士，副教授，主要研究方向：信号处理。

杨星(1991-)， 男，硕士研究生，主要研究方向：机器学习。