关于误差椭圆教学内容设计的新思考
刘长建
(信息工程大学地理空间信息学院,河南 郑州 450052)
关于误差椭圆教学内容设计的新思考
刘长建
(信息工程大学地理空间信息学院,河南 郑州 450052)
误差椭圆既具有重要的实用价值又具有重要的理论基础意义。近些年来,误差椭圆的应用范围不断拓展,该部分内容在误差理论与数据处理课程中更加值得重视。为适应新的发展,本文对误差椭圆教学内容进行了新的思考与设计,从点位精度与误差椭圆、误差椭圆的概率意义、参数向量的假设检验3大部分进行了阐述。
误差椭圆;教学内容设计;新思考
误差椭圆一直是误差理论与数据处理教材中比较独立的章节[1-3]。传统的控制网优化设计与质量分析中,常常需要关注控制点的点位精度和某些特殊方向的点位精度,这一应用背景是教材中引入误差椭圆内容的一般出发点,基本教学内容如图1所示。

图1 误差椭圆基本教学内容
近些年来,误差椭圆除继续用于传统控制网优化设计与质量分析外[4],还用于GIS基本几何要素置信域与可视化研究[5]、卫星导航系统精度评估[6]、飞机导航性能实时评估与监视[7]、战场目标位置不确定性研究与可视化[8]、雷达定位精度分析和图形描述[9]、导弹落点误差分析[10]等多种场合,维数也拓展到三维甚至更高维。
误差椭圆既具有重要的实用价值,又具有理论基础意义。为适应新的发展,对误差椭圆教学内容进行了新的设计,分为点位精度与误差椭圆、误差椭圆的概率意义、参数向量的假设检验3大部分,下面分别加以阐述。
1 点位精度与误差椭圆
1.1 点位精度
主要内容可见文献[1—3],建议对点位方差的定义进行引申。点位方差的定义为
(1)
实际等价于
(2)

1.2 任意方向点位精度及其极值
为了便于向三维误差椭球乃至超椭球过渡,建议采用条件极值法推导任意方向点位精度及其极值,以下给出具体内容。
(3)
其中
(4)
(5)
对式(3)应用误差传播律,可得
(6)
其中
(7)
以上两式展开后即

(8)

(9)
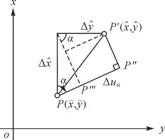
图2 任意方向α上的点位误差

由式(5)可知,向量s代表了α方向,是待求的方向向量。s的分量为α方向与x轴、y轴夹角的余弦,因此有
sTs=1
(10)
在满足此条件的前提下,求式(7)表示的quα的极值,可组成函数
式中,λ为未知联系数。令
可得
(11)
左乘sT,得
(12)
式(12)表明,quα的极值就是联系数λ。

可解得
λ为二重根。令
(13)
取
(14)
(15)

(16)
将解出的λ1、λ2回代到式(11)中,顾及式(5),便可解得σu的最大值、最小值方向及它们的方向向量,即

(17)
(18)

(19)
(20)
另外,由式(17)、式(19)还可以得出

(21)
式(21)是关于α1、α2的另外一种求法,但角度的象限判断比较麻烦。
以上就是按求条件极值的方法,推导任意方向点位精度极值的过程。要强调的是,向量s1、s2既是对应λ1、λ2的单位特征向量,又是使得任意方向点位精度取得最大值、最小值的方向向量。
另外,为讨论需要,对矩阵
(22)
作一简单分析。由线性代数可知,S为正交矩阵,且有
(23)
或
(24)
因s1、s2相互垂直,取α2=α1+90°并代入式(22),S还可以表示为
(25)
以上关于推导过程的建议,进一步加强了线性代数在本课程中的应用,如式(23)形式的矩阵谱分解,在近代平差理论中经常遇到。
1.3 误差椭圆及其方程
这部分通常先介绍误差曲线,再引入误差椭圆。建议:给出椭圆方程;规定长轴方向角的取值范围。
1.3.1 椭圆方程
在图3所示的ξPη坐标系中,误差椭圆方程形式最为简单,其标准形式为
(26)

图3 误差曲线与误差椭圆
(27)

(28)
式中,S矩阵即式(25)表示的S。
考虑到式(24),式(27)的左端还可以表示为
(29)
因此,xoy坐标系中误差椭圆方程为
(30)
类似的,误差椭圆也可以扩展到三维,即误差椭球。
1.3.2 长轴方向角的规定
高斯平面坐标由x轴方向到y轴方向的旋转构成左手坐标系,图3中ξ轴(长轴)方向到η轴(短轴)方向的旋转最好也采用左手坐标系。考虑到任意方向点位方差对称于P点,建议将α1限制在小于180°的范围内,短轴方向取为α1+90°,这样在利用式(17)求长轴方向时就规避了多值性问题,且不影响实际应用。
此外,由于数字化程度的提高,误差曲线的绘制不再是问题,建议将从误差椭圆量取有关量中误差的内容加以弱化,仅简要介绍做法。
以上建议体现了高等数学、线性代数相关内容在专业中的具体化应用,特别是对式(30)二次型表示的椭圆方程的理解,同时,也通过式(28)引入了坐标变换这一重要的基本知识点。
1.4 相对误差椭圆
这部分内容建议弱化从相对误差椭圆量取有关量中误差的内容,仅简要介绍做法。
2 误差椭圆的概率意义
2.1 置信椭圆
误差椭圆是图4中xoy面上同族的置信椭圆之一,平差点落入置信椭圆内的概率推导,可见文献[1—2]。在得出概率计算式
(31)
(32)

图4 二维正态分布密度曲面与置信椭圆

2.2 圆概率误差
在导航、军事等应用领域,经常使用圆概率误差(circular error probable,CEP)[13]。所谓圆概率误差,是以真实位置为圆心,随机点落入其中概率为β%的圆的半径,记为Rβ,常用的有R50、R90、R95等。
采用ξPη坐标系,圆概率误差可以描述为



(33)

类似的,圆概率误差的概念也可以扩展到三维,即球概率误差。
3 参数向量的假设检验
有了前述内容作基础,可以很容易理解式(30)的扩展含义。以间接平差为例,t维参数的超椭球为
(34)
点位落入超椭球内的概率表达式为
(35)
(36)
(37)
(38)

4 结 语
误差椭圆既具有重要的实用价值又具有重要的理论基础意义,是误差理论与数据处理课程的重点和难点之一。近年来,误差椭圆的应用范围仍在不断拓展,该部分内容在误差理论与数据处理课程中更加应该受到重视。
为适应新的发展,对误差椭圆教学内容设计进行了新的思考,主要有:更加突出了误差椭圆概率意义的讲解;采用了更易于向三维乃至多维扩展的推导方法;加强了椭圆二次型方程与标准二次型方程的转换与理解;引入了其他领域常用的圆概率误差;对从图上量取有关中误差的讲解进行了弱化;对误差椭圆长轴方向角的规定给出了建议。从知识的系统性角度,新的设计更加注重了概率论、线性代数、高等数学等课程知识在本课程中的应用,同时也考虑了向近代平差内容的过渡及与其他专业课程知识点的联系。
[1] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].3版. 武汉:武汉大学出版社,2015:194-209.
[2] 王穗辉.误差理论与测量平差[M].上海:同济大学出版社,2015:170-195.
[3] 隋立芬,宋力杰,柴洪洲.误差理论与测量平差基础[M].北京:测绘出版社,2010:140-177.[4] 吴俊昶,刘大杰,于正林.控制网测量平差[M].北京:测绘出版社,1998:87-97.
[5] 郭同德,王家耀,魏海平.GIS中基本几何要素的置信域问题研究[J].测绘学报,2003,32(2): 164-167.
[6] 张宇辛,卞鸿巍,王荣颖.一种基于误差椭圆的卫星精度评估方法研究[J].计算机与数字工程,2014,42(3): 364-368.
[7] 王丹,马航帅,孙晓敏.民用飞机导航性能实时评估与监视技术研究[J].航空电子技术,2014,45(4): 1-5.
[8] 卢代军,夏学知,张子鹤,等.目标位置不确定性的图形描述[J].火力与指挥控制,2006,31(9): 58-60.
[9] 陆捷,邵正途,向龙.无源雷达的二维定位精度分析和图形描述[J].火力与指挥控制,2011,36(2): 135-137.
[10] 李晓宇,田康生,郑玉军,等.基于关机点状态的弹道导弹落点估计及误差分析[J].舰船电子对抗,2014,37(5): 71-74.
[11] 黄维彬.近代平差理论及其应用[M].北京:解放军出版社,1992:457-494.
[12] 杨元喜.关于“新的点位误差度量”的讨论[J].测绘学报,2009,38(3): 280-282.
[13] 许丽丽,刘英乾,杨文彬,等.导航定位专业中几个与精度相关的术语辨析[J].导航定位学报,2014,2(3): 44-48.
New Thinking about the Design of Error Ellipse Teaching Contents
LIU Changjian
(School of Surveying and Mapping, Information Engineering University, Zhengzhou 450001, China)
Error ellipse is of important practical value and the theoretical basis of significance. In recent years, the application range of error ellipse is expanding, and the part in the error theory and data processing course is more worthy of attention. In order to adapt to the new development, new thinking on the error ellipse of teaching content and design are elaborated, from the positional accuracy and error ellipse, the meaning of the probability of error ellipse and the parameter vector of hypothesis test.
error ellipse; design of teaching contents; new thinking
刘长建.关于误差椭圆教学内容设计的新思考[J].测绘通报,2017(5):143-146.
10.13474/j.cnki.11-2246.2017.0175.
2016-05-06
国家自然科学基金(41374041)
刘长建(1973—),男,博士,副教授,主要从事误差理论和数据处理研究。E-mail: chxycj@163.com
G64
A
0494-0911(2017)05-0143-04

