虚部噪声辅助LCD方法及其在遥测振动信号处理中的应用

刘 学

(中国人民解放军91550部队 94分队，辽宁 大连 116023)

虚部噪声辅助LCD方法及其在遥测振动信号处理中的应用

刘 学

(中国人民解放军91550部队 94分队，辽宁 大连 116023)

针对局部特征尺度分解方法(Local Characteristic Scale Decomposition, LCD)的模态混叠以及集成局部特征尺度分解法(Ensemble LCD, ELCD)在集成平均时容易引入新的模态混叠、伪分量和运算量大等问题。提出一种基于虚部噪声辅助局部特征尺度分解法(Image Noise Assisted LCD, INALCD)；首先以原信号为实部添加虚部白噪声构成复数信号，然后对复数信号在指定方向上进行投影，求取对称投影象限的基函数，通过投影后虚部白噪声均匀化原信号投影的极值点的分布，辅助信号分解过程中极值点的选取，抑制模态混叠，最后将对称投影象限的基函数进行线性组合消除噪声的影响，避免了ELCD因集成平均带来的相关问题。仿真和实测数据实验结果表明，该方法在降低模态混叠的同时，大大减少了计算量，性能优于LCD和ELCD方法。

遥测振动信号；局部特征尺度分解方法；集成平均；模态混叠；投影；虚部噪声

遥测振动信号为典型的非平稳信号，叠加大量的高频、低频和冲击噪声，且当飞行器在飞行过程中发生异常或故障，振动信号中还将夹杂着各阶次的瞬态谐波分量，频域成分异常复杂，目前采用经验模态分解(Empirical Mode Decomposition, EMD)法[1]可以自动地将多分量信号分解为若干个分量，然后选择合适的分量进行分析，但EMD存在一些理论问题，如端点效应、IMF(Intrinsic Mode Function) 判据、没有快速算法和过包络等问题[2]。作为对EMD的改进，最近文献[3]提出了LCD(Local Characterstic Scake Decomposition)法，该方法能自适应地将一个多分量信号分解为若干个内禀尺度分量(Intrinsic Scale Component, ISC)之和。在减小拟合误差、降低计算量以及抑制模态混叠等方面的性能优于EMD方法，但在遥测振动信号的应用中，LCD的模态混叠问题依然严重，虽然ELCD(Ensemble LCD)和CELCD方法在一定程度上减轻了模态混叠，但是它也存在添加白噪声的幅值和集成平均次数的选择严重影响分解效果、容易产生过多的伪分量以及产生新的模态混叠等问题。针对以上问题，本文借鉴复数自适应分解算法的思想，提出了基于虚部噪声辅助局部特征尺度分解方法(Image Noise Assisted LCD, INALCD)，利用实部信号与虚部噪声之间的相关信息实现同步分解，将白噪声在指定方向上的投影均匀张成到不同尺度的原信号时频空间中，均匀原信号的极值分布，辅助极值点的选取，从而达到抑制了模态混叠的目的；同时添加的虚部噪声在求基线信号的过程中被消除，不产生噪声残留。仿真实验和实测信号分析表明：该方法可以有效地抑制模态混叠，性能优于ELCD方法，可以有效地对遥测振动信号进行分解和分析。

1 ELCD法

1.1 ISC判据和LCD法

LCD法可以将一个多分量信号自适应地分解为若干个ISC之和，各ISC分量相互独立，如果分量信号的任意2个极值点之间具有单一的模态，可称之为ISC分量，需同时满足以下两个条件：

(1)在信号的整个时间跨度内，相邻极值点符号互异，且任意两个相邻的极大值与极小值之间呈现单调性。

(1)

限于文章篇幅，LCD方法的具体流程请参见文献[3]，并对LCD与EMD算法进行了对比研究，证明了LCD在计算速度、拟合精度和抑制模态混叠等方面均优于EMD算法，但模态混叠问题仍然没有得到解决。

1.2ELCD法

为了抑制LCD法的模态混叠，文献[4]和文献[5]借鉴互补总体平均经验模态分解法(ComplementaryEEMD)[6]和完备平均经验模态分解法(CompleteEEMD)[7]的思想分别提出了ELCD法和CELCD法，通过成对的添加符号互异的白噪声到原始信号再集成平均分解，在均匀化原信号极值点分布的同时，较大程度的减少了白噪声在分解过程中的残留，提高了分解的完备性，由于CELCD和ELCD方法性能相当，本文只介绍ELCD方法，算法流程如下：

(1)在原信号x(t)中成对的添加符号互异的白噪声

(2)

式中：n(t)为均值为0，方差为1的高斯白噪声；λi为第i次添加白噪声幅值;N为添加白噪声对数，同时也是集成平均的次数。

(3)对所有ISC分量对进行集成平均，减弱添加白噪声在分解过程中的残留。

(3)

(4)

ELCD虽然在一定程度上抑制了模态混叠，但经过实验和分析，它也带来了一些新的问题，总结如下：

(1)由于添加的白噪声存在个体差异，在分解过程中因极值点的变化导致相同阶次的ISC分量的时频特性也会存在差异，虽然成对的添加白噪声和多次集成平均操作会减弱白噪声的影响，但其个体差异却会造成部分无法消除影响的累积，使信号的固有特征发生变化，进而导致相近尺度的信号出现在不同ISC分量中，造成新的模态混叠，作者分析这就是ELCD产生伪分量的主要原因。

(2)添加白噪声的幅值和集成平均次数对分解结果的影响较大，Wu等[8]在提出EEMD时给出了噪声幅值和集成平均次数的经验取值公式

(5)

ELCD也借鉴和继承了该经验公式，其中e为期望分解误差；ε为加入自噪声幅值标准差与原信号幅值标准差的比值，一般0.1≤ε≤0.5；N为集成平均次数。从式(5)可知，期望分解误差e与集成平均次数N成指数关系，如果想要降低期望分解误差，就必须大幅增加集成平均次数，这将极大地增加分解过程的运算时间。

2 噪声辅助复数局部特征尺度分解方法

经过上节的分析，针对ELCD存在的问题，借鉴复数经验模态分解[9]的思想，以原信号为实部添加虚部白噪声构成复数信号，利用实部与虚部之间的相关信息同步分解，就可以将原信号按其自身的时频特性自动投影到合适的参考坐标上，同时将白噪声在指定方向上的投影均匀张成到不同尺度的原信号时频空间中，均匀原信号的极值分布，辅助极值点的选取，从而达到抑制了模态混叠的目的。算法的具体流程如下：

步骤1 以原信号x(t)为实部添加虚部白噪声xn(t)=λn(t)构成复数信号，其中n(t)为均值为0，方差为1的高斯白噪声，λ=0.1～0.4×STD[x(t)]。

xc(t)=x(t)+ixn(t)

(6)

步骤2 将复数信号xc(t)投影到φmk上，然后取其实部，为了后续步骤消除噪声的影响，结合三角函数性质，将xc(t)均匀投影到四个象限，即φmk=αm+(k-1)×π/2, αm∈(0,π/2) k=1,2,3,4；m=1,2,…,Ne。这样总的投影方向数目为N=4Ne。

Pφmk(t)=Re[e-iφmkxc(t)]=x(t)cosφmk+xn(t)sinφmk

(7)

从式(7)可知，Pφmk(t)为x(t)在指定方向的投影加上幅值有限的白噪声，以三角函数进行比例缩放。这样白噪声在指定方向上的投影便均匀张成到不同尺度的原信号时频空间中，辅助极值点的选取，抑制模态混叠。

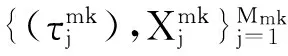
(8)

(9)

由于LCD采用线性插值求取基线信号，所有的运算均为线性运算，因此

(10)

(11)

从式(11)可知，虚部噪声在实部的投影可以辅助原信号极值点的选取，从而减小模态混叠。同时，噪声投影的影响在求基线信号的过程中被消除了，不产生噪声残留。

步骤4 将基线信号Lt从x(t)中分离出来，h1(t)=x(t)-Lt，若h1(t)满足ISC分量判据，则h1(t)为x(t)的第一个ISC分量ISC1(t)，否则将h1(t)作为原信号重复步骤1～步骤3，循环i次直至h1i(t)满足ISC分量判据，则ISC1(t)=h1i(t)。

步骤5 将ISC1(t)从x(t)中分离出来，即r1(t)=x(t)-ISC1(t)，以残余分量r1(t)作为原信号x(t)，采用排列熵(PermutationEntropy,PE)[10]检测x(t)是否包含高频间歇或噪声信号，具体方法和PE算法参数设置参见文献[4]，如果PE值大于阈值θ(θ∈[0.55, 0.6])，则认为x(t)是否包含高频间歇或噪声信号，令λ=0.1～0.4×STD[x(t)]；若PE值小于θ则认为x(t)不包含引起模态混叠的异常成分，令λ=0。重复步骤1～步骤4，重复循环n-1次，直到残余分量rn(t)为单调函数为止，得到

(12)

从算法的流程可知，INALCD只需一次分解，在每次迭代过程中仅需要投影方向个数次求基线函数的运算，经实验发现一般投影小于16个方向即可得到较为满意的分解结果。因此其计算量远远小于ELCD。

3 仿真和实测信号分析

3.1 仿真信号分析

设置2个仿真实验，采用易产生模态混叠的典型仿真信号对INALCD法、LCD和ELCD法的性能进行对比测试。

实验1 假设多分量信号x(t)包含2种信号成份，x1(t)=sin(2π80t) x2(t)=2sin(2π50t)，采样频率为1 000Hz。分别采用LCD、ELCD和INALCD对x(t)进行分解，其中ELCD集成平均次数为100次，每次添加幅值相同为0.3×STD[x(t)]的白噪声，INALCD采用4个投影方向α1=π/6，初始λ也设置为0.3×STD[x(t)]，结果如图1～图3所示。

从图1LCD的分解结果可知，在ISC1分量中出现了严重的模态混叠，同时包含仿真信号中80HZ和50Hz的频率成分，而ISC2和ISC3频率分别约为20Hz和10Hz，均为伪分量，这说明LCD发生了严重的模态混叠问题，不能对该仿真信号进行有效的分解；从图2可知，ELCD在一定程度上抑制了模态混叠，分解出了正确的ISC分量ISC3和ISC5，它们与真实分量的相关系数分别为0.959 2和0.963 3，但同时也产生了大量的伪分量，特别是产生了新的模态混叠分量ISC4，受模态混叠的影响，ISC3和ISC5分量能量也降低了，仅约为原分量x1(t)和x2(t)信号能量的50%。而图3INALCD完美的将仿真信号进行了分解，其ISC1和ISC2与真实分量的相关系数分别为0.986 4和0.991 7，而且在消除模态混叠的同时没有产生伪分量。

图1 实验1仿真信号及其LCD分解结果Fig.1 Emulate signal and its decomposition results by LCD in experiment 1

图2 实验1 ELCD分解结果Fig.2 Decomposition results by ELCD in experiment 1

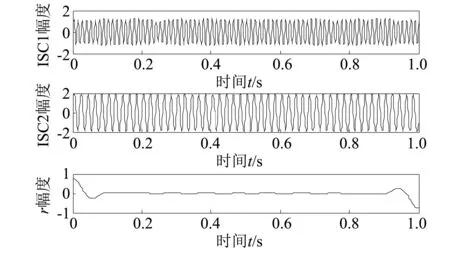
图3 实验1INALCD分解结果Fig.3 Decomposition results by INALCD in experiment 1

实验2 假设多分量信号x(t)包含3种信号成份，x1(t)为幅值分别为0.5和0.2频率为200 Hz的两段正弦信号组成的高频间歇信号，x2(t)=(1+t2)sin(40πt)，x3(t)=e-t/2sin(15πt)，采样频率为1 000 Hz。各算法的参数设置同实验1。结果如图4～图6所示。

从图4可知，对于包含间隙高频噪声的仿真信号，LCD没有分解出正确的ISC分量，分解失效；同实验1一样，在图5中，ELCD法分解出了正确的分量信号ISC4和ISC6，它们与真实分量的相关系数分别为0.983 6和0.945 4，但能量仅约为原信号的80%和50%，同时也产生了大量的伪分量，也产生了幅值较大新模态混叠分量ISC5。在图6中，INALCD虽然产生了伪分量ISC4，但分解出ISC2和ISC3两个正确的分量信号，它们与真实分量的相关系数分别为0.994 1和0.990 6。

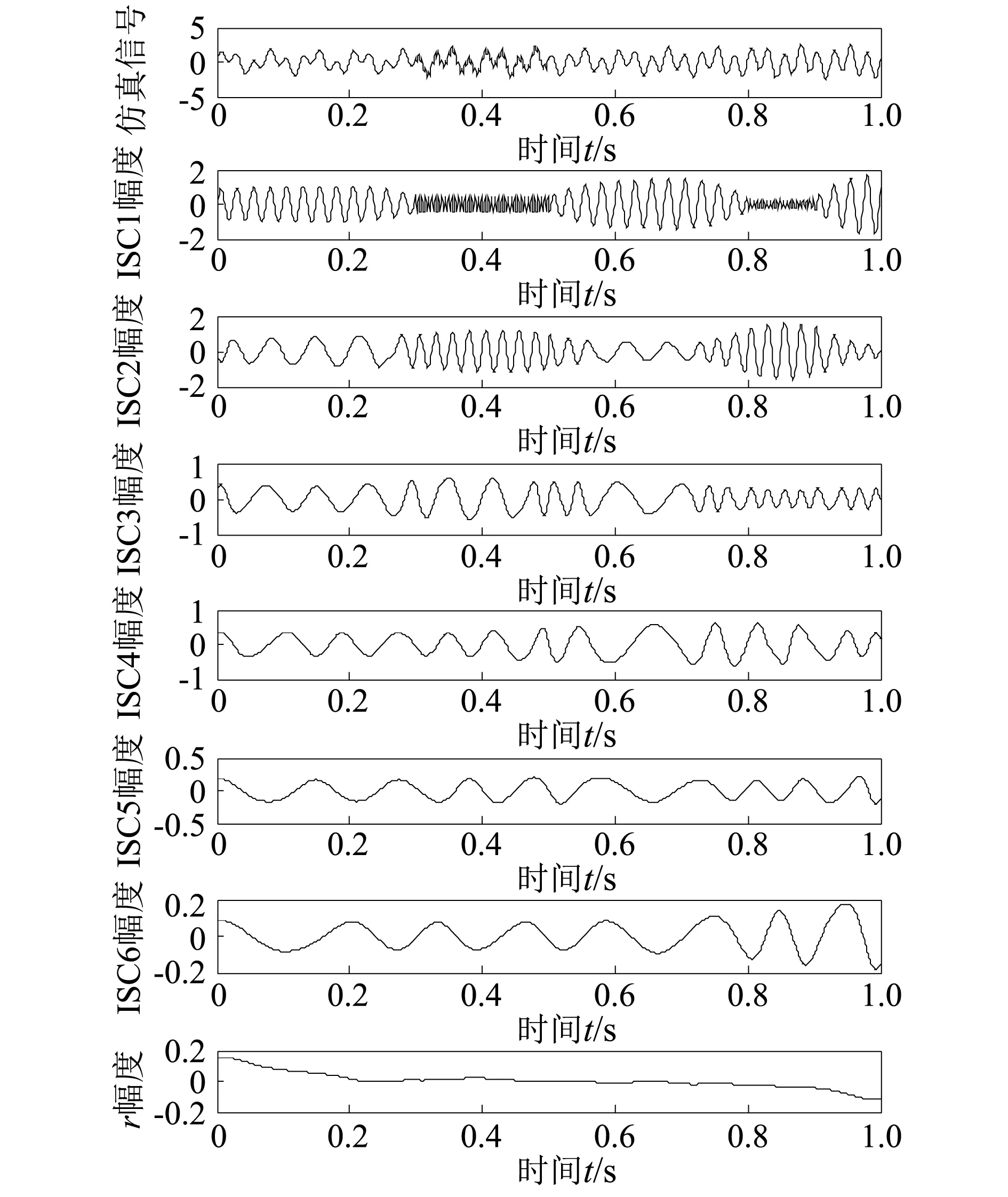
图4 实验2仿真信号及其LCD分解结果Fig.4 Emulate signal and its decomposition results by LCD in experiment 2

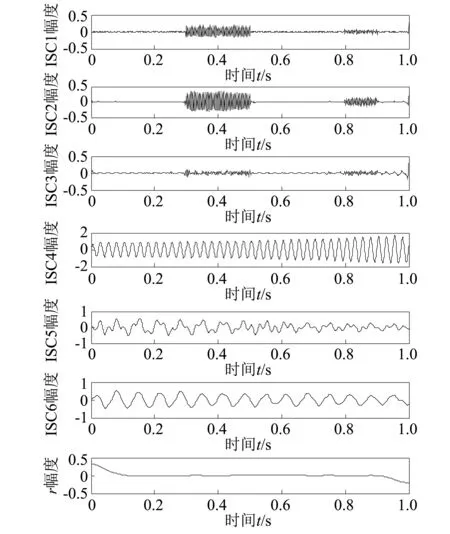
图5 实验2 ELCD分解结果Fig.5 Decomposition results by ELCD in experiment 2

图6 实验2 INALCD分解结果Fig.6 Decomposition results by INALCD in experiment 2

3.2 实测信号分析

采用某次飞行试验采集得到遥测振动信号对INALCD方法的性能进行检验，采样频率为5kHz，其中ELCD集成平均次数为120次，每次添加幅值相同为0.3×STD[x(t)]的白噪声，INALCD采用8个投影方向α1=π/12，α2=π/6，初始λ也设置为0.3×STD[x(t)]的结果，如图7～图9所示。

从图8和图9可知，INALCD分解出了正确的分量ISC3和ISC4，频率分别约为632Hz和414Hz，与前期飞行器振动台试验结果相一致，如图10所示，且频率混叠较小，仅产生两个伪分量ISC5和ISC6；而ELCD分解虽然分解出了正确的分量ISC3和ISC4，但分量能量衰减，且其中ISC3混叠较为严重，包含一些高频噪声和ISC4分量的成份，同时还分解出多达4个伪分量ISC5～ISC8。

图7 实测遥测振动信号Fig.7 The measured telemetry vibration signal

图8 实测信号的ELCD分解结果Fig.8 Decomposition results by ELCD of the measured telemetry vibration signal

图9 实测信号的INALCD分解结果Fig.9 Decomposition results by INALCD of the measured telemetry vibration signal

图10 振动台试验飞行器Z轴实测频谱Fig.10 Measured spectrum of aircraft Z-axis direction in Shaking table test

综合以上实验结果，可以得出采用LCD方法分解幅值与频率乘积相近和包含高频间歇噪声等信号时，易产生模态混叠问题；ELCD方法虽然可以分解出正确的ISC分量，但多次集成平均操作在导致计算量巨大的同时，每次添加噪声的个体差异会造成部分无法消除影响的累积，噪声的残留改变了信号的固有特征，导致相近尺度的信号在时频空间中发生混叠，进而产生新的混叠分量；INALCD采用添加虚部噪声然后均匀的投影到四个象限的方法，在均匀化原信号投影极值点分布的同时不产生噪声残留。因此可以得出结论，INALCD在抑制模态混叠，提高信号分解精度以、抑制伪分量以及提高计算效率等方面均要优于ELCD方法。

4 结 论

提出一种基于虚部噪声辅助局部特征尺度分解方法(INALCD)，采用易产生模态混叠的仿真信号和实测遥测振动信号对INALCD和ELCD的性能进行了对比分析，结果表明，相对于ELCD，INALCD至少存在以下优势：

(1)由于添加的虚部噪声投影在求基线信号的过程中被消除了，因此，INALCD不产生噪声残留，这就避免了ELCD因噪声个体差异造成无法集成平均消除的噪声累积，导致相近尺度信号出现在不同的ISC分量中进而产生新的模态混叠的问题。

(2)受集成平均的影响，ELCD分解的分量并不能保证满足ISC分量的定义，而INALCD方法得到的分量满足ISC分量判据，因此INALCD在保证分解分量的精确性方面要优于ELCD。

(3)因INALCD在每次迭代过程中仅需要投影方向个数次求基线运算，经实验发现一般选择投影小于16个方向即可得到满意的分解结果。避免了ELCD的集成平均操作，因此其计算量远远小于ELCD。

综上所述，INALCD在性能上优于ELCD方法，能较好地抑制LCD分解存在的模态混叠问题，可以有效地对遥测振动信号进行分解。

[1] HUANG N E, SHEN Z, LONG S R. The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis[J].Proceedings of the Royal Society of London, 1998，454(1):903-995.

[2] 黄林洲，郭兴明，丁晓蓉．EMD近似熵结合支持向量机的心音信号识别研究[J]．振动与冲击，2012，31(19): 21-25． HUANG Linzhou, GUO Xingming, DING Xiaorong. Heart sound recognition based on EMD approximate entropy and SVM [J]．Journal of Vibration and Shock，2012，31(19): 21-25．

[3] 程军圣，郑近德，杨宇.一种新的非平稳信号分析方法——局部特征尺度分解法[J].振动工程学报，2012, 25(2):215-220. CHENG Junsheng, ZHENG Jinde, YANG Yu. A new non-stationary signal analysis approach the local characteristic scale decomposition method[J]. Journal of Vibration Engineering, 2012,25(2): 215-220.

[4] 郑近德，程军圣，聂永红，等.完备总体平均局部特征尺度分解及其在转子故障诊断中的应用[J].振动工程学报，2014, 27(4):637-646. ZHENG Jinde, CHENG Junsheng, NIE Yonghong, et al. Complete ensemble local characteristic scale decomposition and its applications to rotor fault diagnosis[J]. Journal of Vibration Engineering, 2014, 27(4): 637 -646.

[5] 郑近德，程军圣，杨宇.部分集成局部特征尺度分解：一种新的基于噪声辅助数据分析方法[J].电子学报，2013, 41(5):1030-1035. ZHENG Jinde, CHENG Junsheng, YANG Yu. Partly ensemble local characteristic-scale decomposition: a new noise assisted data analysis method[J]. Acta Electrica Sinica, 2013,41(5):1030-1035.

[6] YEH J R，SHIEH J S. Complementary ensemble empirical mode decomposition: a noise enhanced data analysis method [J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156.

[7] TORRES M E, COLOMINAS M A，SCH-LOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C]∥ IEEE International Conference on Acoustics，Speech and Signal Processing. Prague: ICASSP，2011.

[8] WU Z, HUANG N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J].Advances in Adaptive Data Analysis, 2009, 1(1):1-41.

[9] RILLING G, FLANDRIN P，GONCALVES P. On empirical mode decomposition and its algorithms[C]∥ Proceedings of IEEE EURASIP Workshop on Nonlinear Signal and Image Processing. Grado: NSIP-03，2003.

[10] BANDT C, POMPE B. Permutation entropy: a natural complexity measure for time series[J].Physical Review Letters, 2002, 88(17):174102-1-4.

An image noise assisted Local Characteristic Scale Decomposition methodand its application in telemetry vibration signal processing

LIU Xue

(94 Units No.91550 Army, Dalian 116023, China)

In order to alleviate mode mixing in the Local Characteristic Scale Decomposition method (LCD), as well as solve the problem of the ensemble average always resulting in new mode mixing, illusive component, and computational cost increasing in the ensemble LCD (ELCD) method, an image noise assisted LCD method was proposed, First, a complex signal was formed by treating the original signal as the real part and adding white noise as the imaginary part. Then the complex signal was projected in the specified direction to strike the base functions of symmetrical projection quadrant. Through the projection of the imaginary part of white noise, the distribution of original signal extreme points were uniformed, the selection of extreme point was assisted in the decomposition. Finally, the quadrant projection was symmetrical linear combination of base functions to eliminate the effects of noise, which could avoid the problems associated by ELCD due to ensemble average. Experimental results show that the method can reduce mode mixing, while greatly reduces the amount of calculation. Its performance is superior to LCD and ELCD.

telemetry vibration signal; LCD(Local Characteristic Scale Decomposition); ensemble average; mode mixing; projection; image noise

2016-02-24 修改稿收到日期： 2016-05-05

刘学 男，博士，高级工程师，1983年生

Email:liuxue002@163.com

TN911.7

A

10.13465/j.cnki.jvs.2017.12.001