基于谱系聚类分析的桥梁结构模态参数自动化识别方法研究

徐 健， 周志祥， 唐 亮， 冉 杰， 何 杰

(1.重庆交通大学 土木工程学院，重庆 404100; 2.南充市住房和城乡建设局,637000; 3.西南交通大学 土木工程学院，成都 610031)

基于谱系聚类分析的桥梁结构模态参数自动化识别方法研究

徐 健1， 周志祥1， 唐 亮1， 冉 杰2， 何 杰3

(1.重庆交通大学 土木工程学院，重庆 404100; 2.南充市住房和城乡建设局,637000; 3.西南交通大学 土木工程学院，成都 610031)

桥梁结构模态参数识别作为桥梁健康监测系统的重要组成部分之一，对桥梁的长期健康监测具有重要意义。而现有的模态参数识别算法还不能实现结构系统阶次和模态参数的自动化识别，基于此，简单介绍了随机子空间算法的基本原理；通过引入“滑窗技术”以实现对时变结构模态参数的在线识别；针对稳定图定阶难这一问题，提出了基于奇异熵理论的系统定阶算法，以实现系统阶次的自动化确定；又将统计学中的“谱系聚类算法”与随机子空间算法进行结合，实现桥梁结构模态参数的自动化识别。利用该算法识别苏通大桥在竖桥向和横桥向的模态参数结果，并将其与理论计算值进行对比分析，结果表明：算法不仅能实现桥梁结构系统阶次的自动化确定，还能实现模态参数的自动化识别，方便对桥梁结构参数的实时监控，了解桥梁结构的健康运营状态。

桥梁结构；滑窗技术；随机子空间算法；模态参数；谱系聚类算法

桥梁结构模态参数识别[1]旨在反映桥梁结构固有的动力特性，是桥梁健康监测系统的重要组成部分，对桥梁长期的健康监测及营运安全具有重要意义。随机子空间算法(Stochastic Subspace Identification,SSI)[2]是目前较为广泛使用的桥梁结构模态参数识别算法，国内外学者已在SSI研究上已取得了较大成绩，但该算法在模型定阶和虚假模态识别上均以稳定图为依据，而稳定图中不具备各阶模态在结构响应中的贡献信息，导致无法获得在振动中占主导地位的模态；另外，稳态图中极点的选择主要通过人工完成，不仅工作量大、效率低，选择结果易受虚假模态的干扰，且还会因为选择者对模态识别的认知存在差异性，而导致识别结果存在一定的主观性[3]。综上，如何高效、准确的确定复杂系统或高阶大阻尼系统的系统阶次[4]，以及如何根据稳定图[5]来科学、有效的区分物理模态和虚假模态是模态参数识别当前亟需解决的问题。

针对SSI存在的一系列问题，本文进行了相应改进：首先通过引入“滑窗技术”以实现对时变结构模态参数的识别；其次，针对系统定阶难这一问题，提出了一种基于奇异熵理论的自动化定阶算法；最后为了实现模态参数的自动化识别，引入了统计学中的“谱系聚类算法”[6]，具体内容见下文。

1 数据驱动随机子空间算法原理

随机子空间算法SSI主要分为两大类，一类是基于协方差驱动的随机子空间算法(Cov-SSI)，另一类是基于数据驱动的随机子空间算法(Data-SSI)。通过对比分析两种算法的基本原理[7]以及两种算法的识别效果可知：Data-SSI算法在模态参数的自动化识别上具有明显优势，所以本文以Data-SSI算法为研究对象进行相应的改进。Data-SSI算法的实现步骤如下：

(1) Hankel矩阵的建立

首先利用结构的响应数据构造Hankel矩阵，具体的Hankel矩阵定义如下所示：

(1)

式中：Yp为“过去”输出行空间；Yf为“将来”输入行空间。

(2) 投影矩阵的计算

接着将“将来”输入行空间通过投影定理投影到“过去”输出行空间上，可以得到如下结果：

(2)

再对Hankel矩阵进行QR分解，可得到“将来”输入行空间到“过去”输出行空间的投影，结果如下：

(3)

“将来”输入行空间到“过去”输出行空间的投影Oi：

(4)

(3) 系统矩阵

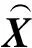
(5)

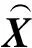
(6)

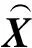
(7)

式子中：T为单位矩阵。

再利用数据驱动随机子空间算法对实际结构进行模态参数识别时，为了得到更好的分析结果，需要先对投影矩阵Oi进行加权处理，再进行SVD分解。

对上述中的Oi矩阵进行加权奇异值分解可得到如下结果：

(8)

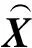
(9)

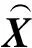
2 Data-SSI算法的改进

Data-SSI作为一种常用的结构模态参数识别算法，主要被运用于线性系统中，属于时域识别法，与其它的模态参数识别方法相比，该算法不需要参数化系统模型，只需要运用基本的矩阵分析方法，如QR分解、SVD分解等即可实现。但该算法依然存在以下三个方面的缺陷：

(1) 时变结构模态参数的识别：对于线性结构而言，Data-SSI算法能很好地识别出其对应的模态参数，但对于时变结构，Data-SSI算法的识别结果并不十分准确。主要原因在于：Data-SSI算法中涉及的状态空间模型是以线性时不变理论为基础，对线性结构具有很好的适用性，但当结构出现损伤时，其对应的结构状态便会发生时变，若继续使用基于线性时不变原理推导建立的识别方法求解结构模态参数，则识别的结果将会出现一定的误差。

(2) 系统阶次的自动化确定：系统的真实阶次难以确定，目前还没有统一的方法或者理论来确定系统的真实阶次。

(3) 模态参数自动化识别：目前稳态图中极点的选择常需要人为参与进行筛选，因为每个人专业水平残次不齐，在实际操作中会因为每个人极点的选择不同，导致模态参数识别结果存在差异性。

本文针对该算法存在的不足之处，提出了如下改进方法：

2.1 滑窗技术的运用

为了将随机子空间算法运用于识别时变结构，提出了一种“滑窗技术”，基本原理是：对结构响应信号进行合理地分段，当每个时段对应的时间足够短时，便可以假定在各时段窗口内该结构属于时不变系统，这样便能利用随机子空间算法对其进行模态参数识别。具体的算法步骤：

(1) 首先从起始时刻选取一条长度为N的时变振动信号Yi→i+N-1=[yi,yi+1,…,yi+N-1]，N>>0，由采样频率可知，此段长度为N的时变数据时长为ti→i+N-1=N/f，当ti→i+N-1足够小时，这段信号在此段时间内即可看作平滑的时不变信号。

(2) 利用Data-SSI算法对该窗口内的响应数据进行参数识别，假定该数据段的模态参数信息Mi=CSI(Yi→i+N-1)。

(3) 取递增步长为L，在前两步的基础上Yi+L→i+N+L-1=[yi+L,yi+L+1,…,yi+L+N-1]，N>>0，递归重复(1)、(2)两个环节的操作，得到Mi+L……Mi+L+N-1。

(4) 将步骤(3)所得到模态参数按照相对应的时间点绘于图上，即可得到该时变振动信号在整个时间段内的模态参数信息。

2.2 系统阶次的自动化确定

目前，常用的定阶方法是稳定图定阶，但其依然存在两方面的缺陷：

(1) 模态失真：主要是由外部因素所引起的不属于系统本身的模态，或者没有识别出系统本身具有的模态；

(2) 计算量大：主要是因为稳定图理论是以结构的频率、振型和阻尼等参数为判定稳定点的依据，所以需要计算出大量阶次下结构的模态参数。基于此，引入了奇异熵理论[8]以解决定阶难这一问题，该算法并不需要使用结构的模态参数进行稳定点的判定，这样便能在很大程度上减少计算工作量。以下就如何利用奇异熵进行系统定阶进行详细分析：

(1) 通过信号奇异值分解原理[9]可知，对于一个m×n维的实矩阵Q，可以被分解为一个m×l的矩阵R、一个l×l维的对角线矩阵Λ和一个n×l的矩阵S，且四者间存在如下关系：

(10)

通过分析矩阵Λ中的主对角元素λi(矩阵Q的奇异值)可知，主对角元素的多少与信号所含频率成分的复杂程度有着密切的联系。当主对角线上元素越多时，则说明原始信号成分越复杂；当原始信号受到噪声干扰时，主对角元素有可能均为非零值，即表明原始信号的频率成分越简单。根据这一特点，可以利用Λ矩阵对振动信号的信息量做出客观反映，奇异熵定义式为

(11)

式中：k为奇异熵的阶次；ΔEi为奇异熵在阶次i处的增量。

通过分析式(11)可知，随着阶次的不断增加，奇异熵的增量会逐渐降低最后趋于稳定，且这一特性不随信号的外界干扰程度发生改变。因此可将奇异熵的增量作为系统阶次的判断标准，即当奇异熵的增量趋于稳定时，此时对应的阶次就为系统的真实阶次。实际操作中，可以对奇异熵的增量求一阶导数，当导数值趋于0时，表明奇异熵的增量趋于稳定，此时对应的阶次即为系统的真实阶次。

利用奇异熵增量一阶导数进行系统定阶的优点在于：不需要利用结构的模态参数来判定稳定点，这样便能在很大程度上减少计算工作量、提高效率、增加判定可靠度。

2.3 模态参数自动化识别

利用Data-SSI算法进行模态参数识别，除了系统定阶外，另外一个难题就是对物理模态的拾取。传统的拾取方法主要依靠工作人员观察稳定图来完成，这样不仅工作效率低，同时还会因为个人认知水平存在差异，而导致识别的结果存在主观性。

实际工作中，虽然各时刻传感器采集的响应信号都会受到不同程度的外界因素影响，但信号内部始终会包含该桥梁结构的结构信息。因此对于一座桥梁结构而言，在短时间内，其模态参数是不会发生较大变化的，即真实模态在这一时刻的稳定图与下一时刻的稳定图中均会存在，只有虚假模态会发生变化。根据这一特性，可以先利用“滑窗技术”绘制出时间段相邻的若干幅稳定图，再对这些稳定图进行筛选，以便分辨出结构的真实模态。但在实际操作中，如果只是依靠人工逐一对相邻时间段的多幅稳定图进行筛选，不仅费时费力，同时还会因为个人认知能力的差异导致筛选出的真实模态存在主观性，再加上数据量极其庞大，实际工作中几乎无法利用人工操作这一方式实现对真实模态的筛选。基于此，引入了统计学中的谱系聚类法[10]来实现对真实模态的自动化筛选，以达到模态参数自动化识别的目的。以下就如何实现模态参数自动化识别的步骤进行详细分析：

(1) 结构信号的筛选和分组

利用探索性数据分析方法对各传感器采集的结构响应信号进行分析，绘制结构信号对应的直方图，选取满足正态分布的结构信号作为模态参数识别算法的输入数据；利用“滑窗技术”对传感器采集到的桥梁结构信号进行合理时段划分，假定结构信号共分为N组。

(2) 系统阶次的确定

对满足正态分布的结构信号进行奇异值分解，再利用2.2节的算法确定桥梁结构的真实阶次，并用字母n表示。

(3) 稳定图阶次范围确定

确定稳定图绘制的阶次范围为[1,2n]，即从系统的第1阶开始计算，最大计算阶次为2n。

(4) 模态参数的识别

利用Data-SSI对N组结构信号进行模态参数识别，得到N组识别结果，每组结果都包含对应的频率值、阻尼比以及振型系数。

(5) 距离矩阵的建立

假定N组识别结果自成一类，即可以建立N个子集，分别用X1,X2,…XN表示，每组结果中都包含频率、阻尼比和模态振型。从第一个子集开始，依次计算第i个子集与第i+1个子集之间的距离(相似性)，得到n×n维的距离矩阵D(i)，n为系统的真实阶次。

为了建立距离矩阵，需定义能够反映模态之间距离的统计量，鉴于稳定图是由固有频率、阻尼比以及模态振型所构成，因此用这三个参数作为聚类因子，定义模态i和模态j之间的距离dij，计算公式为

(12)

式中：df、dξ、dψ分别代表频率、阻尼比和模态振型的容差，根据文献[10]确定各容差的取值为：df=0.01、dξ=0.05、dψ=0.02。其中的wf、wξ、wψ分别代表频率、阻尼比以及模态振型在模态距离计算中的权重，且三者之和为1。因本文的侧重点在于识别出精确的频率值，因此本文频率对应的权重值较另两者考虑得大，本文取wf=0.4、wξ=0.3、wψ=0.3。

(6) 同类项的聚类

1) 通过第(5)步可以求得第k组结果与第k+1组结果的距离矩阵D(k)。

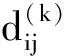
3) 依次将第k组结果和第k+1组结果中所有同类的模态都聚为一类，再与其它剩余的模态建立一个新的子集Xk+1。

4) 按照相同的原理将步骤3)中所得的子集Xk+1与子集Xk+2进行聚类，并再次构建新的子集Xk+2；接着再将其与子集Xk+3进行聚类，依次类推，直到将N个子集都聚类完成，得到最后的新子集XN。

5) 统计新子集XN中每阶模态的聚类元素的个数，根据文献[10]可知：当聚类元素的个数大于0.6n(n为系统的真实阶次)时，则认为该模态为真实模态，并将其绘制于稳定图中。

基于滑窗技术、奇异熵增量导数定阶以及谱系聚类算法的桥梁结构模态参数自动化识别的基本流程图,如图1所示。

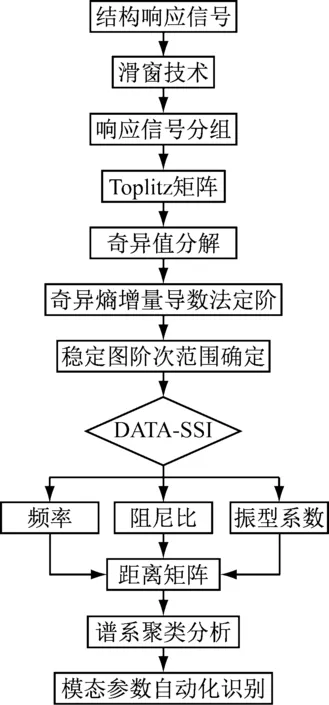
图1 模态参数自动化识别流程图

3 苏通大桥模态参数在线自动化识别

现以苏通大桥为研究对象进行模态参数在线自动化识别，并将识别结果与桥梁的真实结果进行对比分析，具体步骤如下：

(1) 首先利用探索性数据分析方法对各传感器采集的结构响应信号进行分析，筛选出满足正态分布的的结构信号。

(2) 对筛选出的结构信号利用“滑窗技术”进行信号分组，以满足Data-SSI算法的基本要求，再对响应数据进行奇异值分解，并根据2.2节所提算法进行系统阶次的确定。

(3) 利用Data-SSI算法对响应信号进行模态参数识别，得到多组识别结果。

(4) 然后利用2.3节介绍的谱系聚类分析实现模态参数的自动化识别。

(5) 最后将自动化识别结果与真实结果进行对比分析，以验证本文算法的可靠性。

3.1 工程概况

苏通大桥是主跨为1 088 m的双塔索面斜拉桥，具体的跨径布置为(2×100+300+1 088+300+2×100)m。该桥属于大型斜拉桥，在建造时设计了一套完整的健康监测系统，能够时时监测该桥梁的运营状态，评估其使用性能。该桥上共布置了多种类型的传感器，包括温度传感器、索力传感器以及加速度传感器等，采样频率为20 Hz。本文选取主桥上14个加速度传感器的实测竖向响应信号进行模态参数识别，加速度传感器的布置,如图2所示。

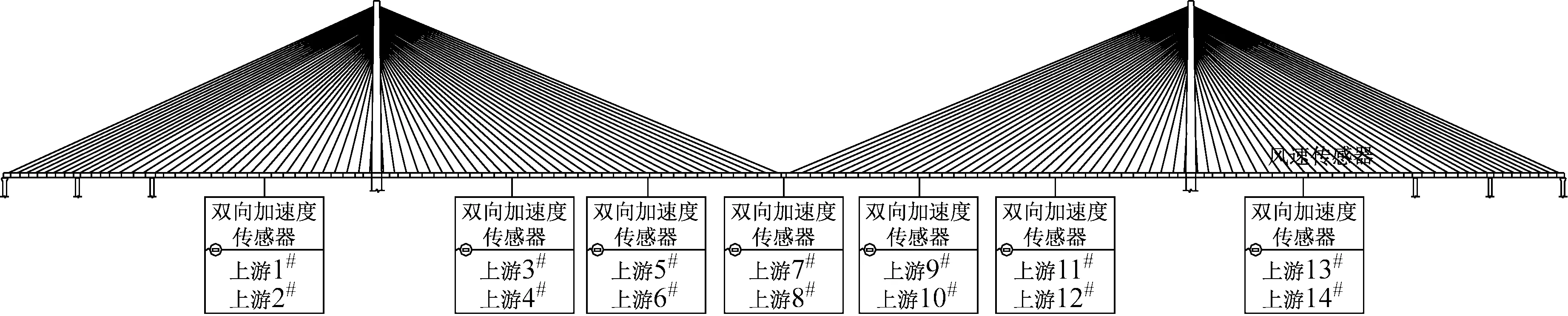
图2 加速度传感器布置图

3.2 结构响应信号筛选

该桥梁结构的健康监测系统能够实现全天候不间断数据采集，数据量庞大，如果对全年的响应信号进行分析，则工作量很大。鉴于此，本文按四个季度分别进行分析，且每个季度仅选一个具有代表性的月份进行分析，这样便能以较小的工作量来实现对苏通大桥整年运营状态的监测。各季度选取的月份为：春选3月份、夏选7月份、秋选10月份、冬选12月份。利用探索性数据分析方法中的直方图法对上述4个月份的加速度响应信号进行分析，图 3罗列了7月份14个传感器采集响应信号对应的直方图。根据该图可知：第2个传感器采集的结构响应信号并不满足正态分布，即只能使用其它13个传感器采集的响应信号进行参数识别。

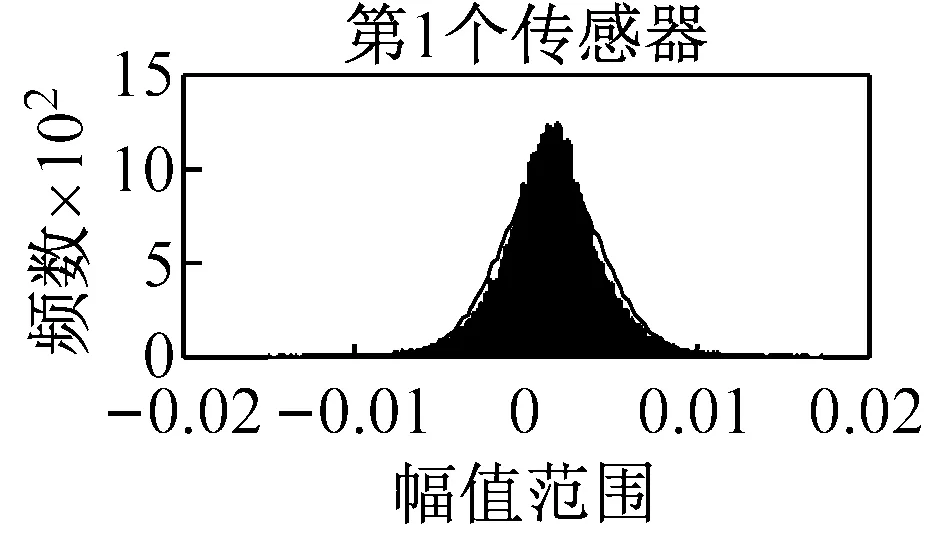
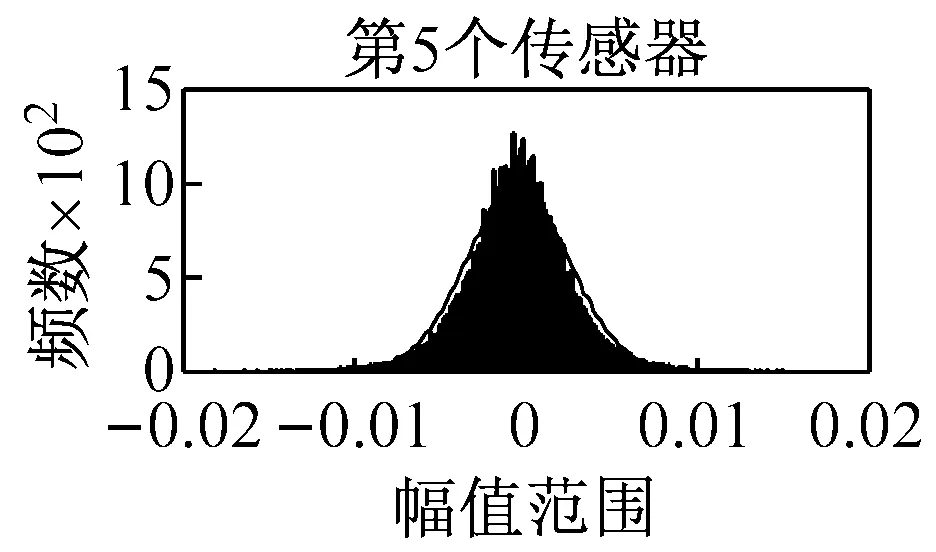
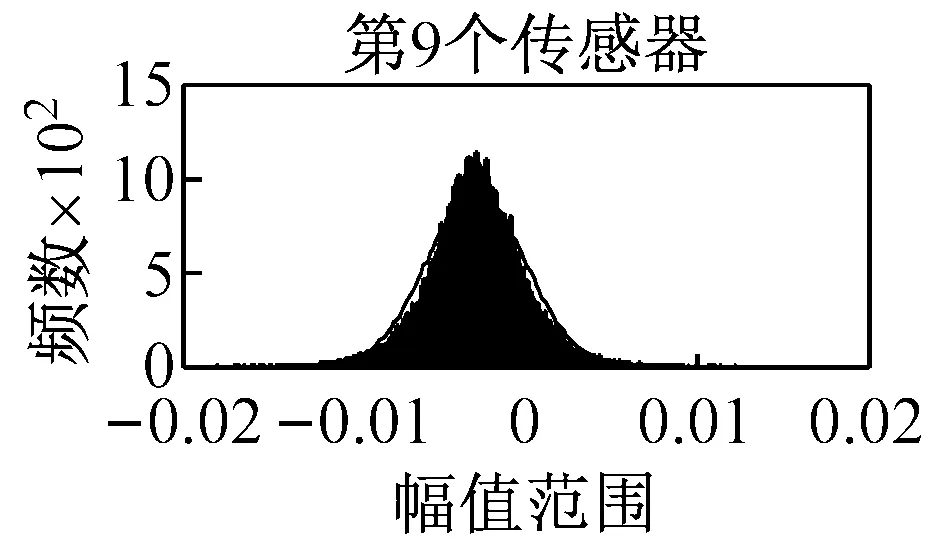
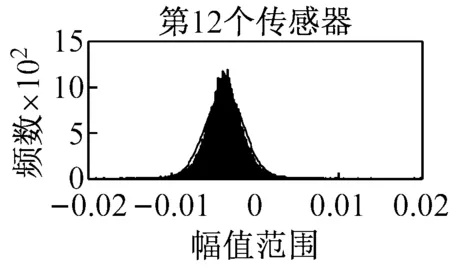
3.3 响应信号的分组

考虑到苏通大桥对应的模态参数结果会随着时间的推移出现细微的变化，但却不会在短时间内发生变化。鉴于此，本文以“每小时”为单位，即“滑窗技术”中的窗口长度选择1小时对应的数据长度为一窗，在每个窗口内该桥梁结构属于时不变结构，这样便可运用随机子空间算法对其进行模态参数识别。需要注意的是：以“1小时”的数据作为参数识别的输入，即每次每个传感器输入的数据量为72 000个数据，由于该桥梁结构上共有13个有效传感器，即每次参数识别时输入的数据矩阵为72 000×13。对每个时间窗口进行模态参数识别，便能获取该桥梁结构模态参数随时间的具体变化情况。

3.4 奇异熵增量法定阶

对每个窗口内的结构信号进行奇异值分解并计算相应的奇异熵，接着绘制出系统阶次与奇异熵增量的变化走势图，见图4。为了更为直观地判别奇异熵的增量是否稳定，对其求一阶导数，得到奇异熵增量斜率变化走势图，见图5。对比两图不难发现：通过观察奇异熵增量的一阶导数能更有效地获取系统的真实阶次，根据图中数据走势情况可知，当系统阶次为150阶时，奇异熵增量趋于稳定，此时奇异熵增量的一阶导数趋近于零，即可判定苏通大桥的真实系统阶次为150阶。

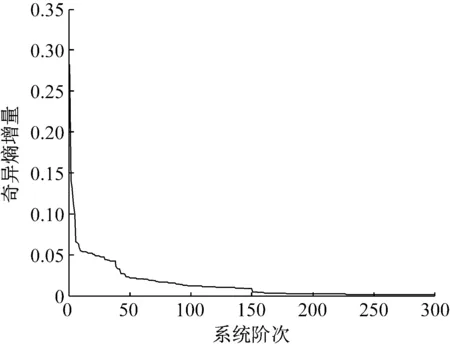
图4 奇异熵增量走势图

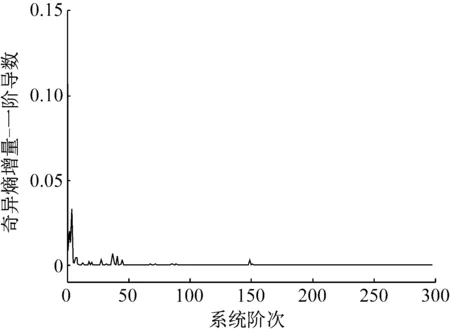
图5 奇异熵增量斜率走势图

3.5 竖桥向模态参数识别结果对比分析

本文选择7月1日对应的竖向振动信号为研究对象，按单位窗口长度将该天的信号数据分为24组，以下就这一天前2个小时的稳定图进行对比分析，结果见图6和图7所示。由图可知：该桥梁结构属于高阶系统，如果仅仅依靠一幅或者两幅稳定图来区分虚假模态和真实模态，所得结果可能会出现较大偏差。通过分析多幅稳定图可以发现：真实模态在多幅稳定图中均会存在，且其对应的稳定轴稳定性较好，而虚假模态只会在少数稳定图中存在，且其对应的稳定轴稳定性差。为进一步获得该桥7月份第一天的真实模态，现运用2.3节提出的自动化识别算法对这一天24小时对应的24组模态参数结果进行谱系聚类分析，聚类结果如图8所示。由该图可知：对多组识别结果先进行谱系聚类分析再绘制稳定图，不仅能够很好的剔除虚假模态，保留真实模态；还能有效避免因人为筛选真实模态带来的主观性。

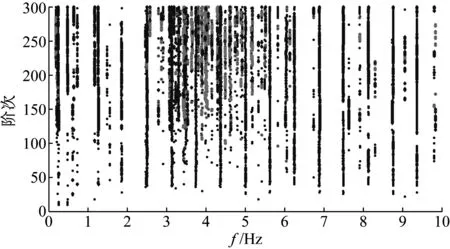
图6 竖桥向稳定图(第1个小时)

Fig.6 Stability diagram in vertical direction (The first hour of a day)

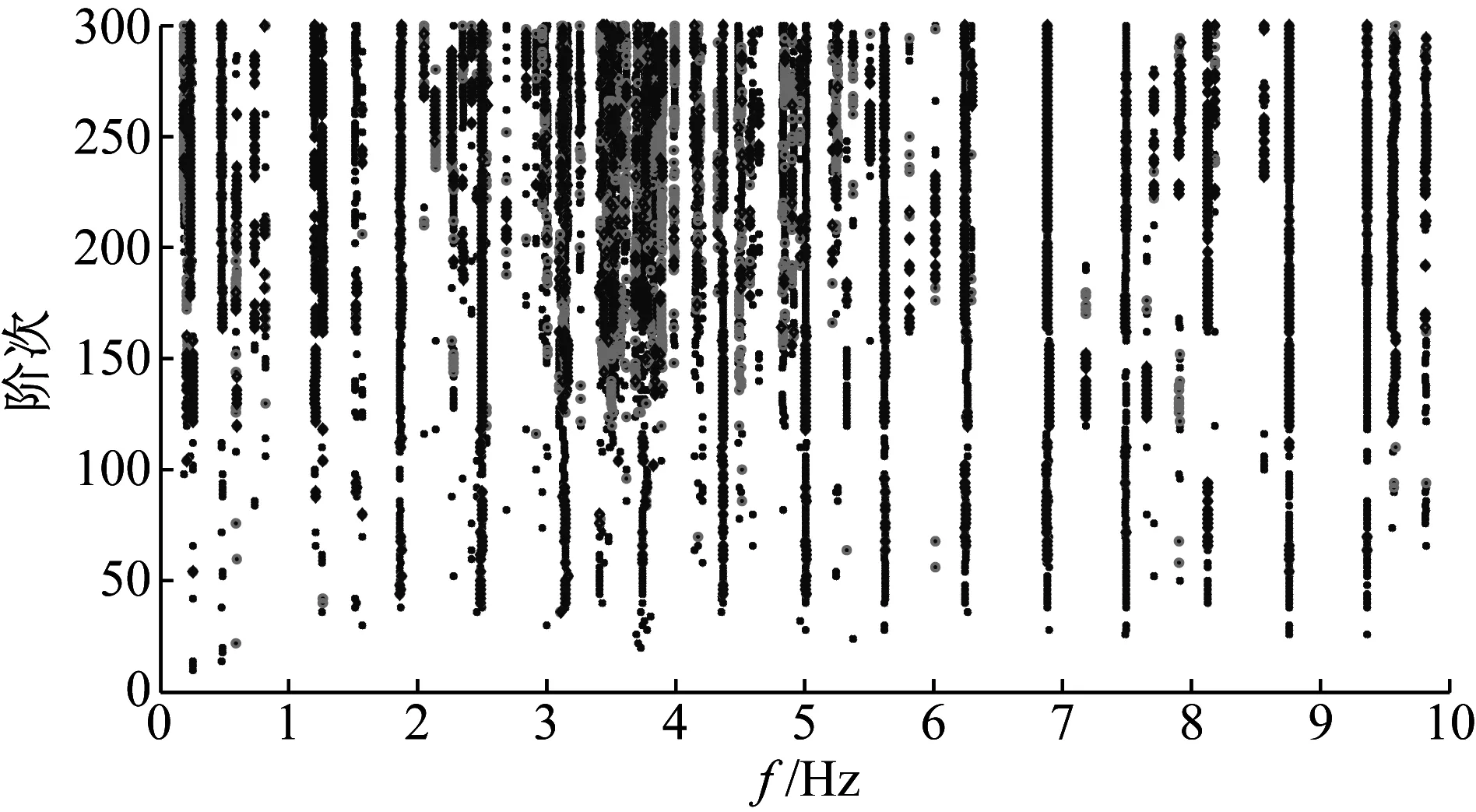
图7 竖桥向稳定图(第2个小时)

Fig.7 Stability diagram in vertical direction (The second hour of a day)

为进一步验证本文算法识别结果的可靠性，将识别得到的竖桥向前5阶频率值与文献[11]中给出的竖桥向频率理论计算值进行对比分析，具体结果见表3。根据表中数据可知：本文算法识别的频率值与理论计算值基本吻合，误差在0～5%间，能够满足工程需求，即本文所提算法能准确、可靠的实现桥梁竖桥向模态参数的自动化识别。

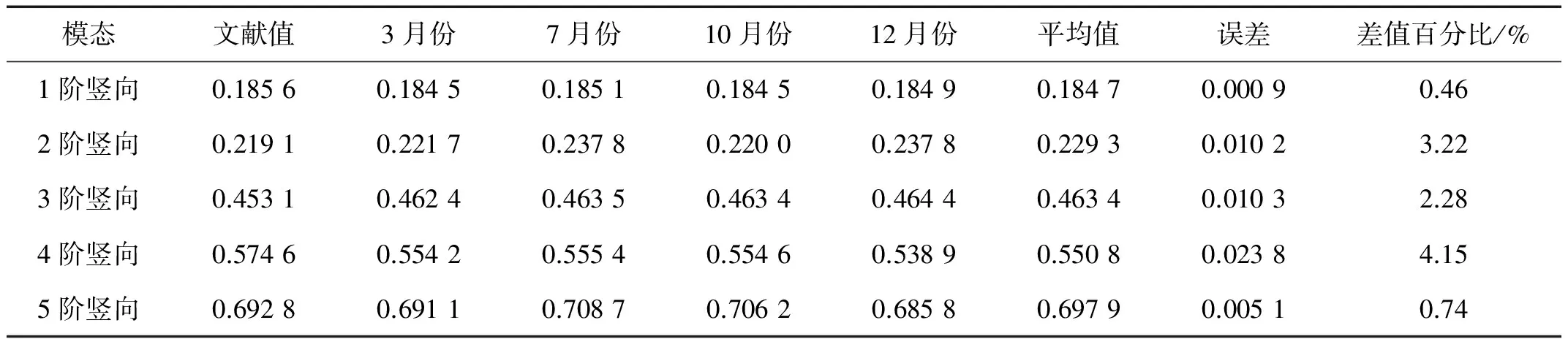
表3 竖桥向频率结果(Hz)

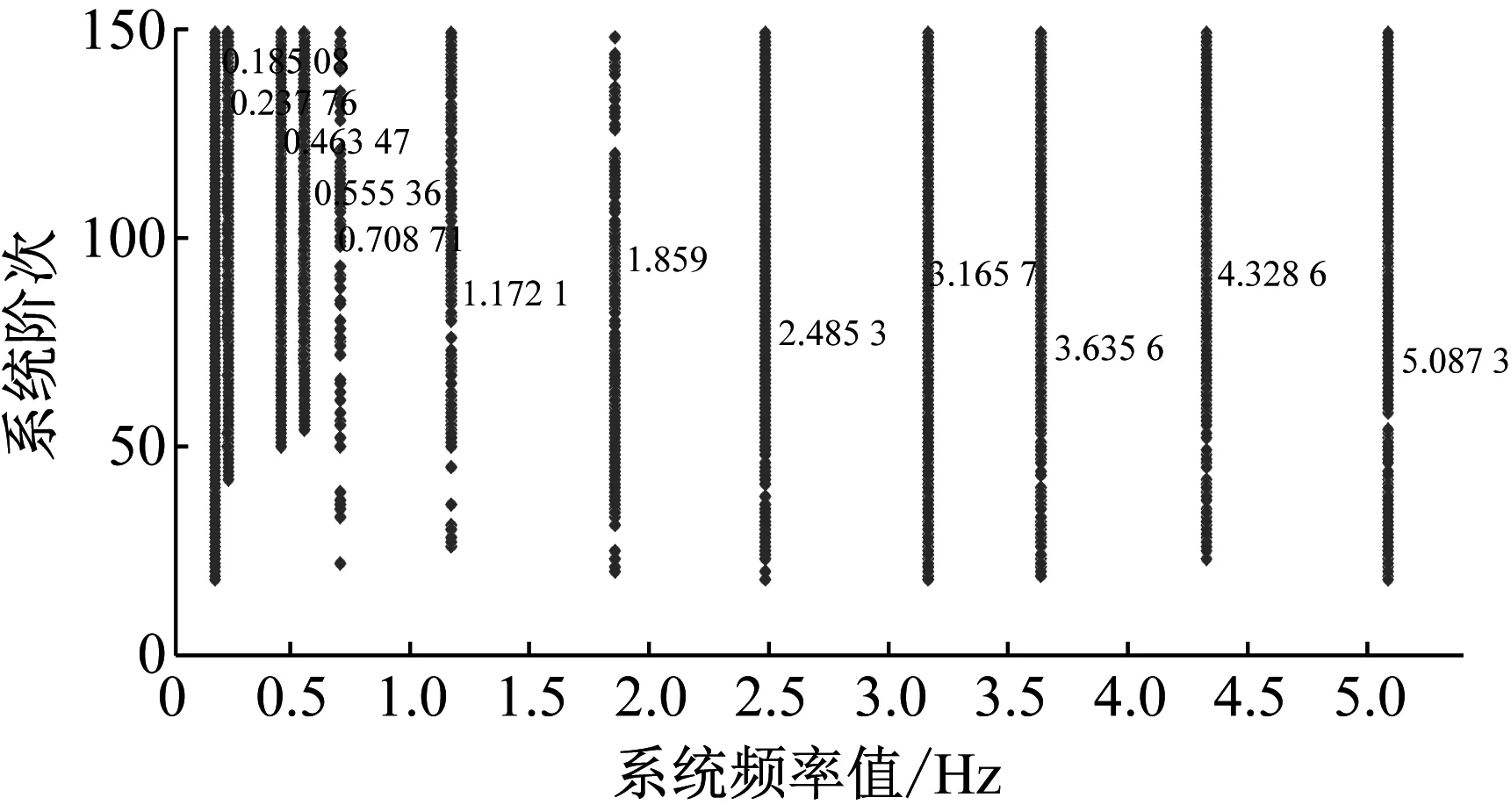
图8 竖桥向聚类稳定图(7月1日)

Fig.8 Stability diagram of hierarchical clustering in vertical direction(The first day of July)

图9是本文算法识别得到的该斜拉桥前3阶模态振型图，由图可知：前3阶模态振型图与实际振型图很相似，相似度在95%左右，进一步验证本文算法的可行性。

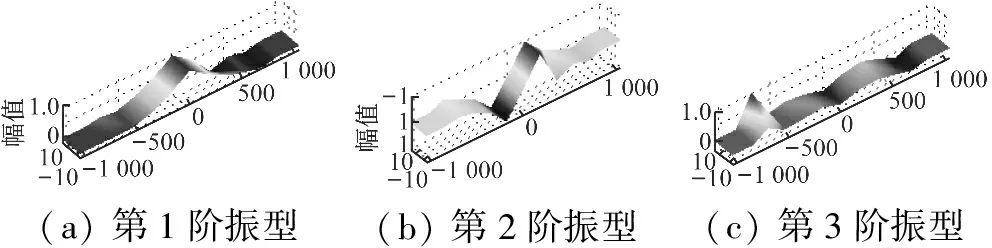
(a)第1阶振型(b)第2阶振型(c)第3阶振型

图9 竖桥向前3阶振型图

Fig.9 Vibration diagram of former three orders in vertical direction

为了研究该桥梁结构竖桥向前5阶频率值在各季度的具体走势情况，识别出了该桥梁结构在3、7、10以及12月份共124天对应的频率值，并绘制了各阶频率值随时间变化的走势图，见图14所示。根据该图可知：在2015这一年时间里，该桥梁结构的第1阶和第2阶频率值基本处于稳定状态；其它3阶频率值随着时间变化出现波动，但波动范围很小。基于桥梁结构的模态参数能够反映其固有的动力特性这一理论，可知：苏通大桥在2015这一年时间里竖桥向的动力特性处于稳定状态，即该桥梁结构在竖桥向运营状态良好。

3.6 横桥向模态参数识别结果对比分析

为进一步验证本文算法的通用性，现利用竖桥向模态参数的识别流程对识别出了横桥向对应的模态参数。图11是苏通大桥在2015年7月1日第1个小时横桥向对应的稳定图，图12是第一天24小时对应聚类稳定图。对比两图可知：聚类稳定图能够很好的剔除虚假模态，并保留真实模态。同时为了进一步验证横桥向识别结果的精确性，将识别得到的横桥向前5阶频率值与文献[11]中给出的横桥向频率理论计算值进行对比分析，具体结果见表4。根据表中数据可知：本文算法能实现横桥向模态参数自动化识别，且识别得到的频率值与理论计算值很接近，误差在0～10%间。

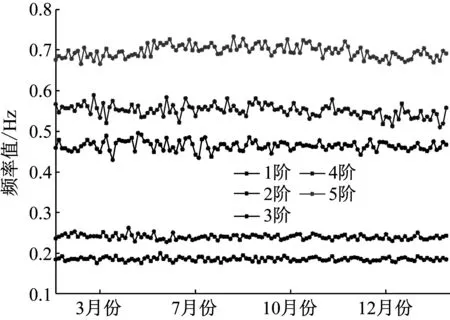
图10 竖桥向前5阶频率值

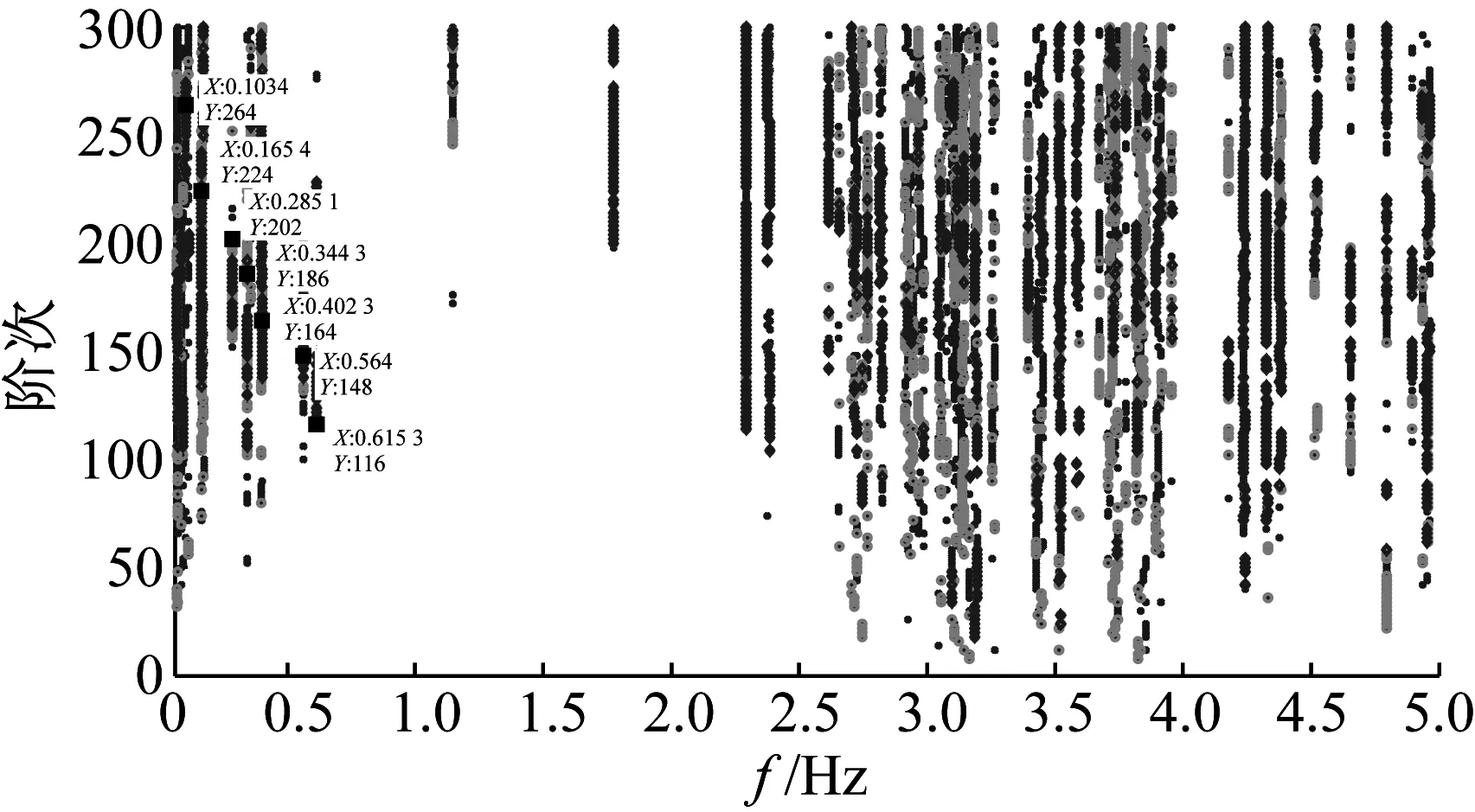
图11 横桥向稳定图(第1个小时)

Fig.11 Stability diagram of transverse direction (The first hour of a day)

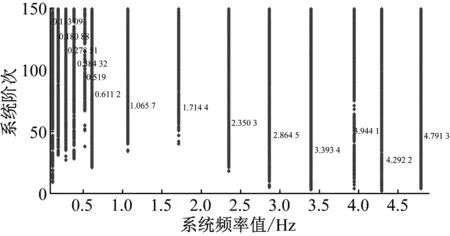
图12 横桥向稳定图(7月1日)

Fig.12 Stability diagram of transverse direction (The first day of July)

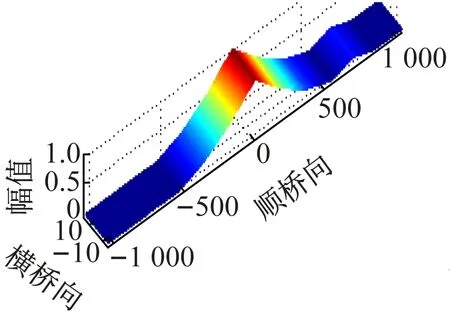
(a) 第一阶振型

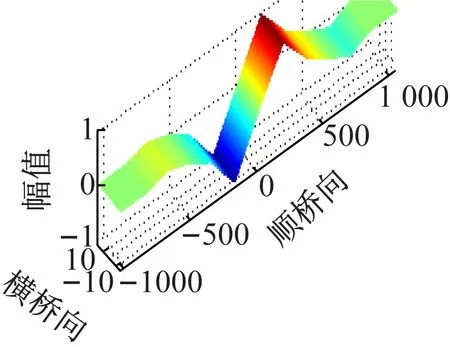
(b) 第二阶振型

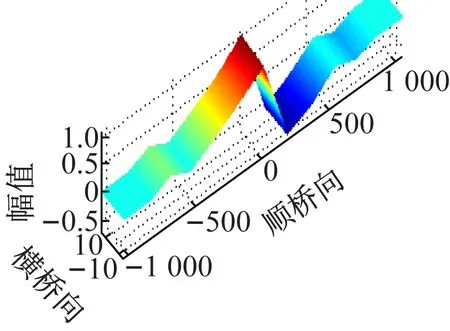
(c) 第三阶振型

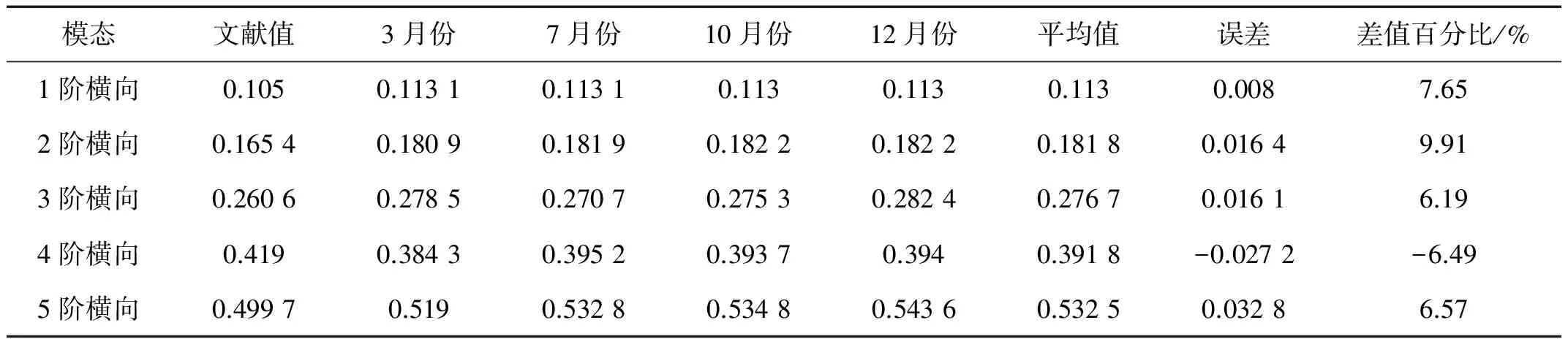
表4 横桥向频率结果

为了研究苏通大桥横桥向前5阶频率值在各季度的具体走势情况，识别出了该桥梁结构在3,7,10以及12月份共124天对应的频率值，并绘制了各阶频率值随时间变化的走势图，见图14所示。根据该图可知：在2015这一年时间里，横桥向前5阶频率值基本处于稳定状态，表明：苏通大桥在整个一年时间段里横桥向的动力特性处于稳定状态，桥梁结构运营状态良好。

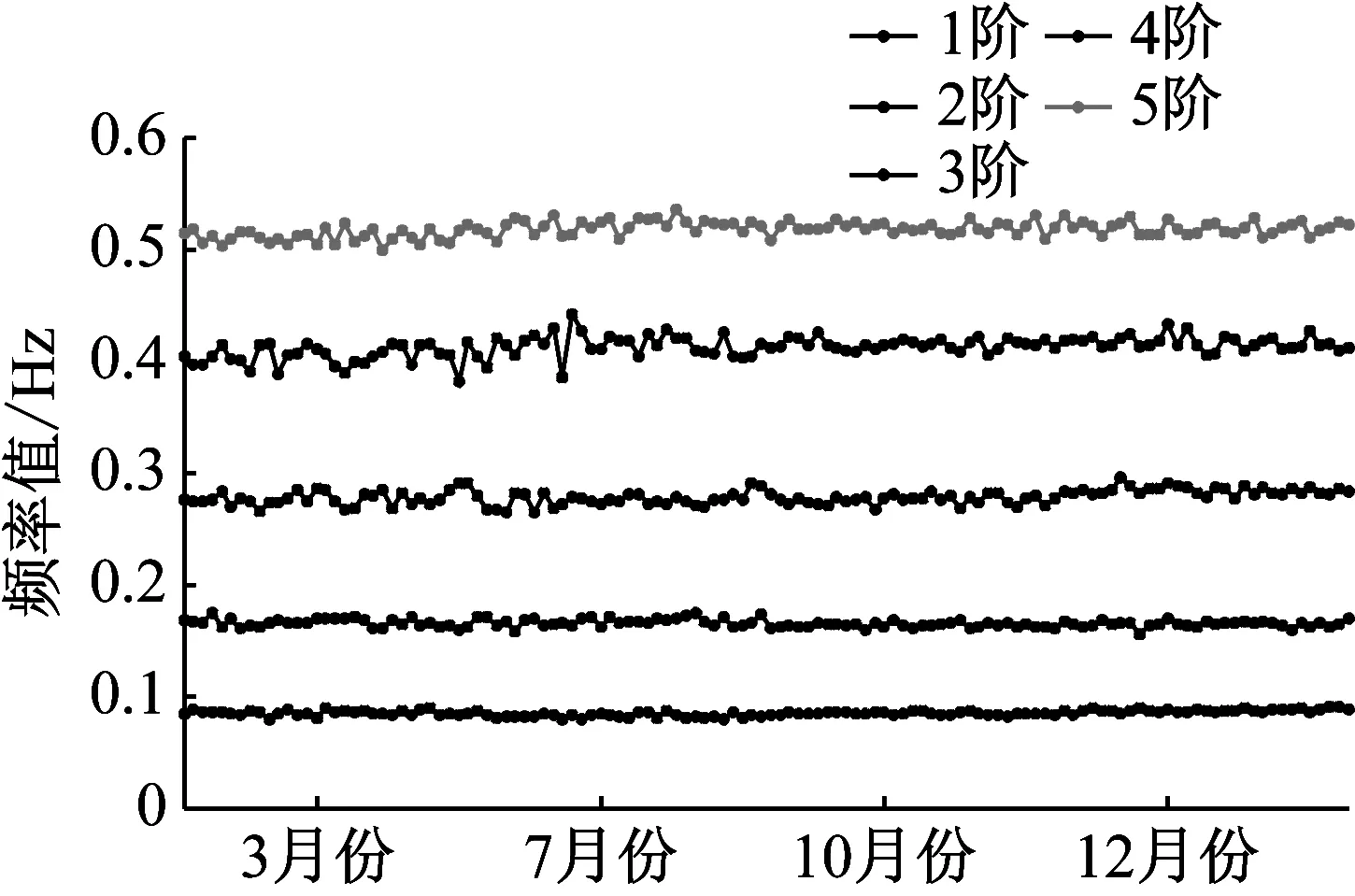
图14 横桥向前5阶频率值

4 结 论

通过将本文所提算法运用于苏通大桥的实测数据，可得如下结论：

(1) 在对实际桥梁结构进行模态参数识别时，可以通过对奇异熵增量取一阶导数来实现系统真实阶次的自动化确定，且该方法比稳定图定阶法更高效。

(2) 将谱系聚类分析法引入随机子空间算法中，能有效筛选出稳定图中的真实模态，实现模态参数的自动化识别，避免人为参与识别的主观性，提高参数识别的效率。

(3) 将“滑窗技术”引入到模态参数识别中，不仅能提高Data-SSI识别时变结构模态参数的准确性，还能对桥梁结构的动力特性进行实时监控。

(4) 将统计学中的谱系聚类算法与Data-SSI以及“滑窗技术”相结合，不仅能够实现模态参数的自动化识别，还能实现对桥梁结构动力特性的实时监控。

[1] 秦世强.桥梁健康监测与工作模态分析的理论和应用及系统实现[D].成都:西南交通大学,2013:100-120.

[2] BOONYAPINYO V, JANESUPASAEREE T. Data-driven stochastic subspace identification of flutter derivatives of bridge decks[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(12): 784-799.

[3] 淳庆,邱洪义.基于环境激励下钢桁架桥的模态参数识别[J].特种结构,2005:62-65.

CHUN Qing, QIU Hongyi. The modal parameter identification of steel truss bridge based on the environment excitation[J]. Special Structures, 2005: 62-65.

[4] 傅志方,华宏星.模态分析理论与应用[M].上海:上海交通大学出版社,2000:70-75.

[5] 刘宗政,陈恳.基于环境激励的桥梁模态参数识别[J].振动、测试与诊断,2010,30(3):300-303.

LIU Zongzheng, CHEN Ken. Bridge modal parameters identification based on environment excitation[J]. Journal of Vibration Measurement & Diagnosis, 2010, 30(3): 300-303.

[6] 孙国富.基于模糊聚类的模态参数自动识别[J].振动与冲击, 2010, 29(9): 86-88.

SUN Guofu. Automatic identification of modal parameters based on the fuzzy clustering analysis[J]. Journal of Vibration and Shock, 2010, 29(9): 86-88.

[7] 续秀忠,华宏星,陈兆能.基于环境激励的模态参数辨识方法综述[J]. 振动与冲击, 2002, 21(3): 1-5.

XU Xiuzhong, HUA Hongxing, CHEN Zhaoneng. A survey of modal parameter identification based on the environment excitation[J]. Journal of Vibration and Shock, 2002, 21(3): 1-5.

[8] 练继建,李火坤,张建伟.基于奇异熵定阶降噪的水工结构振动模态ERA识别方法[J].中国科学: E辑, 2008, 38(9): 1398-1413.

LIAN Jijian, LI Huokun, ZHANG Jianwei. Hydraulic structure vibration modal ERA identification according to de-noising order of singular entropy[J]. Science China: Series E, 2008, 38(9): 1398-1413.

[9] 章伟宜.随机子空间方法结构模态识别的数值仿真[J].工程与建设,2011,25(2): 162-163.

ZHANG Weiyi. Numerical simulation of structural modal identification in stochastic subspace identification method[J]. Journal of Engineering and Construction, 2011, 25(2): 162-163.

[10] 周思达,周小陈,刘莉,等.基于模糊聚类的模态参数全因素自动验证方法[J].北京航空航天大学学报,2015,41(5):811-816.

ZHOU Sida, ZHOU Xiaochen, LIU Li, et al. The modal parameters of the automatic verification method based on the fuzzy clustering factors[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(5): 811-816.

[11] 单德山,李乔,黄珍.桥梁动力测试信号的自适应分解与重构[J].振动与冲击,2015,34(3):1-6.

SHAN Deshan,LI Qiao,HUANG Zhen.Adaptive bridges dynamic test signal decomposition and reconstruction[J]. Vibration and Shock, 2015,34(3):1-6.

Automatic identification of Bridge structural modal parameters based on improved EEMD and hierarchical clustering algorithm

XU Jian1, ZHOU Zhixiang1, TANG Liang1, RAN Jie2, HE Jie3

(1. School of Civil Engineering, Chongqing Jiaotong University, Chongqing 404100, China;2. Nanchong Municipal Bureau of Housing and Urban Rural Developmen, 637000, China;3. School of Civil Engineering, Southwest Jiao Tong University, 610031, China)

As one important part of a bridge health monitoring system, the bridge structural modal parameters identification has a great significant meaning for a long-term health monitoring of bridges. However, the existing modal parameter identification algorithms cannot realize automatic identification of structural modal parameters and a structure system’s order. Here, a brief introduction to the basic principle of stochastic subspace algorithm was provided firstly. Then the sliding window technique was introduced to realize the on-line identification of time-varying structures’ modal parameters. Aiming at the problem that system order-determining was very difficult, the system order-determining algorithm was proposed based on the singular entropy theory to realize a system’s order automatic determining. Furthermore, the hierarchical clustering algorithm in statistics was combined with the random subspace algorithm to realize automation identification of bridge structural modal parameters. At last, the proposed algorithm was used to identify modal parameters of Sutong bridge in vertical and transverse directions. The identification results were compared with those of theoretical calculation. The results showed that this proposed algorithm can not only realize automatically determining a system’s order, but also realize automatically identifying bridge structural modal parameters to monitor bridge structural parameters in real time and understand the running status of a bridge structure.

bridge structure; sliding window technique; stochastic subspace identification; modal parameter; hierarchical clustering algorithm

国家自然科学基金(11627802;51478071)

2016-05-19 修改稿收到日期：2016-09-05

徐健 男，博士生，1987年生

周志祥 男，博士,教授,1958年生 E-mail：2252666725@qq.com

U446.3

A

10.13465/j.cnki.jvs.2017.11.033