高超声速飞行器非连续点火助推增程弹道设计*
鲜 勇,郭玮林,张大巧,雷 刚,李少朋
(火箭军工程大学,西安 710025)
高超声速飞行器非连续点火助推增程弹道设计*
鲜 勇,郭玮林,张大巧,雷 刚,李少朋
(火箭军工程大学,西安 710025)
针对高超声速飞行器因防热烧蚀而制约整体射程的问题,创新提出了一种非连续点火助推方案,通过增大助推段射程的弹道设计方法提高飞行器整体射程能力,减轻后续段的射程压力。综合考虑动压、过载、控制和终端高度、速度、弹道倾角等约束条件,以助推段射程最大为目标函数,设计了非连续点火助推段飞行程序和纵向平面弹道优化模型,采用改进的梯度粒子群算法进行优化求解。仿真结果表明,改进的梯度粒子群算法能有效解决非连续点火助推弹道设计问题,设计的非连续点火助推弹道方案在满足各项约束的同时,助推段射程比连续点火方案提高了8.7倍,射程达到了4 800 km,增程的效果十分明显。
非连续点火;助推段射程;改进的梯度粒子群算法;弹道优化
0 引言
高超声速飞行器在飞行过程中速度可达Ma=6以上,弹体需承受巨大的热烧蚀作用,远距离的高超声速飞行对飞行体结构材料要求极为苛刻,制约了远程高超声速飞行器的发展。通过增大助推段的射程,在不减小飞行器整体射程的情况下,缩小滑翔段距离,从而降低远程高超声速飞行器对结构材料的要求,将具有十分重大的意义。同时增大助推段飞行距离也可在不降低最大射程的条件下,用于提高滑翔机动能力,对提高高超声速飞行器的突防能力以应对未来可能的拦截系统同样具有极其重要的意义。国内外对高超声速飞行器助推段弹道设计问题开展了广泛的研究,但主要研究的是如何设计助推段使终端参数满足约束要求,如文献[1]基于直接打靶法和序列二次规划方法设计的助推段优化方案使得终端状态均满足约束要求,但并没有将射程作为优化指标;或者是将高超声速飞行器射程作为优化指标,但没有对滑翔入轨点参数进行约束,如文献[2]利用伪谱法对主动段和滑翔段进行优化,分析了主动段性能指标对飞行器最大射程的影响,文献[3]应用序列二次规划法求解助推高超声速飞行器最大射程,以助推段关机点最大能量(势能和动能之和)作为性能指标,这些均没有考虑助推段终端的速度约束。并且当前的公开文献中针对飞行器助推段的非连续点火弹道研究相对较少,且主要运用在地空导弹和空空导弹[4-6],所以进一步开展对非连续点火弹道的研究,特别是对高超声速飞行器的非连续点火助推弹道方案的研究意义重大[7]。
为了增大高超声速飞行器的助推段射程,本文提出一种基于一定终端约束条件下通过非连续点火增大助推段射程的弹道设计方法。综合考虑动压、过载和滑翔入轨点高度、速度、弹道倾角等约束条件,将飞行程序角、二级发动机开关机时间等控制变量作为优化参数,以助推段射程最大为目标函数,建立纵向平面内弹道优化模型。由于非连续助推弹道待优化参数和约束条件相对较多,传统的优化算法[8]解决这类复杂弹道优化问题效果并不理想,所以本文采用改进的梯度粒子群算法进行优化求解,仿真表明该算法收敛速度较快,结果既满足滑翔入轨点的速度、高度、弹道倾角条件,相比较连续点火弹道方案又明显增大了助推段射程。
1 非连续点火弹道方案设计
以二级助推火箭的高超声速飞行器为研究对象,并认为二级火箭发动机可实现多次点火。通过利用二级发动机的三次点火设计,在满足助推段过载、转弯角速率等各项约束和高超声速飞行器滑翔入轨点条件的同时,增大助推段射程。为方便讨论,本文将助推段划分为一级助推段、二级助推I段、无动力滑行I段、二级助推Ⅱ段、无动力滑行Ⅱ、二级助推Ⅲ段。高超声速飞行器非连续点火助推段弹道曲线如图1所示。
1.1 运动学模型
飞行器在发射坐标系飞行过程中受到推力、重力和空气动力、柯氏惯性力和牵连惯性力作用,不考虑横向运动时的纵向平面运动方程:
(1)
1.2 飞行程序角模型
一般情况下,火箭在亚音速段只进行一次程序转弯即可达到要求,但对于高超声速飞行器助推段来说,其主动段关机点高度相对较低,若不采用大攻角转弯就无法达到终端约束要求,而大攻角转弯会造成较大的过载,不仅使得结构和其他元件受力过大,且对控制系统要求较高,需提供较大控制力。所以,在一级的飞行阶段通过设计两次攻角转弯,用较小的攻角满足火箭飞行约束条件。
一级飞行在稠密的大气层中,应避免跨音速段有攻角转弯,所以飞行程序角设定为在速度达到Ma=0.7前进行一次攻角转弯,速度达到Ma=1之后进行二次攻角转弯,在跨音速段要求攻角为0,进行重力转弯。飞行程序设计如下:
(2)
(3)
其中,0~t1为垂直飞行段;t1~t2为跨音速飞行前的程序转弯段;t2~t3为跨音速飞行段,攻角为零;t3~t4为跨音速飞行后进行的第二次程序转弯段;t4~tk1为一二级分离前的等程序飞行段;θ为弹道倾角;α1(t)、α2(t)为飞行攻角;ωz为地球自转角速度分量;aa1、aa2为可调整的常数,am1、am2为最大攻角的绝对值,这4个变量作为控制转弯快慢的优化参数。
一级飞行结束后,飞行器飞行高度一般小于80 km,为降低二级姿态控制难度,采用二级继续工作,待飞行高度超过大气层后,再实施第二次和第三次点火的设计方案。从二级第一次点火至第一次关机的飞行段称为二级助推I段,第二次点火至第二次关机称为二级助推II段,二级第三次点火至最终关机称为二级助推III段。二级各段飞行程序采用分段线性化方法进行设计,具体形式如下:
(4)
1.3 优化模型和约束条件
(1)约束条件
非连续点火助推弹道设计的约束条件包括路径约束、控制约束、终端约束等。
路径约束又包括动压约束、法向过载约束和高度约束,动压约束、法向过载约束形式如下:
(5)
式中ρ、V分别为大气密度、合速度的标量值;q和ny分别为动压和法向过载;qmax和nmax为最大动压值和最大法向过载,qmax=60 kPa,nmax=1.5g。
(6)
控制约束主要有飞行攻角约束和程序角速率约束,形式如下:
(7)
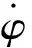
终端约束包括终端高度、终端速度和终端弹道倾角约束,形式如下:
(8)
(2)优化变量
非连续点火助推段弹道优化设计变量为
(9)
式中Tu为二级主发动机工作结束后游动发动机工作的时间;tw1、ts2、tw2、ts3分别为二级助推I段发动机工作时间、二级助推Ⅱ段发动机开机时间、二级助推Ⅱ段发动机工作时间、二级助推Ⅲ段发动机开机时间。
(3)目标函数
本文研究通过二级非连续点火助推增大射程的优化问题,因此将助推段射程Ld最大作为目标函数,即
J(X)=min{-Ld}
(10)
2 改进粒子群算法的非连续点火弹道设计
粒子群算法是一种基于群体智能的优化方法[9],采用的是速度-位移模式,每个粒子的位置对应一个解,而解的目标函数值作为判定粒子位置优劣的准则。粒子群算法由于具有收敛速度快、易于实现的特点,所以在飞行器优化领域得到了广泛的应用[10-13]。本文设计的非连续点火弹道设计优化的变量多达11个,组成的位置变量X即对应一个粒子,每一个粒子都需要计算适应度也就需要解算弹道,而弹道的解算时间相对较长,传统粒子群算法[14-15]的收敛速度慢,已不能很好地满足要求。为此,对粒子群算法进行改进,利用梯度搜索具有高效性的特点,将梯度搜索的思想应用于粒子群算法中,且对惯性权重和学习因子也进行相应的改进以加快收敛速度。
改进的粒子群算法计算流程如图2所示。具体步骤如下:
(1)种群的初始化
设定初始参数,包括以一定范围随机产生粒子的初始位置x0和初始速度v0,给出最大迭代次数kmax,最大速度vmax和种群大小NP。将每个粒子的位置记录为初始个体最优值,计算出每个粒子的适应度,比较大小找出具有最优适应度的粒子,把该粒子的位置记录为全局最优值。
(2)生成新一代种群并更新粒子的个体最优值和种群的全局最优值
a. 生成新一代种群
更新粒子群的位置和速度,计算公式如下:
(11)
为了使粒子群在飞行初期具有较好的探索能力而在飞行后期具有较好的开发能力,所以惯性权重ω采用线性递减动态调节的方法,即
(12)
为了使粒子群在飞行初期具有较大自我学习能力加强全局搜索,在飞行后期又具有较大的社会学习能力加快收敛速度,所以学习因子c1、c2采用异步变化学习因子,即
(13)
为保证优化参数满足范围,必须对位置和速度向量进行一定的约束防止超限,即
(14)
若粒子的位置和速度向量不在可行区域内,则赋以相应的边界值。
b. 更新粒子的个体最优值
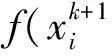
c. 更新种群的全局最优值

(3)利用梯度法再次更新全局最优值
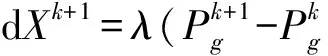
(4)终止条件判定
若k>kmax或优化结果达到给定精度,则退出计算,输出最优解;否则,返回步骤(2)。
3 仿真计算与结果分析
以某二级运载火箭为例,各级发动机参数如表1所示。利用以上改进的梯度粒子群算法分别对连续点火和非连续点火弹道方案进行优化仿真。粒子群算法种群规模NP取40,进化代数kmax取80,惯性权重最大值ωmax取0.9,最小值ωmin取0.4,学习因子c1的初始值为2.5,终止值为0.5,学习因子c2的初始值为0.5,终止值为2.5,系数λ取值为1。

表1 发动机性能参数
改进梯度粒子群算法对连续点火和非连续点火弹道方案优化的具体参数结果如表2所示(表2优化参数TT1、TT2分别为连续点火弹道方案飞行器二级段第一次、第二次等斜率转弯时间),终端关机点的参数结果如表3所示。
标准粒子群算法和改进梯度粒子群算法对非连续点火弹道方案优化的适应度收敛曲线如图3所示。
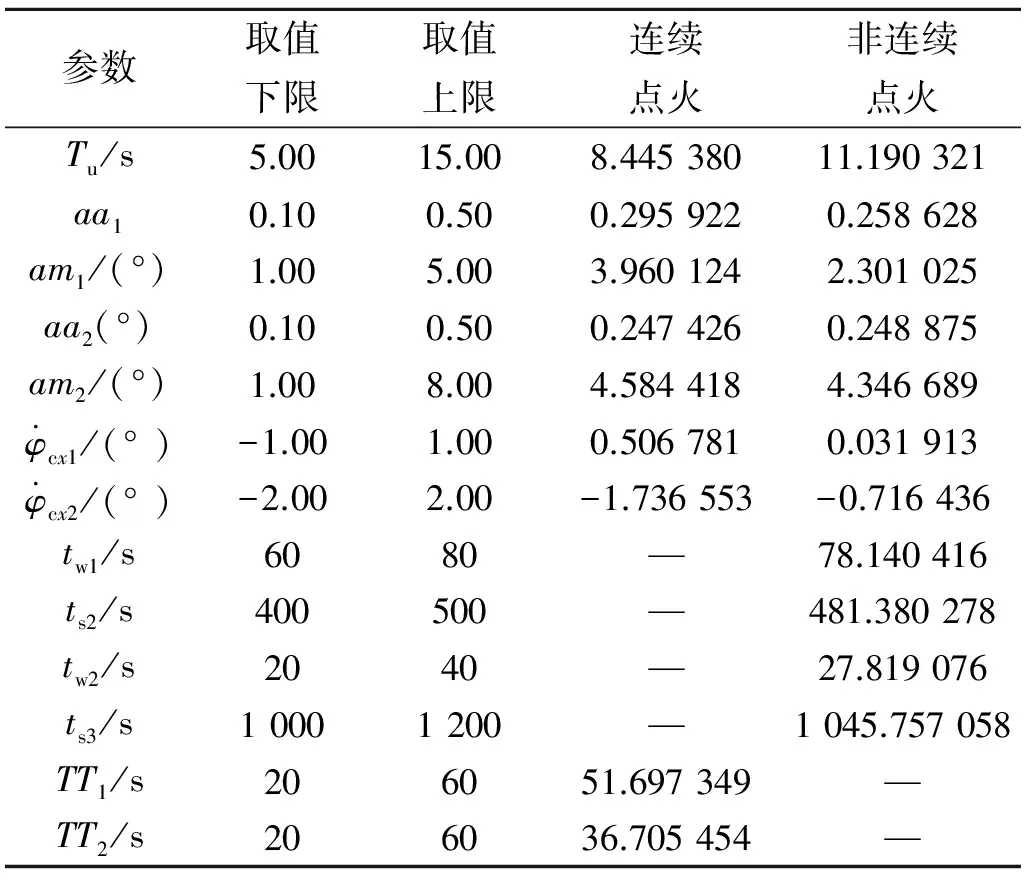
表2 设计变量优化结果

表3 终端参数结果
由图3可知,当改进梯度粒子群算法种群迭代次数为30次左右时,即得到了有效解,且其收敛速度和
收敛精度均要优于标准粒子群算法。
改进梯度粒子群算法对非连续点火弹道方案优化仿真结果具体如下:火箭飞行程序控制量随时间变化的曲线如图4所示;飞行过程中射程、高度、速度、弹道倾角、动压、法向过载和攻角等弹道参数随时间变化曲线如图5所示。

由表2和图5(a)的仿真结果可看出,基于非连续点火的助推段射程达到4 865.594 km,相比于连续点火助推段558.692 km的射程,增程的效果十分明显,同时终端高度、速度和弹道倾角也均满足约束条件。
由图5(b)~(d)可知,非连续点火助推弹道方案的终端高度、终端速度和终端弹道倾角约束满足较好,由图5(e)、(f)可知,动压、法向过载均满足约束要求。飞行器在35~46 s左右达到跨音速飞行状态,由图5(g)可知,此时攻角已为0°,有效避免了攻角转弯。
4 结论
(1)利用改进的梯度粒子群算法,有效解决了11个设计变量、8个约束条件的非连续点火高超声速飞行器助推段弹道增程的问题,且无论是收敛速度还是收敛精度均优于标准粒子群算法。
(2)本文设计的飞行程序满足弹道约束条件,攻角曲线平滑,设计的最大攻角和程序角速率均较小,利于控制系统的稳定工作;且其动压和法向过载值均保持在较小的范围有利于结构设计。
(3)在满足终端约束条件的前提下,通过多次点火的二级助推设计,确实增大了主动段的射程,并且效果十分明显,主动段射程达到4 000 km以上,比连续点火的弹道方案提高了8.7倍。因此,基于非连续点火的助推段优化设计方案在提高高超声速飞行器射程方面具有明显优势。
[1] 任京涛.助推滑翔导弹上升段多终端约束弹道设计及制导方法研究[D].哈尔滨:哈尔滨工业大学,2013.
[2] 李柯,聂万胜,冯必鸣.助推-滑翔飞行器弹道分段优化研究[J].指挥控制与仿真,2012,34(5):21-25.
[3] 李瑜,杨志红,崔乃刚.助推-滑翔导弹弹道优化研究[J].宇航学报,2008,29(1):66-70.
[4] 张弫,郑时镜,于本水.遗传算法在远程防空导弹总体优化设计中的应用[J].系统工程与电子技术,2003,25(1):34-37.
[5] 王志健,何国强,魏祥庚,等.空空导弹多脉冲固体火箭发动机能量分配优化研究[J].弹箭与制导学报,2010,30(6):144-146.
[6] Carrier J L C.Dual-interrupted-thrust pulse motor[J].Journal of Propulsion and Power,1987,3(4):308-312.
[7] 程仙垒,彭双春,郑伟,等.多约束条件下非连续助推弹道方案设计与优化[J].系统工程与电子技术,2015,37(4):0888-0894.
[8] 杨希祥,李晓斌,肖飞,等.智能优化算法及其在飞行器优化设计领域的应用综述[J].宇航学报,2009,30(6):2051-2061.
[9] Kennedy J,Eberhart R.Particle swarm optimization[C] // Proc.of the IEEE International Conference on Neural Networks,1995:1942-1948.
[10] Pontani M,Ghosh P,Conway B A.Particle swarm optimization of multiple-burn rendezvous trajectories[J].Journal of Guidance,Control,and Dynamics,2012,35(4):1192-1207.
[11] Ran M P,Wang Q.Spacecraft rendezvous trajectory optimization method based on EPSO[J].Journal of Astronautics,2013,34(9):1195-1201.
[12] Pontani M,Conway B A.Optimal finite-thrust rendezvous trajectories found via particle swarm algorithm[J].Journal of Spacecraft and Rockets,2014,94(1):434-445.
[13] Duan H B,Yu X Y,Parameters identification of UCAV flight control system based on predator-prey particle swarm optimization[J].Science China Information Science,2013,56(1):1-12.
[14] 杨希祥,江振宇,张为华.基于粒子群算法的固体运载火箭上升段弹道优化设计研究[J].宇航学报,2010,31(5):1304-1309.
[15] Pontani M,Conway B A.Particle swarm optimization applied to space trajectories [J].Journal of Guidance,Control,and Dynamics,2010,33(5):1429-1441.
(编辑:吕耀辉)
Trajectory design of improving range for hypersonic vehicle based on discontinuous booster
XIAN Yong,GUO Wei-lin,ZHANG Da-qiao,LEI Gang,LI Shao-peng
(Rocket Force University of Engineering,Xi’an 710025,China)
A novel discontinuous ignition booster method has been proposed in the present work to solve the restriction issues of the whole range,which are caused by the thermal ablation of the hypersonic vehicles.The controlling stress of the gliding range has been alleviated via an increase of the boost phase range.Setting the multi-parameters,such as dynamic pressure,overloads, controlling and terminal height,speed,and trajectory angles as the constraint conditions, and regarding the maximum distance of boost phase as the objective function,the flight program designs of the vehicles, as well as the optimization model of vertical plane trajectory have been established. Comparisons of the simulated results with the experimental ones demonstrated that the improved grads particle swarm optimization algorithm(IGPSO)can be efficiently applied to solve the discontinuous booster trajectory project with all the constraint conditions fulfilled,and the boost phase range of the discontinuous booster case has been improved by 8.7 times compared to that of the continuous with a range of 4 800 km.The results demonstrated a conspicuous improving effect.
discontinuous booster;the boost phase range;the improved grads particle swarm optimization algorithm;trajectory optimization
2015-11-24;
2015-12-25。
鲜勇(1972—),男,教授,研究方向为飞行器设计、制导理论等。E-mail:xy603xy@sohu.com
V412.1
A
1006-2793(2017)03-0397-06
10.7673/j.issn.1006-2793.2017.03.022

