诗歌与数学

吴朝阳，数学博士，历史学博士，计算机科学硕士，目前任教于南京大学。

在没有书写传统的时代，要将重要的文本没有差错地传给后人是相当困难的。而由于诗歌有固定的格律，文词的改变会因其破坏原有格律而被察觉，所以，将文本编成诗歌的形式有助于在传承过程中杜绝错误，人类最早的文学作品在形式上都是诗歌，正是由于这个原因。古印度文献现存最古老的四大《吠陀》，其诗句数以万计，但它们依靠其文本的格律特征口耳相传，2000多年来没有走样地流传到现在，可见诗歌格律在印度文化中的重要性。

古印欧语系的希腊语、拉丁语和梵语都是“长音

音节型”语言，也就是说，它们以发音的长短区分音节是否被强调。因此，其诗歌格律的特征是以每行诗句中长短音节序列的构成来刻画的。这个特征使梵语得以拥有巨量的诗歌格律，古印度学者于是提出了关于诗歌格律理论上可能达到的数目及其分类的问题，而对这些问题考虑得很早而且深入的古印度学者是宾伽罗。

宾伽罗是一位公元前4世纪左右佛教重要的“中观论”学者，但他所著的《檀陀经》重点讨论的却是关于诗歌格律的数学问题。宾伽罗不仅对描述现实存在的格律感兴趣，而且想要研究所有理论上可能存在的格律，于是他提出问题：我们能够想出多少种不同的格律？我们又如何用系统性的方法找出那些目前的诗歌中还没有出现的格律？

宾伽罗的思考代表着数学思维的根基之一，他的研究是组合数学的源头。现在全世界的中学和高等院校都在讲授组合数学知识，然而其源头出自诗歌这一事实，却长期被人们所忽略。

梵语音节分长音节和短音节2种，一个长音节所占用的时问长度大约是短音节的2倍。在语言学中，衡量音节时间长度的单位称为“音拍”，代表1个短音节所占用的时间。因此，1个短音节时长为1音拍，而1个长音节则是2个音拍。当然，由于人们的语速彼此相异，音拍只是相对的概念，不是一个可以用秒计量的物理时间单位。

音拍的概念确立之后，梵语诗句的格律可以这样定义：

一种长音节与短音节的序列模式就是一种（诗句的）格律。

我们用“”表示1个长音节，而用“～”表示1个短音节，则我们可以将格律表示成图形。例如，“～～-～-～-～-”是包含有5短、5长，10个短长音节相间的一种格律，时长总共是15个音拍，称为“五音步抑扬格”。另一种出自古印度的格律名为“曼妙女郎”，它的格律形式为：“～～～～-～～-～-～”，它包含有8短、4长，总共16个音拍，它的名称来自用该格律所写的一首诗——一首年轻人在与恋人共度良宵之后问候恋人的诗歌。

宾伽罗的《檀陀经》考虑很多不同情形下诗歌格律总数的问题，其中一种是每行诗句的时长都相同的情形。也就是说，对某个自然数n，考虑时长同样为n个音拍的诗行，计算具有n个音拍的诗句格律的数目——这就是“宾伽罗第一问题”：

总时长为n个音拍的格律总共有多少种？

这其实是计算一个特定集合的元素个数的问题。具体来说，这个集合的元素是理论上可能的格律，即长音节与短音节排成的序列，而每个这种序列的总音拍数是事先给定的自然数n。

数学研究的第一步通常是给研究对象命名。这里我们感兴趣的对象是总时长为n个音拍的格律的总数，为方便讨论，我们将“总时长为刀个音拍的格律总数”命名为A（n）。

对数学家而言，n确实是任意的自然数。为了讨论的完整性，数学家也会考虑n=1及n=2这种与诗歌格律基本不相关的情形。然而，这些情形的答案是很容易得到。当=1时，唯一的可能是全句为1个短音节，因此A（1）=1。相似地，n=2时，诗句只能是2个短音节或1个长音节，因而A（2）=2，也就是说我们有：A（1）=1，A（2）=2。

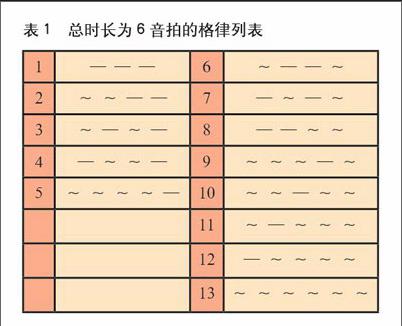
现在，我们可以开始系统性地探讨，尝试着计算对n=3，4，5，6等情形A（n）的数目。例如，如果n=6，我们可以找出如下13种不同的格律。

我們很快会觉得这样的列表实际上似乎没有什么意义，对比较大的刀，可能的格律形式增长得太多，根本难以列举——那时怎么才能知道我们的列表有没有遗漏？因此，对任意的刀，另找出路才是确定A（）的聪明想法。数学家在攻克问题时有时会采用反向推导的办法，下面我们就采用这种策略解决求解A（n）的问题。

如果观察表1中的2组格律，也许有人会找到解决问题的思路。表中的第1组有5个格律，而第2组则有8个。这2组之间的区别在哪里？答案是：它们结束处的音节不同。第1组都是以长音节结束的格律，而第2组则全部都以短音节收尾。我们先来考察第1组：除去结束处的长音节，它们剩余部分的时长全部都等于4个音拍，可见，这一组其实就是所有的4音拍格律在最后添加1个长音节。因此，第1组格律的总数等于A（4）。相似地，第2组就是所有的5音拍格律在末尾添加1个短音节而得到的格律，因此第2组的数目等于A（5）。这样，我们就得到一个关于A（6）的公式A（4）+A（5）=A（6）。

很显然，对任何自然数刀，我们都可以进行类似的推导。对任何一种总时长为刀音拍的格律而言，它要么以长音节结束，要么以短音节结束。因此，时长为刀的格律之集合可以分成2组，一组以长音节结束，另一组以短音节结束。以短音节结束的格律可以以任意一种时长为n-1的格律开头，因而这组格律的总数目等于A（n-1）。相似地，以长音节结束的格律的总数等于A（n-2）。因此，我们总结出如下公式：A（n-2）+A（n-1）=A（n）。

这个公式当n-2至少等于1的时候一定成立，或者说，它对所有n≥3都是正确的。这样，我们汇总已有的结果，得到：A（1）=1，A（2）=2；A（n-2）+A（n-1）=A（n），对所有大干2的自然数n成立。

我们承认，上述公式并没有直接告诉我们A（n）等于多少，但在某种意义上说，它已经解决了宾伽罗第一问题。这个公式描述了从关于A（1）和A（2）的“初始条件”出发，逐步计算A（n）的办法：

A（3）=A（1）+A（2）=1+2=3，A（4）=A（2）+A（3）=2+3=5，

A（5）=3+5=8，A（6）=5+8=13，A（7）=8+13=21，如此等等。

总之，每一个A（n）都是它前面2个的和，而我们现在可以肯定表1中没有任何遗漏，因为上述计算结果证实：A（6）确实等于13。

只要略微有点耐心，我们不难计算出A（16）=1597，从而得到总时长为16个音拍的格律的总数。前文提到的“曼妙女郎”这种古老的印度格律，只是所有理论上可能的1 597种16音拍格律中的1种。

作为宾伽罗第一问题的答案，A（n）在公元前就以晦涩的语言描述出现在《檀陀经》中。在西方，1，2，3，5，8，13，21，34…，这个后一项等于前两项之和的数列多次被重复发现，由于不知道印度人早在1 000多年前就发现了这个数列，法国数学家爱德华·卢卡斯（1842-1891）将这个数列称为斐波那契数列。

在某个情形的思考可能被应用于几乎毫不相关的另一情形，这是数学一个引人入胜的方面。上述的格律计数问题就在许多其他情况下出现，我们下面举2个例子。

（1）花園小路问题。假设我们要给花园小路铺上长方形砖块（如图1所示），砖块的方向既可以与小路相同（以下称“横向”），也可以与小路的方向相垂直（以下称“竖向”）。那么问题来了：用16块砖可以铺出多少种不同的样式呢？

这个问题与上述宾伽罗第一问题是很相似的。1块竖向的砖可以对应于1个短音节，而2块横向的砖则构成1个对应着1个长音节的单元。长音节的时长是短音节的2倍，而1个横向单元则总共有2块砖。小路由单块竖向砖与双块横向单元的序列所构成，而格律由单音拍的短音节与双音拍的长音节排列而成，二者恰可类比。因此，由这种相似性我们可以得到这样的结论：16块砖横铺和竖铺，总共可以铺成的A（16）种，即1 597种不同花样的花园小路。

（2）邮差登楼问题。邮递员每天需要登上同一个共有16个梯级的楼梯去投递邮包。他上楼时有时1步只上1个梯级，有时则1步跨上2个。为了让工作有些趣味，他决定每天用1种不同的单梯级与双梯级序列上这个楼梯。他的问题是：不同的单梯级与双梯级的序列总共有多少种？

略加思考我们就会发现，这个问题与宾伽罗第一问题相似，与花园小路问题同样也相似，因此，3个问题的答案是一样的，即A（16）=1597。