农用无人机群体作业下的一致性控制

邵俊倩

（绥化学院信息工程学院 黑龙江绥化 152061）

农用无人机群体作业下的一致性控制

邵俊倩

（绥化学院信息工程学院 黑龙江绥化 152061）

对有leader的农用无人机群体作业下的一致性控制问题进行研究。针对农用无人机间通信时滞和农用无人机与leader间时滞相同的情况，采用时域LMI方法得到农用无人机群体作业下达到一致性的充分条件，通过解线性矩阵不等式得到了系统的最大容时滞许值。最后，通过仿真实验验证了结论的正确性。

农用无人机；群体作业；时滞；一致性；控制

黑龙江省是中国重要的商品粮基地，是中国最大的粮仓。黑龙江省的农业代表了中国农业，引领了中国农业，因此，黑龙江农业生产存在的问题也是全国农业生产存在的问题。黑龙江省粮食生产安全问题仍然面临着严峻的挑战，主要体现在粮食质量安全、病虫害防治、农药残留超标及浪费严重，土地肥力下降等问题上。滥用农药化肥现象仍然存在，对粮食质量造成了一定危害。随着农村产业化的调整，农民对适用机械化新技术和各种配套机具的需求越来越迫切，农用无人机具有作业效率高、操作安全、速度快、性能稳定和防治范围广等优点，在农林植保喷药、风力授粉、农田遥感等方面独特的作业优势近年来受到广泛的关注，具有越来越广阔的应用前景。

一致性问题作为协调控制的基础，已广泛应用于无人飞行器联合控制、编队控制、蜂拥控制、聚集问题、同步以及协调决策等问题的研究中，其中一个研究方向是有leader的多智能体系统协调控制。关于有领航者的多智能体系统一致性问题，研究者已做了大量的工作[1-6]。农用无人机群体实际上就是一个多智能体系统，农用无人机群体作业并达到一致，能够扩大作业面，有效避免重复喷洒，保护生态环境，减少支出，降低成本，提高农用无人机群体作业的效率，有广泛的应用前景。本项目对有leader的农用无人机群体作业下的一致性控制问题进行研究，考虑农用无人机间通信时滞和农用无人机与leader间时滞相同情形下多农用无人机系统如何达到一致。

一、图论基础

有向图G(V,E,A)包含n个节点，其中V={e1,e2,…，en}为节点集，E哿V×V为图G的边集，其元素eij=(i,j)∈E称为图G的边，边的权值矩阵为A=[aij]称为邻接矩阵，其中aij叟0(i≠j)，aii=0。图G的节点在集合I={1,2,…,n}中取值。如果这个有向图满足aij=aji(i,j∈I)，则图G称为无向图。节点ei的邻集可以记为Ni={ej∈V:(ei,ej)∈E}，图G的Laplacian矩阵为L=(lij)，其中lij=。如果存在一个节点使得任意节点到这个节点都有有向路径，则称有向图是强联通的。

引理1：设L是有向图G的Laplacian矩阵，则L有一个零特征值，其余n-1个特征值全部具有正实部。特别的，若G是无向图，它的特征值全是正实数。

二、多农用无人系统模型

考虑由n+1个农用无人机e0,e1,…,en构成的多农用无人机系统，其中节点e0代表leader且为全局可达点，其它节点e1,e2…,en代表跟随者。同样，定义一个对角矩阵D∈Rn×n为leader的邻接矩阵，其对角元素为di=ai0。如果节点e0是节点的邻居节点ei，则ai0＞0；否则，ai0=0。其余n个跟随者的系统动态可描述为

假定leader的速度为恒定值，它的运动状态是独立的，不受其它节点的影响，而跟随者受leader和其它跟随者的影响。领航者的状态方程为

其中，x0(t)为leader的位置，V0为期望的常值速度。

控制协议设计的目的是使跟随者与leader的位置和速度趋于相同，即多农用无人机系统（1）达到一致当且仅当农用无人机的位置和速度变量分别满足：

为了解决上述有leader的二阶多农用无人机系统的一致性问题，在切换拓扑网络结构下，考虑农用无人机之间的通信时滞和农用无人机与leader之间通信时滞相等的情况，选取如下控制协议：

其中，k1＞0,k2＞0为控制参数，aij为有向图边的权值，τ是系统中农用无人机间的通信时滞，di为leader邻接矩阵中的元素，且di=ai0。下面仅讨论农用无人机之间的通信时滞τij和农用无人机与leader之间通信时滞τi0相等的情况，即

利用控制协议（4），第一种情况下变拓扑网络下系统动态可表示为

这里Lσ是图的Laplacian矩阵，Dσ为leader与跟随者之间的邻接矩阵，‘茚’表示Kronecker积。

三、有leader的二阶多农用无人机时滞系统稳定性分析

引理2[7]设向量x,y∈Rn，对任意正定矩阵，E∈Rn×n有

2xTyxTN-1x+yTNy.

引理3[8]（Schur补引理）对于给定对称矩阵，则S＜0当且仅当S11＜0, s22-ST22S-111S12＜0，或等价地，S22＜0,s22-ST22S-122S12＜0.

定理1 考虑农用无人机之间的通信时滞和农用无人机与leader之间通信时滞相等的有向切换拓扑网络结构下的二阶多农用无人机时滞系统，利用控制协议（4），如果存在对称矩阵P＞0,M＞0,N＞0,且P,M,N∈R2n×2n满足

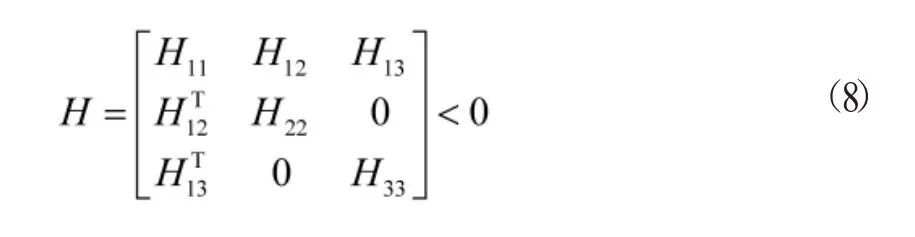
则多农用无人机时滞系统（7）能够达到一致。其中，

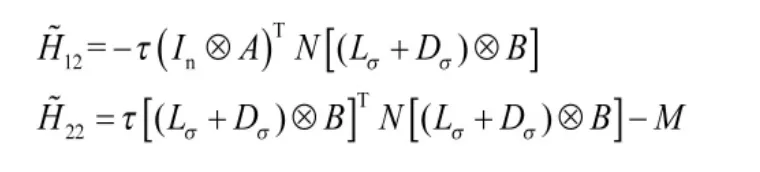
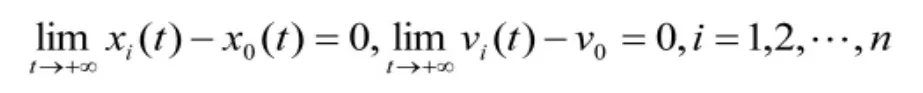
综上所述，有leader的有向切换拓扑网络结构下的二阶多农用无人机时滞系统（7）可以达到一致。

四、仿真结果

考虑包含4个农用无人机的有leader变拓扑时滞有向网络，图1中Wa,Wb,Wc表示三种不同的农用无人机与eader的连接拓扑图，每一边对应的权值为1，领航者0为全局可达点。图2为拓扑切换图，描述了切换从Wa开始每隔.01秒切换到下一个状态。设leader的初始状态及期望速度为x0=0，v0=0.2系统状态的初始值设为

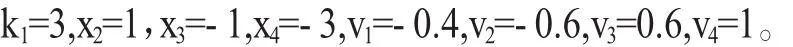
取协议参数K1=K2=1应用定理1，可知线性矩阵不等式8）有可行解，并解得系统的最大容许时滞为τ=0.469s。这里取τ=0.3s，变拓扑网络的位置和速度误差曲线分别为图3和图4，所有农用无人机与leader能够达到渐近一致。仿真结果说明定理1结论的正确性。

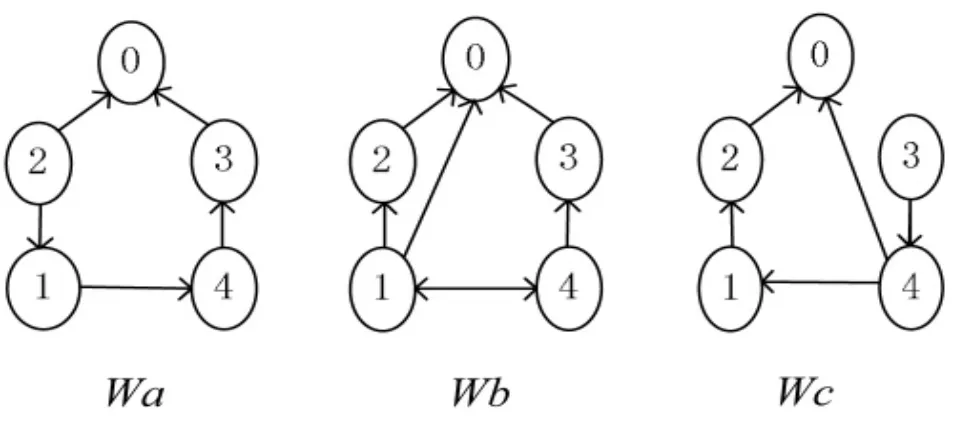
图1 农用无人机与leader的连接拓扑图

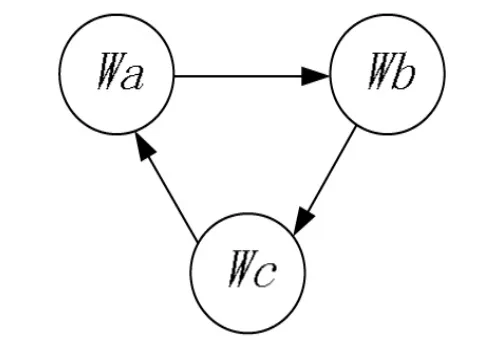
图2 拓扑切换图

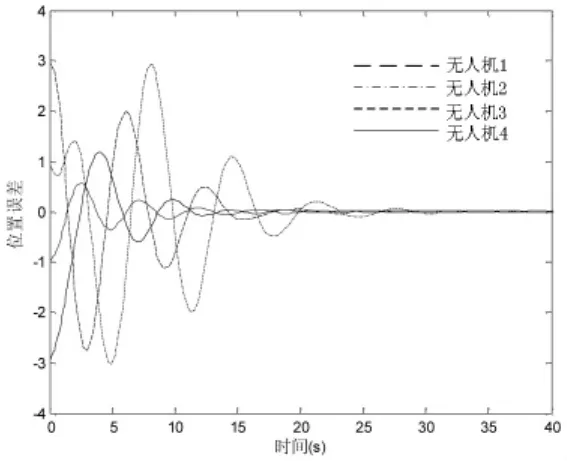
图3 τ=0.3s时位置误差曲线

图4 τ=0.3s时速度误差曲线

五、结论

本文对有leader的农用无人机群体作业下的一致性控制问题,采用时域LMI方法进行研究，考虑了农用无人机间通信时滞和农用无人机与leader间时滞相同情形下的一致性，得到了农用无人机群体作业下一致性的充分条件，通过解线性矩阵不等式得到时滞的最大容许值。下一步可研究农用无人机间通信时滞和农用无人机与leader间时滞不相同情形下的一致性控制。

[1]HU J P，HONG Y G.Leader-following coordination of multiagent systems with coulping time delays[J].Physica A：Statistical Mechanics and its Applications，2007，374(2)：853-863.

[2]Xiao F,Wang L.Asynchronous consensus in continuoustime multi-agent systems with switching topology and timevaryingdelays[J].IEEETransactionson Automatic Control,2008, 53(8):1804-1816.

[3]PENGK，YANGYP.Leader-followingconsensusproblem withavarying-velocityleaderandtime-varyingdelays[J].Physica A：Statistical Mechanics and its Applications，2009，388(2)：193-208.

[4]QIN J，GAO H J，ZHENG W X.Second-order consensus formulti-agentsystemswith switching topology and communicationdelay[J].Systems&ControlLetters，2011，60(6)：390-397.

[5]ZHANG Q，CHEN S H，YU C C.Impulsive consensus problem of second-order multi-agent systems with switching topologies[J].CommunicationsinNonlinearScienceandNumerical Simulation，2012，17(1)：9-16.

[6]RUDY C G，NEJAT O.Exact stability analysis of secondorder leaderless and leader-follower consensus protocols with rationally-independentmultiple time delays[J].Systems&Control Letters，2013，62(6)：482-495.

[7]De Souza C.E.and Li X..Delay-Dependent Robust H∞Control of Uncertain Linear State-Delayed Systems[J]. Automatica,1999,35(7)：1313-1321.

[8]贾英民.鲁棒H∞控制[M].北京：科学出版社，2007.

[责任编辑 郑丽娟]

Consensus Control of Unmanned Helicopters for Agricultural Application in Group Work

Shao Junqian
（College of information engineering,Suihua University,Suihua,Heilongjiang 152061)

The consensus control problem is studied for agricultural unmanned helicopters with one leader in group work.The time domain linear matrix inequality (LMI)method is employed when communication delay of agricultural unmanned helicopters is equal to delay between agricultural unmanned helicopters and the leader.Sufficient condition in terms of LMI is derived to ensure consensus,which can provide the allowable upper bound of time-delay.Finally a simulation example is provided to show the correctness of theoretical results.

agricultural unmanned helicopter;group work;delay;consensus;control

TP319.9

A

2095-0438（2017）06-0138-04

2017-02-18

邵俊倩(1980-)，女，黑龙江绥化人，绥化学院信息工程学院讲师，硕士，研究方向：多智能体系统协调控制。

绥化市科技计划项目（编号：SHKJ2015-017)。