合理利用“三力汇交”原理解决共点力平衡问题

江西省玉山县第一中学(334700)

陈 明●

合理利用“三力汇交”原理解决共点力平衡问题

江西省玉山县第一中学(334700)

陈 明●

高中力学中，物体受到三个力而处于平衡的问题是很常见的.物体受到三个不平行外力作用而平衡，这三个力的作用线必在同一平面上，这三个力的作用线相交于同一点，即为共点力.将这一规律称为“三力汇交”原理.

本文将结合一些例题，对例题进行分析、探讨，如何巧妙的使用“三力汇交”原理来解答平衡问题.

例题1 如图1所示，用两根轻绳把重为G的棒悬挂起来，棒恰好处于水平静止状态，一根绳与竖直方向的夹角θ=30°，另一根绳子与天花板夹角也是θ，设棒长为0.6 m，那么棒的重心到其右端的距离为多少？两根绳子的拉力分别为多少？

解析 棒在自身重力G、两绳的拉力F1、F2作用下而处于平衡状态，由于三力共面不平行，故三力作用线必交于一点，作出棒的受力分析，如图2所示，将F1、F2作用线延长交于O点，则重力作用线必过O点，且垂直于AB，过O作竖直线与AB交点即为重心C

在直角三角形AOB中有AB=0.6 m，BO=ABsin30°=0.3 m，CB=BOsin30°=0.15 m

所以，棒的重心到其右端的距离为0.15 m.

由平衡条件，可知F=G，如图3所示.

点评 棒不能看作质点，两绳的拉力、重力并不是作用于同一点，但三个力的作用线，相交于一点，这样将非共点力平衡问题转化为共点力平衡问题.

例题2 质量为m的均匀绳两端悬于同一水平天花板上的A、B两点,如图4所示，静止时绳两端的切线方向与天花板成θ角，绳的A端所受拉力F1为多少？绳中点C处的张力为F2为多少？其中c点是绳的最低点.

解析 绳受到A、B两端的拉力、自身重力，而处于平衡状态，根据对称性可知，绳的A端所受拉力与绳的B端所受拉力大小相等，对绳的一半分析(左半部分).

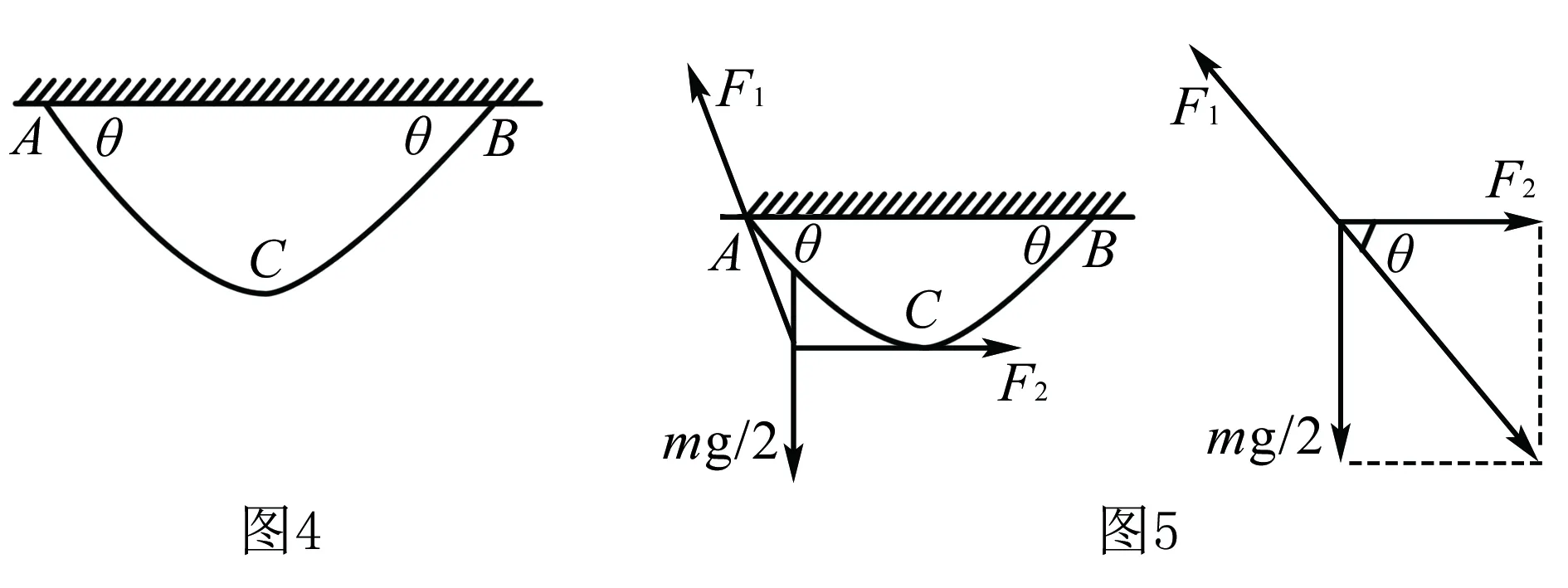
由于只对绳的一半分析，所以绳的一半重力为mg/2，绳还受到A点拉力F1，最低点右侧绳对左侧绳的拉力F2，受力分析如图5所示，由图可知，

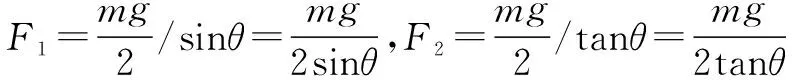
点评 由对称性可知，绳受到A、B两端的拉力大小相等，并且可将绳看作成左右两部分还有半段绳的重力，从而巧妙构建了“三力汇交”.

例题3 如图6所示，一梯(不计重力)斜靠在光滑墙壁上，今有一重为G的人从地面沿梯上爬(不考虑人的速度变化)，设地面的摩擦力足够大，人在上爬过程中，墙对梯的支持力N和地面对梯的作用力F的变化分别是____.

解析 将梯、人看作整体，整体受到墙的作用力N、地面的作用力F(地面对梯的作用力是地面对梯的弹力和摩擦力的合力)，还有人的重力(不计梯的重力).受力分析如图7所示，由图可得

N=G/tanθ，F=G/sinθ

人在上爬过程中，θ越来越大，则N、F都将由小变大.

点评 人在上爬的程中，N、F都将发生变化，但不考虑人的速度变化，是动态平衡，将人与梯看作整体，通过“三力汇交”原理，N、F的合力与重力等大反向共线，再利用矢量关系得出相应的N、F的变化规律.

例题4 一根质量为m的匀质细圆柱杆，A端通过光滑铰链固定于竖直墙上，B端系上细绳，细绳水平，另一端系于竖直墙上C点，如图8所示.已知AC=4 cm，BC=6 cm，圆柱杆A端所受的弹力F？

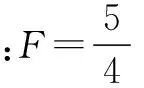
点评：圆柱杆可绕A转动，在细绳作用下，处于平衡状态.本题可利用力矩平衡来求解，但效果欠佳；但利用“三力汇交”原理明显简单很多.

例题5 重力为G的均质杆一端放在粗糙的水平面上，另一端系在一条水平绳上，杆与水平面成α角，如图10所示.已知水平绳中的张力大小为T，求地面对杆下端的作用力大小和方向.

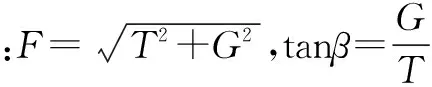
点评 杆受到地面支持力、摩擦力，还有绳的拉力，以及自身重力，共四个力，先将支持力、摩擦力合成，杆受到三个力作用，再利用“三力汇交”原理分析.对于物体受

到多个力作用时，可将其中一些力先经行合成从而构建“三力汇交”.

例题6 如图12所示，一根重8N的均匀直棒AB，A端用绳吊在固定点0，用一沿水平方向的力F=6N作用于B端，使棒处于平衡状态，则绳与竖直方向的夹角为多少？

解析 对直棒AB受力分析，受到重力mg、向右的已知力F、绳子的拉力T，由“三力汇交”原理，如图13所示，根据平衡条件，结合几何关系，有

tanθ=F/mg=6/8=0.75故θ=37°.

由于绳子的弹力沿着绳并指向绳子的收缩方向，故绳子与竖直方向的夹角为37°.

点评：根据“三力汇交”原理画出受力分析图，轻松解决问题，可见画好受力图对解题有很大的帮助.

从以上分析不难看出，这类问题中受力物体不能看作质点，基本方法是：先要画好受力分析图，再利用对称性、力的合成等方法通过分析，巧妙合理构建“三力汇交”，从而快速解答问题.

G632

B

1008-0333(2017)01-0085-02