高中物理学习中常用思维方法的运用分析

辽宁省鞍山市第二十四中学(114000)

王 影●

高中物理学习中常用思维方法的运用分析

辽宁省鞍山市第二十四中学(114000)

王 影●

高中物理一直是理科中的难点科目.要在高考中做到思路清晰，有条不紊的解题，理解一个个物理现象是远远不够的.除此之外，对不同的物理题型进行解读，并总结出不同类型的解题思维也必不可少.只有掌握这些解题思维，并加以训练，才能在高考中做到快人一步.本文对高中物理的常用方法进行了梳理，并利用实际案例来加以证明，以期在高中物理中提供一点教学经验.

高中物理；思维方法

掌握不同的物理解题思维，和提高物理成绩有着直接的关系.高中物理一般都是大部分学生的难点，通过梳理这些常用的解题思维，可以帮助学生在复习中事半功倍，提高学习效率.本文将对常用的思维方法，即临界思维、逆向思维、代换思维、估算思维法进行探讨，并加以运用到实际的习题中.为学习高中物理提供更智慧的学习方法.

一、临界思维法

临界思维也可称为极限思维，临界状态是指物体由上一个过程进入到下一个过程的过渡状态.在高中物理中一些物理概念的引入也用到了极限思维法，例如瞬时速度的引入，就是利用平均速度的概念，将时间取得很短时，平均速度就可以认为是该时刻的瞬时速度了.在力学电学等章节中也经常会出现求极值的问题.对这种类型的题目，用临界思维来解决可以达到四两拨千斤的效果，可以把解这种题目的思维称为临界思维.临界思维解题最为关键的部分就在于找出描述物体状态变化过程的物理量的临界值，根据临界值来寻找题目的突破口是解题的关键，达到根据对象物理量在临界值前后的特征进行求解.下面将举例进行说明.

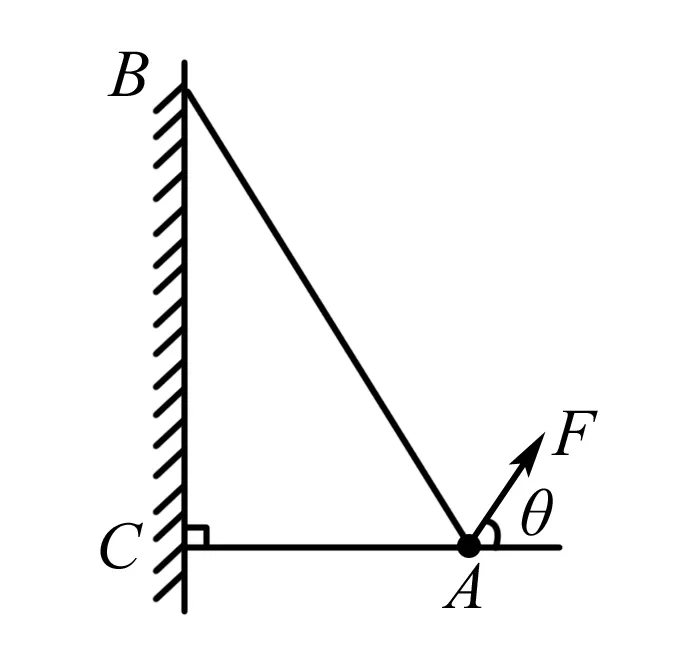
图1

例1 如图1A物体的质量重4 kg，AB和AC为两根轻绳，AB和AC的的两个端点B和C系在墙壁上，另一端点系在物体A上，(LAB=2LAC)，此外，在物体上，再施加一个外力F，且F与水平方向形成夹角θ=60°，要使两根轻绳都能伸直，求拉力F的范围.(g=10 N/kg)

解 根据题意可知要使AB、AC两根绳子拉直，即两根绳子受力FAB、FAC不能为零，所以AB、AC绳子受力各为零时为F的临界范围，求得F的范围.

(1)当FAC=0时，对球进行受力分析，如图2：

垂直方向受力平衡得出：

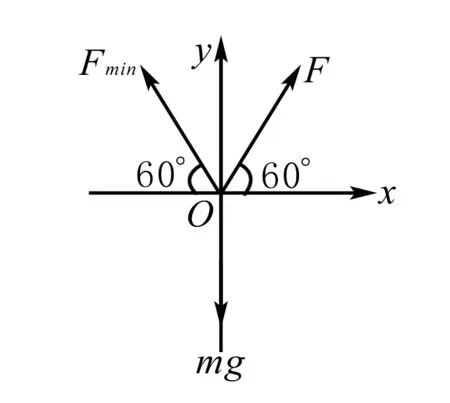
图2

(F+FAB)*sinθ=G=mg

(1)

水平方向受力平衡得出：

F*cosθ=FAB*cosθ

(2)

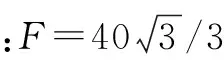
(2)同理当FAB=0时，对球进行受力分析：

垂直方向受力平衡得出：F*sinθ=mg

(3)

水平方向受力平衡得出：F*cosθ=FAC

(4)

图3

例2 如图3所示电路中，将滑片P向下移动少许，则两个理想电表的示数变化情况是( ).

A.电压表和电流表示数都减小

B.电压表和电流表示数都变大

C.电压表示数增加，电流表示数减小

D.电压表示数减小、电流表示数增大

本题中，滑片P的下滑可以外推到滑到最下端，则R3被短路，从而直接得到电流表示数为零，电压表示数减小的结论，所以选A.

综上,临界法解题的关键是找到临界点进行分析和计算.但需要注意的是所选的自变量(物理量)从某一数值变化到临界点的过程中，因变量的变化是单调递增或单调递减的情况才可以应用此法.

二、逆向思维法

逆向思维也称反演法，与正向思维比较起来，物理学的发展过程中，一些科学家就是运用逆向思维提出新课题从而推动物理学的发展进程的，比如在1831年奥斯特发现电流的磁效应现象后许多物理学家就考虑到这种现象的逆过程是否存在，就是：既然“电”能“生”磁 ，那“磁”也应该能“生”电，几乎在同时代就有许多科学家投入到由磁生电的科学研究中，最终法拉第用了十年时间找到了用磁生电的方法，使人类社会大量使用电能成为可能.才有了后来的电气化时代到来的可能.再比如麦克斯韦在总结法拉第的变化的磁场能产生电场这一规律时，也用到了逆向思维法，他受此启发，提出了猜想：既然变化的磁场能产生电场，那么变化的电场也能产生磁场，在这个了不起的猜测之后，麦克斯韦将两种情况进行汇总，预言了电磁波的存在.在麦克斯韦离世后不久赫兹在实验里逮住了电磁波，证实了电磁波的确存在，为人类社会进入信息化时代做好了铺垫.那么，在高中物理学习中适当运用逆向思维也可以使相关题目的解决事半功倍.通过对物理题目进行分析，运用逆向思维也是解决问题的一种良好的手段.很多试题都要从所求的结果反推到已知条件之后才能从已知条件入手一步一步得到最终答案.没有经过长期的逆向思维训练，在初期会感觉到一定难度，但熟练运用后，会愈加得心应手.例如匀减速运动的题型用正向思维来解题一般步骤繁多，经常也会发生无法求解的状态.现举一例进行说明.

例 某物体以8 m/s2的加速做匀减速直线运动直到停止，求物体停止前的最后一秒内通过的路程.

对本题进行解析，通过题目本身来说，运用正向思维，需先求出最后一秒初的速度，似乎缺少条件，无法求出该题目的解.但如果运用逆向思维来看，把题目看成是由静止做匀加速运动.题目的思路的就变了.即物体在开始做匀加速运动的第一秒所通过的路程和题目中物体做匀减速的停止前的最后一秒所通过的路程是相等的.那么根据公式可得x=at2/2=8×12/2= 4 m.

三、替代思维

不管是在数学，还是在物理中，替代思维的运用非常广.就物理学习中用到的替代思维法引入的物理量就有：质点：用来代替物体使得问题的研究更加简化，重心：为了研究重力可以认为物体各个部分的重力都集中在一个点上，合力与分力的互相替代，使得问题的求解更加方便，很多题目运用常规的思维，解题会非常复杂，而且在计算的过程中容易发生错误，最后导致时间也花费了不少，结果却还是不尽人意.因此，在处理相关类型题目时，要学会将一些物理的变量整合成物理模型，以避免进入到繁琐的解题怪圈之中.把复杂化为简单，这样才能另辟蹊径.对这些题型中的物理量进行等量代换是解决这类题型的关键，可以使整个题目处理起来更为得心应手，从而提高做题效率.这一解题方式在力学、电学及实验数据处理方面运用非常广泛.

例如高中物理中平均速度，平均加速度的引入，就是为了把繁杂的变速运动进行简化，使其可以和匀速运动及匀变速等效.其次，两个物体相撞的问题中，由于其相撞的过程的相互作用力也在不断变化，那在这一研究过程中，就可引入平均力的概念，对其不断变化的过程进行等量代换，简化其复杂的过程.高中物理中等量代换的解题方式随处可见，灵活的运用这一方法，可使物理解题更便捷，更智慧.

例1 物体质量为m,放在水平地面上，与地面之间动摩擦因数为μ，为了使物体沿着水平面匀速运动，需加一个斜向上的拉力，求该拉力的方向与水平面成多大角度时拉力有最小值，最小值是多少？如图4.

图4 图5

常规解法 受力如图，按常规解题思路，列出力的平衡方程最后运用数学方法求出F的最小值.

由Fcosα-μ(mg-Fsinα)=0

得：F=μmg/(cosα+μsinα)

又因为：(cosα+μsinα)

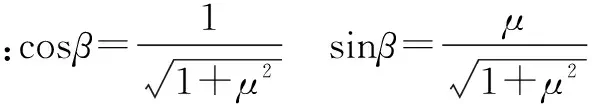
可知：当α=β时(cosα+μsinα)=1，此时F有最小值.

替代解法：此题中，f和N的合力的方向是不变的，设二者的合力方向与竖直方向成β角，既有tanβ=f/N=μ，为一个常数，若用f和N的合力F1替换掉这两个力(图6)，则该题目就可以转化为同一平面内不共线的三力平衡问题(图7)，就可以运用三力平衡中的三角形法中求最值的方法快速得到答案(图8)

图6 图7 图8

从本题的两种解法对比中，不难看出，恰当的运用替代法，可以使问题简化，解题过程更简单，能够赢得时间，减少计算量，提高准确性.

四、估算思维法

估算法是指在研究问题的过程中，忽略次要的因素，只考虑影响所研究问题的主要因素，解题中运用这种方式，可使学生避免受到不必要的干扰，例如在力学中经常忽略空气阻力，忽略物体的形状等，热学中估算固体和液体分子、原子直径时也常会忽略分子原子之间的空隙，运用到这种思维法.

例题1 为了测量井口到水面的距离，让一个小石子从井口自由落下，经过2.5秒后听到石块击水的声音，试估算水面到井口的距离.考虑到声音的传播需要一定时间，估算结果偏大还是偏小(不考虑空气阻力，g=9.8 m/s2v声=340 m/s)

分析 依题意，若不考虑声音的传播所需时间，则2.5秒内石块下落的距离为

H=gt2/2=9.8×2.5μ/2=30.6 m.

若考虑声音传播时间，则石块下落的实际时间少于2.5 s，故上面的深度要大于实际深度.

若考虑声音的传播需要时间，且按v声=340 m/s计算，设井深为H,则有t石+t声=2.5

①

t声=H/v声

②

t石=2.41

③

由上述三式联立，解得H= 28.9 m

两个结果的对比可以看出，忽略声音传播时间计算出的深度与考虑声音传播时间计算出的深度相差不到一米，误差不超过百分之三.但忽略声音传播时间的解题过程要大大简化，大大缩短了运算时间.

本题中石子撞击水面的声音传到井口所需时间跟石子下落的时间相比还是比较小的，对结果的影响也是比较小的，所以在粗略的计算中声音传播所需时间可以忽略不计.类似的处理方法在高中阶段的物理学习中比比皆是，我们可以根据所遇到的问题进行合理的简化处理，以求得快速的解决问题.

良好的解题思维不仅有助于学生在高考物理中获得优异的成绩，同时还可帮助学生拓宽思维方式，有益成长.此外，高中的物理学习，只有正确的培养学生们的解题思维，才可让学生们在高考中达到事倍功半的效果，做到高考中抢占先机，决胜千里.

[1]王永刚.掌握正确思维方法探究物理解题途径[J].科教文汇：下旬刊，2013(1)：168-169.

[2]赵松年.对高中物理解题思维方法的探究与运用[J].教育教学论坛，2013(37)：91-92.

G632

B

1008-0333(2017)01-0066-02