例析动量定理在电磁感应中的运用

福建省惠安第一中学(362100)

陈少杰●

例析动量定理在电磁感应中的运用

福建省惠安第一中学(362100)

陈少杰●

文章通过几例典型变式问题来探讨如何运用动量定理解决电磁学综合应用问题，以培养学生的高中物理应用能力，达到熟练驾驭知识的目的.

高中物理；教学实例；动量定理；电磁感应

在磁场或电磁感应这两章的综合应用中，许多学生有一个非常致命的弱点，那就是不善于用动量定理来处理一些相关问题.

由于电磁感应综合应用中物理量之间的关系比较复杂 ，只从理论上把握上还不够，还必须通过典型问题来培养物理知识应用能力，达到熟练驾驭的目的.下面通过几例变式问题探讨如何运用动量定理解决电磁学综合应用问题.

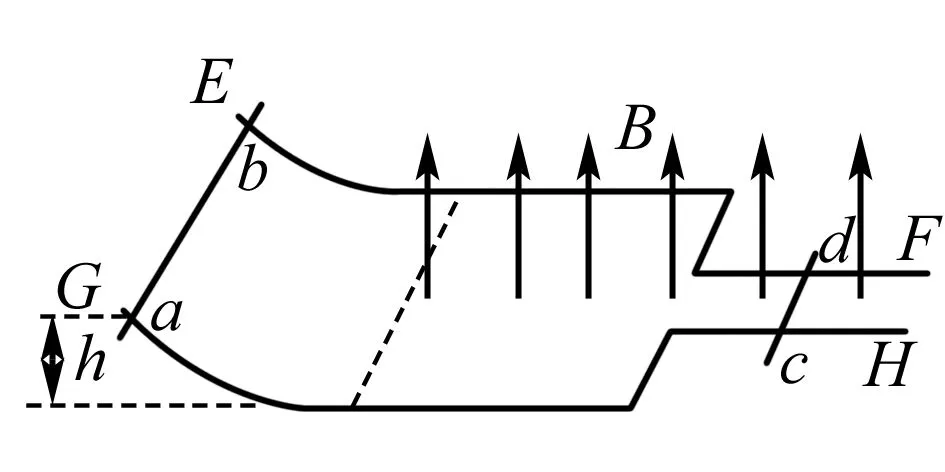
图1

例1 如图1所示，光滑导轨EF、GH等高平行放置，EG间宽度为FH间宽度的3倍，导轨右侧水平且处于竖直向上的匀强磁场中，左侧呈弧形升高.ab、cd是质量均为m的金属棒，现让ab从离水平轨道h高处由静止下滑，设导轨足够长.试求： (1)ab、cd棒的最终速度；(2)全过程中感应电流产生的焦耳热.

解析ab下滑进入磁场后切割磁感线，在abcd电路中产生感应电流，ab、cd各受不同的磁场力作用而分别作变减速、变加速运动，电路中感应电流逐渐减小，当感应电流为零时，ab、cd不再受磁场力作用，各自以不同的速度匀速滑动.

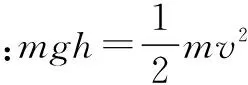
①

由于ab、cd串联在同一电路中，任何时刻通过的电流总相等，金属棒有效长度Lab=3Lcd，故它们的磁场力为：

Fab=3Fcd

②

③

ab、cd受安培力作用，动量均发生变化，由动量定理得：FabΔT=m(v-vab

④

FcdΔT=mvcd

⑤

(2)根据系统的总能量守恒可得：

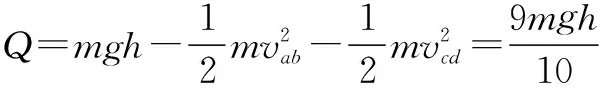
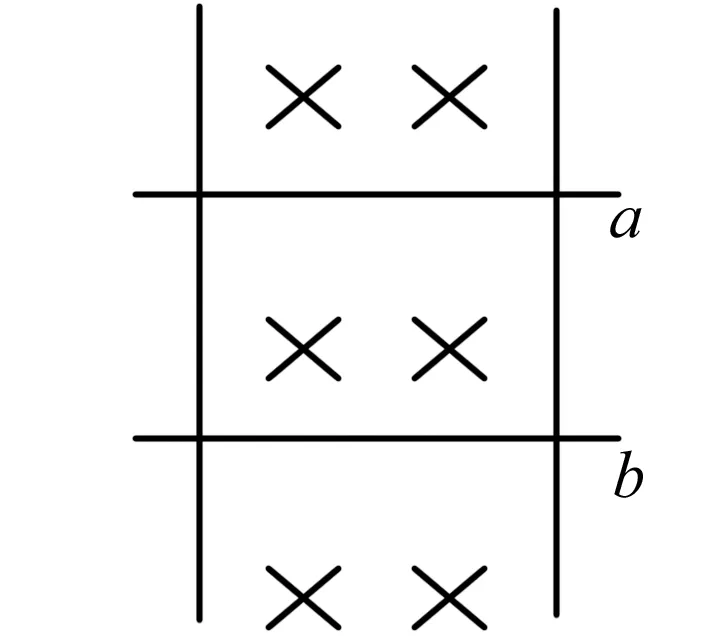
图2

例2 如图2所示，竖直放置的两光滑平行金属导轨，置于垂直于导轨平面向里的匀强磁场中，两根质量相同的导体棒a和b，与导轨紧密接触且可自由滑动.先固定a，释放b，当b的速度达到10 m/s时，再释放a，经过1s后，a的速度达到12 m/s，则(1)此时b的速度大小是多少？(2)若导轨很长，a、b棒最后的运动状态.

解析 (1) 当b棒先向下运动时，在a和b以及导轨所组成的闭合回路中产生感应电流，于是a棒受到向下的安培力，b棒受到向上的安培力，且二者大小相等.释放a棒后，经过时间t，分别以a和b为研究对象，根据动量定理，则有： (mg+F)t=mva(mg-F)t=mvb-mv0

代入数据可解得：vb=18 m/s

(2)在a、b棒向下运动的过程中，a棒产生的加速度a1=g+F/m，b棒产生的加速度a2=g-F/m.当a棒的速度与b棒接近时，闭合回路中的ΔΦ逐渐减小，感应电流也逐渐减小，则安培力也逐渐减小.最后，两棒以共同的速度向下做加速度为g的匀加速运动.

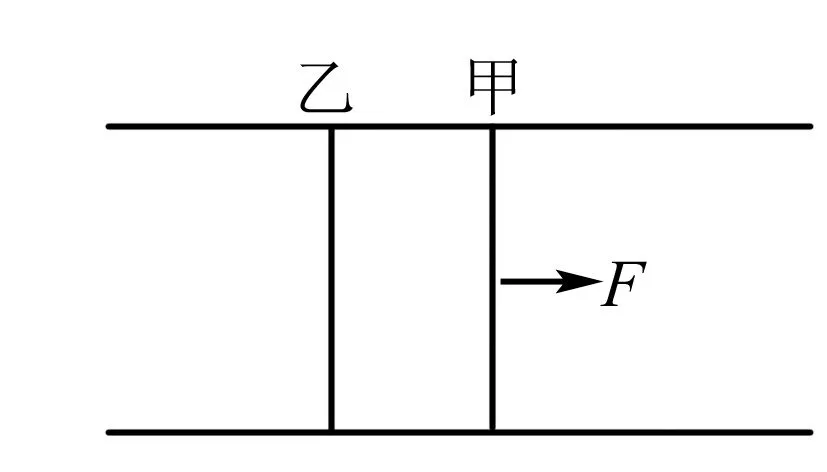
图3

例3 两根平行的金属导轨，固定在同一水平面上如图3所示，磁感强度B=0.5 T的匀强磁场与导轨所在平面垂直，导轨的电阻很小，可忽略不计.导轨间的距离l=0.20 m，两根质量均为m=0.10 kg的平行金属杆甲、乙可在导轨上无摩擦地滑动，滑动过程中与导轨保持垂直，每根金属杆的电阻为R=0.50Ω.在t=0时刻，两杆都处于静止状态.现有一与导轨平行，大小为0.20 N的恒力F作用于金属杆甲上，使金属杆在导轨上滑动.经过T=5.0 s，金属杆甲的加速度为a=1.37 m/s2，求此时两金属杆的速度各为多少？

解析 设任一时刻t两金属杆甲、乙之间的距离为x，速度分别为v1和v2，经过很短时间Δt，杆甲移动距离v1Δt，杆乙移动距离v2Δt，回路面积改变

ΔS=[(x-v2Δt)+v1Δt]l-lx=(v1-v2)lΔt

由法拉第电磁感应定律，回路中的感应电动势：E=BΔS/Δt

回路中的电流：i=E/2R

杆甲的运动方程：F-Bh=ma

由于作用于杆甲和杆乙的安培力总是大小相等、方向相反，所以两杆的动量变化(t=0时为0)等于外力F的冲量：Ft=mv1+mv2

联立以上各式解得v1=1/2[Ft/m+2R(F-ma)/B2l2]

v2=1/2[Ft/m-2R(F-ma)/B2l2]代入数据得v1=8.15 m/s,v2=1.85 m/s.

通过理论与实践的有机结合，加深了对知识的理解，提高了驾驭知识的能力，有效地解决了这个难点.

[1]杨清和.中学物理网络教学中主观题客观化的策略探讨[J].教学月刊(中学版)， 2004(12)：40-45

[2]黄年凤.巧用动量定理解题.数理化学习(高中版)[J]. 2013(7)：31-31

G632

B

1008-0333(2017)01-0065-01