例谈构造法在数学解题中的应用

广东省东源中学(517500)

曾垂乐●

例谈构造法在数学解题中的应用

广东省东源中学(517500)

曾垂乐●

构造法的核心是构造，即通过构造模型、图形实例、中介辅助元素(辅助命题、函数、方程、数列、不等式、向量、特殊曲线等)，以沟通数学的条件与结论间的内在联系而使问题解决.

构造法；数学解题；应用

构造法的突破是创新，即在解题时打破常规，另辟蹊径，表现出简洁、明快、精巧等特点.构造法的思路是从多角度、多渠道引进广泛的联想，等价转化为熟知且有通性通法的新问题.现通过具体实例来谈谈构造法在数学解题中的应用.

一、构造方程

例1 已知x,y,z∈R，且x+y+z=8，x2+y2+z2=24．

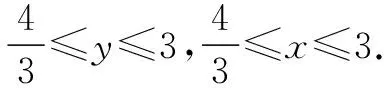
二、构造函数

例2 若实数a、b、c满足a<0，4a-2b+c>0，则有( )

A．b2-4ac=0 B．b2-4ac>0

C．b2-4ac≤0 D．b2-4ac<0

解 令函数f(x)=ax2+bx+c,a<0，其图象为开口向下的抛物线.

由f(-2)=4a-2b+c>0，得函数图象与x轴有两个交点，

所以有Δ=b2-4ac>0.选B.

三、构造基本不等式

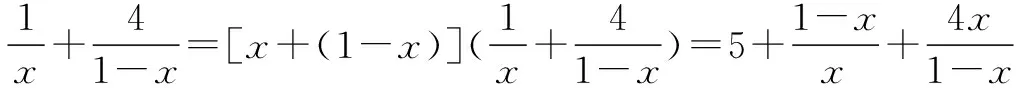
四、构造几何图形

分析 对于这类题目的一般解法是分区间求解，这是比较繁杂的.观察本题条件可构造双曲线，求解更简捷.

∴1-3

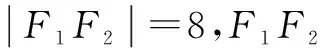
五、构造向量

G632

B

1008-0333(2017)01-0053-01