构造平面几何图形证明代数不等式

江苏省泰州市森南新村15栋103室(225300)

于志洪●

构造平面几何图形证明代数不等式

江苏省泰州市森南新村15栋103室(225300)

于志洪●

本文通过举例，谈谈如何构造平面几何图形证明代数不等式，供初中师生教学时参考.

一、构造等边三角形证明不等式

例1 设x、y、z是介于0与1之间的实数.求证：x(1-z)+y(1-x)+z(1-y)<1.

分析 本题直接证明非常困难，考虑到左边是两个因式乘积之和的形式，而两因式乘积通常与几何中求图形面积的问题有关，因此考虑构造等边三角形或矩形来解.

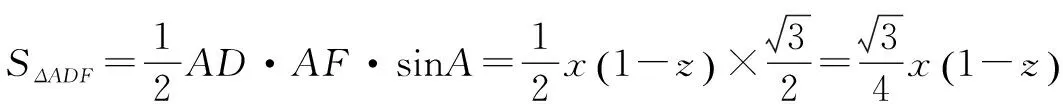
二、构造圆形证明不等式

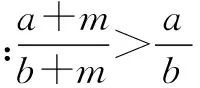
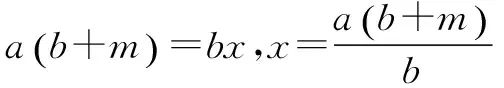
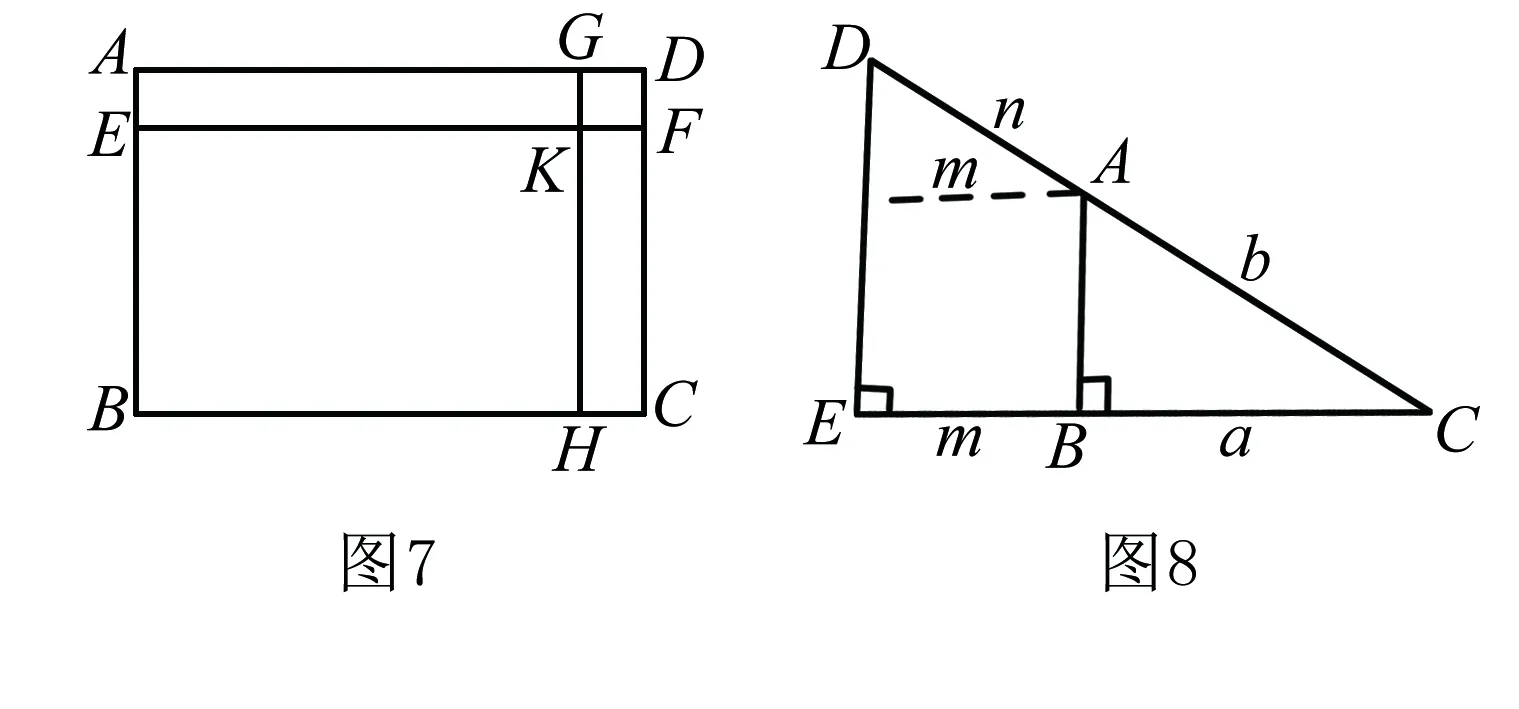
三、构造长方形证明不等式

例3 已知a、b、c、d都是正有理数，求证：

分析 此题初看，似乎无从下手，但仔细观察其整体结构与三角形中三边间关系相似，再观察被开方数结构，容易联想到勾股定理，它们都是直角三角形的斜边，凑在一起就构造出矩形.

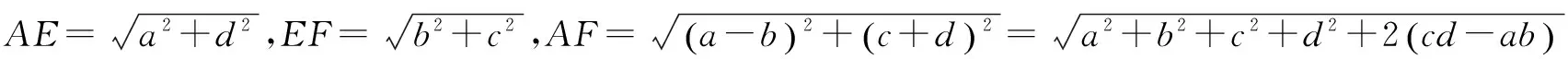
四、构造正方形证明不等式

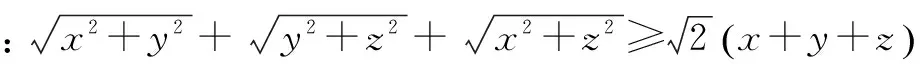
五、构造梯形证明不等式

例5 已知a、b、c、d均为正数，求证：ad+bc.

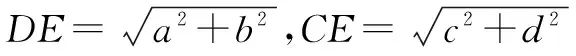
综上所述可知：注意构造几何图形证明代数不等式的专题研究，符合新课程改革关于“让学生的思维活跃起来”的理念要求，有利于提高学生的专题总结水平，有利于学生在研究总结的过程中，拓展视野，启迪思维，有利于学生系统灵活地掌握所学的知识内容，对于帮助学生理解课本内容，培养探索精神和创新意识，提高解题水平和发展思维能力，均颇有益处.

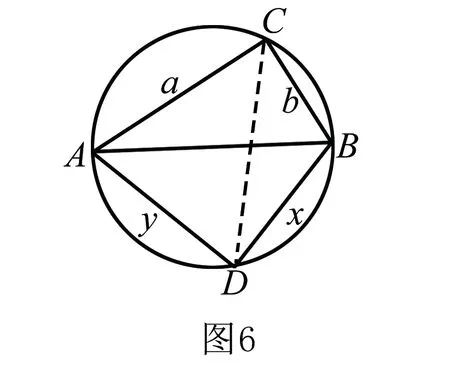
练习 1.已知a，b，x，y均为正实数，且a2+b2=1,x2+y2=1,求证：ax+by≤1.

(提示：构造如图6所示的圆，在直径AB=1的两侧任作Rt△ABC和Rt△ADB,使AC=a,BC=b，BD=x，AD=y.由勾股定理，知a，b，x，y满足题设条件，根据托勒密定理，得AC·BD+BC·AD=AB·CD.因为CD≤AB=1,所以ax+by≤1.)

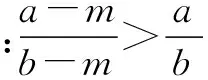
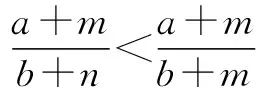
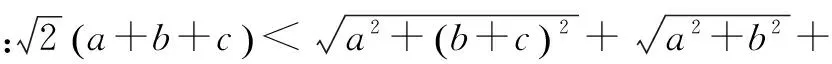
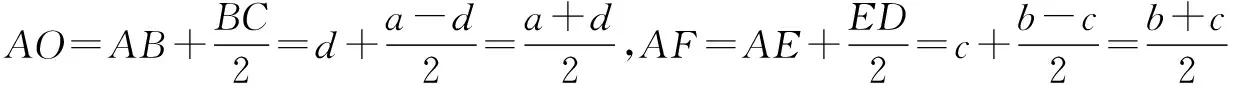
[1]于志洪，吴春胜.构造长方体证明三角不等式[J].数学教学研究，2011(6)

G632

B

1008-0333(2017)01-0019-02